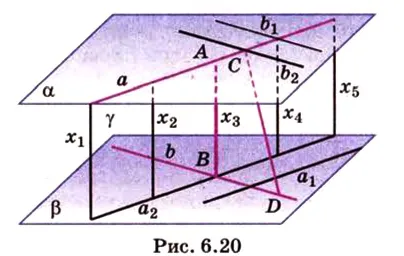
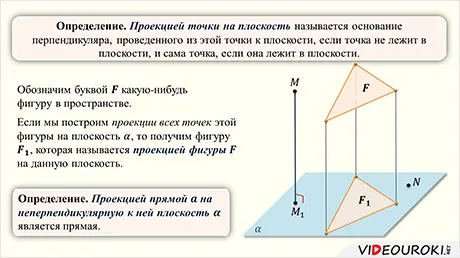
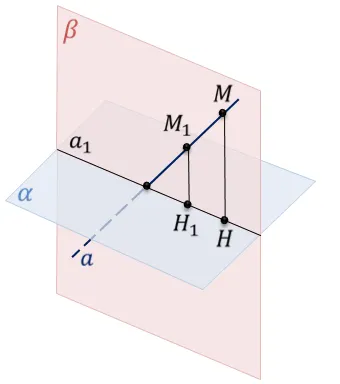
Есть и другой способ найти проекцию, проведя через нее вертикальную линию. к плоскости «, но короче она, скорее всего, не будет. Но если кому-то это нужно, я расскажу алгоритм:
Углы и расстояния в пространстве — определение и вычисление с примерами решения
В планетометрии угол — это геометрическая фигура, образованная двумя лучами, исходящими из точки — вершины угла (лучи — это стороны угла). Это определение угла можно также применить к стереометрии. Углы в пространстве рассматриваются между двумя прямыми, прямой и плоскостью, двумя плоскостями. Давайте опишем и определим каждый из этих элементов.
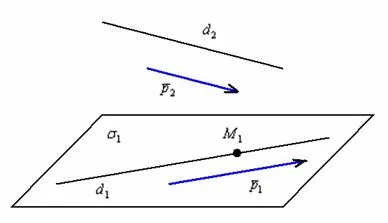
Две прямые, лежащие в одной плоскости, образуют смежные и вертикальные углы в точке их пересечения. В разделе 1 мы повторили все свойства этих углов (прямые углы равны, а смежные углы дополняют друг друга до 180°). В пространстве (аналогично планетометрии) также сохраняются все названия и понятия углов и их величин. Меньший из углов, образованных двумя пересекающимися линиями прямыми, называют углом между прямыми. Угол между перпендикулярными прямыми составляет 90°. Параллельно прямые также образуют угол 0°. В стереометрии угол между скрещивающимися прямыми. Данные углы пересечения прямые
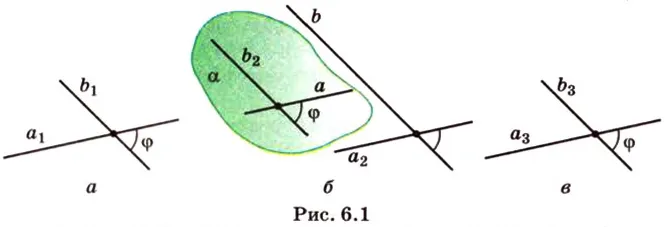
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и параллельны друг другу. и тогда угол между прямыми будет угол между прямыми , где (рис. 6.1,6).
Следовательно, если, то. Перпендикуляры пересекающихся линий прямых мы не говорим, поскольку придерживаемся определения перпендикуляров прямых.
Угол между прямой и плоскостью в пространстве
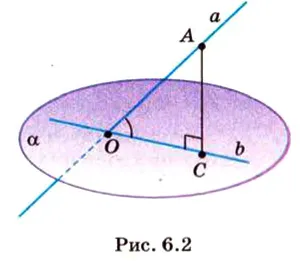
Об угле наклона прямой к плоскости говорится в случае, когда прямая пересекает эту плоскость. Например, для построения угла между прямой мы видим следующие последовательные шаги (рисунок 6.2):
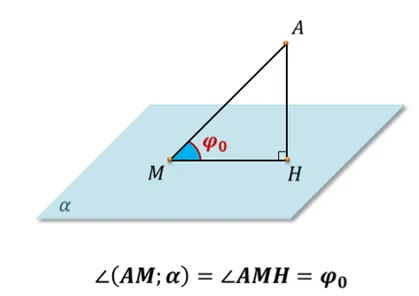
Прямую на плоскость Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая , то угол между ней и плоскостью равен 90°, а если они параллельны, то 0°. Угол между прямой обозначают или и плоскостью
Угол между двумя плоскостями, пространства
Прямая на плоскости делит его на две половиныплоскости. Две полуплоскости могут иметь общую прямую и не образуют единое целое плоскость. В этом случае они образуют форму, называемую двухсторонним углом.
Равносторонний угол — это угол, образованный двумя полудиагональными углами.плоскостями вместе с общей прямой, их ограничивающей. Эту прямую Она называется ребром двугранного угла.
Когда двугранный угол пересекает плоскостью, перпендикулярно его ребру, лучи, с которыми пересекаются данные полууглы, образуют линейный угол, напр.плоскости, образуют линейный угол, например
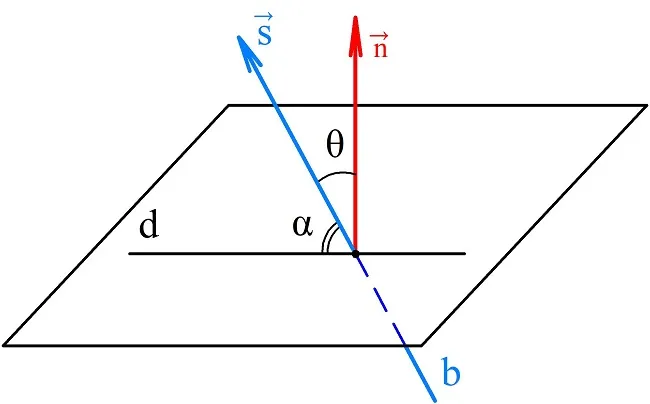
Пересекающиеся плоскости образуют четыре угла. Для определения угла между двумя плоскостями, проводят плоскость, перпендикулярную прямой их пересечения. Пересекается с данным плоскости по двум прямым. Угол между этими прямыми называется углом между данными плоскостями. Т.е. угол между из двух пересекающихся плоскостями — это угол между двумя прямыми, которые принадлежат им плоскостям и перпендикулярны прямой их пересечения. (Рисунок 6.3).
Если линейный угол равен 90 то плоскости они перпендикулярны друг другу. Если плоскости параллельны, тогда угол между ними равен 0°.
Теорема 1
Угол между плоскостями не зависит от положения линейного угла.

Выберите точки (рис. 6.4), которые относятся к следующим пунктам прямой и и и и перпендикулярны друг другу прямой и применить параллельный перенос, перемещающий точку, то прямая , а прямая . Это возможно потому, что прямые они параллельны. Поэтому плоскости совпадают, поэтому линейные углы совпадают и, следовательно, равны. Теорема доказывается следующим образом.
Пример №1
Концы отрезка длиной 24 см лежат на двух перпендикулярах. плоскостям. Расстояния между концами отрезка и линией пересечения заданных плоскостей равны 12 см и
Дано: — отрезок, найдите: углы, проходящие через отрезок и
— проекции точек на плоскости соответственно. Учитывая, что (или, Таким образом, — прямоугэто углы, которые имеют: (по условию). Из ответа. 30°; 45°.
Почему именно это?
В этой задаче Важно построить проекции краев отрезка на другие, перпендикулярные прямые. ей, плоскость. Мы не должны забывать, что они должны быть локализованы на прямой пересечение определенных перпендикуляров плоскостей, в соответствии со свойствами перпендикуляров плоскостей. Кроме того, следует учитывать, что прямоугполных треугольников мы должны правильно использовать определение синуса угла как отношения противоположной ноги к гипотенузе и таблицу значений:
Поэтому треугольники AOB и AOE равны двум пробникам (или согласно первому принципу: две стороны и угол между (т.е. если они равны друг другу и имеют один угол и один угол между ними). В этом случае соответствующие углы также равны: ∠ABO = ∠AEO .
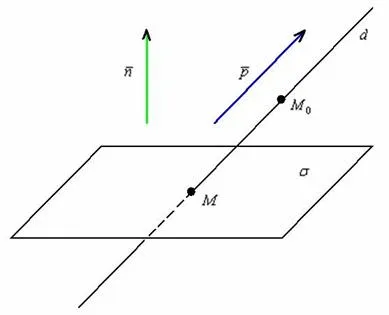
Что есть угол между прямой и плоскостью?
Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.
Вот, смотри: прямая \( a\) плоскость \( \индикатор стиля \Alpha \).
Для определения угла между ними?
В соответствии с определением, которое мы только что дали), нужно опустить перпендикуляр (\( \displaystyle _>\)) из любой точки прямой \( a\) на плоскость \( \индикатор стиля \Alpha \).
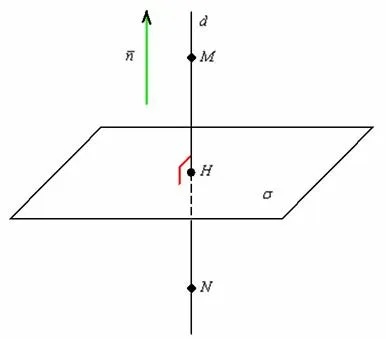
А потом провести прямую через точки \(\displaystyle A\) и \(\displaystyle O\).
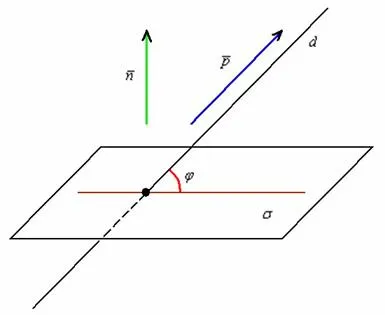
Теперь угол по определению между прямой \( \displaystyle a\) и плоскостью \( \displaystyle \alpha \) равен углу \( \displaystyle \varphi \)) между \( \displaystyle a\) и \( \displaystyle \).
Угол между прямой и плоскостью в задачах
Как найти угол между прямой и плоскостью в задачах?
Как и в других задачах В стереометрии существует два метода определения углов и расстояний: геометрический и алгебраический.
Геометрический метод
Геометрический метод основан на геометрическом методе и алгебраическом методе. найти подходящее место на прямой, бросить вертикальный на плоскость, выяснить, что такое проекция, а затем решить планету задачу найти угол в треугольнике (\(\displaystyle \varphi \)) в треугольнике (часто прямоугольном).
Самая сложная задача — определить, куда падает перпендикуляр и при каком же прямая является проекцией.
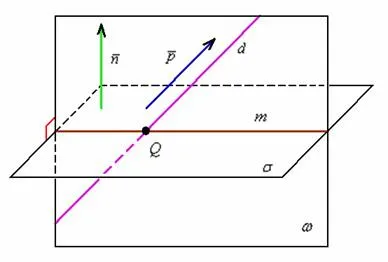
Алгебраический метод
В алгебраическом методе вводим систему координат, определяем координаты двух точек на прямой и уравнение плоскости, а затем формула для вычисления угла между прямой и плоскостью.
Здесь (\( \displaystyle _>,_>,_>\)), (\( \displaystyle _>,_>,_>\))) — Координаты двух точек на прямой, \( \displaystyle A\), \( \displaystyle B\), \( \displaystyle C\) — это координаты в уравнении плоскости\( \displaystyle Ax+By+Cz+D=0\).
Самое сложное — хорошо запомнить формулу и понять, откуда берутся все буквы.
Теперь мы будем работать над одним. задачу, где нужно найти угол между прямой и плоскостью двумя различными способами: геометрически и алгебраически.
Задача по поиску угла между прямой и плоскостью
В правильной шестиугольной пирамиде \( \displaystyle SABCDEF\) точка \( \displaystyle M\) является центром ребра.
Найти угол между прямой Точка \( \displaystyle FM\) и плоскостью является основой, если \( \displaystyle SE=3FE\).
Решение задачи геометрическим методом
Поскольку в правильной пирамиде высота наклоняется к центру основания \( \displaystyle O\), \( \displaystyle OE\) является проекцией \( \displaystyle SE\), а точка \( \displaystyle M\) проецируется на \( \displaystyle K\) — центр отрезка \( \displaystyle OE\).
Теперь \( \displaystyle FK\) является проекцией \( \displaystyle FM\) и искомый угол равен между прямой Точка \( \displaystyle FM\) и плоскостью основания составляет \( \displaystyle \угол MFK\).
Я ищу эту перспективу. Предположим, что стороны основания равны \( \displaystyle a\), тогда боковые грани равны \( \displaystyle 3a\). Обратите внимание, что \( \displaystyle \Delta MFK\) – прямоуги в этом треугольнике нам нужно найти острый угол.
Проще всего найти тангенс этого угла.
Открыть ответы…
Чтобы открыть все задачи Руководство, покрытое синими баннерами (как этот), пишите один раз:
Решение задачи алгебраическим методом (методом координат)
Введем систему координат, центрированную на \( \displaystyle O\), \( \displaystyle Ox\) — вдоль \( \displaystyle OE\), \( \displaystyle Oy -\bot AF\) и \( \displaystyle CD\), \( \displaystyle Oz\) — вдоль \( \displaystyle OS\).
Тогда координаты точки \( \displaystyle F(\frac,~-\frac>;0)\)
Координаты точки \( \displaystyle M\):
Уравнение плоскости \( \displaystyle ABCDEF:Z=0\)
Поэтому применяется формула для расчета угла. между прямой и плоскостью:
Открыть ответы…
Мы постоянно работаем над улучшением этого учебника, и вы можете нам помочь. Получите доступ к учебнику Юклавы и пользуйтесь им без ограничений (100+ статей по всем темам ЕГЭ и ОГЭ, 2000+ разобранных задач, 20+ вебинаров-семинаров)
Все зависит от задачи. Поэтому важно научиться использовать оба метода.








