Не бойтесь браться за неизвестные проекты. Ковчег был построен любителями, «Титаник» — специалистами. Пустые карманы никогда не помешают нам стать теми, кем мы хотим быть. Только пустая голова и пустое сердце могут предотвратить это.
Как упростить алгебраическое выражение
Некоторые алгебраические примеры могут привести учеников в ужас от одного их вида. Большие представления не только пугают, но и сильно затрудняют вычисления. Попытка понять, что за этим последует, может сбить вас с толку. Вот почему математики всегда стараются максимально упростить «страшную» задачу, а затем решают ее. Как ни странно, такие уловки значительно ускоряют процесс.
Упрощение — один из фундаментальных принципов алгебры. Вы можете обойтись без него при решении простых задач, но вам может быть трудно вычислять примеры. Вот где пригодятся ваши навыки! Тем более, что для этого не требуется сложных математических знаний. Достаточно выучить и отработать несколько основных приемов и типов.
Необходимые знания и умения
При решении уравнений важно соблюдать правильную последовательность действий с числами, какими бы сложными ни были вычисления.
- скобки;
- возведение в степень;
- умножение;
- деление;
- сложение;
- вычитание.
Последние два пункта можно смело поменять местами, и это совершенно не повлияет на результат. Однако сложение двух соседних чисел строго запрещено, если рядом с одним из них стоит символ умножения! Ответ, если и есть, то неправильный. Поэтому последовательность должна быть запомнена.
Применение подобных
К таким элементам относятся числа с переменными одного класса или одного разряда. Существуют также очень сокращенные и свободные термины, рядом с которыми нет букв, обозначающих неизвестные.
Идея заключается в том, что если скобки отсутствуют, то выражение может быть упрощено путем аналогичных добавлений или удалений.
- 8x 2 и 3x 2 — оба числа имеют одну и ту же переменную второго порядка, поэтому они подобны и при сложении упрощаются до (8+3)x 2 =11x 2, тогда как при вычитании получается (8-3)x 2 =5x 2 ;
- 4x 3 и 6x — а тут «х» имеет разную степень;
- 2y 7 и 33x 7 — содержат различные переменные, поэтому, как и в предыдущем случае, не относятся к подобным.
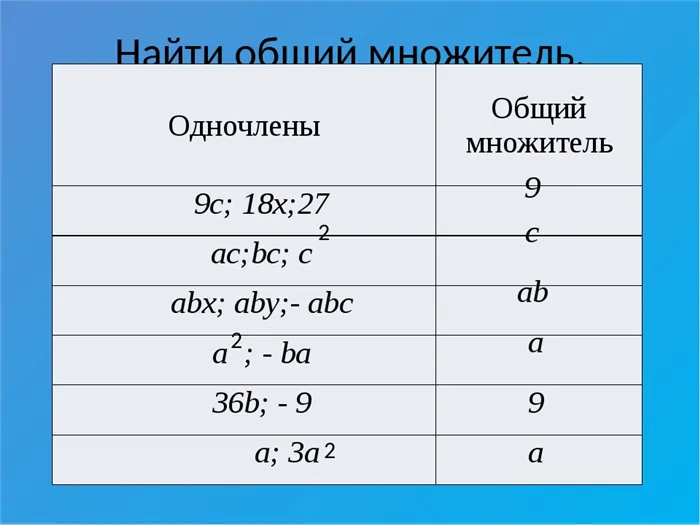
Разложение числа на множители
Этот маленький математический трюк, если научиться им правильно пользоваться, может помочь вам в будущем не раз справиться с трудными проблемами. Кроме того, легко понять, как работает «система». Разложение — это произведение различных элементов, которое при вычислении дает исходную величину. Таким образом, 20 можно выразить как 20 x 1, 2 x 10, 5 x 4, 2 x 5 x 2 и т.д.
Предсказание: множитель всегда равен делителю. Поэтому для деления числа нужно искать такую пару операций, при которой исходное число делится без остатка.
Это можно сделать с помощью свободных условий или чисел, используя переменные. Главное — не потерять последнего в расчете. Даже после расширения неизвестное не может «уйти в никуда» вместе с ним. Он остается в одном из множителей.
Первое число, которое может делиться только на один или на единицу, не анализируется — оно не имеет смысла.

Основные способы упрощения
Первое, что бросается в глаза, это следующее
Алгебраические примеры в школьных материалах часто основаны на предположении, что их можно красиво упростить.
Вычисления в скобках
Обратите внимание на знак перед опорой! Распространение или разделение применяется к каждому элементу внутри, а минус меняет существующий символ ‘+’ или ‘-‘ на противоположный.
Скобки вычисляются по убыванию типа правила или распространения, а затем применяется то же самое.
Сокращение дробей
Сокращение дробей не является сложной задачей. Сокращать дроби также легко, и легко «убегать» от субдоменов по одному по мере их добавления. Однако пример можно упростить и до этого. Обратите внимание на числитель и знаменатель. Часто они содержат явную или неявную информацию, которая может взаимно усиливать друг друга. Однако в первом случае достаточно просто удалить лишние части, а во втором — хорошо подумать и свести части уравнения к упрощенной форме. Использованные методы:.
- поиск и вынесение за скобки наибольшего общего делителя у числителя и знаменателя;
- деление каждого верхнего элемента на знаменатель.
Если выражение или часть выражения находится под корнем, то основная задача упрощения во многом такая же, как и для дробей. Вам нужно найти способ полностью избавиться от него. Если это невозможно, сведите к минимуму признаки, мешающие расчету. Например, знак √(3) или √(7).
Хороший способ упростить подравенство — попытаться разбить его на коэффициенты. Некоторые из факторов можно вычесть из уравнения. Очевидный пример: √(90) = √(9 x 10) = √(9) x √(10) = 3√(10).
Другие маленькие хитрости и сложности:.
- эту операцию упрощения можно проводить с дробями, вынося её за знак как целиком, так и отдельно числитель или знаменатель;
- раскладывать и выносить за пределы корня часть суммы или разности нельзя ;
- при работе с переменными обязательно учитывайте её степень, она должна быть равной или кратной корню для возможности вынесения: √(x 2 y)=x√(y), √(x 3 )=√(x 2 ×x)=x√(x);
- иногда допускается избавление от подкоренной переменной путём возведения её в дробную степень: √(y 3 )=y 3/2 .

Упрощение степенного выражения
Для простых вычислений с использованием минуса или плюса, а как насчет умножения или деления переменных с разной силой, если пример упрощен путем добавления аналогичных примеров? Это можно легко упростить, если запомнить два важных момента.
- Если между переменными стоит знак умножения — степени складываются.
- Когда они делятся друг на друга — из степени числителя вычитается она же знаменателя.
Единственным условием такого упрощения является то, что оба члена имеют одинаковый базис. Для наглядности пример:.
- 5x 2 ×4x 7 +(y 13 /y 11 )=(5×4)x 2+7 +y 13- 11 =20x 9 +y 2 ;
- 2z 3 +z×z 2 -(3×z 8 /z 5 )=2z 3 +z 1+2 -(3×z 8-5 )=2z 3 +z 3 -3z 3 =3z 3 -3z 3 =0.
Обратите внимание, что операции с числами перед переменными выполняются по обычным математическим правилам. Если вы внимательно посмотрите, то увидите, что силовые элементы уравнения «работают» одинаково.
Первоначально мы получили выражение -1 (3 + (-5) + (-11)), но раскрыв скобки, мы получили выражение — (3-5-11). Открывающие скобки — это тема следующего урока, поэтому, если у вас возникли трудности с этим примером, можете пока его пропустить.
Вынесение общего множителя за скобки

В начале урока на примере покажите, как вычесть общий множитель из скобок. Это позволяет анализировать полином, заданный множителем. Далее в уроке вы узнаете, как убрать общие множители из скобок. Также будет показано, как вычитание общих множителей может помочь в решении уравнений и некоторых задач.
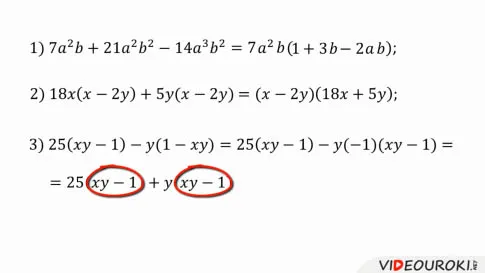
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам из набора, необходимо приобрести их в каталоге и добавить в личный кабинет.


Конспект урока «Вынесение общего множителя за скобки»
-Применяет правила размещения общего множителя за скобкой.
-Подробнее рассмотрим пример вынесения общего множителя за скобку.
Рассмотрим многочлен: — Многочлен — это мультипликативное уравнение.
Обратите внимание, что каждый из его членов может быть выражен как произведение двух множителей.
Используя распределительный закон, полученное выражение можно выразить как произведение двух множителей.
Поэтому мы выразили полином как произведение двух множителей. Другими словами, мы проанализировали его как мультипликатор.
Этот метод разложения многочлена на множители называется удалением общего множителя из скобок.
Преобразования тождеств регулярно встречаются в алгебре 5, 6 и 7 классов. В этой статье снова упоминается распределительный закон, на котором основано правило вынесения общего множителя за скобки.
Вынесение общего множителя за скобки
Отметим, что в соответствии с Федеральным законом N273-ФЗ «Об образовании в Российской Федерации» об организации образовательной деятельности обучение и воспитание обучающихся с ограниченными возможностями здоровья организуется совместно с другими обучающимися либо в отдельных классах или группах.


Курсы обучения на рабочем месте
Авторская разработка онлайн-курса

Курсы обучения на рабочем месте
Современные педтехнологии в деятельности учителя

Курсы обучения на рабочем месте
Педагогические и психологические аспекты подготовки школьников к сдаче ГИА

«Формирование единой системы гармоничного и эффективного развития математических способностей детей»
Рабочие листы и ресурсы для учителей и преподавателей
Более 2500 образовательных ресурсов для школ и дома.
Описание презентации по отдельным слайдам:

Тема урока: «Вынесение общих множителей за скобки». Гудкова Татьяна Валерьевна. преподаватель математики мбоу сош № 27 г. Брянска.

15 января 2014 года, в 18-00, город Брянск встречает XXII Олимпийский огонь!

Домашнее задание №628 (a) a (b -c) + b (c -a) + c (a -b) = ab -ac + bc -ba + ca -cb = 0 #636 (a) 3x + 5 _ x+1 5 3 3 3 (3x+5) — 5 (x+1) = 15 9x+15-5x -5 = 15 4x = -15 4x = 5 x = 1,5 Ответ: h = 1, 5 2 2 2 2 2 2 2. 2 2 = 1 Нет. 631 (в, г) в) 5х (12х-7) — 4х (15х-11) = 30+29х 60х -35х-60х+44х = 30+29х 9х-29х = 30 -20х = 30 х = 30 🙁 -20) х = -1,5 Ответ: х = -1. г) 24х- 6х (13х-9) = -13-13x (6x-1) 24x-78x +54x = -13-78x +13x 78x-78x +78x -13x = -13 65x = -13 x = -13 : 68 x = -0,2 Ответ.

Нет. 643 называли 60 га ежедневно вместо 50 га, цех мог сократить пастбища на один день быстрее, чем планировалось. Какова площадь пастбища? Решение: x (e) Тогда план должен быть: (x -1) (e) отработан, 50x (га) — площадь пастбища по проекту 60 (x -1) (га). 60 га усталости в день. 50x = 60 (x -1) 50x -60x = -60 -10x = -60 x = 6 d) при условии. 6*50 = 300 (га) — площадь пастбищ. Ответ: 300 га. ; пастбище согласно плану HA 50 в день. x 50x было 60? x- 1 меньше единицы 60 (x -1)

Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 914 006
‘Интеграция современного искусства в детское творчество’
Сертификат и скидка для каждого участника.
‘Ищу учителей для участия в группе «Infowalk»‘
Другие материалы
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
- Тема: § 43. Свойства логарифмов
‘Практический подход к решению проблемы потери смысла жизни: логопедия’.
Сертификат и скидка для каждого участника.
Вам будут интересны эти курсы:
- Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
- Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
- Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
- Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
- Курс профессиональной переподготовки «Организация логистической деятельности на транспорте»
- Курс повышения квалификации «Маркетинг в организации как средство привлечения новых клиентов»
- Курс повышения квалификации «Экономика: инструменты контроллинга»
- Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
- Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
- Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
- Курс повышения квалификации «Актуальные вопросы банковской деятельности»
- Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
- Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»
Оставьте свой комментарий
Данный материал опубликован Татьяной Гудковой. Инфоурок — это информационный посредник, предлагающий пользователям возможность публиковать на сайте методические материалы. Пользователи, загружающие материалы на сайт, несут полную ответственность за них и содержащуюся в них информацию, а также за соблюдение авторских прав.
Если вы считаете, что материал нарушает авторские права или должен быть удален с сайта по любой другой причине, вы можете подать жалобу на материал.
Автор материала
- На сайте: 4 года и 9 месяцев
- Подписчики: 0
- Всего просмотров: 27804
- Всего материалов: 15
Московский институт профессиональной подготовки и повышения квалификации преподавателей
Множители символов не всегда могут быть удалены из скобки. Общие множители могут состоять только из цифр, так как для буквенной части выражения ничего подходящего нет.
Вынесение общего множителя за скобки в буквенном выражении
Гораздо интереснее исчерпать общие факторы из скобок с алфавитными выражениями.
Давайте сначала рассмотрим простой пример. Предположим, у нас есть выражение 3 a + 2 a. Снимите общий коэффициент с кронштейна.
Общий фактор виден невооруженным глазом, т.е. он находится в факторе a. Снимите его с кронштейна. Для этого запишите сам множитель A, а затем рядом со скобкой напишите выражение 3 a + 2 a, но без множителя, так как он заключен в скобки.
![]()
Как и в случае с числовым выражением, разделите каждую сумму на коэффициент депривации. Это выглядит следующим образом:.

В обеих фракциях переменная A уменьшена на a. Напротив, числитель и знаменатель содержат единицы. Причина получения единиц заключается в том, что любое число может заменить его. Эта переменная была как в числителе, так и в знаменателе. Если числитель и знаменатель имеют одинаковые числа, то наибольшим общим делителем является само число.
Например, если A заменить на число 4, то структура станет такой Тогда обе дроби можно уменьшить на четыре.

Результат тот же, что и в предыдущем случае, а не в четыре раза больше.
Поэтому не пугайтесь, когда на экране появляются различные аббревиатуры. Переменные являются полными множителями, даже если они представлены буквами. Такие множители можно заключать в скобки, сокращать и выполнять любым другим способом, разрешенным для обычных чисел.
Символьные выражения содержат буквы (переменные), а также числа. Поэтому обычным коэффициентом, выведенным за скобки, является знаковый коэффициент, который часто состоит из числа и буквы (quotient и variable). Например, следующее уравнение представляет собой множитель символов.
Прежде чем выносить такой множитель за скобку, необходимо определить, какие числа входят в числовую часть общего множителя, а какие — в буквенную. Другими словами, вам нужно знать, какие коэффициенты имеет общий множитель и какие переменные он содержит.
Рассмотрим уравнение 10 a + 15 a. Попробуйте убрать общий множитель из скобок. Во-первых, определите, из чего состоит общий множитель, т.е. какие коэффициенты найдены и какие переменные включены.
Коэффициент общего множителя должен быть наибольшим общим делителем степени выражения буквенного выражения 10 a + 15 A. Коэффициенты выражения равны 10 и 15, а их наибольший общий делитель равен 5. Следовательно, 5 — это коэффициент общего множителя, который выносится за скобки.
Теперь нам нужно определить, какие переменные входят в общий множитель. Для этого рассмотрите уравнение 10 A + 15 A и найдите буквенный коэффициент, входящий во все члены. В данном случае это фактор А. Этот коэффициент включен в каждое из условий 10 A + 15 A. Таким образом, A — это буквенная часть общего коэффициента, которая выносится за скобку.
Это можно сделать с помощью свободных условий или чисел, используя переменные. Главное — не потерять последнего в расчете. Даже после расширения неизвестное не может «уйти в никуда» вместе с ним. Он остается в одном из множителей.









