Если окружность также касается сторон компакт-диска, он пережигается в четырехугольник. В противном случае компакт-диск является вторичным или не имеет ничего общего с циклом. Создадим линию, параллельную ей.
Окружность, вписанная в треугольник. Теоремы и их рассмотрение
Наука об измерении объема, площади и других величин зародилась еще в Древнем Египте. Это было вызвано строительством пирамид. Это потребовало довольно сложных расчетов. И помимо строительства, важно было правильно измерить грунт. Таким образом, наука геометрия от греческого «геос» (земля и «метрио») считает.
Изучению геометрических фигур способствовало наблюдение за астрономическими явлениями. И уже в 17 веке до н.э. нашел свой метод вычисления площади круга, объема сферы и, самое главное, открытие теоремы Пифагора.
Формулировка теоремы для окружности, вписанной в треугольник, выглядит следующим образом
В треугольник может быть вписана только одна окружность.
При таком расположении круг является вписанным, а треугольник — периметром.
Формулировка теоремы о центре окружности, вписанной в треугольник, такова
Центральная точка окружности, вписанной в треугольник, является точкой пересечения биссектрис этого треугольника.
Окружность, вписанная в равнобедренный треугольник
Окружность вписана в треугольник, если хотя бы одна точка является касательной ко всем его сторонам.
На рисунке ниже изображена окружность, вписанная в равнобедренный треугольник. Условия теоремы для окружности, вписанной в треугольник, выполнены. То есть, она является касательной ко всем сторонам треугольников AB, BG и CA в точках R, S и Q соответственно.
Одним из свойств равнобедренного треугольника является то, что контур крайнего значения касается основания треугольника (BS = SC), а радиус круга крайнего значения равен одной трети высоты треугольника (SP = AS / 3).
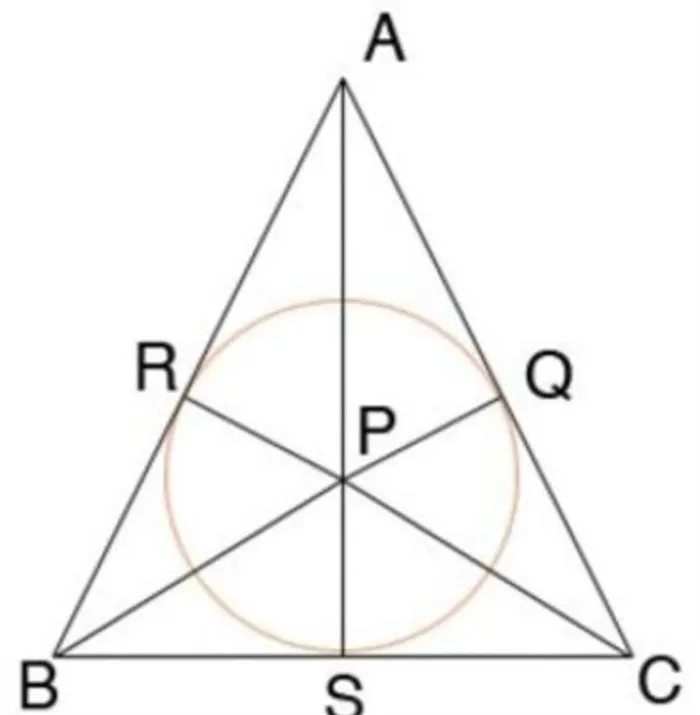
Свойства теоремы об окружности, вписанной в треугольник:.
- Отрезки, выходящие из одной вершины треугольника к точкам касания с окружностью, равны. На рисунке AR = AQ, BR = BS, CS = CQ.
- Радиус окружности (вписанной) — это площадь, деленная на полупериметр треугольника. Как пример, нужно начертить равнобедренный треугольник с теми же буквенными обозначениями, что на картинке, следующих размеров: основание ВС = 3 см, высота AS = 2 см, стороны АВ=ВС, соответственно, получаются по 2,5 см каждая. Проведем из каждого угла биссектрису и место их пересечения обозначим как Р. Впишем окружность с радиусом PS, длину которого нужно найти. Узнать площадь треугольника можно, умножив 1/2 основания на высоту: S = 1/2 * DC * AS = 1/2 * 3 * 2 = 3 см2. Полупериметр треугольника равен 1/2 суммы всех сторон: Р = (АВ + ВС + СА) / 2 = (2,5 + 3 + 2,5) / 2 = 4 см; PS = S/P = 3/4 = 0,75 см2, что полностью соответствует действительности, если измерить линейкой. Соответственно, верно свойство теоремы об окружности, вписанной в треугольник.
Окружность, вписанная в прямоугольный треугольник
Для прямоугольных треугольников применимы свойства теоремы об окружности, вписанной в треугольник. Кроме того, он добавляет возможность решать задачи, связанные с аксиомами теоремы Пифагора.
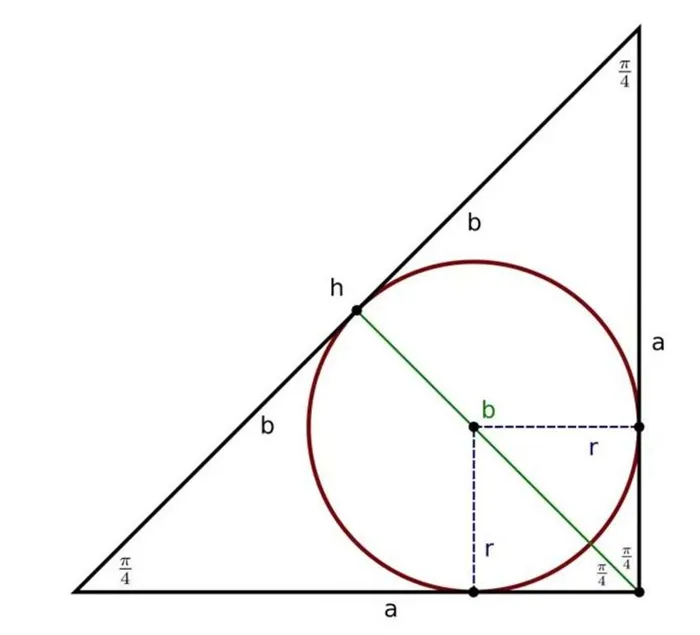
Радиус окружности, вписанной в прямоугольный треугольник, можно определить следующим образом Сложите длины перпендикулярных линий, вычтите значение гипотенузы и разделите полученное значение на два.
Существует хорошая формула для вычисления площади треугольника — умножьте периметр на радиус вписанной в треугольник окружности.
Сложный многоугольник, вписанный в выпуклый многоугольник, представляет собой окружность, проходящую через все стороны многоугольника, причем каждая сторона является касательной к целочисленному контуру.
В четырёхугольнике
Вписанный четырехугольник должен быть выпуклым, если он не имеет независимых сечений («простой»).
В выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны:
В каждом из описанных четырехугольников середина диагонали и центр внутренней окружности лежат на одной прямой (теорема Ньютона). Она также является центром сечения с пересечением на противоположной стороне четырехугольника. Эта линия называется линией Гаусса. Центр окружности, вписанной в четырехугольник, является пересечением высоты треугольника с пересечением диагоналей и вершинами противоположного пересечения (теорема Брокара).
В сферическом треугольнике
Вписанная окружность сферического треугольника — это окружность, касательная ко всем его сторонам.
- Тангенс радиуса 1 вписанной в сферический треугольник окружности равен 2 :73-74
- Вписанная в сферический треугольник окружность принадлежит сфере. Радиус, проведенный из центра сферы через центр вписанной окружности пересечет сферу в точке пересечения биссектрис углов (дуг больших кругов сферы, делящих углы пополам) сферического треугольника 2 :20-21 .
См. также
- ↑ Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведенного из центра сферы через центр окружности, со сферой и точку касания окружностью стороны треугольника.
- ↑ 1 2 Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М .: Просвещение, 1991. — С. 89. — 383 с. — ISBN 5-09-001287-3
- Понарин Я. П. Элементарная геометрия. В 2 тт. — М .: МЦНМО, 2004. — С. 52-53. — ISBN 5-94057-170-0
Фонд Викимедиа. 2010.
Полезное
Смотреть что такое «Вписанная окружность» в других словарях:
Круг — и его центральная окружность — это геометрическое место всех точек на плоскости, которые равноудалены от определенной точки, называемой центром, на определенное неотрицательное расстояние, называемое радиусом. Содержание … Википедия.
Регистрационный круг — Эндкин (включая центр I) и 3 экскола.
Циркуль — это многоугольный круг, содержащий все вершины многоугольника. Центр — это точка (взятая … Википедия.
Смежный цикл — цикл наименьшего диаметра, описанный вокруг цикла наибольшего диаметра, зафиксированного в фактическом профиле внешней поверхности оборота или фактическом профиле внутренней поверхности оборота. … … … Обратите внимание, что если должность технического переводчика руководства
Пирибола — окружность круга, а центр — геометрическое положение точки на уровне, равном определенной точке, называемой его центром. В словаре есть статья ‘круг’ регистрационный круг Аполлоний регистрационный круг.
Полукруг — окружность и центр окружности — это геометрическое положение точки на уровне, равном определенной точке, называемой ее центром. В Викисловаре есть статья ‘Круг’ круг регистрации круг регистрации круг регистрации круг регистрации круг регистрации круг регистрации единый круг Аполлония … … Википедия.
Строка окружности — окружность круга и его центр — это геометрическое положение точки на уровне, равном определенной точке, называемой его центром. В Викисловаре есть статья ‘Круг’ Регистрационный круг Регистрационный круг Регистрационный круг Регистрационный круг Единый круг Аполлония … … Википедия.
Центральный угол — окружность окружности и центр окружности — геометрическое положение точки на плоскости, равное определенной точке, называемой ее центром. В словаре запись «круг» — зарегистрированный круг Зарегистрированный круг 1 зарегистрированный круг Круг Аполлония — единичный круг … … Википедия.
Треугольник — в этом термине есть и другие понятия. См. треугольник (понятие). Треугольник (евклидово пространство) — это геометрическая фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой. Три очка … … Википедия.
Зарегистрированные и обозначенные фигуры — основы геометрии. Многоугольник называется зарегистрированным на кривой, очерченной вокруг выпуклой кривой, и многоугольником, если все вершины многоугольника лежат на кривой (рис. 1). Многоугольники называются периметром кривых, а кривые — … … Большая советская энциклопедия.
В качестве доказательства рассмотрим треугольник ABC. Постройте мезосайты на сторонах этого треугольника. Точка пересечения этих линий совпадает с центром окружности. Соедините эту точку с точками A, B и C.
Описанная окружность
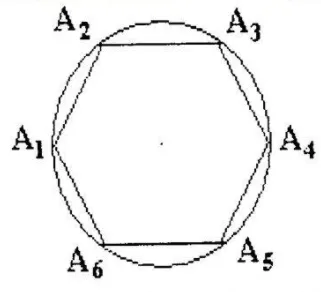
Если все вершины многоугольника лежат на окружности, то окружность называется периметром многоугольника (рис. 3).
Многоугольник, удовлетворяющий условиям определения 2, называется окружностью.
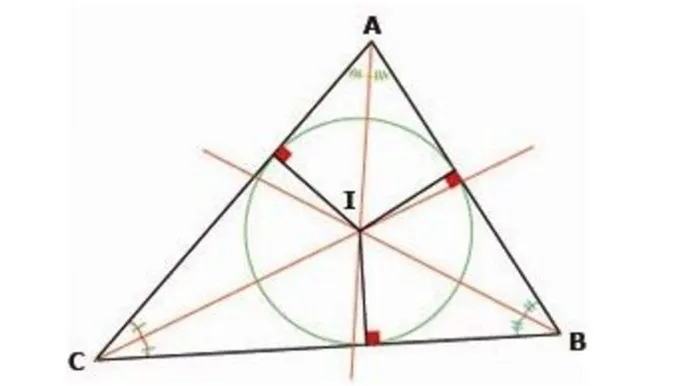
Рисунок 3: Периметр граничной цепи
Теорема 2 (об окружности, описанной около треугольника)
Любой цикл может быть описан вокруг любого треугольника, и только один может быть описан.
Доказательство.
Рассмотрим треугольник $ ABC $. Нарисуйте середину преступника, пересекающую $ o $ и соединяющую эту точку с вершиной треугольника (рис. 4).

Рисунок 4: визуализация теоремы 2.
Существование: постройте окружность в центре луча $ o $ o и $ oc. Точка $ o находится от вершины треугольника. То есть, $ oa = ob = oc $. В результате построенная окружность проходит через все вершины треугольника и поэтому описана вокруг треугольника.
Единственность: предположим, что вокруг треугольника $ abc $ может быть описан другой $ o ‘$-центр. Поскольку его центр находится в вершине треугольника, он совпадает с точкой $ o и имеет радиус, равный $ oc.$ Этот цикл совпадает с первым циклом.
Теорема доказана.
Поиск 1: Центры окружности совпадают с точками пересечения ее середин.
Ниже приведены некоторые элементы, связанные с концепцией цикла.
Не всегда можно описать окружность вокруг четырехугольника.
Для каждого зарегистрированного четырехугольника сумма противоположных углов равна $^0 $.
Если сумма противоположных углов четырехугольника равна $^0 $, то вокруг него можно описать окружность.
Пример задачи на понятия вписанной и описанной окружности
В равнобедренном треугольнике основание равно 8 см, а боковые стороны — 5 см. Найдите радиус в клетке.
Рассмотрим треугольник $ ABC $. Из вывода 1 мы знаем, что центр в клетке находится на пересечении биссектрис. Пересечение балок $ ak $ bm и $ bm в точке $ o $. Проведите перпендикуляр $ oh $ из $ o $ o $ к стороне $ bc $. Рисунок рисунка:.
Поскольку треугольник равнобедренный, $ bm $ является и медианой, и высотой. По теореме Пифагора, $ 2 =^2-^2, Lo_ bm = \ sqrt<^2-\frac^2>> = \ sqrt = \ sqrt = $ 3. $ om = oh = r $ — радиус регистрационного цикла. Так как $ mc $ и $ ch $ являются пересекающимися касательными отрезками, по теореме о пересечении касательных существует $ ch = mc = 4 \ см $. Следовательно, $ bh = 5-4 = 1 \ см $. $ bo = 3-r $. Из треугольника $ ohb $ по теореме Пифагора получаем
Окружность называется зарегистрированной под углом, если она лежит на углу и касается стороны. Центр окружности, зарегистрированной под углом, лежит на биссектрисе этого угла.
Вписанный и описанный четырехугольники
Не все четырехугольники могут иметь цикл регистрации. Например, круг не может быть зарегистрирован в прямоугольнике. На плане видно, что окружность касается только трех своих сторон, что не соответствует определению.
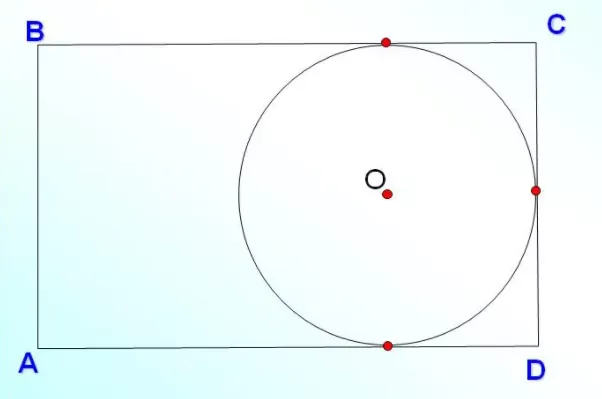
Допущения для окружности, зарегистрированной на четырехугольнике
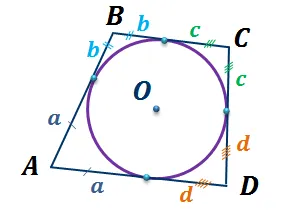
Окружность вписана в четырехугольник, если сумма длин противоположных сторон равна.
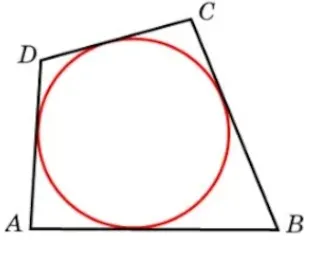
На рисунке это условие выполняется, т.е. ad + bc = dc + ab
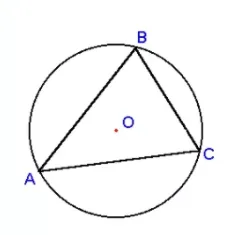
Если сумма противоположных углов равна 180 градусам, то окружность является четырехугольной.
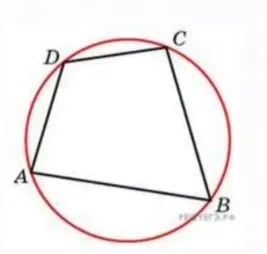
На рисунке одна окружность является периметром четырехугольника, поэтому выполняется условие, что сумма углов a и c равна сумме углов b и d, что равно 180 градусам.
Рассмотрим треугольник $ ABC $. Из вывода 1 мы знаем, что центр в клетке находится на пересечении биссектрис. Пересечение балок $ ak $ bm и $ bm в точке $ o $. Проведите перпендикуляр $ oh $ из $ o $ o $ к стороне $ bc $. Рисунок рисунка:.
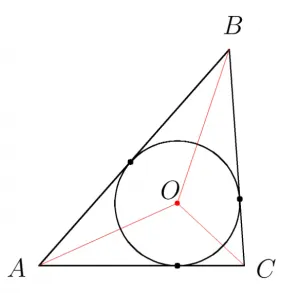
Вписанная окружность
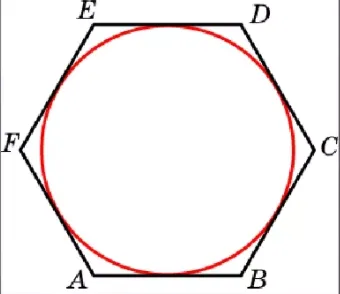
На этом уроке вы узнаете, что круг называется многоугольником, если все стороны многоугольника касаются круга, и что многоугольники описываются вокруг многоугольников. Докажите, что каждый треугольник может быть зарегистрирован как окружность. Однако не все четырехугольники могут быть зарегистрированы как круги. Вы также узнаете, что для каждой четверки суммы противоположностей равны.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к другим видеокурсам из этого набора, вам необходимо приобрести список и добавить его в свой личный кабинет.
Конспект урока «Вписанная окружность»
Сегодня, в этом уроке, вы узнаете, что такое зарегистрированный круг. Вы докажете, что можете регистрировать циклы для любого треугольника. Также будет показано, что не все четырехугольники могут быть зарегистрированы в окружности.
Мы только что рассмотрели касательные между прямой и окружностью. Напомним, что если существует окружность с центром в точке O и радиусом r, а точка A является общей точкой прямой и окружности, то существует только одна такая точка. Линия p, проходящая через точку касания, называется касательной линией. Радиус OA перпендикулярен точке контакта p.
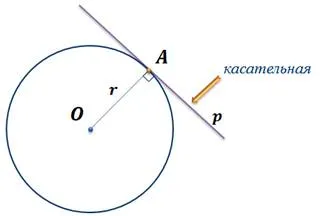
Вспомните теорему о том, что касательные, проведенные через окружность, равны и образуют угол, равный прямой, проходящей через точку и центр окружности.
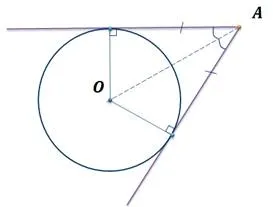
Таким образом, существует точка O, центр окружности, которая лежит на биссектрисе некоторого угла. Следовательно, окружность вписана в угол.
Как вы уже знаете, многоугольник имеет много углов и много граней.
Значение. Если все ребра многоугольника касательны к окружности, то окружность называется вписанной в многоугольник, а многоугольник — периметром многоугольника.
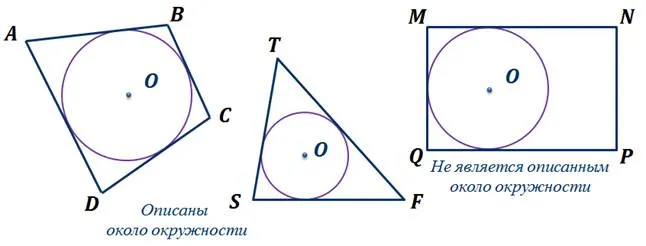
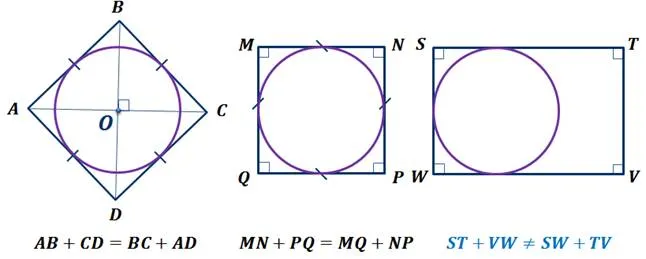
На этой схеме показаны четырехугольник ABCD, треугольник STF и четырехугольник MNPQ. Обратите внимание, что четырехугольник ABCD и треугольник STF нарисованы вокруг окружности с центром O. Этого нельзя сказать о четырехугольнике MNPQ. Он не является круговым, потому что сторона NP не является касательной к окружности.
Докажите теорему для окружности, вписанной в треугольник.
Теорема. В любом треугольнике можно нарисовать окружность, если.
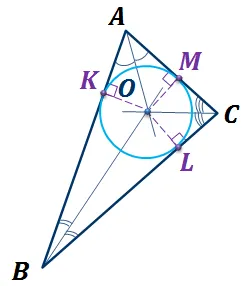
Окружность касается всех трех сторон
Окружность вписана в треугольник
1. в треугольник может быть вписана только одна окружность.
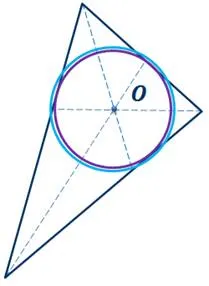
Предположим, что в треугольнике можно нарисовать две окружности.
Тогда центр второй окружности будет равноудален от всех сторон треугольника и будет являться точкой пересечения его биссектрис.
Однако все биссектрисы пересекаются в одной точке, то есть в точке, а радиус — это расстояние от точки до стороны треугольника, поэтому окружность, вписанная в треугольник, единичная.
2. в отличие от треугольника, не все четырехугольники могут быть вписаны в окружность.
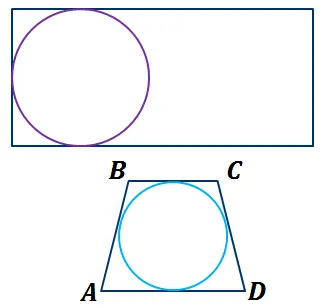
Рассмотрим прямоугольники, смежные стороны которых не равны.
В таком прямоугольнике можно «разместить» окружность, касательную к трем сторонам, но нельзя «разместить» окружность, касательную ко всем четырем сторонам. Другими словами, вы не можете нарисовать круг.
Это должно быть доказано.
Если окружность может быть записана на четырехугольнике, то ребра обладают следующими замечательными свойствами
В каждом очерченном четырехугольнике сумма противоположных сторон равна








