Доказательства. Противоположные углы α и β вписаны. Они лежат на дугах, которые дополняют друг друга в круге. Круг содержит 360°. Окружной угол равен половине дуги, на которой он лежит, поэтому сумма углов α и β равна 180°.
Вписанная окружность
Круг — это окружность, вписанная в геометрическую форму и касательная ко всем ее сторонам.
Круг можно записать в виде точной геометрической фигуры — четырехугольника.
В четырехугольниках окружность можно начертить только в том случае, если сумма длин противоположных сторон равна.
Во всех вышеперечисленных схемах круг может быть зарегистрирован только один раз.
Невозможно написать круги на прямоугольниках и прямоугольники на кругах. Это происходит потому, что круг не соприкасается со всеми краями этих фигур.
Геометрическая фигура, в которую вписана окружность, называется кругом.
Акроцикл — это треугольник, он является периметром, и три его стороны соприкасаются с окружностью.
Эндоцикл — это четырехугольник, проведенный вокруг окружности, четыре стороны которого соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих сторон равны, то окружность, может быть, вписана ( Теорема Пито ).
- Центр вписанной окружности и середины двух диагоналей лежат на одной прямой ( Теорема Ньютона, прямая Ньютона ).
- Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается окружность и любая из сторон четырехугольника.
- Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной в четырехугольник вычисляется по одной и той же формуле. Верное утверждение .
- Любой параллелограмм можно вписать в окружность. Неверное утверждение .
- В любой четырехугольник можно вписать окружность. Неверное утверждение .
- В любой ромб можно вписать окружность. Верное утверждение .
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение .
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение .
- Угол вписанный в окружность равен соответствующему центральному углу опирающемуся на ту же дугу. Неверное утверждение.
- Радиус вписанной окружности в прямоугольный треугольник равен половине разности суммы катетов и гипотенузы. Верное утверждение .
- Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение .
- Вписанная окружность в треугольник имеет в общем три общие точки со всеми сторонами треугольника. Верное утверждение .
Контур, вписанный в угол, — это окружность, проведенная внутри этого угла и соприкасающаяся с его сторонами.
Центр окружности, вписанной в угол, является биссектрисой этого угла.
К центру окружности, вписанной в угол, проведены два перпендикуляра.
Центральный угол окружности — это угол, вершина которого находится в центре окружности.
Диаметр, радиус, строка и длина дуги окружности измеряются в км, м, см, мм и других единицах.
Если окружность радиуса r вписана в многоугольник площадью S и ее полуокружность равна p, то справедлива причина: площадь вписанного круга равна произведению полуокружности и радиуса эндоцикла.
Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
Определение 1. Биссектриса угла — это радиус, который делит угол на две равные части.
Теорема 1 (Основные свойства биссектрисы угла). Каждая точка биссектрисы угла находится на одинаковом расстоянии от стороны угла (рис. 1).
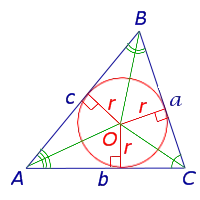
Доказательство Рассмотрим любую точку D на биссектрисе угла BAC и проведем перпендикулярные прямые DE и DF из D к ребру угла (рис. 1). Прямоугольные треугольники ADF и ADE равны, так как острые углы DAF и DAE равны, а косая сторона AD общая. Следовательно.
Доказательство.
Теорема 2 (обратная теорема теоремы 1). Если точки находятся на одинаковом расстоянии от сторон угла, то он лежит на биссектрисе угла (рис. 2).
Доказательство Рассмотрим любую точку D, которая лежит внутри угла BAC и находится на одинаковом расстоянии от края угла. Пусть DE и DF — перпендикуляры, проведенные из D к ребру угла (рис. 2). Прямоугольные треугольники ADF и ADE равны, так как перпендикулярные линии DF и DE равны, а косая сторона AD общая. Следовательно.
Доказательство.
Определение 2. Окружность называется вписанной в угол, если она является касательной к сторонам угла.
Теорема 3. Если окружность вписана в диагональ, то расстояние от вершины угла до точки касания окружности со стороной угла равно.
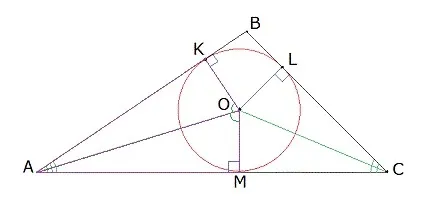
Доказательство Пусть D — центр окружности, вписанной в угол BAC, а E и F — точки касания окружности с боковыми линиями (рис. 3).
Прямоугольные треугольники ADF и ADE равны, так как кривые DF и DE равны (потому что радиус окружности — это радиус круга), а косая сторона AD — общая. Поэтому.
Доказательство.
Заявление. Теорему 3 можно сформулировать и по-другому. Отрезки касательной, проведенной по окружности из точки, равны.
Определение 3. Биссектриса треугольника — это часть биссектрисы угла треугольника, соединяющая вершины треугольника с противоположными точками.
Теорема 4. В каждом треугольнике все три биссектрисы пересекаются в одной точке.
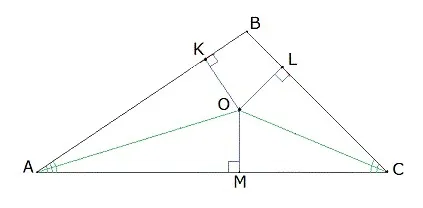
Доказательство Рассмотрите две биссектрисы A и C ABC и покажите их пересечение в точке O (рис. 4).
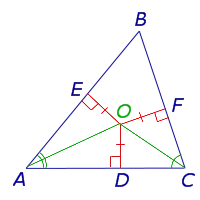
Из точки O оставьте перпендикуляры OD, OE и OF на сторонах треугольника. Так как O лежит на биссектрисе угла BAC, уравнение следует из Теоремы 1.
Согласно Теореме 1, если точка C лежит на биссектрисе угла ACB, то из уравнения следует.
Следовательно, уравнение верно.
Формулы для радиуса окружности, вписанной в треугольник
Уравнение для нахождения радиуса окружности, вписанной в треугольник, удобно приводить в виде следующей таблицы.
a, b, c — стороны треугольника, S — площадь, r — радиус конечной окружности, p — полусфера.
α — сторона равностороннего треугольника, r — радиус внутренней окружности.
где α, β и γ — стороны треугольника, S — площадь, r — радиус эндоцикла и p — полусфера.
Где α, β и γ — стороны треугольника, r — радиус эндоцикла, а p — полусфера.
Где α — сторона равностороннего треугольника, r — радиус эндоцикла.
| Произвольный треугольник |
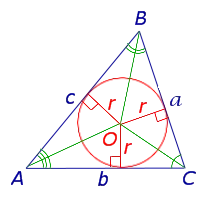 |
где α, β и γ — стороны треугольника, S — площадь, r — радиус эндоцикла и p — полусфера.
Где α, β и γ — стороны треугольника, r — радиус эндоцикла, а p — полусфера.
Где α — сторона равностороннего треугольника, r — радиус эндоцикла.
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5. Для любого треугольника
где a, b и c — стороны треугольника, а r — радиус эндоцикла, т.е. гемицикла (рис. 6).

Теорема 6. Для равнобедренных треугольников применимо следующее уравнение
где α — сторона равнобедренного треугольника, β — основание, а r — радиус эндоцикла (рис. 7).
Далее, для равнобедренных треугольников имеем
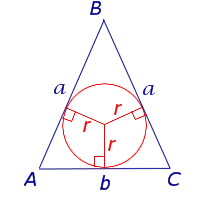
Теорема 7. Для равнобедренных треугольников применимо следующее уравнение
где α — сторона равнобедренного треугольника, а r — радиус эндоцикла (рис. 8).
Далее, в случае равносторонних треугольников, уравнение имеет следующий вид
описано в следующем разделе. В качестве упражнения читателю предлагается непосредственно вывести формулу радиуса окружности, вписанной в равносторонний треугольник. То есть не используйте общую формулу для радиуса окружности, вписанной в любой треугольник или равнобедренный треугольник.
Теорема 8. Для правильных треугольников уравнение
Доказательство Рассмотрим рисунок 9.
Четырехугольник CDOF является правильным треугольником с равными сторонами DO и OF, поэтому этот четырехугольник является четырехугольным квадратом. Поэтому.
Исходя из теоремы 3, экв.
Таким образом, также принимая во внимание теорему Пифагора, мы имеем
Заявление. В качестве упражнения читателю предлагается вывести, используя общую формулу для радиуса окружности, вписанной в любой треугольник, формулу для радиуса окружности, вписанной в прямоугольный треугольник.
Заявление. В качестве упражнения читателю предлагается вывести, используя общую формулу для радиуса окружности, вписанной в любой треугольник, формулу для радиуса окружности, вписанной в прямоугольный треугольник.
Формулы вычисления радиуса вписанной окружности
Параметры окружности, вписанной в геометрическую фигуру с тремя углами, можно вычислить по стандартным формулам. Радиус окружности определяется в зависимости от типа треугольника.
Произвольный треугольник
Радиус окружности, вписанной в треугольник, можно определить как площадь треугольника, деленную на его периметр.
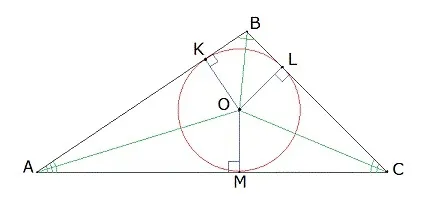
В данном случае α, β и γ — стороны геометрической фигуры с тремя углами, а S — ее площадь.
Прямоугольный треугольник
Радиус окружности, вписанной в прямоугольный треугольник, равен дроби, числитель которой равен сумме перпендикуляров минус количество виртуальных знаменателей2.
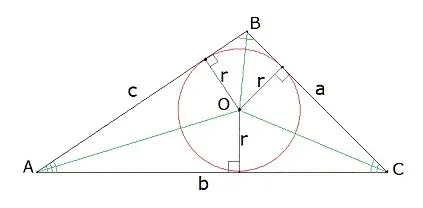
Уравнения a и b — катеты, а c — гипотенуза треугольника.
Равнобедренный треугольник
Радиус окружности, вписанной в равнобедренный треугольник, определяется по формуле
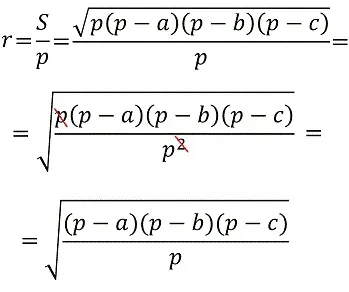
В данном случае a — это сторона, а b — основание треугольника.
Равносторонний треугольник
Расчет радиуса окружности, вписанной в равносторонний или правильный треугольник, производится по следующей формуле
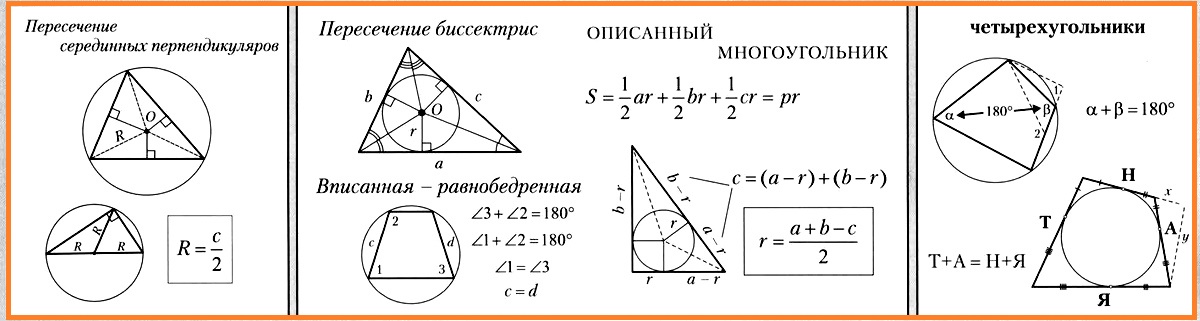
где α — сторона геометрической фигуры с тремя углами.
Как найти через высоту или стороны, примеры решения
Имеется геометрическая фигура с тремя углами, стороны которой равны 5, 7 и 10 см. Вам нужно определить радиус окружности, вписанной в этот треугольник.
Первое, что вам нужно сделать, это определить площадь треугольника. Для этого можно воспользоваться формулой Герона.

Затем примените формулу для расчета радиуса окружности.

ОТВЕТ: радиус окружности равен приблизительно 1,48 см.
Вам нужно вычислить радиус окружности, вписанной в равнобедренный треугольник. Стороны геометрической фигуры равны 16 см, а основание — 7 см.
Вам необходимо вычислить радиус, подставив известные значения в соответствующую формулу.
Доказательства.. Соедините центр внутренней окружности с вершиной треугольника, стороны которого равны α, β и γ. Получите три треугольника, радиусы которых являются высотами радиусов конечных циклов, выполненных в точках контакта. Площадь треугольника равна сумме площадей этих треугольников:.
Как вписывать окружность в треугольник
9 класс Оптическая геометрия. Ссылка 2 Круглые и внутренние круглые круги

Можно сформировать круг вокруг любого треугольника. Она проходит через все вершины треугольника. Вы уже знаете, что точки пересечения середин равноудалены от вершин треугольника. Он является центром региона.
Окружность может быть вписана в любой треугольник. Он касается всех сторон треугольника. Вы также знаете, что пересечение биссектрис треугольника равноудалено от сторон треугольника. Центр круга.
Но можно ли нарисовать круг вокруг произвольного прямоугольника? Если вы попытаетесь это сделать, то обнаружите, что нарисовать круг вокруг прямоугольника можно только в том случае, если прямоугольник Вы узнаете о свойствах вписанных и описанных четырехугольников и свойствах, позволяющих определить, можно ли описать область вокруг определенного четырехугольника и можно ли вписать в него окружность.
Кроме того, вы узнаете ключевую формулу для площади треугольника S =pr.
ТАБЛИЦА «Описанные и вписанные окружности»
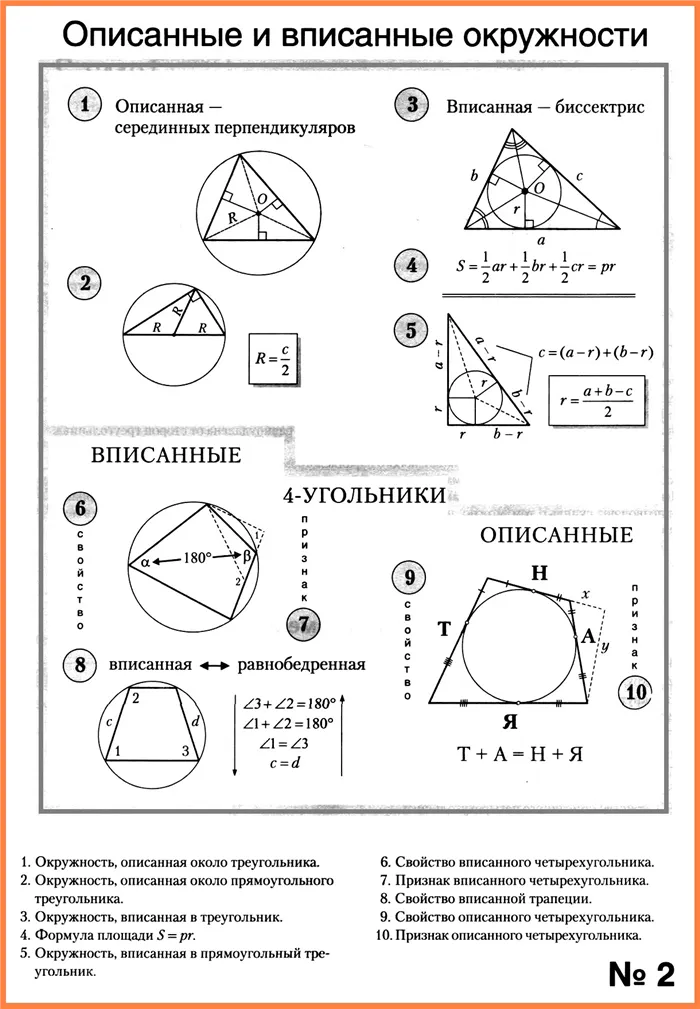
1. Окружность, описанная около треугольника.
Если окружность проходит через все вершины, она называется очерченной вокруг треугольника.
Теорема. Круг можно нарисовать вокруг любого треугольника, но только одного. Его центр лежит на пересечении перпендикулярных линий сторон треугольника.
Доказательства.. Точка пересечения средних перпендикуляров сторон треугольника равноудалена от его вершины (доказано в седьмой степени). Поэтому точка является центром окружности, а расстояние от нее до любой вершины равно ее радиусу.
Если существует еще один круг, то его центр равноудален от трех вершин, поэтому он совпадает с пересечением перпендикулярных линий, а его радиус совпадает с радиусом первого круга. Круги совпадают.
2. Окружность, описанная около прямоугольного треугольника.
Теорема. Периферийный центр окружности, проведенной вокруг прямоугольного треугольника, находится в середине гипотенузы, а радиус окружности равен половине гипотенузы.
Доказательства.. Мы знаем, что медиана прямоугольного треугольника, образованного из вершин прямого угла, равна половине гипотенузы (это было доказано в 7 классе). Поэтому середина гипотенузы является центром окружности, а ее радиус равен половине гипотенузы. То есть, R = c/2.
3. Окружность, вписанная в треугольник.
Считается, что окружность вписана в треугольник, если она является касательной ко всем сторонам треугольника.
Теорема. В любом треугольнике можно нарисовать окружность, имеющую только один Его центр лежит на пересечении биссектрис треугольника.
Доказательства.. Пересечение биссектрис треугольника равноудалено от сторон треугольника (доказано в классе 7). Если из этой точки провести перпендикуляр к стороне и очертить окружность радиусом, равным перпендикуляру, то сторона треугольника касается окружности в точке касания.
Если существует еще один эндоцикл, то его центр равноудален от всех трех сторон, поэтому он совпадает с пересечением биссектрис, а его радиус совпадает с радиусом первой окружности. Круги совпадают.
4. Формула площади S = рr.
Теорема. Площадь треугольника S = p r, где p — полуокружность треугольника, а r — радиус вписанной окружности.

Доказательства.. Соедините центр внутренней окружности с вершиной треугольника, стороны которого равны α, β и γ. Получите три треугольника, радиусы которых являются высотами радиусов конечных циклов, выполненных в точках контакта. Площадь треугольника равна сумме площадей этих треугольников:.
где p — полуокружность треугольника.
Это уравнение применимо ко всем многоугольникам, которые могут быть вписаны в окружность, то есть ко всем окружностям. Доказательство аналогично.
5. Окружность, вписанная в прямоугольный треугольник.
Теорема. Радиус окружности, вписанной в правильный треугольник, находится по уравнению r = (a + b —c)/2.








