Острый экстремум Важно! Процесс нахождения точек острого экстремума функции называется дифференцированием и используется как в школьном курсе изучения алгебры и начала анализа, так и в ходе освоения высшей математики в университете.
Что такое экстремумы функции: критические точки максимума и минимума
Из этой статьи читатель узнает о крайних значениях функциональных цен и особенностях их реального использования. Изучение этих понятий необходимо для понимания основных принципов высшей математики. Эта тема является основой для более тщательного изучения уроков.
Существует множество определений понятия «крайности» на школьных уроках. Цель данной статьи — дать наиболее полное и ясное понимание этого термина для тех, кто не посвящен в тему. Таким образом, этот термин означает степень, в которой пространство функций имеет минимальное или максимальное значение на множестве.
Экстремумы — это одновременно минимальное и максимальное значения функции. Существует различие между некоторым и максимальным значениями, которые являются концами аргументов на графике. Ключевые научные значения:.
- экономика,
- статистика,
- биология,
- машинное управление,
- эконометрика.
Точки экстремума играют важную роль в определении последовательности той или иной функции. Система координат графика лучше всего иллюстрирует изменение экстремальных точек при изменении функции.
Это интересно! Свойства естественного логоса: график, основание, функция, ограничение, формула, область определения.
Экстремумы производной функции
Существуют также такие явления, как «деривативы». Необходимо определить экстремальные точки. Важно не путать минимальные или максимальные баллы с максимальными и минимальными значениями. Это разные понятия, но могут показаться похожими.
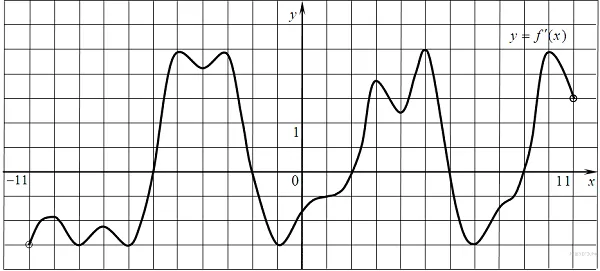
Производные функций
Значение функции является важным фактором при определении того, как найти точку максимума. Деривативы возникают не из стоимости, а только из крайних позиций в том или ином классе.
Сама производная определяется на основе конкретной точки экстремума, а не самого высокого или самого низкого значения. В российских школах различие между этими двумя понятиями недостаточно четкое и влияет на понимание предмета в целом.
Это интересно! Как доказать и подставить постоянный интеграл от нуля, постоянной и
Острый экстремум
Рассмотрим такие понятия, как «острое акне». Сегодня существует резкий минимум и кислотный максимум. Определение следует российской классификации критических точек функции. Концепция экстремальных точек является основой для нахождения важных точек графика.
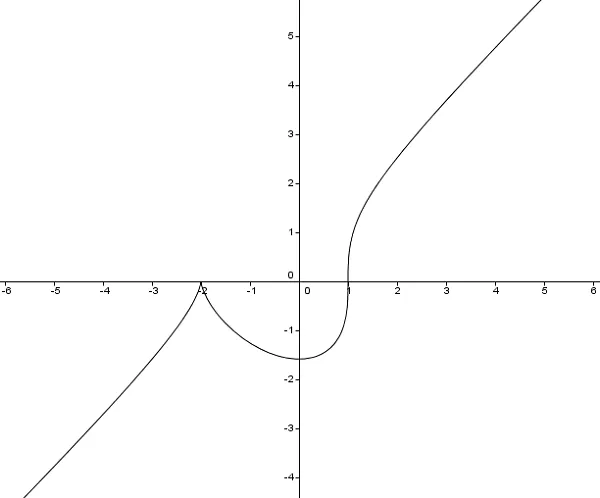
Нахождение знаков наиболее экстремальных функций называется дифференцированием и используется как на школьных уроках алгебры и принципов анализа, так и в высшей математике в колледже.
Рассмотрим непрерывные функции, которые не изменяются монотонно, т.е. функции, которые возрастают на одних интервалах и убывают на других. Графики этих функций можно представить, как показано на рисунке 9.
Монотонность функции. Точки экстремума и экстремумы функции
Рассмотрим функции. Предположим, что они непрерывны на всей числовой прямой.
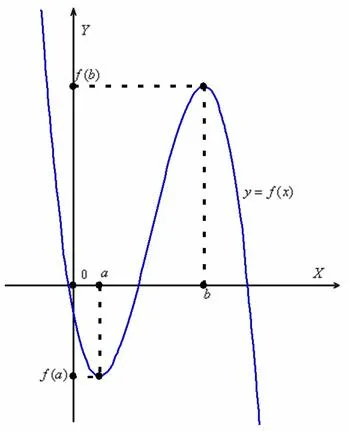
В любом случае, избегайте возможных иллюзий, особенно для читателей, которые недавно познакомились со спецификой функций. Нас не интересует положение графика функции по отношению к осям (выше, ниже или в точке пересечения осей). Чтобы сделать его наглядным, мысленно уберите оси и оставьте только один график. Это то, что нас интересует.
В случае двух интервалов, связанных отношениями, функция возрастает с течением времени, если применяется неравенство. Это означает, что большим значениям аргумента соответствуют большие значения функции, а график функции идет «снизу вверх». Демонстрационные функции растут в пространстве.
Аналогично, в случае двух пространств функция убывает сразу, так что неравенство применимо. Другими словами, меньшее значение аргумента означает меньшее значение функции и ее графика «сверху вниз». Наша актуальность уменьшается с интервалом.
Если функция возрастает или убывает в течение некоторого периода времени, она называется строго монотонной в течение этого периода. Что такое монотонность? Понять монотонность — буквально.
Вы также можете определить не убывающую функцию (свободное условие в первом определении) и не возрастающую функцию (свободное условие во втором определении). Не определяющие или не возрастающие в этой точке функции называются монотонными (строгая монотонность является частным случаем «простой» монотонности).
Теория также рассматривает другие подходы к определению возрастающих/убывающих функций, включая полупересечения и пространства, но соглашается работать с открытыми пространствами с определениями категорий, чтобы не лить масло и масло на голову. Многие. Достаточно для решения многих практических задач.
Поэтому в моих статьях формулировка «монотонность функций» почти всегда скрытаИнтервал. Строгая монотонность (строго возрастающая или строго убывающая функция).
Близость к точке. Одно слово, и ученики разбегаются, чтобы спрятаться и скрыться в углах от страха. … (После публикации ограничений Коши они, вероятно, уже не прячутся, а слегка дрожат =) Не волнуйтесь, в настоящее время нет никаких доказательств математического анализа — мне нужна была среда, чтобы сформулировать более строгое определение экстремальных точек. Отзыв:.
Окрестности точки — это пространство, заключенное в этой точке, и для удобства пространство часто считается симметричным. Например, точка и ее типичная окрестность: соответствующее определение: a
Точка строго называется точкой максимума, если существует точка, смежная с каждым значением, удовлетворяющим неравенству, кроме самой точки. В нашем конкретном примере это все.
Если при выполнении неравенства точка индуцируется на все значения, кроме самой точки, то точка называется строго минимальной. План — это пункт «А».
Как найти интервалы возрастания, убывания, точки экстремума и экстремумы функции?
На самом деле, многие правила уже известны и понятны из уроков по производным понятиям.
На мгновение задумайтесь о том, что функции различны. Итак: .
— Если производная находится на постоянном промежутке, то функция возрастает на этом промежутке, и
— Если производная находится в постоянном периоде, то функция убывает в этом периоде.
Примечание: обратное также применимо.
Предположим, что точкаПринадлежит к области определения функции. Эта точка называется критической, если производная равна нулю или не имеет ценности. Эта критическая точка может быть крайней. Это может быть так, а может и не быть. Необходимые и достаточные условия для существования экстремума будут рассмотрены в ближайшее время.
Но сначала.… Мы будем практиковать кошачьи … Давайте рассмотрим самый простой пример. В заключение мы рассмотрим теоретическую статью о дифференциации и продолжим изучение других жертв анализа. В то же время, есть возможность сделать небольшой самоконтроль — как вы запомнили график важных функций, на что он похож? Конечно, если это сложно, вам придется открыть первый урок в следующей вкладке и щелкать туда-сюда, комментируя.
Производная кубической функции неотрицательна: для каждого «x». Действительно, кубическая притча «снизу вверх». Конечно, скорость изменения функции равна нулю, что обозначается производной. Кстати, вот важный момент: нет примера максимального или минимального значения функции.
Тот факт, что функция существует в пространстве и выводится через ее неравенство, ясно показывает, что «корень из X» строго возрастает в критической точке. С геометрической точки зрения, общих касательных не существует. Однако в теории рассматривается одна производная So -Caled, и в этой точке существует производная с касательной по часовой стрелке. Желающие понять это более подробно могут прочитать первый том «Матана».
Примечание: Согласно информации, указанной в первом абзаце, эта точка не является точкой минимума функции (но является ею «по косвенным признакам»). Дело в том, что определение максимума и минимума предполагает существование функции как слева, так и справа от конкретной точки. Также крайние точки дуги и площади лука не считаются крайними точками (см. ниже).
Стандартное преувеличение — «сверху вниз». Это означает, что функция уменьшается во всем своем диапазоне. На это указывают его производные: для каждого «х», кроме нуля. Кстати, этот момент нельзя считать несущественным. Это происходит потому, что функция не может быть определена там.
Экспоненциальная функция имеет место на всей числовой прямой (строгие неравенства применимы для любого значения ‘x’). Глядя на производные, легко сделать вывод, что функция уменьшается.
Что вы имеете в виду под физическим логарифмом?Сегодня вечером.; увеличить: в пространстве.
Нарисуйте/напечатайте рядом или на картинке (или представьте в уме) график функции и ее производных. Если график синагоги лежит на оси, то синус увеличивается. Напротив, если график лежит ниже положения леса, синус уменьшается. В точке, где косинус пересекает ось (), синус достигает минимума или максимума.
Зачем исследовать функцию с помощью производной?
Чтобы лучше понять, как выглядит график этой функции: куда идет «снизу вверх» от «снизу вверх».. Не все функции так просты — в большинстве случаев неясно, является ли график определенной функцией или нет.
Затем пора переходить к более содержательным примерам, проверить алгоритм и найти монотонность и экстремумы функции.
Нахождение последовательного/ убывающего промежутка и экстремумов функции
(1) Первый шаг включает в себя поиск полей в определении функции и маркировку точек разрыва (если таковые имеются). Этот шаг в некоторой степени типичен, поскольку функции непрерывны на всей числовой прямой. Однако в некоторых случаях здесь есть много волнующего, поэтому давайте не будем игнорировать это и возьмем абзац.
2) Второй пункт алгоритма.
Функция в любой заданной позиции должна быть выделена, чтобы выявить новое значение. Важно понимать, что для точки, обращенной в ноль, не является основным принципом нахождение другой точки.
Первое достаточное условие экстремума
(Крайнее первое компетентное условие).
Для функции $ y = f(x)$ предположим, что выполняются следующие условия.
- функция непрерывна в окрестности точки $x_$;
- $f^<\prime>\ɑLeft (x_ \Right) = 0 $ или $ f ^^<\prime>\left(x_\right)$ не существует;
- производная $f^<\prime>(x)$ при переходе через точку $x_$ меняет свой знак.
Далее, в точке $ x = x_ $ функция $ y = f(x)$ имеет экстремальное значение. Это минимальное значение, при котором производная меняет знак с отрицательного на положительный при прохождении через точку $ x_ $. Производная меняет знак с положительного на отрицательный при прохождении через точку $ x_ $.
Для производной $f^.<\prime>(x)$ не меняет знак при прохождении через точку $ x_ $, экстремальное значение в точке $ x =x_$ отсутствует.
Поэтому для исследования терминальной функции $ y = f(x)$ необходимо
- найти производную $f^<\prime>(x)$;
- найти критические точки, то есть такие значения $x$, в которых $f^<\prime>(x) = 0$ или $f^.<\prime>(x)$ не существует;
- исследовать знак производной слева и справа от каждой критической точки;
- найти значение функции в экстремальных точках.
Задание. В крайних случаях исследуйте функцию $ y(x) = x ^-1$.
Разрешение. Найдите производную этой функции.
Далее найдите критическую точку функции, решив уравнение $ y ^.<\prime>(x) = 0 $:.
Первая производная определена во всех точках. Следовательно, существует критическая точка $ x =0$. Постройте эту точку на координатной прямой и определите знак производной по обе стороны от этой точки (для этого возьмите любое значение из каждого интервала и найдите значение производной в выбранной точке. (Знак ценности, которую мы получаем):.
Производная поменяла знак с «-» на «+» при прохождении через точку $ x = 0 $, поэтому функция достигает минимума (или минимального значения) в этой точке и $ y_.<\min >= y(0) = 0 ^ -1 = -1$.
ПРИМЕЧАНИЯ. Вы также можете задать монотонный интервал для функции. Производные интервала $(-\ infty; 0)$ $ $ y ^<\prime>(x)™ lt 0 $, функция $ y (x) = x ^ -1 $ убывает на этом интервале — интервале $ (0; + \ infty)$ производная $ y ^<\prime>(x) > 0 $, поэтому функция возрастает до него.
Ответ. $ y_<\min >= y(0) = -1 $
Второе достаточное условие экстремума
(Крайнее второе возможное условие).
Для функции $ y = f(x)$ предположим, что выполняются следующие условия.
- она непрерывна в окрестности точки $x_$;
- первая производная $f^<\prime>(x)=0$ в точке $x_$;
- $f^<\prime \prime>(x) \neq 0$ в точке $x_$ .
Затем, в точке $ x_ $ достигается экстремальное значение и $ f ^<\prime \prime>\ {left (x_ \ right) > 0 $, тогда при $ x =x_$ функция $y= f (x)$ имеет минимум, если $ f ^<\prime \prime>\ слева (x_ \ справа)™ lt 0 $, то в точке $ x =x_$ функция $y= f(x)$ достигает своего максимума.

Мы уже помогли 4 372 школьникам и студентам сдать на отлично письменные работы от решения задач до дипломных работ! Узнайте, сколько стоит ваша газета за 15 минут!
Задание. Исследуйте функцию экстремального значения $y(x) = \ frac-1>+1>$ через вторую производную.
Разрешение. Найдите первую производную заданной функции:.
Найдите точку, в которой первая производная равна нулю.
Вторая производная этой функции:.
В неподвижной точке $x= 0 $ найдите вторую производную $ y ^<\prime \prime>(0) = -\ frac> = 4> 0 $ Следовательно, в этой точке функция достигает минимума и $ y_<\min >= y (0) = \ frac-1> +1>=-1$.
Ответ. $ y_<\min >= y(0) = -1 $
Остались вопросы?
Экстремальные значения — это значения функции на определенном интервале, когда функция достигает минимального или максимального значения. Понятие экстремального значения или минимума/максимума относится к значению функции (y).
Точка экстремального значения, т.е. когда максимальное/минимальное значение функции достигается в определенном интервале, называется точкой экстремального значения. Видно, что когда экстремальное значение достигает минимума, его называют точкой минимума, и наоборот, когда оно достигает максимума, его называют точкой максимума. При определении точки экстремального значения (или минимума/максимума) подразумевается x, которое достигает минимального или максимального значения.
Если существует точка V, которая является окрестностью (x₀—V; x₀+ V) вышеуказанной точки, то любая точка x₀ определяется как точка минимума функции y = f(x). x.<> x₀ выполняется следующее неравенство.
Термин «минимальное значение функции» относится к точке функции с наименьшим значением среди всех значений, принятых в любой из соседних точек. Другими словами, это означает, что если функция перестает убывать в некоторой точке и, наоборот, возрастает, то это точка минимума функции.
Как можно вычислить значение функции y=x⁴-4x³+6x²-4x, которая достигает точки минимума?
Ответ на этот вопрос заключается в нахождении точки минимума функции, в которой ее значение перестает падать. Это можно сделать следующим образом.
Предполагая, что минимальное значение этой функции равно нулю, мы можем переписать уравнение в следующем виде
Давайте уменьшим это уравнение на четыре.
Полученное уравнение также можно записать в следующем виде после замены членов
Перепишите сумму и удалите третий порядок.
Это же уравнение можно записать в следующем виде
Сложим суммы x и -3x:.
Теперь это уравнение можно переписать и упростить следующим образом.
Символы ‘+’ и ‘-‘ обозначают значения производных.
Проведя вычисления, мы обнаруживаем, что x=1, что является точкой минимума функции.
у=1⁴-4*1³+6*1²-4*1= 1-4 +6-4 = -1
Точка максимума — это значение x, при котором производная меняет знак с положительного на отрицательный. Зная это, мы можем перейти к нахождению точки максимума функции, заданной в задаче.
Чтобы сделать это, начните с нахождения производной с помощью следующего уравнения
Замените и возьмите значение, данное в произведении: y’=(-(x²))
y’=(-(x²+ 484)-2x)/(x²+ 484)²=(-x²-484-2x)/(x²+ 484)²
Теперь нам нужно приравнять производные к 0 и начать решать полученное уравнение.
Упрощая уравнение, мы имеем
Давайте уберем отрицательную часть уравнения:.
У нас есть функция y=x²-3x+2, которую также можно переписать в следующем виде
miny = —0,25 (если x-1,5 = 0)
Можно сделать вывод, что x = 1,5.
Запишите производную этой функции.
Тогда приравняйте его к 0.
Это позволяет нам заключить, что
Для x = 3/2 мы знаем, что для производных y’> 0 функция имеет возрастающий порядок.
x = 3/2 = 1,5 — единственная крайняя точка, которая является точкой минимума.








