Эта статья в первую очередь предназначена для студентов и магистрантов, имеющих небольшой опыт программирования или не имеющих его вовсе, но не обладающих достаточными знаниями геометрии, чтобы написать игру.
Векторы на ЕГЭ по математике. Действия над векторами
Обычное определение: «Вектор — это отрезок направления». Обычно знания выпускников о векторах этим и ограничиваются. Кому нужны «направленные секции»?
И действительно, что такое вектор и почему? Прогноз погоды. ‘Ветер северо-западный, 18 метров в секунду’. Согласен, важны как направление ветра (куда он дует), так и его мера скорости (т.е. абсолютное значение).
Значения без направления называются ступенчатыми значениями. Масса, работа и заряд никуда не направлены. Они могут характеризоваться только числовым значением, например, «сколько килограммов» или «сколько джоулей».
Физические величины, которые имеют направление, а также абсолютное значение, называются векторными величинами.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения
Напомним, что физические размеры представлены латинскими или греческими буквами. Стрелка над буквой указывает на то, что величина является вектором.
Вот другой пример. Автомобиль движется из A в B. Конечный результат — его перемещение из точки A в точку B, то есть перемещение на вектор
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, что конец вектора находится там, где стрелка. Длина вектора — это длина его сегмента. Он символизируется следующим образом:.
До сих пор мы имели дело со ступенчатыми величинами в соответствии с правилами арифметической алгебры и элементарной алгебры. Игрок — это новая концепция. Это еще одна категория математических объектов. У них есть свои правила.
Мы ничего не знали о цифрах. Мы начали встречаться с ними в старших классах. Числа демонстрируют умение сравнивать, складывать, вычитать, умножать и делить. Мы узнали, что существует число один и число ноль. Далее мы ввели векторы.
В векторах нет понятий «больше» и «меньше», так как векторы могут иметь различные направления. Сравнивать можно только длины векторов.
Однако у векторов есть понятие равенства. Векторы с одинаковой длиной и одинаковым направлением называются равными. Это означает, что вектор может двигаться параллельно в любой точке плоскости. Единичный вектор — это вектор длины один. Нулевой вектор — это вектор длины ноль. Это означает, что начало и конец совпадают.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y, абсцисса и ордината. Вектор также задается двумя координатами:
Здесь координаты векторов описаны в скобках. Они просты: координаты конца вектора минус координаты его начала.
Учитывая координаты вектора, его длину можно найти по следующему уравнению.
Сложение векторов
Существует два способа сложения векторов.
1.1. правило прямоугольника. Чтобы добавить вектор, поместите обе начальные точки в одну точку. Достройте прямоугольник до прямоугольника и проведите прямоугольную диагональ из той же точки. Это будет сумма векторов.
Помните миф о лебеде, раке и щуке? Они старались изо всех сил, но не смогли сдвинуть тележку с места. Это происходит потому, что векторная сумма сил, приложенных к тележке, равна нулю.
2.2. второй способ сложения векторов — это правило треугольника. Вы получите те же самые векторы. Добавьте начало второго вектора к концу первого вектора. Затем соедините начало первого вектора с концом второго вектора. Это сумма векторов.
Это же правило можно использовать для сложения многих векторов. Добавляйте их по одному, а затем соедините начало первого вектора с концом последнего вектора.
Представьте, что вы переходите из пункта А в пункт Б, из пункта Б в пункт В, из пункта В в пункт Г, а затем в пункты Е и F. Конечным результатом этих действий является переход от A к F.
Сложение векторов будет выглядеть следующим образом
Умножение вектора на число
При умножении вектора. Если k меньше нуля, то он направлен в ту же сторону, что и вектор.
Векторы можно умножать друг на друга, а также на число.
Степенное векторное произведение — это произведение вектора векторов на его косинус.
Примечание — при умножении двух векторов вместе получается один шаг, т.е. число. Например, в физике механическая работа равна масштабируемому произведению двух векторов — мощности и перемещения.
Если векторы вертикальны, то масштабируемое произведение равно нулю. Поэтому масштабируемость выражается в терминах векторных координат.
Из вида масштабируемого произведения можно найти угол между векторами.
Этот тип особенно полезен для стереометрических измерений. Например, в вопросе 14 экзамена по математике требуется найти угол между прямой линией или линией, пересекающей прямую линию, и одним уровнем. Векторные методы часто решают задачи так же быстро, как и 14.
В школьной математике изучаются только масштабируемые векторы. В дополнение к масштабируемым произведениям, векторные произведения также существуют, когда два вектора перемножаются, образуя вектор. Любой, кто изучал физику, покажет, что такое силы Лоренца и Ампера. Типы сил, которые вы найдете, включают векторы-векторы.
Векторы — очень полезные математические инструменты. Это будет показано в первом уроке.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: книга Анны Марковой + 70-часовой видеокурс. -144 часа семинаров: 8 онлайн-семинаров в месяц с Анной Марковой. — Рабочий тренажер (800+ заданий): автоматическое + ручное управление. -Контакт с Анной Малковой (разговор и электронная почта). Использование -9 репетиций: ежемесячно. — Контроль: страница успеваемости ученика, справка для родителей. — Личный счет.
Это определение пытается косвенно предоставить руководство по геометрии при введении понятия равенства векторов. Однако здесь есть противоречие — в руководстве сначала дается определение фиксированных векторов, а затем объясняется, как использовать свободные векторы.
Длина вектора
иВекторы. a b→ — числа, большие или равные 0 и равные длине отрезка AB.
Длина вектора a b→ обычно обозначается как a b→.
Понятия коэффициент вектора и длина вектора эквивалентны, так как их символика соответствует символу сигнала. Поэтому длину вектора также называют его коэффициентом. Однако более уместно использовать термин «длина вектора». Очевидно, что длина нулевого вектора получает значение ноль.
Коллинеарность векторов
Два вектора, лежащие на одной прямой или параллели, называютсяКоллинеарный. .
Два вектора, не лежащие на одной прямой или параллели, называютсяБез стека. .
Следует помнить, что нулевые векторы могут принимать любое направление и поэтому всегда прилипают к другим векторам.
Концентрические векторы также можно разделить на две категории: совместный контроль и направление.
Направление векторов
Векторы совместного развития Они показаны как два сложенных вектора A→ и B→B→ эти векторы показаны как →↑↑→B→B→.
Векторы в противоположных направлениях Имеются два сложенных вектора A→B→, направления которых не совпадают. То есть, они противоположны. Эти векторы показаны как →↓↓B→.
Считается, что нулевые векторы сосуществуют со всеми другими векторами.

При строгом порядке записи каждый набор чисел создает только один вектор, а каждый вектор связан только с одним числом. Это означает, что если есть векторные координаты, то их нельзя смешивать.
Вектор. Определение и основные понятия
Вектор — это отрезок направления, т.е. отрезок с длиной и определенным направлением. Векторы графически представляются в виде прямых отрезков определенной длины.
Вектор с началом в точке ⌘ (a \) и концом в точке ⌘ (b \) называется вектором ⌘ (⌘ vec \). Векторы также обозначаются строчными буквами. \ (⌘ ⌘ vec \).
Направление вектора (от начала к концу) отмечается на чертеже стрелкой.

Нулевой вектор
Нулевые векторы обычно обозначаются как ⌘ (⌘ vec \).
Нулевые векторы имеют длину, равную нулю.
Каждую точку в пространстве можно также рассматривать как вектор. Этот вектор называется нулевым вектором. Начало и конец нулевого вектора совпадают и не имеют определенного направления.
Нулевой вектор — это вектор совпадения принципа и конца.
Равные вектора
Это означает, что два вектора равны, если они имеют общее направление и равную длину.

Если вам понравился материал и вы считаете его полезным, поделитесь им со своими друзьями!
Сумма двух векторов a и b является третьим вектором c, проведенным из начала a в конец b, если начало вектора b совпадает с концом вектора a. Разность двух векторов a и b является вектором c, если c = a — b.
Произведением вектора u ≠ 0 с числовым значением λ ≠ 0 является вектор w, мерой которого является|
Пошаговое произведение векторов u и v является произведением КОСИНЕЙ данной единицы.
Вектором векторов u и v называется третий вектор w, который равен произведению векторов u и v на полутон угла i и перпендикулярен им.
Смешанное произведение трех векторов u, v и w — это масштабируемое произведение вектора u с векторами v и w.

Тригонометрическое тождество — это уравнение, которое определяет связь между синусом, косинусом, тангенсом и угловой курицей, и одна из этих функций может быть найдена, если известны другие функции.
Равный объем газа (V) при одинаковых условиях (температура T и давление P) содержит одинаковое количество молекул.
О сайте
На нашем сайте представлено множество полезных калькуляторов, инверторов, таблиц и справочных материалов для базового сектора.
Самый простой способ подсчета — использовать соответствующие онлайн-инструменты. Используйте поиск, чтобы найти нужный инструмент на нашем сайте.
calcsbox.com.
На этом сайте используется технология латекса. Поэтому дождитесь полной загрузки страницы и правильного отображения типа и формулы.
Однако это не так. Фактически, значения координат вектора численно равны этой разности. Однако определение векторных координат принципиально отличается от определения координат точки.
Как записывать
Векторы могут быть записаны в столбцах или строках. Чтобы записать вектор в строке, обозначьте его буквой, поставьте черту, раскройте скобку и напишите координаты вектора через запятую. Для записи в столбцах координаты вектора должны быть заключены в скобки или скобки — оба варианта приемлемы.
При строгом порядке записи каждый набор чисел создает только один вектор, а каждый вектор связан только с одним числом. Это означает, что если есть векторные координаты, то их нельзя смешивать.
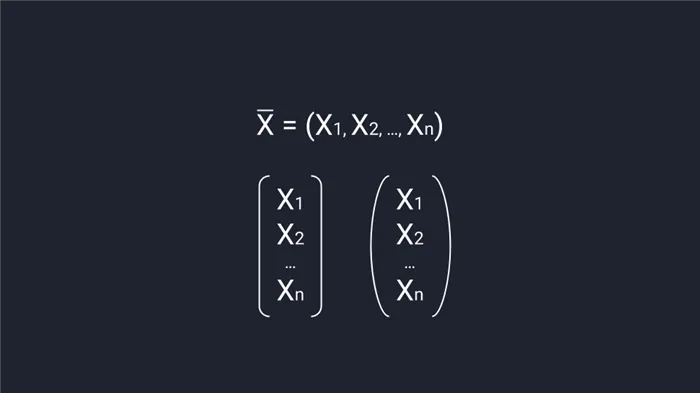
Как писать векторы
Скаляр
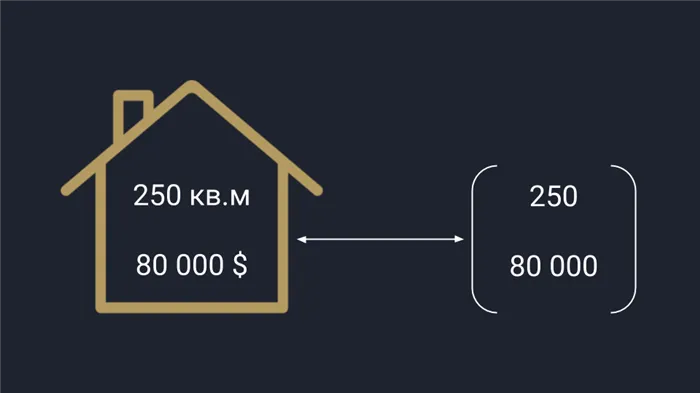
В дополнение к понятию векторов существует понятие масштабов. Шаг — это простое число. Можно сказать, что шаг — это вектор, состоящий из координат.
Помните физику? Существуют масштабные и векторные величины. Масштабные величины определенным образом представляют ситуацию, например, температуру. Векторные величины также представляют направление.
Как изображать
Вектор чисел (шкала) представлен в виде точки на числовой прямой.
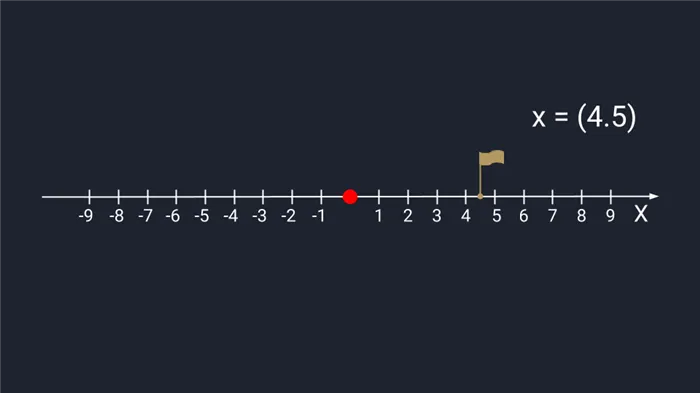
Графическое изображение шкалы. Он указан в скобках.
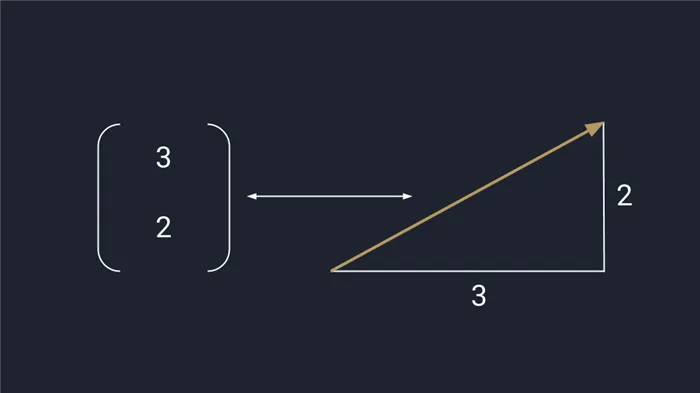
Векторы двух чисел представлены в виде точек на плоскости осей x и y. Числа определяют координаты векторов в пространстве. Это команда для перемещения от конца вектора к стрелке. Первое число указывает на расстояние, пройденное по оси X, второе — по оси Y; положительное число на оси X означает движение вправо, отрицательное — влево. Положительные числа на оси Y указывают на увеличение, отрицательные — на уменьшение.
-5 и 4 числа для представления вектора. Чтобы найти нужную точку, нужно пройти пять шагов влево по оси X, а затем четыре шага вверх по оси Y.
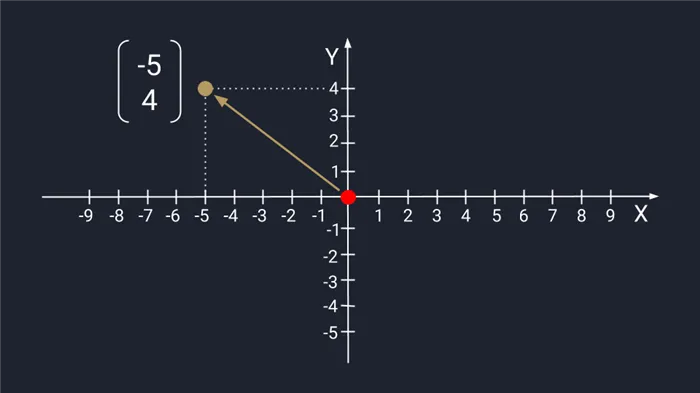
Графическое представление вектора двумерных чисел
Вектор из трех чисел представлен в виде точки в плоскости осей X, Y и Z; ось Z откладывается перпендикулярно осям X и Y. Перемещение по осям X и Y, третья — точка, которую нужно переместить по оси Z. Каждый триплет создает уникальный вектор в пространстве, и для каждого вектора может существовать только один триплет.
Если вектор состоит из четырех или более чисел, то теоретически он строится аналогичным образом. Получаются координаты и строится n-мерное пространство для нахождения нужной точки. Это трудно представить, и для обучения это не понадобится.
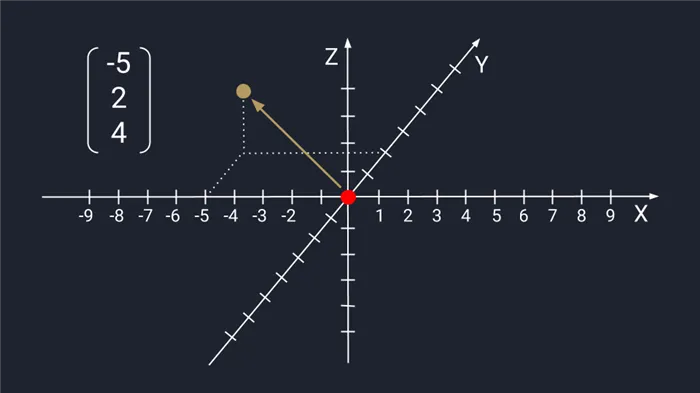
Графическое представление вектора трехмерных чисел. Например, координаты -5, 2 и 4.
Помните, что все эти записи и алгебраические представления не имеют ничего общего с реальным трехмерным пространством. Вектор — это абстрактное число простых чисел, построенных в строгом порядке. Векторы не интересуются тем, сколько существует чисел или как люди их представляют. Для ясности и удобства они просто представляют их.
Например, вектор может содержать 99 координат. Чтобы представить их, вам потребуется 99 измерений, что очень проблематично на бумаге. Для векторов, однако, это не проблема: вы можете умножать и складывать два координатных вектора так же, как и для координатного вектора 99999999. Принцип тот же самый.
И зачем нам это всё
Векторы — это «кирпичики», на которых строится наука о данных и машинное обучение. Например:.
- На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
- Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.
Векторы также используются в компьютерной графике, аудио, инженерном деле и почти во всех компьютерных программах.
Также напомним, что векторы — это не сложные абстракции, а просто наборы чисел, расположенных в определенном порядке. То, что мы называем вектором, является лишь нюансом этого термина.
Наука о данных использует математическое представление векторов. Программисты могут обрабатывать данные и отображать результаты. В отличие от своего физического представления, математические векторные стрелки привязаны к системам координат X и Y. Эти стрелы не блуждают в пространстве, а исходят из нулевой точки.
Что такое вектор
В школьных курсах геометрии векторы определяются так: «Вектор — это отрезок направления». Это определение почти всегда верно. И теперь я не согласен с системой школьного образования и даю другое определение вектора. Проведем два направленных отрезка одинаковой длины, направленных в одну сторону параллельными прямыми.

Примечание: Более подробную информацию о приведенном мною определении см. в конце статьи.
Равенство векторов
Если задуматься, то все направления, которые появляются в параллельных линиях одинаковой длины и в одном направлении, имеют одинаковое направление и одинаковую длину. Следовательно, все эти указанные отрезки представляют один и тот же вектор. Здесь показано определение equality2vector.
Это определение указывает, когда намеренные секции ARBITRARY продолжают представлять тот же вектор, который был представлен до переноса. Это свойство активно используется в действии вектора.
Длина вектора

Длина вектора — это длина направленной части, представляющей конкретный вектор. Длина вектора показана на следующем рисунке.
-
Если отрезки, представляющие 2 вектора, лежат на параллельных прямых, то векторы, представленные данными отрезками, называют коллинеарными.
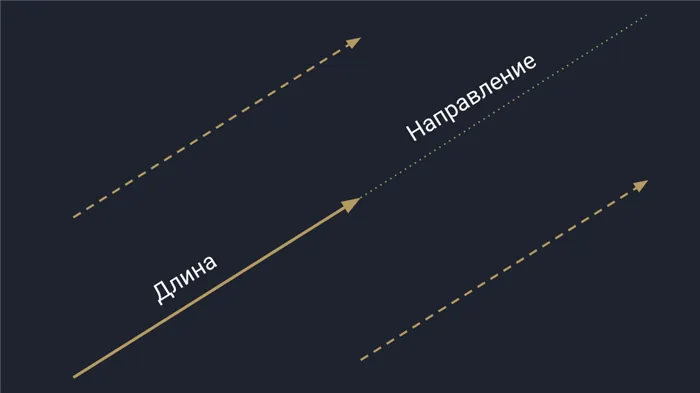
На диаграмме каждая пара векторов является прямолинейным вектором.
Написано:.








