Также удобнее выразить деление как обратное умножение и использовать распределительное свойство умножения по отношению к сложению, если числа достаточно большие.
Урок «Деление обыкновенных дробей на натуральное число»
Отметим, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, обучение и воспитание обучающихся с ограниченными возможностями здоровья организуется как в отдельных классах, так и в группах с другими обучающимися.
Тема урока: «Деление обычных фрагментов на натуральные числа».
Класс: 5Б
Цель курса: изучить правила разбиения фрагментов с натуральными числами и применять их при решении упражнений.
Сформулировать правила деления дробей на натуральные числа.
уметь применять их при решении примеров, и
Продолжайте работать над развитием вычислительных навыков.
Развитие познавательного интереса, математическая культивация.
Развитие делового мышления, элемент творчества через поисковую деятельность студентов, умение использовать современные технологии в обучении (интерактивные столы, ПК).
Тип курса: комбинированный.
Методы преподавания: частично изучены.
ПРОГРАММНЫЕ ТРЕБОВАНИЯ: это курс 77 по теме «Обычные дроби» (всего 80 часов). Учащиеся уже знают, как складывать и вычитать дроби с одинаковым знаменателем. Они знают основные свойства дробей, умеют умножать дроби на натуральные числа и сокращать дроби. В ходе изучения курса студенты должны установить правила деления дробей на натуральные числа.
Учащиеся знают, как делить дроби на натуральные числа.
1.
Соотнесите правильный ответ с предложенным:.
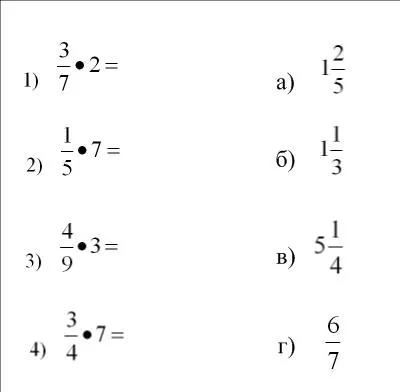
В интерактивной таблице каждый пример должен «соответствовать» правильному ответу.
Как должен быть написан ответ? Какой ответ?
Ответы должны быть записаны в виде обычных непереместимых дробей или смешанных чисел.
Правила диффузии дробей с натуральными числами и дробями были добавлены и удалены, и вычисление дробей началось с их удаления. Логично, что если вы продолжаете сотрудничать с обыкновенными дробями, то следующая проблема: ……
деление обычных пропорций на натуральные числа.
Чего вы должны достичь на наших уроках при изучении этой темы? Что вы думаете?
Учащиеся научатся делить дроби на натуральные числа.
Цели курса. Как вы будете их достигать? Что вам нужно сделать, чтобы достичь этих целей?
Рассмотрите правила деления дробей на натуральные числа, научитесь использовать их для решения различных примеров и не забывайте записывать ответы в виде несокращающихся дробей или смешанных чисел.
Фактически, это составляет цель и обязанность урока.
Сделайте вывод о правиле деления дробей на натуральные числа и попробуйте догадаться о решении следующей задачи.
‘Мать покупает ленты, чтобы украсить платья двух своих дочерей. Сколько лент ей нужно для платья, если для каждой нужно одинаковое количество?».
Правильно. Если 1 м ленты разделить на 15 равных частей, 14 из которых делятся поровну, то каждая девочка имеет 7 из 15 частей 1 м, т.е. m
(Записать в интерактивную таблицу).
Как были получены ответы из этого раздела?
Дробный числитель делится на натуральное число, но знаменатель остается прежним.
Что же произойдет, если дробный числитель не делится на целые числа? Например.
Вспомните основные свойства дробей и замените дроби равными дробями, но только теми дробями, числители которых делятся на натуральные числа. Назовите такие дроби.
Работают за партами, выполняя самостоятельно упражнение № 495
Через 5-6 минут предложите учащимся изменить свою работу. После выполнения второго варианта теста на компьютере студенту предлагается просмотреть самостоятельную письменную работу (экранное решение). Студенты проходят предварительное тестирование (5, 4 или 3).

Результаты упражнения заносятся в бланк оценки.
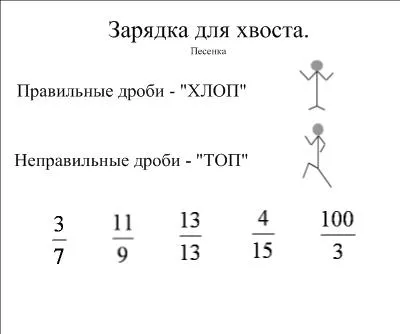
Учитель:.
Вы проделали хорошую работу и теперь можете отдохнуть, выполнив упражнение «хвост». На дисплее отображается «хвостовое упражнение».
Он объясняет, что дети аплодируют, когда на экране появляется правильный процент. Если это неправильно, их ноги идут. Звучит музыка из мультфильма, учитель показывает фрагменты, детей хвалят и подгоняют.
Проверьте, не забыли ли они правило, которое только что выучили в классе. Учитель предлагает сделать это на странице 134: 134 Контрольная работа 1, 2 и 3.
Они подходят к столу и комментируют свои ответы. Учитель комментирует их ответы.
Вы хорошо усвоили материал, но Данно нуждается в помощи. Проверьте его решения и скажите, какие правила он должен выучить лучше. На экране: ‘Help Dunno’.

Исправьте его ошибки маркером и расскажите ему о правиле деления нормальных пропорций на натуральные числа.
Подведите итоги урока. Лучшие ответы: ___________________, самый активный участник курса ____________________________.
Он пишет домашнее задание на чистом экране и комментирует его.
Студенты изучают правила на странице 133. Упражнение #503 (c, d) #504 (c, d).
Если у вас возникнут трудности, обратитесь к аналогичным упражнениям в классной работе.

Курс переподготовки
Педагогические основы деятельности учителя общеобразовательного учреждения в условиях ФГОС

Курс переподготовки
Смешанное обучение

Курс переподготовки
Развитие предметных навыков при подготовке младших школьников к олимпиадам по математике

«Домашнее обучение. Лайфхаки для родителей»
‘Дети такие разные: преимущества работы учителем’.
Сертификаты и скидки для каждого участника
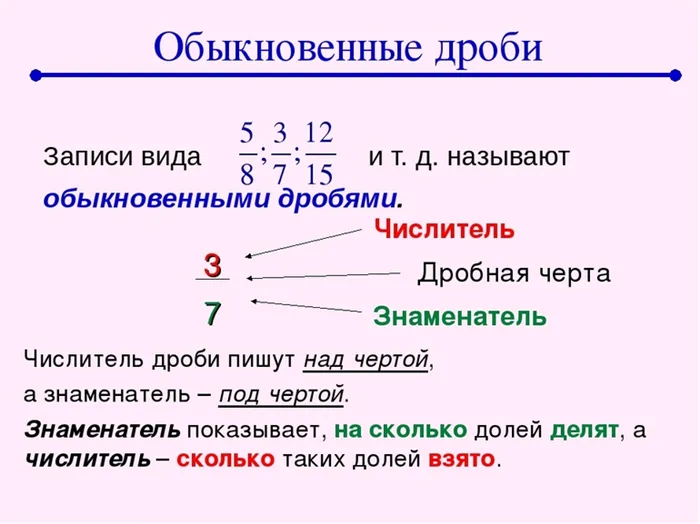
Над чертой находится числитель, делитель, а под чертой — знаменатель, делитель. Граница между числителем и знаменателем является делителем. Дети в пятом классе уже знают об этом.
Урок 18 Бесплатно Деление

В предыдущих курсах уже подробно обсуждалось поведение при сложении, абстрагировании и умножении дробей и смешанных чисел.
На этом уроке мы рассмотрим, как делить одну дробь на другую, как делить одну дробь на натуральные числа, а также разберемся со смешанными числами.
Деление дроби на натуральное число
Дроби — это, по сути, деление числителя и знаменателя, но они записываются таким образом, что воспринимаются как числа.
В этом соотношении деление дроби на натуральное число подобно делению числителя на знаменатель, а затем полученное значение снова делится на это натуральное число.
Если мы разделим яблоко на два, каждый из нас получит по ߡ (⌘ mathbf> \) яблоку.
Теперь представьте, что мы снова делим половину на три. Ясно, что одна треть половины представляет собой оригинальное яблоко \(⌘ mathbf> \).
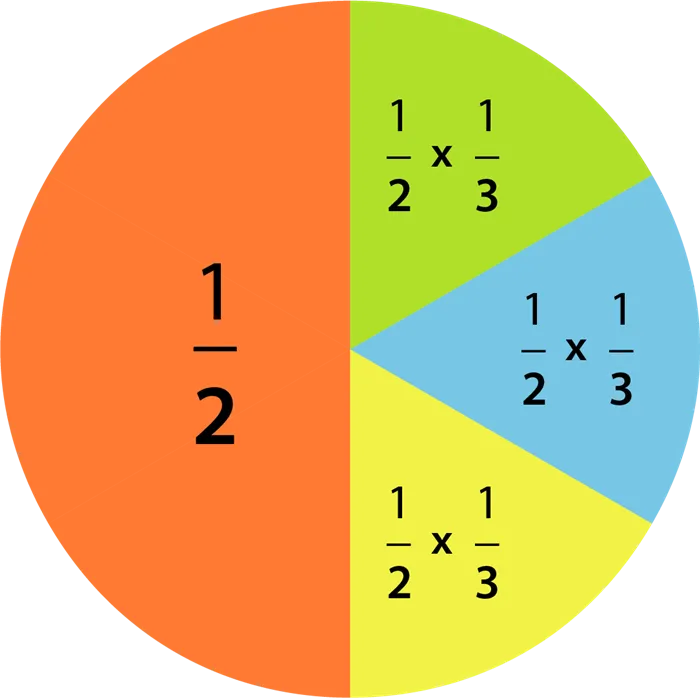
Из сказанного ясно, что если мы хотим разделить дробь на натуральное число, то результатом будет дробь с тем же числителем, а знаменатель будет произведением исходной дроби и натурального числа.
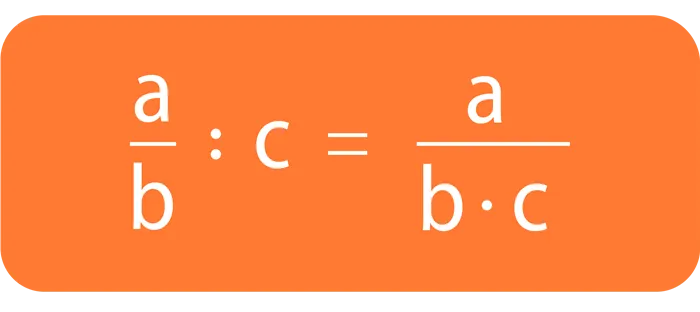
Давайте рассмотрим несколько примеров, которые помогут нам понять:.
\Деление дроби (ɑ mathbf> \) на 5.
В данном примере мы следовали правилу. Произведение исходной дроби и натурального числа записывалось в знаменатель ответа, а числитель оставался исходной дробью.
\Разделите дробь (ɑ mathbf> \) на 6.
Как видите, в процессе деления дробей появляются новые возможности.
Вы можете принять участие в викторине и получить оценку, войдя в систему или зарегистрировавшись.
Деление дроби на дробь
Мы рассмотрели простой случай деления дроби на натуральное число, которое при делении делимого имеет дело с другой дробью.
Здесь мы также можем полагаться на логику, прежде чем обратиться к окончательному правилу.
Мы определенно хотим уменьшить первое число, потому что это первое число, которое уменьшается, и мы хотим уменьшить второе число, потому что это первое число, которое уменьшается.
Поэтому, как и в случае с натуральными числами, нам нужно разделить имеющиеся дроби на числитель второго числителя.
Но затем, поскольку число слишком велико, нужно умножить результат так, чтобы вторая дробь была меньше числителя этой второй дроби.
Другими словами, исходную дробь нужно разделить на числитель второй дроби и умножить на ее знаменатель.
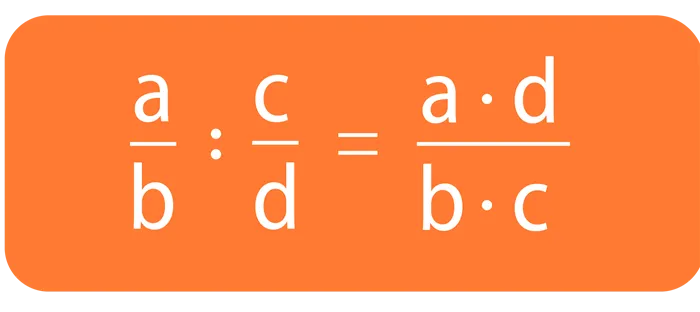
Если вы не до конца понимаете, что означает это правило и почему оно таково, не волнуйтесь, изучив примеры тестов и самостоятельных решений. Ваше понимание улучшится.
Обратите внимание, что если соответствующая дробь делится на натуральное число, то невозможно получить неправильную пропорцию, так как число уже меньше единицы.
Здесь, однако, имеет место деление с соответствующей дробью. По сути, это умножение, или увеличение, на неправильную дробь.
Таким образом, может быть задумана нерегулярная фракция. Его необходимо преобразовать в смешанное число.
В этом случае существуют также числа больше единицы, экспортируемые целые числа.
Кроме того, поскольку числитель и знаменатель записаны в виде небольших чисел, можно заметить, насколько полезно выполнять сокращение перед вычислением результата.
Также важно отметить, что деление на дробь — это фактически умножение на обратную дробь.

После записи делений вы можете смело делить дробь на два и получать именно то, что вы просили.
Вы можете принять участие в викторине и получить оценку, войдя в систему или зарегистрировавшись.
В этом соотношении деление дроби на натуральное число подобно делению числителя на знаменатель, а затем полученное значение снова делится на это натуральное число.
Деление дробных чисел
DIVIDE — это числовое действие, при котором можно узнать, сколько раз число содержится в другом числе. Деление также является обратным действием умножения.
Свойства деления: a.
Деление на единицу дает то же число. a: 1 = a. Деление на ноль дает то же число. b: 1 = a. Деление на ноль дает то же число.
При делении нуля на что-то получается ноль: 0: a = 0.
При делении числа на себя получается единица: a: a = 1.
При делении суммы на число можно сложить результат, разделив каждое наречие с ним: (a + b): c = a: c + b: C.
Если разность делится на число, то ее можно разделить на этот квантор и отнять отдельно, и отнять от второго квантора: (a — b): c = a: c — b: C.
Деление произведения двух множителей на число позволяет разделить один из множителей и умножить полученный результат на второй множитель. (c: c).
Деление обыкновенных дробей
Как разделить дробь на дробь? Выполните следующую последовательность операций.
Умножьте числитель первой дроби на знаменатель второй дроби и запишите результат в числитель новой дроби.
Умножьте знаменатель первой дроби на числитель второй дроби и запишите произведение в знаменатель новой дроби.
Другими словами, напрашивается правило: чтобы разделить одну дробь на разные дроби, умножьте первую дробь на обратную второй.
Как разделить дробь на дроби с разными знаменателями? Это просто. Используйте правило, описанное выше. На практике это объясняется тем, что нас не интересует, одинаковы ли знаменатели или нет.
Также удобнее выразить деление как обратное умножение и использовать распределительное свойство умножения по отношению к сложению, если числа достаточно большие.
Деление дробей. Правила. Примеры.
Следующей операцией, которую можно выполнить над дробями, является деление. Деление дробей довольно простое. Главное — знать некоторые правила деления. Узнайте правила деления и посмотрите пример решения задачи.
Чтобы разделить дробь на делимую дробь, нужно перевернуть делимую дробь. Это означает, что вам нужно взять обратную дробь делителя и умножить дробь на дробь делителя.
Разделите на дробь.
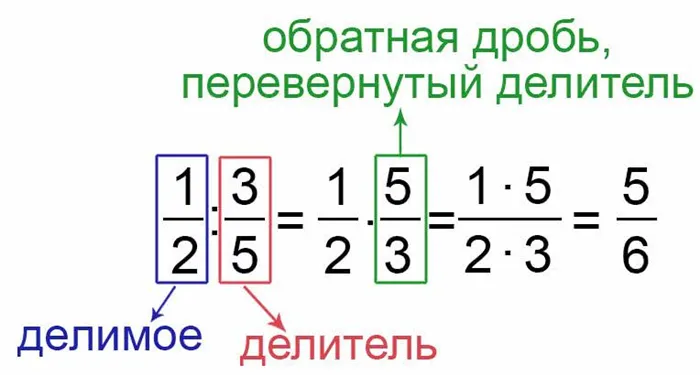
Деление числа на дробь.
Чтобы разделить число на дробь, нужно умножить знаменатель делителя на число и записать числитель делителя в знаменатель. Это означает, что дробный делитель инвертирован.
Разделите число на дробь.
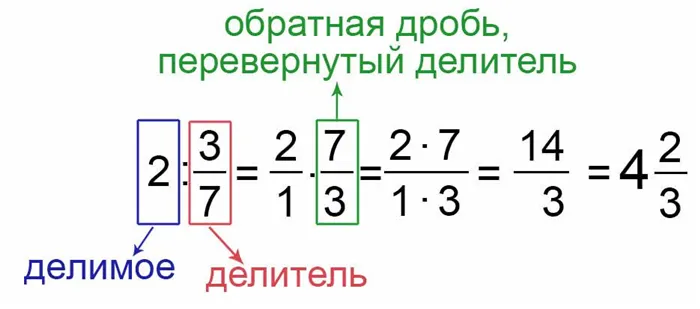
Деление числа на число.
Чтобы разделить простые числа, представьте их в виде дробей и выполните деление в соответствии с правилами деления дробей на дроби.
Примечание по делению дробей: дроби не делятся на ноль.
Похожие вопросы: как делить дроби? Как разделить дробь на дробь? ОТВЕТ: разделите дробь, разделив первую дробь на обратную делителю.
Как разделить дробь на разные знаменатели? ОТВЕТ: Все дроби, с одинаковыми или разными знаменателями, делятся по правилу деления дроби на дробь.
Пример 1: Разделите и назовите делитель. Обратные дроби делителя: a) \ (\ frac \ div \ frac \) b) \ (2 \ frac \ div 1 \ frac \)
\(⌘ frac \) — делитель, а ⌘(⌘ frac \) — обратная величина делителя.
\(⌘ frac \) — делитель, а ⌘(⌘ frac \) — обратная величина делителя.
Пример 2: Вычислить делитель: a) \(5 \ div 1 \ frac \) b) \(9 \ frac \ div 8 \)
You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.
Умножение дробей.
Добавить комментарий Отмена ответа
Вы должны войти в систему, чтобы оставить комментарий.
Свежие записи
Если вы продолжите работу над проектом, отключите блокировку рекламы или добавьте сайт в исключение блокировки рекламы.
Также удобнее выразить деление как обратное умножение и использовать распределительное свойство умножения по отношению к сложению, если числа достаточно большие.
Деление дробей
Деление дробей изучается в 5 классе математики, но материал может быть повторен в больших классах. Деление выполняется в соответствии с правилами деления дробей.
При делении дроби на дробь числитель делителя умножается на знаменатель делимого, а знаменатель делителя умножается на числитель делителя. Первое произведение является числителем, а второе — знаменателем коэффициента.
 Представление любого числа в виде дроби
Представление любого числа в виде дроби
Любое целое число можно выразить в виде дроби. Пример: ,. Теперь вы можете умножать и делить целые числа на дроби и делить дроби на целые числа.
 Операция деления
Операция деления
Для деления дробей используется простой принцип, разработанный математиками. Эта форма выглядит следующим образом.
- Записать две величины: 25/72 и 5/8.
- Указать операцию: 25/72 / 5/8.
- Перевернуть вторую дробь (поменять местами числитель и знаменатель), заменив операцию на умножение: 25/72 * 8/5.
- Произвести операцию умножения, сократив числитель и знаменатель: 5/9.
Если две величины оказываются смешанными, их необходимо преобразовать в неправильные дроби и выполнить действие деления. Дробные выражения выполняются как над известными, так и над неизвестными (переменными). Для работы с дробными выражениями необходимо знать признаки деления одного числа на другое.
Признаки делимости
В случае сокращения дробей необходимо знать точку деления. Если одно число разделить на другое, то результатом будет третье число, называемое Квотиентом. Первое число называется числом деления, а второе — делителем. Баллы дивизиона варьируются от 1 до 9 (соответствуют числовым баллам).

- Любое число.
- Последняя цифра — четная величина.
- Сумма делится на тройку.
- Две крайние справа цифры (последние) делятся на четверку.
- Последняя цифра заканчивается на нуль или пятерку.
- Сумму, полученную при сложении компонентов-цифр числа, можно делить на двойку и тройку.
- Деление по формуле mn — 2t / 7, где m, n и t — единицы, десятки и сотни искомого числа.
- Деление на двойку и четверку на основании пунктов 2 и 4.
- Алгебраическая сумма цифр, составляющих число, делится на девятку без остатка.
Пункты разделения лучше всего подготовить в виде электронной презентации или на картоне. Математик пишет мемуары. Это связано с тем, что это значительно сокращает время, затрачиваемое на примеры и решение задач.
Примеры решения
Для практического применения приобретения знаний необходимо проиллюстрировать пример деления двух величин: 4 (2/25): 2/15. дроби в этом случае разные, потому что первая смешанная, а вторая обычная. Операция выполняется по этому алгоритму.
- Преобразование 4 (2/25): (25 * 4 + 2)/25 = 102/25.
- Запись выражения: 102/25: 2/15.
- Переворот второй величины и умножение: 102/25 * 2/15.
- Сокращение 25 и 15 на 5: 5 и 3 соответственно.
- Выполнение предыдущей операции, но только для 102 и 2: 51 и 1.
- Запись искомого значения с учетом сокращений: (55 * 3) / 5 * 1 = (11 * 3) / (1 * 1) = 33.
Из этого примера видно, что деление обычного дробного выражения и другого выражения приводит к целому числу.
Поэтому при выполнении действия по делению двух обыкновенных дробей необходимо руководствоваться специальным алгоритмом, чтобы иметь возможность выяснить точки делителя и преобразовать неправильную обыкновенную дробь в правильное дробное значение.








