Дана точка m 0 (-3, 4), через нее проходит прямая и обычный вектор этой прямой n → = (1, -2). Напишите уравнения данной линии.
Уравнение прямой – виды уравнения прямой: проходящее через точку, общее, каноническое, параметрическое и т.д.
Каждая линия плоскости может быть задана первым уравнением AX + by + c = 0. Здесь A и B постоянны и в то же время не равны нулю. Такое уравнение первого класса всегда называется общим уравнением прямой линии.
Линейные уравнения — типы линейных уравнений: точечные, общие, нормальные, параметрические и т.д. Обновлено 16 апреля 2020 года: научная статья. ru
Главная / Доклады / Математика / Линейная алгебра / Линейные уравнения — типы линейных уравнений: проходящие через точку, общие, нормальные, параметрические и др.
Уравнение прямой проходящей через точку и нормальный вектор
Рассмотрим уравнение прямой, проходящей через точку и нормальный вектор. Это будет точка и ненулевой вектор в системе координат (рис. 1).
Как видите, существует только одна прямая, проходящая через точку перпендикулярно направлению вектора (в данном случае она называется нормальным вектором прямых).
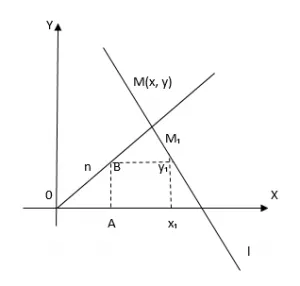
Докажем, что это линейное уравнение
Это уравнение линии. Это означает, что координаты точек каждой прямой удовлетворяют уравнению (1), но нет координат точек, которые не входят в уравнение (1).
Чтобы доказать это, заметим, что пошаговое произведение векторов имеет форму координат.
Далее мы используем очевидное свойство линий. Вектор является вертикальным только в том случае, если он содержит точку. Если оба вектора перпендикулярны, то их grad-произведение (2) преобразуется только для и только для всех их точек. Таким образом, уравнение (1) является прямым уравнением.
Уравнение (1) называется уравнением прямой, проходящей через точки, заданные обычным вектором =.
Нужна помощь в написании задания?
Мы являемся биржей профессиональных писателей (профессоров университетов и их коллег). Наша система гарантирует своевременную сдачу работы без плагиата. Бесплатное редактирование.
Общее уравнение прямой
— Общее уравнение прямой линии.
Таким образом, прямая линия находится по линейному уравнению вида (3). Напротив, прямая линия может быть построена для определенных уравнений вида (3), где хотя бы один из коэффициентов не равен нулю.
Действительно, по крайней мере, пара чисел, удовлетворяющих уравнению (3), т.е.
(Удалив последнее из (3), мы получаем вектор и отношение, определяющее линию после точки.
Каждая линия плоскости может быть задана первым уравнением AX + by + c = 0. Здесь A и B постоянны и в то же время не равны нулю. Такое уравнение первого класса всегда называется общим уравнением прямой линии.
Геометрический вывод уравнения прямой
Фактически, мы проводим линию в системе координат и записываем две точки на линии.
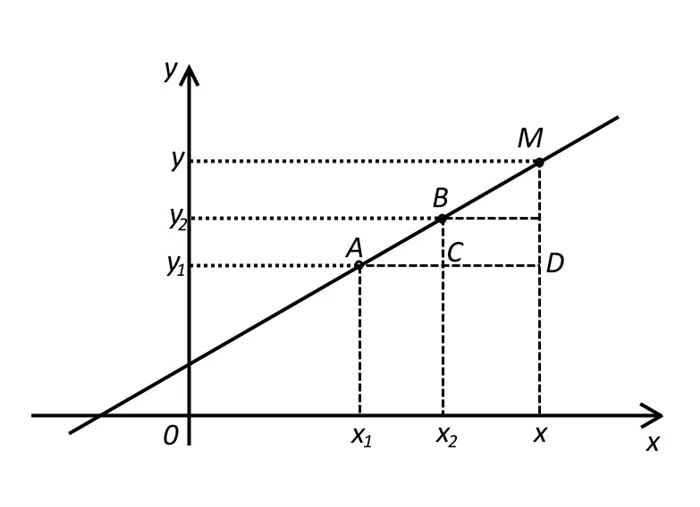
Из внешнего вида треугольника и
Таким образом, получим уравнение прямой, проведенной из двух точек.
Задача
Построим уравнение прямой, проходящей через две точки.
Решение: Проведем линию от. ,. Замените эти значения уравнением прямой, проходящей через две определенные точки.
Умножьте левую и правую части уравнения на 5, чтобы получить.
— Уравнение результирующей линии.
Проверим — правильно ли мы все решили, когда заменим координаты точек, чтобы получить верное равенство. Теперь давайте сначала заменим координаты точек.
Теперь координаты точек:.
Следовательно, уравнение линии найдено верно.
Ответ.
Условие прохождения прямой через три заданные точки
Если вам нужно проверить задачу о том, что три точки лежат на одной прямой, используя заданные координаты, вы можете рассмотреть следующее
- Если две точки с заданными координатами образуют прямую, то их координаты удовлетворяют уравнению прямой, проходящей через две точки.
- Если третья точка также лежит на этой прямой, то и ее координаты будут удовлетворять этому уравнению.
Таким образом, если три точки лежат на одной прямой, то их координаты удовлетворяют условию.
Теперь вы можете легко составить уравнение прямой из двух точек, найти угловой коэффициент прямой и посмотреть, принадлежит ли третья точка этой прямой.
Линия, изображенная на чертеже, также определяется общим уравнением 2 x + 3 y — 2 = 0, так как координаты всех точек данной линии соответствуют этому уравнению.
Уравнение прямой, проходящей через две точки на плоскости
Если даны две точки, то уравнение прямой, проходящей через эти точки, можно записать, нажав кнопку
Полученное уравнение необходимо преобразовать в общее уравнение линии.
Пример 5. Постройте общее уравнение прямой уровня, если она проходит через точку.
Решение. Тип (3).
Затем примите в преображении.
Получите общее уравнение уровня.
Пример 6.Постройте систему прямоугольников, отрегулированных на уровне линии, заданной общим уравнением.
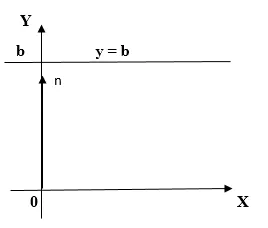
Решение. Для построения прямой достаточно знать координаты двух точек. Пересечение линии с координатами. Учитывая это уравнение, получаем, т.е. точку пересечения прямых Oy и Oy.
мы получаем, т.е. это пересечение оси волы и прямой.
Построим прямую линию, заданную этими двумя точками (см. схему слева).
Нормальный вектор этой линии является ее вектором.
Преобразование уравнения прямой с угловым коэффициентом в общее уравнение прямой
Многие задачи в аналитической геометрии требуют преобразования одного вида уравнений в другой вид уравнений. Преобразование линейных уравнений и угловых коэффициентов в общие линейные уравнения выполняется очень просто, перенося все в форму уравнения в левой части и оставляя нули в правой части. Вы получите уравнение формы.
Пример 7.Уравнение прямой с угловыми коэффициентами. Запишите уравнение линии в общем виде и в соответствии с рекомендациями для прямой линии.
Решение. Поместите все слева и оставьте нули справа.
Получили общее уравнение линии. У него Таким образом, вектор направления записывается как
Неполные уравнения прямой
Рассмотрим особенности линейно-прямой компоновки, где те или иные коэффициенты, входящие в общее уравнение линии, равны нулю.
1. если уравнение определяет прямую линию, проходящую через принцип координат, так как координаты точек удовлетворяют этому уравнению.
2.Уравнение определяет линию, прямо параллельную оси кислоты, так как обычный вектор этой линии перпендикулярен оси КРС. Аналогично, уравнение определяет прямые, параллельные оси КРС.
3.Уравнение определяет кислотную ось. Это происходит потому, что эта линия параллельна оси КРС и проходит через первую. Аналогично, уравнение определяет ось OY.
Пример 8. Постройте прямую линию в прямоугольной системе координат, заданную общим уравнением.
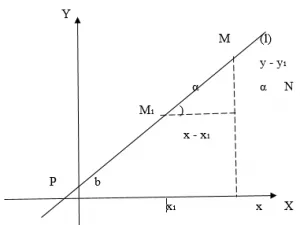
Решение. Свободный член в этом уравнении равен нулю и поэтому определяет прямую линию, проходящую через первую. Таким образом, прямая пересекает обе оси координат в точке. Чтобы построить линию, необходимо знать различные точки линии. Для этого, например, задайте произвольное значение одной из переменных в данном уравнении и найдите соответствующее значение x. Затем постройте прямую линию, проходящую через начало и точку (левая буква).
Теперь вы можете легко составить уравнение прямой из двух точек, найти угловой коэффициент прямой и посмотреть, принадлежит ли третья точка этой прямой.
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как вы знаете, существуют различные типы уравнений для одной и той же линии на плоскости. Выбор типа уравнения зависит от условий задачи. Вы можете выбрать тот, который наиболее удобен для решения проблемы. Именно здесь пригодится возможность преобразования одного типа уравнения в другой.
Сначала рассмотрим преобразование общего уравнения вида A x + B y + C=0 в обычное уравнение x—x1 a x = y —y 1ay.
Если A ≠ 0, то сумма By переносится в правую часть общего уравнения. С левой стороны снимите A с кронштейна. Результат: A x + C A =—By.
Уравнение можно записать в виде следующего соотношения: x + C A —B=yA.
Если B ≠ 0, то в левой части уравнения остается только член A x, а остальное переносится в правую часть, поэтому A x =—By—C. Поместив B за пределами квадратных скобок, имеем: A x = —B y+CB.
Перепишите уравнение в виде соотношения: x —B = y +CBA.
Конечно, вам не нужно запоминать эти типы. При условии, что вы знаете алгоритм перехода от общего уравнения к обычному уравнению.
Вам дано общее уравнение для линии 3y-4 = 0. Это необходимо преобразовать в обычное уравнение.
Запишите исходное уравнение в виде 3y-4=0. Затем продолжайте в соответствии с алгоритмом. В левой части сохраните сумму -0 x? В правой части мы получаем -3 из квадратных скобок, поэтому имеем: 0 x = —3 y—43.
Запишем полученное равенство в виде соотношения: x —3 = y—430. поэтому получим уравнение в обычной форме.
Ответ: x—3 = y—430.
Чтобы преобразовать общее уравнение линии в параметрическое уравнение, сначала перейдите к нормальной форме, а затем перейдите от нормального уравнения линии к параметрическому уравнению.
Эта линия задана уравнением 2 x-5 y-1=0. Напишите параметрическое уравнение этой линии.
Перейдите от общего уравнения к нормальному уравнению.
2 x-5y-1=0⇔2x=5y+1⇔2x=5 y+15⇔x5=y+1 5 2
Далее возьмите обе части полученного нормального уравнения равными λ, а затем
x5=λy+152=λ ⇔ x=5-λy=-15 + 2-λ, λ ∈ R
Ответ.x=5-λy=-15 + 2-λ, λ ∈ R
Общее уравнение можно преобразовать в линейное уравнение с угловым коэффициентом y = k —x + b, но только если B ≠ 0. Общая сумма By остается на левой стороне для перехода, а остаток переносится на правую сторону. Получено B y =—Ax—C. Разделите обе части полученного уравнения на B. Это ненулевое значение: y =—A B x—CB.
Приведите общее уравнение прямой: 2 x + 7 y=0. Это уравнение необходимо преобразовать в уравнение с угловыми коэффициентами.
Давайте выполним необходимые действия в соответствии с алгоритмом.
2 x + 7y=0⇔7y-2x⇔y=-27 x
Ответ: y = —27x.
Из общего уравнения прямой линии очень легко вывести уравнение по частям вида x a + y b=1. Чтобы осуществить этот переход, перенесите число C в правую часть уравнения, разделите обе части полученного уравнения на —C и, наконец, перенесите коэффициент при переменной x и y в знаменатель.
A x + B y +C = 0 ⇔ Ax+By=-C ⇔ A—Cx+ B —Cy=1 ⇔ x—CA+ y —C B = 1
Общее уравнение линии x-7y + 1 2 = 0 должно быть частично преобразовано в уравнение прямой.
Перенесите 1 2 вправо: x-7 y + 12 = 0 ⇔ x-7y = —12.
Разделите обе части уравнения на -1/2: x-7 y =-1 2. 1 —1 2 x-7-1 2 y=1.
Составление общего уравнения прямой
Мы упоминали, что, используя координаты обычных векторов и координаты точек, через которые проходит прямая, можно написать общее уравнение. Такая линия определяется уравнением a(x -x 0) + b(y -y 0) = 0. В тот же момент мы разобрали соответствующий пример.
Теперь рассмотрим более сложный пример, в котором необходимо сначала определить координаты обычных векторов.
Дана прямая линия 2 x -3 y + 3 3 = 0. Мы также знаем точку m 0 (4, 1), через которую проходит данная прямая. Напишите уравнение данной линии.
При начальных условиях мы знаем, что прямые параллельны. Далее получим вектор адреса линии n → = (2, -3) как обычный вектор линии, для которого нужно написать уравнение: 2 x -3 y + 3 3 = 0. Теперь мы знаем все данные, необходимые для составления общего уравнения для линии.
a (x -x 0) + b (y -y 0) = 0 ⇔ 2 (x -4) — 3 (y -1) = 0 ⇔ 2x -3 y -5 = 0
Ответ: 2 x -3 y -5 = 0.
Указанная прямая проходит из начала перпендикулярно прямой x -2 3 = y + 4 5. Необходимо построить общее уравнение для заданной линии.
Обычный вектор указанной линии является адресным вектором линии x -2 3 = y + 4 5.
Тогда n → = (3, 5). Прямая проходит через первую из точек o (0, 0). Нарисуйте общее уравнение для этой конкретной линии.
a (x -x 0) + b (y -y 0) = 0 ⇔ 3 (x -0) + 5 (y -0) = 0 ⇔ 3 x + 5 y = 0
Эти уравнения являются параметрическими уравнениями прямой, пересекающей точку ǫ (m_ \ слева (x_; y_; z \ справа) ǫ) в направлении вектора ǫ (ǫ bar = \ слева).
Примеры задач с решением
Необходимо построить прямые, проходящие через следующие точки: a (2, 1, 1), b (3, 1, -2).
Уравнение прямой, проходящей через точку
Он имеет следующую форму.
После применения координат точек A и B к первому уравнению, мы имеем следующий вид
После некоторых преобразований мы имеем
В этом случае наличие нулей в знаменателе не указывает на нулевое деление. Параметрическое уравнение прямой линии можно записать в таком виде.
Выражая переменные x, y и z через параметр t, мы приходим к выводу, что
ОТВЕТ: нормальное уравнение прямой, проходящей через точки a (2, 1, 1) и b (3, 1, -2), записывается следующим образом.
Параметрическое уравнение прямой, проходящей через точки a (2, 1, 1), b (3, 1, -2), записывается в виде
Необходимо построить прямые, проходящие через точки a (1, 1/5, 1) и b (-2, 1/2, -2).
Уравнение прямой, пересекающей определенную точку
Это написано так:.
После замены координат точек a и b исходного вида, она имеет следующий вид
Затем можно записать уравнение линии.
Используя параметры выражения t для переменных x, y и z, возникает следующее уравнение
ОТВЕТ: обычные уравнения для точек пересечения линий A (1, 1/5, 1) и B (-2, 1/2, -2) записываются в следующем виде
Уравнения параграфа для прямых, проходящих через точки a (1, 1/5, 1) и b (-2, 1/2, -2), имеют следующий вид
Пусть координаты точки m 0 определены как x 0 и y 0. Исходные данные показывают, что x 0 = -3. Поскольку точка принадлежит данной прямой, ее координаты удовлетворяют общему уравнению этой прямой. Впоследствии справедливо равенство:.
Нормальное уравнение
- p – длина перпендикуляра, проведенного к прямой из начала координат;
- α – угол между положительными направлениями перпендикуляра и оси абсцисс.
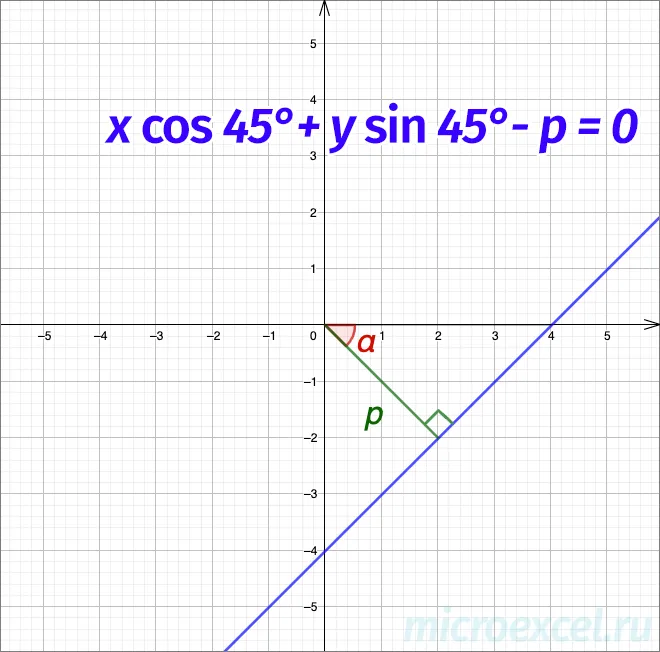
Примечание: Если p = 0, то прямая проходит через принцип координат.
- A и B не могут одновременно принимать нулевое значение;
- Если A = 0, то прямая параллельная оси абсцисс (Ox) ;
- Если B = 0, то прямая параллельная оси ординат (Oy) ;
Уравнение в отрезках и каноническое
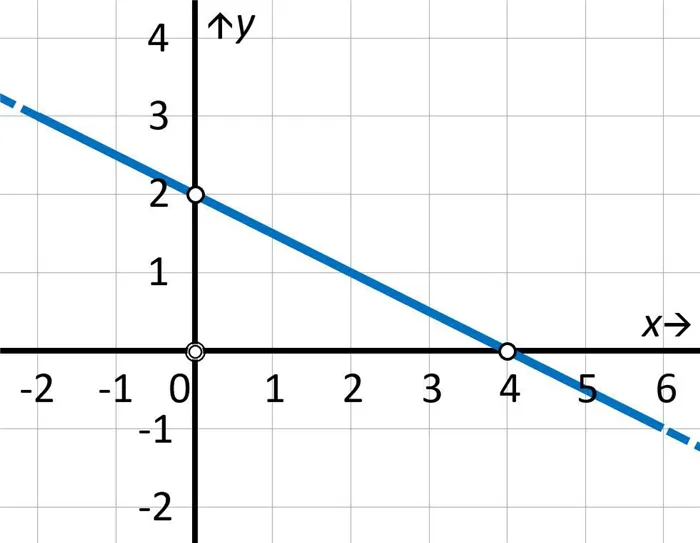
Уравнение прямого участка проще вывести из общего вида. Покажем, как это делается.
Предположим, что у нас есть следующие строки.
Переместите свободный член в правую часть уравнения, а затем разделите с ним все уравнение.
x / q + y / p = 1, где q = -c / a и p = -c / b
Существует так называемое уравнение в терминах отрезков. Он назван так потому, что знаменатель, на который делится каждая переменная, представляет собой значение координаты пересечения с соответствующей осью. Это удобно использовать для представления линии в системе координат и анализа ее связанного положения относительно других геометрических объектов (линий, точек).
Далее перейдем к экспорту регулярных уравнений. Это легко сделать при рассмотрении параметрического случая. Для случая уровня мы имеем
выразить параметр λ во всех равенствах, а затем, приравняв их, получим
Это и есть искомое уравнение, записанное в симметричной форме. Как и векторное уравнение, оно явно включает координаты направляющего вектора и координаты одной из точек, принадлежащих линии.
В этом параграфе вы можете заметить, что уравнение дано для двумерного случая. Уравнения для линий в пространстве могут быть построены аналогичным образом. Здесь следует отметить, что общее уравнение в пространстве линии появляется как система двух уравнений на уровне разреза, если символика разреза и нормальная форма представления имеют одинаковый вид.
Задача на построение уравнения прямой
Каждый ученик знает из геометрии, что простая прямая может проходить через две точки. Предположим, что следующая точка задана на уровне координат.
Вам нужно найти уравнение прямой, где обе точки являются отрезками и принадлежат вектору, нормали, общей форме.
Первым шагом является получение векторного уравнения. Для этого задайте прямой вектор M1M2¯.
Теперь вы можете составить векторное уравнение, взяв одну из двух точек, указанных в задаче. M2:.
Чтобы получить нормальное уравнение, достаточно преобразовать найденное равенство в параметрическую форму и исключить параметр L.
x = -1 -2 *λ, следовательно, λ = x + 1 /(-2), и
y = 3 +λ, и λ = y — 3.
Два других уравнения (общее и сечение) могут быть найдены из обычных уравнений путем преобразования следующим образом
Общее уравнение: x + 2 * y -5 = 0,.
Уравнение сечения: x / 5 + y / 2,5 = 1
Полученное уравнение показывает, что вектор (1; 2) должен быть перпендикулярен прямой линии. На самом деле, если вы найдете степенное произведение с вектором-драйвером, оно будет равно нулю. Уравнение прямой показывает, что линия пересекает ось x в точке (5; 0) и ось y в точке (2,5; 0).
Задача на определение точки пересечения прямых
Следующее уравнение дает две линии уровня.
Необходимо определить координаты точки пересечения этих линий.
Есть два способа решить эту проблему.
Давайте воспользуемся вторым методом. Вот:.
Это число заменяется векторным уравнением.
Таким образом, единственной точкой, принадлежащей обеим прямым, является точка с координатами (-2; 5). В этот момент линии удовлетворены.








