Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001 и т.д., отложите слева столько цифр, сколько нулей перед умножаемой единицей.
Десятичные дроби
Десятичные дроби — это дроби, представляющие собой способ представления чисел в виде символики запятой, где число до партии — целое число, а после партии — дробная часть (десятичная дробь).
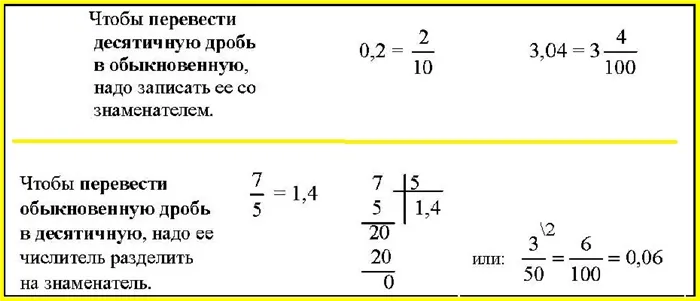
Десятичные дроби получаются в результате записи обычных дробей со знаменателями 10, 100 и 1000. Например, десятичные числа выглядят следующим образом.
4.56 — четыре целых 56 сантиметров 18.234 — 18 целых 134 миллиметра 78.6 — семь семьдесят шесть минут
Чтение десятичных цифр (десятые, сантиметры и т.д.) зависит от количества цифр после десятичной точки. Если есть цифра, то показание — одна десятая (в десятой стоит ноль, соответствующий цифре). Если после запятой стоят две цифры, он читает — сотни (100 имеет два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы добавить (удалить) две десятичные дроби в столбец:.
- Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
- Уравнять количество знаков после запятой, добавляя недостающие нулями.
- Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
- Поставить запятую под запятыми.
При сложении (удалении) целого числа и десятичной дроби после целого числа ставится запятая, а после десятичной точки — требуемое нулевое число.
Пример №1. где party находится под party и напишите соответствующий номер под соответствующим номером.
Пример №2. где запятая стоит под партией и регистрацией, где ноль прибавляется ко второму числу до нуля, равного количеству знаков после запятой.
Пример №3. Первая сумма не имеет десятичной части, поэтому откройте сторону после 56 и добавьте необходимое количество нулей.
Умножение десятичных дробей
При умножении столбца на два десятичных числа необходимо
- Написать числа одно под другим, не обращая внимания на запятую
- Выполнить умножение в столбик
- В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.
Пример нет. 4. предложения составляются так, чтобы крайние правые числа были записаны сразу друг за другом, т.е. как при обычном умножении в столбик. Распространение осуществляется без запятых. В правильном ответе первый множитель имеет три знака после запятой, второй множитель имеет один знак после запятой, а второй множитель имеет четыре числа.
0.125 x 2.3 00375 0250 0.2875
Пример №5. это распространение дробных дробей и целых чисел. Распространение осуществляется без запятых. В ответе, после партии, только первый множитель имеет десятичные части, поэтому только одна цифра отделена вправо партией, которая отделена вправо партией.
Пример №5. это распространение дробных дробей и целых чисел. Распространение осуществляется без запятых. В ответе, после партии, только первый множитель имеет десятичные части, поэтому только одна цифра отделена вправо партией, которая отделена вправо партией.
Умножение десятичных дробей: общие принципы
Сформулируйте общие принципы, которым необходимо следовать в решаемой задаче на умножение.
Помните, что изначально процесс умножения можно свести к такому же процессу для обычных дробей, поскольку десятичная точка — это просто особая форма записи обычных дробей. Это правило работает как для конечных, так и для бесконечных дробей. Это происходит потому, что после преобразования их в обычные дроби, уже исследованные правила облегчают диффузию.
Давайте посмотрим, как решаются эти проблемы.
Вычислите продукты 1, 5, 0 и 75.
Решение: сначала замените дробные дроби обычными дробями. Мы знаем, что 0, 75 равно 75 /100, а 1, 5 равно 15 10. Дробные числа можно свести к целым числам. Запишите результат как 125 1000 — 1, 125.
Ответ: 1, 125.
Как и в случае с натуральными числами, можно использовать метод измерения столбцов.
Умножьте периодическую дробь 0 (3) на другую дробь 2 (36).
Сначала измените исходную дробь на обычную дробь. Мы получаем:.
0, (3) = 0, 3 + 0, 03 + 0, 003 + 0, 003 +.. = 0, 3 1-0, 1 = 0, 3 9 = 3 9 = 1 3 2, (36) = 2 + 0, 36 + 0, 0036 +. = 2 + 0, 36 1-0, 01 = 2 + 36 99 = 2 + 4 11 = 2 4 11 = 26 11
Полученные дроби равны 0, (3)-2, (36) = 1 3-26 11 = 26 33.
Полученные дроби можно свести к десятичным дробям, разделив числитель на знаменатель столбца.
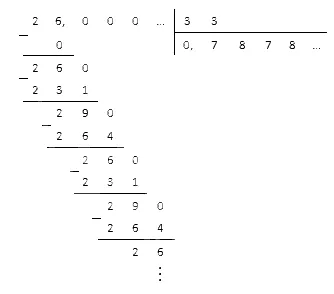
Ответ: 0, (3)-2, (36) = 0, (78).
Если в предложении задачи есть бесконечные ациклические дроби, их нужно предварительно округлить (см. статью об округлении чисел, если вы забыли, как это делается). Затем вы можете умножить уже округленную десятичную дробь на округленную дробь. Вот пример.
5, 382 … и произведение 0 и 2.
В нашей задаче мы имеем бесконечное количество процентов, которые необходимо предварительно округлить до ближайших сотых. 5, 382 … Мы обнаружили, что ≈ 5, 38. Округлять второй коэффициент до ближайшей сотой не имеет смысла. Теперь мы можем вычислить искомое произведение и записать ответ: 5, 38 — 0, 2 = 538 100-2 10 = 1 076 1000 = 1, 076.
Ответ: 5, 382 … -0, 2 ≈ 1, 076.
Как умножать десятичные дроби столбиком
Метод вычисления столбцов можно использовать не только для натуральных чисел. Если есть десятичные дроби, их можно умножить таким же образом. Возникают правила:.
Распространение десятичных чисел по столбцам происходит в два этапа.
1. игнорируйте стороны и перемножьте столбцы.
2. в итоговом числе поставьте десятичную точку и отделите с правой стороны столько чисел, сколько элементов множителя, включая десятичную точку. Если в результате не хватает чисел, добавьте нули в левую часть.
Давайте посмотрим пример такого расчета в действии.
Умножьте столбцы на десятичные числа 63, 37, 0 и 12.
Сначала мы перемножаем числа, игнорируя десятичные стороны.
Теперь мы должны поставить партии на правильные позиции. Мы выделяем четыре десятичные цифры в правой части, так как сумма десятичных цифр обоих множителей равна 4. Поскольку цифр довольно много, нет необходимости добавлять нули.
Ответ: 3, 37 — 0, 12 = 7, 6044.
Вычислите количество 3, 2601, умноженное на 0, 0254.
Подсчет без учета партий. Получены следующие цифры.
Поскольку исходная дробь имеет восемь десятичных цифр, ставится сторона, отделяющая восемь цифр от правой части. Однако это невозможно сделать без дополнительного нуля, так как результат имеет только семь цифр.
Ответ: 3, 2601-0, 0254 = 0, 08280654.
Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д
Во многих случаях на такое число необходимо умножить десятичную точку, поэтому важно, чтобы это можно было сделать быстро и точно. Напишите специальные правила, которые можно использовать для такого умножения.
Умножьте десятичное число на 0, 1, 0, 01 и т.д., и результатом будет число, похожее на исходную дробь. Партия сдвинулась влево с правильным количеством цифр. Если для переноса не хватает цифр, необходимо добавить ноль слева.
Таким образом, чтобы умножить 45, 34 на 0, 1, сторона должна переместиться на одну цифру дальше к цифре исходного числа. Наконец, есть 4, 534.
В зависимости от количества нулей партия должна быть перенесена на четыре разряда в соответствии со вторым множителем, но в первом разряде не хватает цифр. Добавьте необходимые нули и получите 9, 4-0, 0001 = 0, 00094.
Ответ: 0, 00094.
Для бесконечных десятичных дробей действуют те же правила. Так, например, 0, (18)-0, 01 = 0, 00 (18) или 94, 938 … -0, 1 = 9, 4938.
Решение: переместите партию на четыре цифры вправо. В исходной десятичной системе для этого недостаточно цифр, поэтому необходимо добавить нули. В этом случае достаточно трех нулей. Получаем 0, 02000 и 00200, 0. Игнорируя левый ноль, ответ можно записать как 200.
Умножение десятичных дробей
На этом уроке вы будете создавать идеи для умножения десятичных чисел. Ознакомьтесь с правилами умножения десятичных чисел. Особые случаи умножения десятичных чисел на 0,1, 0,01, 0,001 и т.д. будут рассмотрены. И закрепить свои знания, выполняя упражнения

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам из комплекта, вы должны приобрести их в каталоге и добавить в свой личный шкафчик.

Конспект урока «Умножение десятичных дробей»
На этом уроке мы продолжаем знакомиться с десятичными числами. Учащиеся изучат закон умножения для десятичных чисел.
Эта тема очень важна, поскольку она также используется на уроках математики в средней школе и в классах с углубленным изучением математики.
Школьный участок имеет длину 8,7 м и ширину 5,3 м. Нахождение площади школьного участка.
Нам удалось найти территорию пришкольного участка. Чтобы решить эту задачу, мы преобразовали одни значения в другие и легко нашли произведение двух натуральных чисел. Но как мы можем решить задачу, если условия задачи таковы, что нет переменных и нечего преобразовывать?
В этих случаях используются правила десятичного умножения.
Чтобы найти произведение двух десятичных дробей, используйте.:.
1) Умножьте столбцы на них как на целые числа, игнорируя запятые.
2) Затем подсчитайте количество знаков после запятой в каждом множителе и сложите значения.
3) В правой части результата разделите цифры обоих множителей на запятую.
Найдите произведение 3,143 и 1,5.

Как видите, это несложно, если следовать правилам десятичного умножения.
Если произведение содержит меньше цифр, чем количество цифр, разделенных запятыми, добавляется ноль или несколько нулей.
Найдите продукты 2,85 и 0,31.
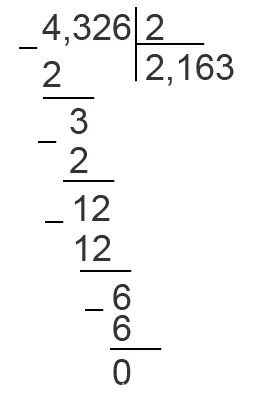
Найдите произведения 8,5 и 0,1 и 3,4 и 0,01.
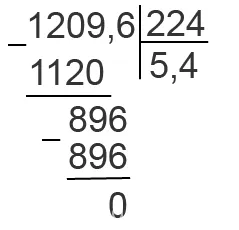
Запомните еще одно правило: 0,1 до десятичной дроби.
Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001 и т.д., отложите слева столько цифр, сколько нулей перед умножаемой единицей.
Не забывайте считать нули и целые числа!
Умножение десятичного числа на неправильное десятичное число либо увеличит его, либо оставит прежним.

Умножение десятичного числа на правильное десятичное число также уменьшит его.
Чтобы найти произведение двух десятичных чисел
1) Умножьте столбцы на них как на целые числа, игнорируя запятые.
2) Затем подсчитайте количество знаков после запятой в каждом множителе и сложите значения.
3) Разделите цифры в обоих множителях запятой справа от произведения.
Если количество цифр в произведении меньше, чем количество цифр, которые нужно разделить запятой, напишите перед ними ноль или несколько нулей.
Для умножения десятичной дроби на 0,1, 0,01, 0,001 и т.д. десятичная запятая должна быть сдвинута влево на столько же разрядов, сколько нулей перед единицей множителя.
Решение: сначала замените дробные дроби обычными дробями. Мы знаем, что 0, 75 равно 75 /100, а 1, 5 равно 15 10. Дробные числа можно свести к целым числам. Запишите результат как 125 1000 — 1, 125.
Как умножать десятичные дроби на 0,1, 0,01, 0,001
Чтобы умножить десятичную дробь на 0,1, 0,01 или 0,001, переместите сторону влево на количество цифр, равное предшествующему нулю в единице. Нулевые целые числа также учитываются. Если цифр недостаточно, добавьте один или несколько нулей после десятичной цифры.
- 34,9 ∗ 0,1 = 3,49;
- 1,8 ∗ 0,1 = 0,18;
- 145,7 ∗ 0,01 = 1,457;
- 9655,1 ∗ 0,001 = 9,6551;
- 11,9 ∗ 0,0001 = 0,00119.
Как умножить десятичную дробь на обыкновенную
Для умножения десятичных чисел с помощью обычных или смешанных дробей используются два правила. В первом случае переведите десятичную дробь в обычную дробь и умножьте на нужное число. В последнем случае преобразуйте простую или смешанную дробь в дробь, а затем перемножьте.
Пример 1. Умножьте 3/5 на 0,9.
-
Записать 0,9 в виде обыкновенной дроби:
Пример 2. Умножьте 0,18 на 3 1/4.
-
Записать 3 1/4 в виде десятичной дроби:
Домашнее задание.
Сделайте это в своем блокноте, вам не нужно его присылать!
Работа на дому — это в основном тренировка для вас!
©Copyright 2022 Урок 55. Разработано компанией Preschool and Kindergarten|Lara Theme. При поддержке WordPress.
Составьте ряд чисел от наименьшего к наибольшему. Для этого сначала разделите их на положительные и отрицательные. Затем сразу же получаем наибольшую последовательность (так как она только больше нуля) 0,021.
Свойства умножения
С дробями можно обращаться так же, как и с другими числами: складывать и вычитать, делить и умножать. В этом разделе вы узнаете, как умножать дроби.
Метафоры умножения — произведение не меняется при перестановке множителя.
Комбинаторное свойство умножения — чтобы умножить число на произведение двух чисел, нужно сначала умножить на первый множитель, а затем умножить полученное произведение на второй множитель.
Распределительное свойство умножения над сложением — чтобы умножить число на сумму, нужно умножить каждое слагаемое на это число и сложить результат.
Распределительное свойство умножения по сравнению с удалением — чтобы умножить число разностей, можно сначала умножить уменьшаемое, затем абстрагировать это число и отнять второе произведение от первого.
Умножение дробных чисел может быть упрощено простым умножением натуральных чисел. Главное — включить в ответ стороны.
Если в задаче даны десятичные числа с разными знаками — используйте правило умножения отрицательных чисел. Простой способ запомнить:.
| «−−» | минус на минус дает плюс |
| «−+» | минус на плюс дает минус |
| «+−» | плюс на минус дает минус |
| «++» | плюс на плюс дает плюс |
Числа с единицами и нулями (например, 10, 100, 1000) называются цифровыми единицами. Это связано с тем, что цифра один является единственной значащей цифрой в числе, а количественное значение числа зависит от ее расположения. Важно помнить правила умножения и деления цифровых единиц.
Чтобы умножить число на единицу числа, достаточно прибавить к нему столько нулей, сколько содержит единица числа.
Чтобы разделить число на единицу, достаточно отбросить прямо от числа столько нулей, сколько содержит единица числа.
Как умножать десятичные дроби в столбик
Умножение десятичной дроби включает в себя три этапа.
Запишите дробь в столбик и умножьте ее, как обычное число.
Подсчитайте количество десятичных цифр в каждой дроби. Добавьте цифры.
Сосчитайте возникающие числа справа налево и расположите стороны.
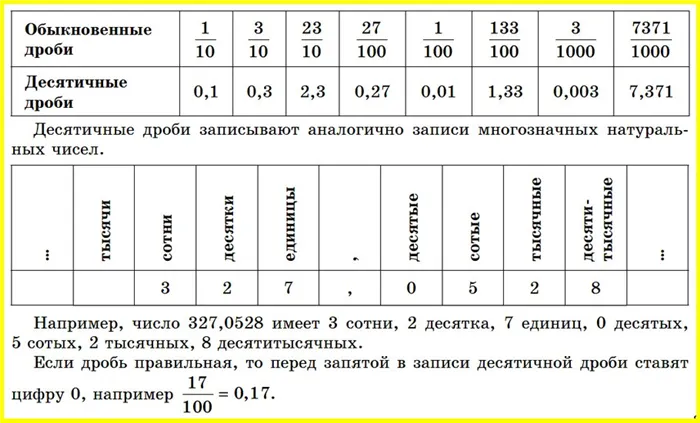
Пример: умножьте 3, 11 на 0,01.
Записывайте дроби в столбики и умножайте так, как будто сторон нет.
Измерьте общее количество чисел после партии для обеих фракций — в нашем примере их четыре (по два).
Получите число, полученное после умножения, и отсчитайте справа налево 4 цифры. Однако здесь только три цифры, а не четыре. Поэтому добавьте перед ними нули, и вуаля — четыре десятичных знака готовы.
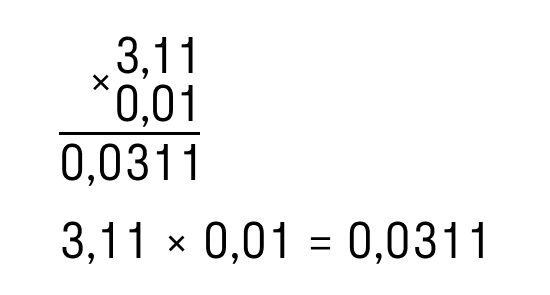
| Примеры умножения десятичных дробей столбиком: |
|---|
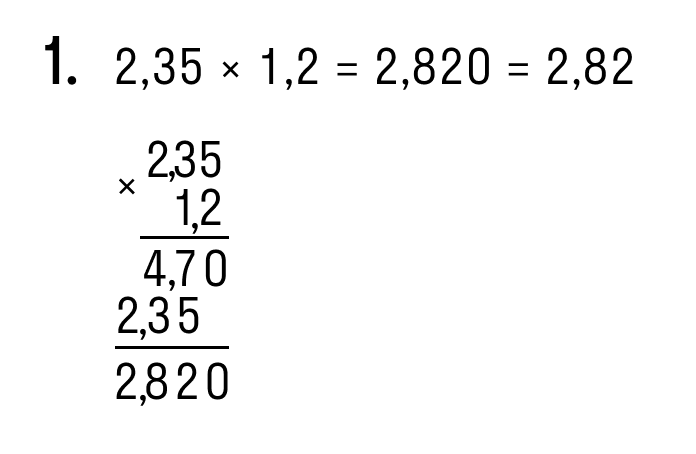 |
 |
 |
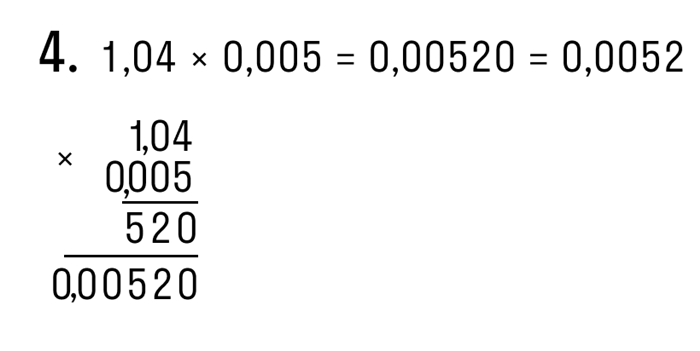 |
Как умножать десятичные дроби на натуральные числа
Умножение десятичного числа на число Хэмминга происходит так же, как и умножение десятичного числа. Чтобы считать быстрее, умножайте столбцы в соответствии с правилами, приведенными выше. Вот несколько примеров!
Пример 1. Умножьте десятичное число 2.27 на целое число 15.
Умножьте числа один на один и разделите два десятичных знака запятой.
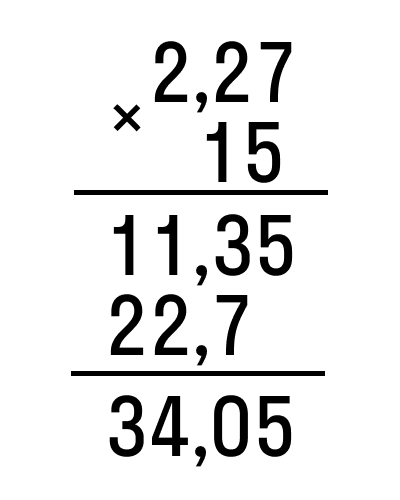
Пример 2.Умножьте 11 на 0,005.
Умножает заданное число один на один и делит на три десятичных знака.
Пример 3.0.1557… умножается на 3.
Округление бесконечных дробей:.
Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д. в этой дроби, нужно передвинуть запятую вправо на столько же цифр, сколько нулей в множителе.
Округление десятичных дробей
Десятичные числа округляются до целых чисел, десятых, сантиметров, миллиметров и т.д. Используется тот же алгоритм, но все остальные цифры не заменяются нулями, а отбрасываются, так как следуют за запятой в конце числа.
Число 86,2759 округляется до двух знаков после запятой. Количество десятичных знаков равно 2, рядом с 7. Поэтому умножьте 2 на 1.
Округлите число до миллиметра 0,372148. Число в позиции миллиметра равно 2. Следующая цифра — 1.
Округлите число 5,3721 до ближайшего целого числа. Округлите целое число до 5. рядом с 3.








