Значение. Обратная величина числа a — это число, которое при умножении на a равно 1.
Дроби. Умножение и деление дробей.
Чтобы умножить обычную дробь, умножьте числитель на числитель (чтобы получить числитель произведения) и знаменатель на знаменатель (чтобы получить знаменатель произведения).
Формула умножения дробей:.
Прежде чем приступить к умножению числителя и знаменателя, необходимо проверить, можно ли сократить дробь. Если вы сможете уменьшить дробь, расчет будет проще.
Обратите внимание! Здесь не нужно искать общие знаменатели!
Умножение дроби на натуральное число.
Обратите внимание! При умножении дроби на натуральное число числитель дроби умножается на натуральное число, а знаменатель остается прежним. Если в результате переработки продукта получается неправильная часть, всегда отделяйте целую часть, преобразуя неправильную часть в смешанную.

Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и при сложении, преобразуйте целые числа в дроби с 1 в знаменателе. Например:.
Правило умножения дробей (смешанные дроби):.
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.
Обратите внимание! Чтобы умножить одну смешанную дробь на другую, необходимо сначала преобразовать их в неправильные дроби, а затем умножить их по обычным правилам умножения дробей.
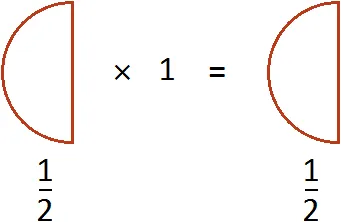
Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.
Как происходит умножение
Чтобы привить мистическую концепцию хитрого умножения, давайте определим, что это значит. Чтобы умножить число на дробь, нужно найти дробную часть целого числа.
И что мы получаем? Чтобы умножить 5 на 2/3, нужно найти 2/3 от 5.
Возникает естественный и важный вопрос. Почему, казалось бы, разные операции, такие как нахождение дробей и суммы равных чисел, описываемые в математике одним словом «умножение», выглядят по-разному?
Объяснение очень простое. Оба действия помогают решить очень похожие проблемы. Поэтому самое логичное здесь — понять и принять тот факт, что подобные проблемы могут быть решены теми же действиями и очень оправданы в реальной жизни.

Задача
Чтобы понять все это на наглядном примере, давайте рассмотрим следующую проблему. 1 кг яблок стоит 40 пенсов. Сколько будет стоить 3 кг этих яблок?».
И ежу понятно, что такую проблему можно решить, умножив количество килограммов на стоимость одного килограмма. То есть 40 * 3 = 120 рублей.
Давайте теперь попробуем понять и решить подобную проблему в несколько шагов. Давайте посчитаем: «1 кг яблок стоит 40 рублей. Какова стоимость 3/4 кг такого яблока?».
Как и в предыдущей задаче, эту задачу также можно решить, умножив стоимость одного килограмма яблок на требуемый вес.
В этой задаче можно использовать любую другую часть, независимо от того, 2/3 или 3/7, без изменения смысла и условий задачи.
Как мы видели, то же самое действие можно применить к решению проблемы, изменив только цифры, не затрагивая основополагающие понятия проблемы. Это называется умножением. Все великие вещи просты, не так ли?
Но давайте вернемся к нашему главному вопросу: умножить целое на часть. Как мы это делаем?
Давайте снова рассмотрим нашу любимую проблему с яблоками. Давайте посмотрим на приведенные там цифры.
Снова обратившись к определению, мы должны найти 3/4 от 40. Давайте начнем с чего-то более простого и найдем четверть от 40, а затем найдем 3/4.
Одна четверть от 40 (т.е. одна четверть) равна 40/4, и
3/4 от 40 — это (3 * 40)/4.
Что у нас есть:.
Рассмотрим другой случай: чему равно 40 * 5/8?
- 1 /8 от 40 это 40 /8;
- 5 /8 от 40 составляют (5*8)/40;
- В итоге получается: 40 * 5/8 = (40*5)/8 = 5*5 = 25.

Правило умножения
Давайте теперь попробуем понять правила, используемые для умножения.
- Для того чтобы умножить целое число на дробь, мы должны умножить числитель этой дроби на нужное нам значение целого числа, а потом получившийся результат поставить числителем новой дроби, а знаменатель новой дроби оставить прежним .
Если понимать эти правила с точки зрения письма, то они следующие.
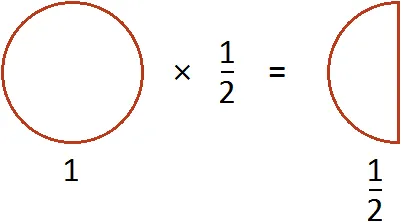
Однако важно также помнить об одном очень важном моменте. Прежде чем приступить к умножению, необходимо уменьшить то, что уменьшается, чтобы облегчить нашу жизнь. Пример: умножить 15*2/3 = (15*2)/3. Однако 15 и 3 можно уменьшить на 3, оставив (5*2)/1. Однако мы знаем, что все пропорции со знаменателем, равным 1, являются целыми и находятся в числителе. Следовательно, (5*2)/1 = 5*2 = 10. Поэтому для упрощения собственной работы рекомендуется сокращать числа.
Таким образом, вы узнали, как умножать целые числа на дроби. Надеемся, что эта статья поможет вам добиться успехов в математике. У вас широкий горизонт!
Возникает естественный и важный вопрос. Почему, казалось бы, разные операции, такие как нахождение дробей и суммы равных чисел, описываемые в математике одним словом «умножение», выглядят по-разному?

Преобразуйте смешанные числа в неправильные, перемножьте числа и знаменатели и при необходимости сократите их до смешанных дробей.
Метод 1. Умножьте числитель на натуральное число, а знаменатель оставьте без изменений. Если произведение приводит к несоответствующей дроби, следует извлечь целое число, а несоответствующую дробь преобразовать в смешанную дробь.
Метод 2.Разделите знаменатель на натуральное число и оставьте числитель без изменений.
Этот способ удобнее предыдущего, так как знаменатель делится на несимметричное натуральное число.
Решение задач
Дети 5 и 6 классов должны практиковаться в этом как можно чаще, чтобы решать такие примеры быстро и легко.
Задание 1. Выполнить умножение 2/17 на 5.
Как это сделать: умножьте числитель на натуральное число.
Задание 2. Выполнить умножение 4/15 и 55/6.
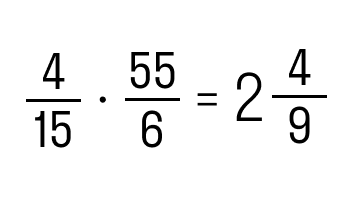
Ответ.
Задание 3. Выполнить умножение одной целой трех седьмых на шесть.
- переводим смешанное число в неправильную дробь,
- умножаем делимое на натуральное число,
- сократим полученное,
- преобразуем в смешанное число.
Математика для детей и подростков — это лучший способ понять и отработать новые задачи.
Второй способ. Сокращайте квадраты и квадраты, умноженные на знаменатель дроби. Два наибольших делителя умножаются на четыре, поэтому их можно уменьшить на четыре.
Умножение и деление обыкновенных дробей
Чтобы умножить одну дробь на другую, умножьте числитель второй дроби на числитель первой дроби (это числитель результата) и знаменатель второй дроби на знаменатель первой дроби (это знаменатель (этого) результата):.
Правило умножения нормальных дробей в типовой форме:.
Для упрощения расчетов любой молекулярный агент с любым коэффициентом знаменателя может быть приведен к общему коэффициенту перед умножением дробей.
Когда знаменатель используется для повышения решения числителя, их обычно удаляют и записывают рядом с полученным числом.
В этом примере общие делители -5 и 27 и 12 свели 25 и 20 к общему делителю -3.
Умножение дроби на натуральное число
Чтобы умножить дробь на натуральное число или наоборот, можно умножить дробную часть на это натуральное число, оставив знаменатель неизменным.
Чтобы разделить одну дробь на другую дробь, преобразуйте вторую дробь, а затем умножьте первую дробь на вторую дробь. Другими словами, числитель первой дроби умножается на знаменатель второй дроби (это произведение является числителем результата) знаменатель первой дроби умножается на числитель второй дроби (это произведение является результатом результата): знаменатель первой дроби является знаменателем второй дроби.
Чтобы проверить, правильно ли было выполнено деление, вы можете умножить полученный коэффициент на делитель и посмотреть, правильно ли вы получили делимое. Разделение было проведено правильно.
Остается только уменьшить полученную фракцию.
Правила деления обыкновенных дробей на типы:.
Иногда вы можете встретить записи в такой форме.
Поскольку вертикаль обозначает деление, эти записи могут быть переписаны в более удобном формате.
В записях, где вертикаль используется много раз, поставьте символ = перед последней вертикалью деления.
Сегодня мы изучаем только умножение целых чисел на дроби. В наши дни эта проблема имеет большое значение для всех — от биологов до математиков. Но сначала давайте поближе познакомимся с этим «чудо-зверем» — дробями.
Деление числа на дробь
Правила деления числа на дробь такие же, как и правила деления дроби на число.
Чтобы разделить число на дробь, нужно умножить обратную дробь делителя на число.
Например, разделите число 1 на .
Чтобы разделить число 1, нужно умножить число 1 на обратную дробь. Обратная дробь — это дробь.
![]()
Это выражение может быть учтено для определения количества половинок целой пиццы. Предположим, у вас есть целая пицца:.
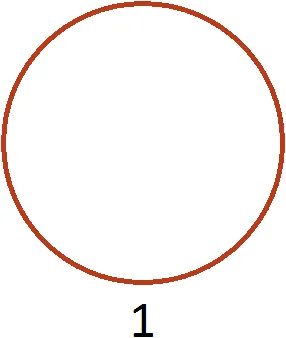
Если вопрос звучит так: «Сколько половинок у этой пиццы?». Ответ: 2. Действительно, половина дважды включается в целую пиццу.
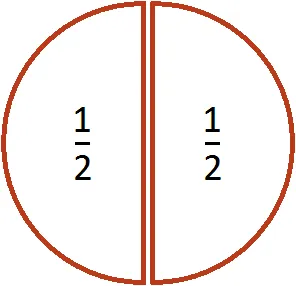
Пример 2. Найти значение выражения
Умножьте 2 на обратную величину делителя. Обратным делителем является.
![]()
Предположим, есть две целые пиццы.
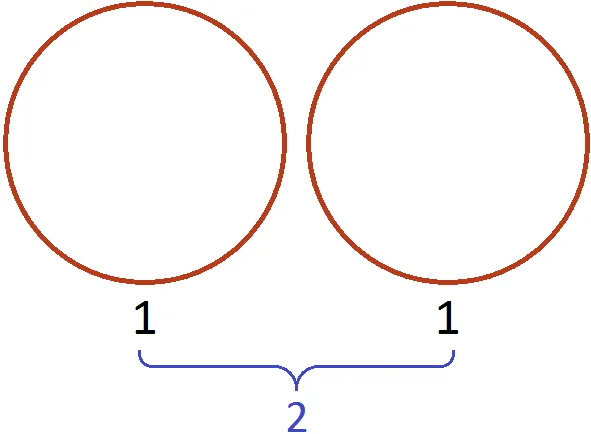
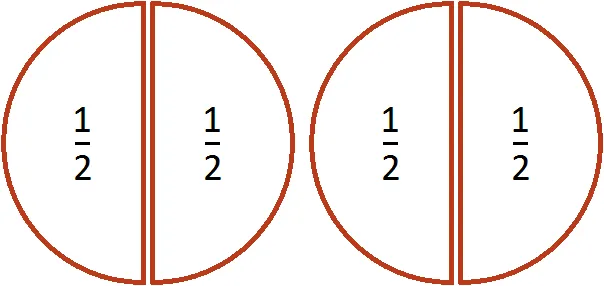
Если вопрос звучит так: «Сколько половинок в двух пиццах?». Ответ: 4. Действительно, половина этого количества содержится в двух пиццах в четыре раза.
Деление дробей
Чтобы разделить дробь на дробь, умножьте первую дробь на обратную дробь второй дроби.
Например, чтобы разделить
Чтобы разделить, нужно умножить дробь на обратную ей дробь. Обратная дробь является дробью
![]()
Предположим, у вас есть половина пиццы:.
Если мы зададим вопрос: «Сколько четвертинок пиццы в этой половинке?», то ответ будет 2. Действительно, четверть пиццы — это половина пиццы.
Пример 1. Найдите значение выражения
Умножьте первую дробь на обратную дробь второй дроби. Говоря, умножьте первую дробь на обратную часть второй дроби.
![]()
Найдите значение примера 2.
Умножьте первую дробь на обратную часть второй дроби.
![]()
Здесь вам нужно остановиться и потренироваться. Решите несколько следующих примеров. Вы можете использовать материалы этого сайта в качестве справочника. Это поможет вам научиться работать с литературой.
Объяснение очень простое. Оба действия помогают решить очень похожие проблемы. Поэтому самое логичное здесь — понять и принять тот факт, что подобные проблемы могут быть решены теми же действиями и очень оправданы в реальной жизни.
Умножение дробей
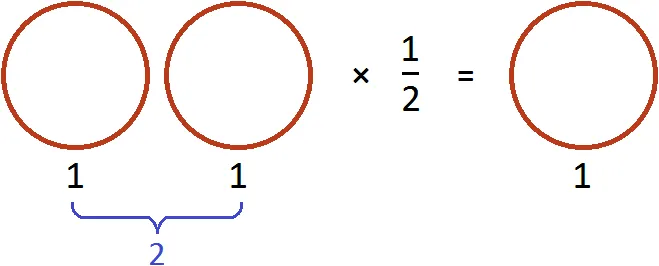
Этот урок формирует представление об умножении дробей. Вы сформулируете правила разложения дробей на числа, правила умножения дробных дробей и правила умножения смешанных чисел. Подумайте о применении этих правил при решении примеров.
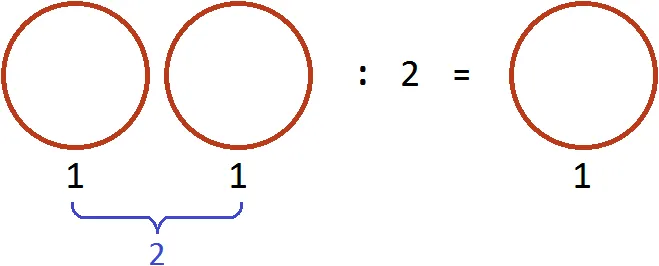
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к другим видеокурсам из пакета, вам необходимо приобрести их из списка и добавить в свой личный кабинет.
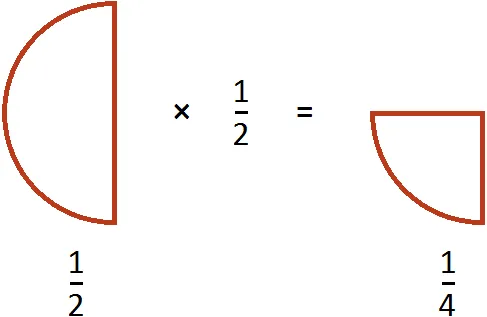
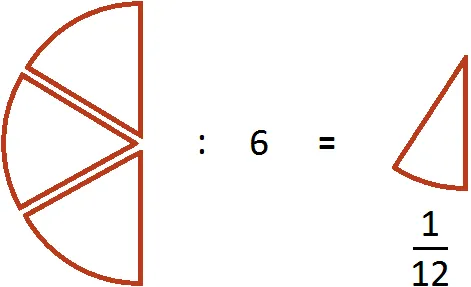
Конспект урока «Умножение дробей»
В этом уроке вы узнаете, как умножать простые дроби. Извлеките правила умножения дробей на натуральные числа, умножения дробей на обыкновенные дроби и умножения смешанных чисел.
Котёнок Васька съел на завтрак сосиски и на ужин —
Из этой символики легко понять, что числитель дроби умножается на натуральное число, а знаменатель остается прежним.
Давайте запишем правила умножения дробей на натуральные числа.
Чтобы умножить дробь на натуральное число, нужно числитель умножить на это число, а знаменатель оставить неизменным.
Это правило можно записать в алфавитном порядке следующим образом.
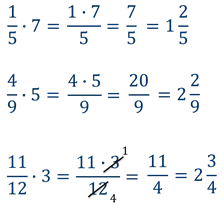
Длина прямоугольника составляет. Найдите площадь прямоугольника.
Здесь следует подвести итог общим правилам умножения дробей. Вот как получаются числитель и знаменатель Находится числитель первой дроби, умноженный на числитель второй дроби, и то же самое относится к знаменателю. Знаменатель одной дроби умножается на знаменатель второй дроби.
Таким образом, правила дробной диффузии выглядят следующим образом
Чтобы умножить дробь на дробь, числитель и знаменатель нужно умножить отдельно, причем первый результат записывается как числитель, а второй — как знаменатель.
Или короче: чтобы умножить дробь на дробь, умножьте числитель на числитель, а знаменатель на знаменатель.
Это правило можно записать в алфавитном порядке следующим образом.
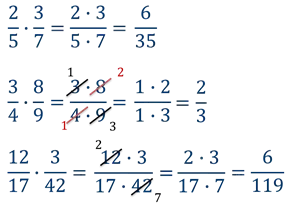
Вы узнали, как умножать дроби на натуральные числа и дроби на дроби. Осталось научиться умножать смешанные числа.
Поэтому напишите правила умножения смешанных чисел.
Чтобы перемножить смешанные дроби, необходимо сначала преобразовать их в неправильные дроби, а затем перемножить дроби.
Умножение дробей обладает свойствами мачты и комбинации, а также свойствами распределения, связанными со сложением и удалением.

Свойства нуля и единицы также применимы к распространению.

Чтобы умножить дробь на натуральное число, можно умножить числитель на это число, а знаменатель оставить без изменения.
Чтобы умножить дробь на дробь, умножьте числитель и знаменатель отдельно, записывая первый результат как числитель, а второй — как знаменатель.
Дробь — это форма представления чисел в математике. Это символизм, где a и b — числа или выражения. Существует две формы символизма.
Умножение обыкновенных дробей
В данной публикации объясняется, как можно умножить общую (исходную) пропорцию на число или другую пропорцию и как найти смешанные продукты. В нем также рассматриваются примеры стратегий решения проблем для улучшения понимания и закрепления теории.
На число
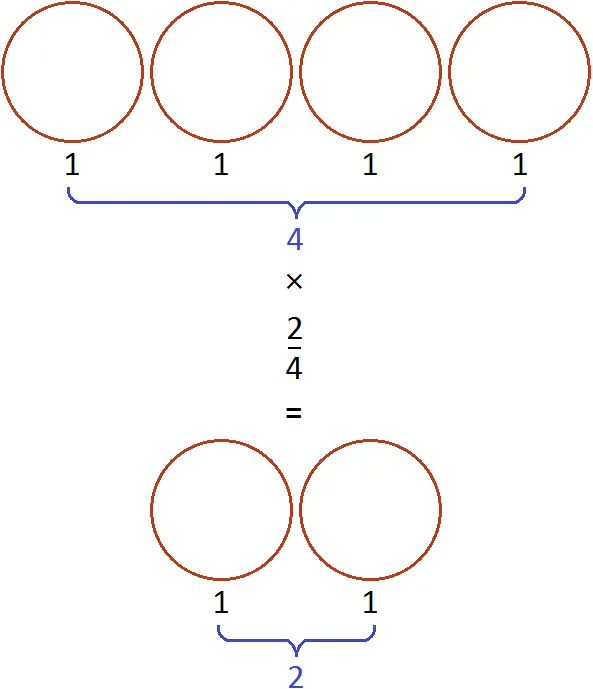
Умножение части n равно сумме составляющих n раз.
Другими словами, дробный числитель умножается на заданное число n, а знаменатель остается прежним.
Примечание: Фракцию, обусловленную пролиферацией, следует проверить, чтобы определить, можно ли ее уменьшить.
На другую дробь
Распространение между одной фракцией и другой приводит к образованию новой фракции. Ее числитель равен произведению числителя родительской дроби и знаменателя ее знаменателя.








