Угловой коэффициент линии. Прямая начинается и проходит через точку P (3; -1). В чем причина угла? y = kx+b y = kx повторение.
Уравнение прямой
Прямая GMT равна двум точкам.
(I) Общее уравнение прямой на плоскости
Уравнение прямой имеет вид $ ax + by + c = 0 $, где $ a $, $ b $ и $ c $ — некоторые числа, причем $ a $ и $ b $ не равны одновременно 0.
Если $ a = 0 $, то прямая параллельна оси ox, а если $ b = 0 $, то параллельна оси oy.
При $ c = 0 $ линия проходит через первую.
Настроенный вектор $(a; b)$ называется нормальным вектором и перпендикулярен линии.
Уравнение также можно переписать в виде $ a (x-x_0) + b (y-y_0) = 0 $.
(II) Уравнение прямой с угловым коэффициентом
Уравнения вида $ y = kx + b $ не могут определить прямую линию. Другими словами, невозможно установить прямую вертикаль на краю краевой линии.
(III) Уравнение прямой в отрезках на осях
Если прямая пересекает оси cattle и oy в точках (a, 0) и (0, b), то для уравнивания прямой можно использовать вид $ \ frac x a + \ frac = $ 1.
В этой форме невозможно представить линию через первый
(IV) Уравнение прямой, проходящей через две точки
Даны две некривые точки a (x1; y1) и b (x2; y2). Уравнение прямой, проходящей через точки a (x1; y1) и b (x2; y2), равно.
(V) Каноническое уравнение прямой
Если известны координаты $ p точек (x_0; y_0)$ на прямой, $ \ vec v = (a; b)$, то уравнение прямой можно записать в обычной форме по следующему типу.
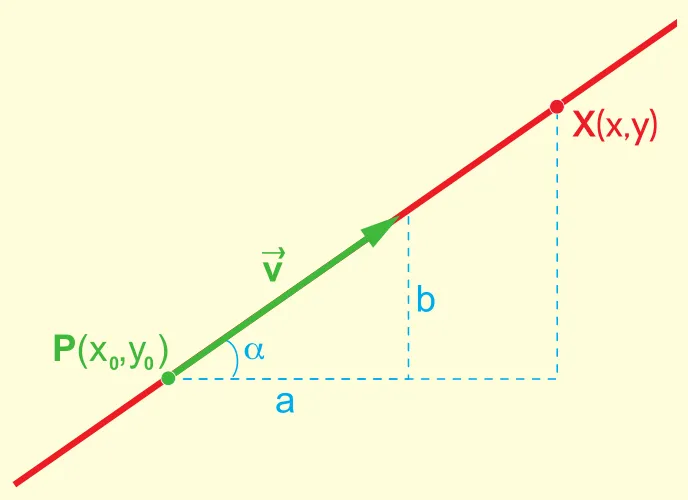
(VI) Параметрическое уравнение прямой
Уравнение парадигмы прямой можно записать в виде $ x = a t + x_0, y = b t + y_0 $, где $(x_0, y_0)$ — координаты точки на прямой, $(a, b)$ — координаты направляющего вектора прямой.
(VII) Уравнение прямой в полярных координатах
Уравнение прямой с углом наклона $ \ альфа $ к полярным координатам $ r $ и $ \ фи $: $ r \ cos(ʔ фи- \ альфа) = p $
Калькулятор
Калькулятор линейных уравнений — показывает решение
Угловой коэффициент прямой
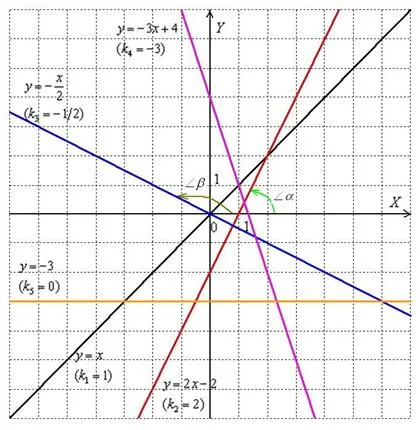
Угловой коэффициент прямой линии $ k $ = численно равен тангенсу угла между прямым и положительным направлениями оси краевой линии.
Тангенс угла может быть рассчитан как отношение соседних противоположных катетов.
Склон — крутые метры склона, холма или горы.
Чтобы найти тренд между двумя точками типа уровень 1, используйте
Горизонтальные изменения иногда называют «пробегами», а вертикальные — «подъемами» или «спадами».
Тренд первой дихотомии угловых координат равен 1, потому что скорость изменения по оси x такая же, как скорость изменения по оси y.
Например, давайте найдем наклон между (2, 1) и (-9, 7)
(Найдите градиент между (-1, -3) и (1, 1)
Чем больше шкала чисел, тем круче градиент. Положительные числа означают, что движение слева направо увеличивает градиент (линия увеличивается). Отрицательные числа означают, что движение слева направо уменьшает градиент (линия уменьшается).
Угол между двумя прямыми
Предположим, что две не сходящиеся прямые представлены уравнением $ y = a_1 x+ b_1 \\\ y = a_2 x+ b_2 $. Угол между двумя прямыми имеет вид $ tg(i) = \ frac $.
Условие параллельности двух прямых
Если угловые коэффициенты равны, то две прямые параллельны (или конгруэнтны).
Теорема. Прямые $ y = k_1 x + b_1 $ и $ y = k_2 x + b_2 $ параллельны тогда и только тогда, когда $ k_1 = k_2 $ и $ b_1 \ ne b_2 $.
Задача
Проверьте, что условие параллельности $ 3500x-3y+1 = 0 выполняется, если $ 4x-6y-5 = 0 $.
Задача
Постройте уравнение прямой, проходящей через $(1; 2)$ и сделайте $ 3500x-3y+1 = 0 $.
Условие перпендикулярности двух прямых
Условием перпендикулярности прямой является то, что произведение угловых коэффициентов равно -1 $: $ k_1 \ cdot k_2 = -1 $.
Задача
Для значений $ k $ определите выражение $ y = kx+$ 1, перпендикулярное $ y = 2x-1 $?
Задача
Постройте уравнение прямой, проходящей через $(-1; 1)$ для $ 3x-y+2 = 0 $.
Угловой коэффициент линии. Прямая начинается и проходит через точку P (3; -1). В чем причина угла? y = kx+b y = kx повторение.
Угловой коэффициент прямой
Угловой коэффициент линии — это коэффициент, описывающий степень наклона линии. Коэффициент k уравнения y = kx + b прямой в координатной плоскости численно равен тангенсу угла между положительными направлениями горизонтальной оси (совершающей наименьший поворот от оси Ox к оси O). И данная линия.
Электронный калькулятор для нахождения углового коэффициента прямой линии. Просто найдите причину угла в Интернете
- Прямая линия возрастающая, если она идет вверх с лева на право. Угловой коэффициент положителен, k >0.
- Прямая линия убывает, если она идет вниз слева направо. Угловой коэффициент отрицательный, k
- Если прямая линия горизонтальна, то угловой коэффициент равен 0
- Угловой коэффициент не существует (иногда формально говорят «обращается в бесконечность») для прямых, параллельных оси Oy .
Формула углового коэффициента прямой
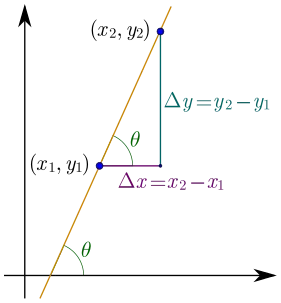
k = (Y2-Y1)/(X2-X1) (или) k = (Y1-Y2)/(X1-X2)
Предположим, что прямая проходит через две точки: p = (1, 2) и q = (13, 8). Деление разности координат y на разность координат x дает угловой коэффициент линии.
Поскольку угловой коэффициент положительный, направление линии возрастающее. Поскольку |k|
В качестве другого примера рассмотрим прямую, проходящую через точки (4, 15) и (3, 21). Угловой коэффициент равен
Поскольку угловой коэффициент отрицательный, линия уменьшается. | k |> 1, наклон линии очень крутой (наклон > 45°).
Синонимы: наклон, тангенс, наклон линии
Значение. Линия, проходящая через точку M.1 (vat.1 Вы.1 ) и перпендикуляра к y = kx+b имеет вид
Уравнение прямой, проходящей через две точки
2 Пусть M — точка M1 (vat.1, y1, z1 ) и M2 (vat.2, y2, z2 ), то уравнение прямой, проходящей через две точки:.
Если один из знаменателей равен нулю, то соответствующий числитель должен быть равен нулю. На уровне, вышеприведенное утверждение упрощается.
Дробь = k называется угловым коэффициентом.
Пример 2. Найдите уравнение прямой, проходящей через две точки A (1, 2) и B (3, 4).
Решение. Применяя вышеприведенное уравнение, получаем
Уравнение прямой по точке и угловому коэффициенту
Предположим, что мы преобразуем общее уравнение линии в плоскость Ах + W + C = 0 в следующем виде

и выразить его через угловой коэффициент k, мы получим уравнение линии.
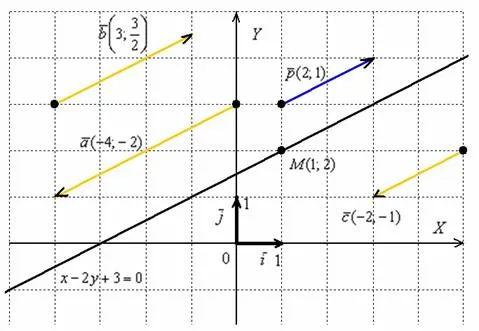
Уравнение прямой по точке и направляющему вектору
Помимо пункта об исследовании уравнения через нормальный вектор, можно ввести обозначения для прямой через точку и вектора направления.
Значение. Векторы, отличные от нуля (1, α2 ), компоненты которого удовлетворяют условию A.1 +Bα2 =0 называется направляющим вектором линии
Пример 3. Найдите уравнение прямой, проходящей через точку A (1, 2) с вектором направления (1, -1).
Решение. Рассмотрим следующую форму: Ax + By + C =0. Согласно определению, коэффициенты должны удовлетворять следующим условиям
Тогда примите вид Ax + Ay + C = 0 или x + y + C / A = 0. Для x = 1 и y = 2, C / A = -3. Это означает, что
Предположим, что прямая проходит через две точки: p = (1, 2) и q = (13, 8). Деление разности координат y на разность координат x дает угловой коэффициент линии.
Вектор нормали прямой (нормальный вектор)
Что такое норма? Проще говоря, нормаль перпендикулярна. То есть, нормальный вектор линии перпендикулярен этой линии. Очевидно, что все линии имеют свою бесконечность (и направляющие векторы), а все векторы нормальных линий склеены (сонаправлены или нет — не имеет значения).
Обрабатывать их даже проще, чем направляющие векторы.
Если линия задана общим уравнением в декартовой системе координат, то вектор является вектором этой нормали.
Если координаты вектора аккуратно «вытащить» из уравнения, то координаты нормального вектора просто «вычитаются».
Нормальные векторы всегда прямоугольные по отношению к линейному вектору направления. Используйте скалярные произведения для проверки ортогональности этих векторов.
Приведите пример с тем же уравнением, что и для векторного справочника.
Можете ли вы построить уравнение прямой линии, зная векторы точек и нормали? Инстинкт подсказывает вам, что вы можете. Если вектор нормали известен, то направление самой линии определяется однозначно. Это «жесткая структура» с углом 90 градусов.
Как составить уравнение прямой по точке и вектору нормали?
Если известны точки, принадлежащие прямой и данному перпендикулярному вектору, то уравнение прямой дается следующим образом
Здесь нет никаких дробей или других сюрпризов. Существует такой нормальный вектор. Мне это нравится. И я уважаю это =)
Составьте уравнение прямой линии из точки и нормального вектора. Найдите вектор направления прямой линии.
Решение: используйте следующее уравнение: .
Теперь, когда вы получили общее уравнение прямой, проверьте.
1) «вычесть» координаты нормального вектора из уравнения. -Да, действительно, исходный вектор возникает из состояния (или должен появиться вектор, параллельный исходному вектору).
2) Убедитесь, что точка удовлетворяет следующему уравнению.
Когда вы убедитесь, что уравнения верны, выполните вторую, более простую часть работы. Нарисуйте вектор направления прямой линии.
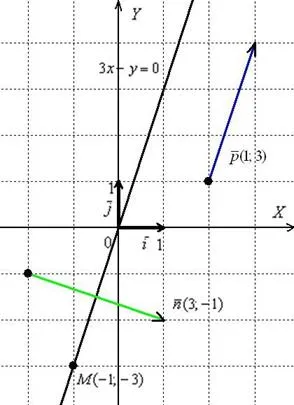
При планировании ситуация выглядит следующим образом.
В образовательных целях, аналогичная проблема, которую вы должны решить самостоятельно:.
Составьте уравнение прямой линии из точки и нормального вектора. Найдите вектор направления прямой линии.
Последний раздел курса посвящен менее распространенному, но важному типу уравнения уровня.
Уравнение прямой в отрезках. Уравнение прямой в параметрической форме
Уравнение прямой на прямом отрезке имеет вид где — ненулевая константа. Некоторые типы уравнений не могут быть выражены в такой форме. Пропорциональность прямой линии (потому что свободный член равен нулю и нет способа получить его в правой части).
Это «техническое» уравнение, образно говоря. Общая задача состоит в том, чтобы выразить общее уравнение прямой как уравнение прямой в отрезках. Насколько это полезно? Уравнение прямой линии можно использовать для быстрого нахождения точки пересечения прямой линии и координатной оси. Это очень важно для решения некоторых задач высшей математики.
Найдите точку пересечения линии с Сброс ‘hexadecimal’ приводит уравнение к следующему виду Перекресток идентифицируется автоматически.
Точка пересечения линии с осью ординат, а также ось.
Функции, подробно описанные ранее, выполняются устно.
Линия задается. Уравнение линии строится по отрезкам и определяются точки пересечения графика с координатными осями.
Решение: преобразуем уравнение в форму. Сначала переместите свободный термин вправо.
Чтобы получить единицу справа, разделите каждый член уравнения на -11.
Создайте дробь три раза.
Теперь на поверхности появится точка пересечения линии и координатной оси.
Все, что вам нужно сделать, это соединить линейку и провести прямую линию. Однако я бы предпочел снова нагрузить Excel.
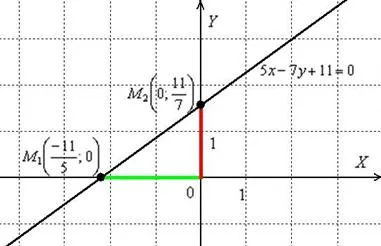
Вы можете легко увидеть, что эта линия однозначно определяется красным и зеленым участками линии. Отсюда и название «уравнение линии в отрезках».
Конечно, найти точки даже из уравнения не так уж сложно, но работа все равно полезная. Рассматриваемый алгоритм необходим для нахождения пересечения плоскости и координатных осей, приведения квадратного уравнения линии к обычному виду и других задач. Таким образом, пара независимых решений: линия
Составьте уравнение отрезка прямой в отрезках и определите его пересечение с координатными осями.
Решения и ответы в конце курса. Помните, что при необходимости все можно покрасить.
Как составить параметрические уравнениЯ прямой?
Параметрические уравнения прямой линии более важны для прямой линии в пространстве, без них контур изолирован.
Если известна прямая линия и точки, принадлежащие направляющему вектору этой линии, то параметрические уравнения этой линии задаются следующей системой
Параметрически определенные функции уже были описаны в статье Производные неявных и параметрически определенных функций. Однако мы немного повторим его в следующем демонстрационном выпуске.
Составьте параметрическое уравнение для прямой, проходящей через точку и направляющий вектор
Решение заканчивается, не успев начаться.
Параметр «te» может принимать любое значение от «минус бесконечности» до «плюс бесконечности», и каждое значение параметра соответствует определенной точке уровня. Например, возьмем пункт для.
Обратная задача: Как проверить, принадлежит ли точка в условии заданной прямой?
Замените координаты точки в параметрическом уравнении.
Если известно соотношение между точкой, принадлежащей прямой, и углом этой прямой, то уравнение этой прямой выражается следующим уравнением
Уравнение прямой с угловым коэффициентом
Предположим, что в плоскости xOy есть прямая, не параллельная оси Oy. Угол между линией и осью Ox — это угол между линией и положительным направлением оси верхней полусферы (на схеме ниже линия обозначена красным цветом).

Если линия параллельна или совпадает с осью, угол считается равным нулю.
Для составления уравнения прямой требуется только одна точка на этой прямой и угол наклона прямой по отношению к оси Ox.
Угловой коэффициент прямой линии равен тангенсу угла наклона этой линии к оси Ox.
В случае нашей задачи уравнение линии с угловым коэффициентом записывается в следующем виде
где — координаты точки, — угловой коэффициент прямой.
После подстановки вышеуказанных значений в уравнение, вы должны получить уравнение следующего вида
Пример 1.Если угловой коэффициент и линия проходят через, то угловой коэффициент используется для составления уравнения линии.
Решение. Используя уравнение (1), можно получить следующее уравнение
(2), вы получите уравнение (2).
Подстановка координат точки в уравнение и проверка показывает, что в данном случае уравнение верно.
Пример 2. Если прямая имеет угол наклона и через нее проходит прямая, то уравнение прямой записывается в терминах угловых коэффициентов.
Решение. Найдите угловой коэффициент, т.е. тангенс угла наклона прямой.
Используя уравнение (1), получаем
(2), вы получите уравнение (2).
Подстановка координат точки в уравнение и проверка показывает, что в данном случае уравнение верно.
При решении проблем тестирования проведите тест (самостоятельно), даже если проблемная ситуация этого не требует.
Из возможности контроля истинного уравнения, как показано в примерах 1 и 2, можно определить, принадлежит ли прямая, заданная уравнением с угловыми коэффициентами, любой точке плоскости с заданными координатами. Проиллюстрируем это на следующем примере.
Пример 3.Определите, принадлежит ли прямая, заданная уравнением с угловыми коэффициентами, точке и.
Решение. Подставляя координаты точки в уравнение прямой, получаем
Точка принадлежит прямой, так как получено верное равенство.
Подставляя координаты точки в уравнение прямой, получаем
Точка не принадлежит прямой, потому что было получено неверное уравнение.
Прямая, проходящая через две данные точки
Применяя уравнение (1), можно легко решить следующую задачу Найдите уравнение прямой, проходящей через две заданные точки.
Для аналитической геометрии мы нашли, что угловой коэффициент искомой линии может быть вычислен по следующему виду.
Все, что нам нужно сделать, это применить этот тип.
Пример 4.Постройте уравнение прямой с угловыми коэффициентами, если она проходит через точку.
Решение. Используя вид (3), находим угловой коэффициент.
Используя уравнение (1), получаем
Таким образом, мы имеем уравнение (2).
Для этого нужно поменять координаты точек в уравнении и проверить правильность уравнения.
Прямая, проходящая через данную точку параллельно данной прямой
Для составления уравнения прямой, проходящей одновременно через определенные точки на конкретной прямой, необходимо использовать следующие условные условия линии
Для того чтобы прямая была параллельной, угловые коэффициенты должны быть равны и соответствовать друг другу.
Следовательно, задача просто трансформируется в задачу примера 1. Тип (1) должен заменить угловой коэффициент линии.
Пример 5. Постройте уравнение прямой, проходящей через точку. Она параллельна прямой, проходящей через две заданные точки.
Решение. Используйте условие параллельности прямой. Сначала определите угловое слово прямой, проходящей через точки b и c, а затем используйте это угловое слово. Найдите угловой коэффициент типа (3).
Угловой коэффициент искомой линии также равен -5.
Теперь остается только составить уравнение прямой, используя угловой коэффициент и точки, как в примере 1.
Таким образом, мы имеем уравнение (2).
Если определено, что линия перпендикулярна данной линии, задача решается аналогичным образом. Для решения задачи на перпендикулярность необходимо использовать условие перпендикулярности линии.
Для перпендикулярности двух прямых необходимо и целесообразно, чтобы угловые коэффициенты были противоположны по величине и противоположны по синусу.








