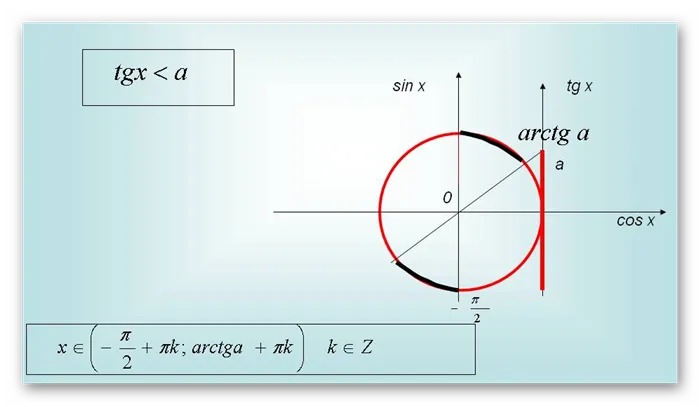
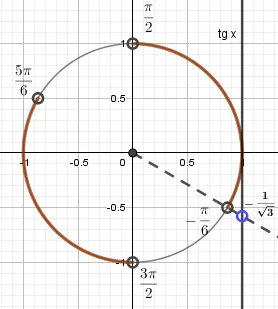
Алгоритм решения неравенства \(tgx\lt a\) будет отличаться тем, что ответом будет построение дуги из точки \(-\frac\pi2\) (где \(tgx
Простейшие и сложные тригонометрические неравенства
ightarrow -\infty\)) в точку, где была найдена дуга.
Тригонометрические неравенства Неравенства — это отношения вида a ‘ b, где a и b — выражения, содержащие хотя бы одну переменную. Неравенства могут быть строго — ‘, ‘ и не строго — ≥, ≤. тригонометрическими функциями.
Простейшие тригонометрические неравенства
являются выражениями вида: F(x) ‘ a, F(x) ‘ a, F(x) ≤ a, F(x) ≥ a, где F(x) представлен одним или несколькими тригонометрического неравенства Пример простейшего
Способ 1 — Решение неравенств с помощью построения графика функции
является: sin x ‘ 1/2. Обычно такие задачи решают графически, и для этого разработаны два метода. неравенство Найти интервал, удовлетворяющий следующему условию
- На координатной оси построить синусоиду y = sin x.
- На той же оси начертить график числового аргумента неравенства, т. е. прямую, проходящую через точку ½ ординаты ОY.
- Отметить точки пересечения двух графиков.
- Заштриховать отрезок являющийся, решением примера.
sin x ‘ 1/2, действуйте следующим образом:
Если выражение содержит строгие символы, то точки пересечения не являются решениями. Поскольку наименьший положительный период синуса равен 2π, запишите ответ следующим образом: неравенства:
Способ 2 — Решение тригонометрических неравенств с помощью единичной окружности
Если знаки в выражении не являются строгими, то интервал решения должен быть заключен в квадратные скобки -. Решение задачи также можно записать следующим образом. тригонометрического Подобные проблемы можно легко решить с помощью
- Сначала стоит начертить единичную окружность.
- Затем нужно отметить значение аркфункции аргумента правой части неравенства на дуге круга.
- Нужно провести прямую проходящую через значение аркфункции параллельно оси абсциссы (ОХ).
- После останется только выделить дугу окружности, являющуюся множеством решений тригонометрического неравенства.
- Записать ответ в требуемой форме.
круга. Алгоритм поиска ответов очень прост: неравенства Мы показываем шаги решения на примере
Решим пример с sin x ‘ 1/2. Точки a и b отмечены на окружности неравенства.
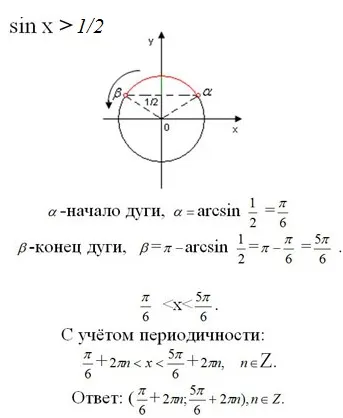
Точки дуги над a и b являются интервалом решения данной задачи
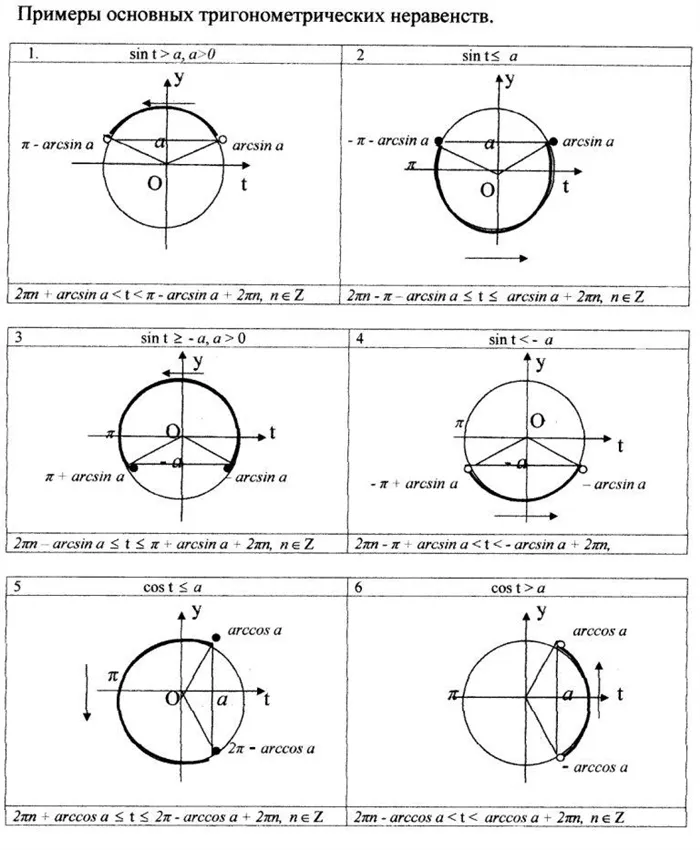
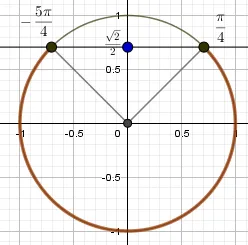
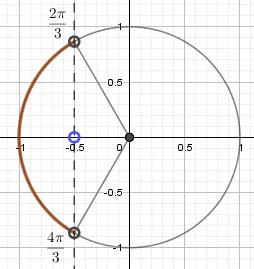
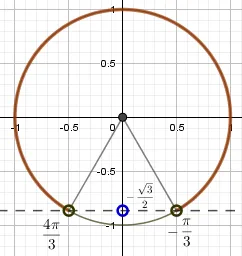
Графические решения для неравенств Если вам нужно решить пример для cos, то дуга ответов будет симметрична относительно оси OX, а не относительно оси OY. Рассмотрите разницу между интервалами решений для sin и cos на следующих графиках.
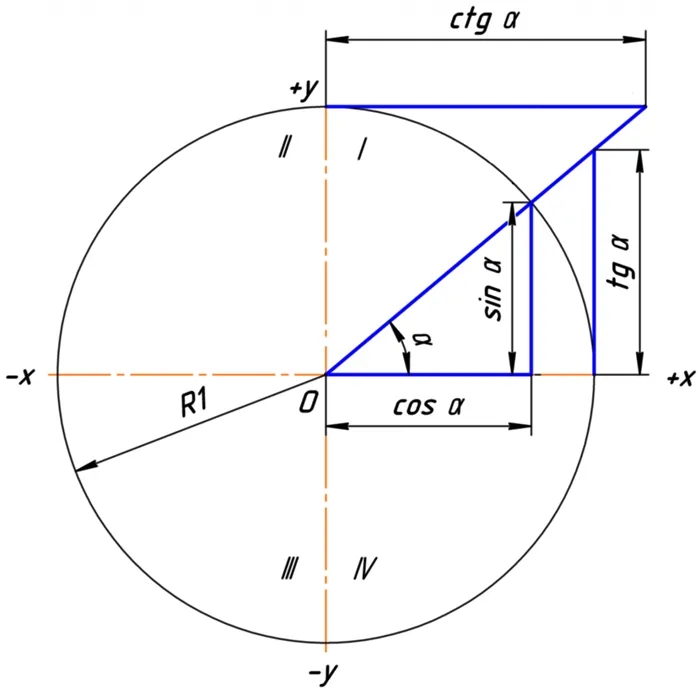
Тангенс и котангенс отличаются от синуса и косинуса. Это связано со свойствами функций. к тригонометрической Тангенс дуги и котангенс дуги являются касательными
круги, а минимальный положительный период для обеих функций равен π. Чтобы быстро и правильно применить второй метод, необходимо запомнить, на какой из осей откладываются значения sin, cos, tg и ctg.
Сложные тригонометрические неравенства
Касательная линия параллельна оси OY. Если построить значение arctg a на единичной окружности, то вторая искомая точка находится на диагональной четверти. Угол неравенства Если аргумент функции неравенстве. не простая переменная, а целочисленное выражение, содержащее неизвестное, то мы уже имеем сложную переменную неравенства:
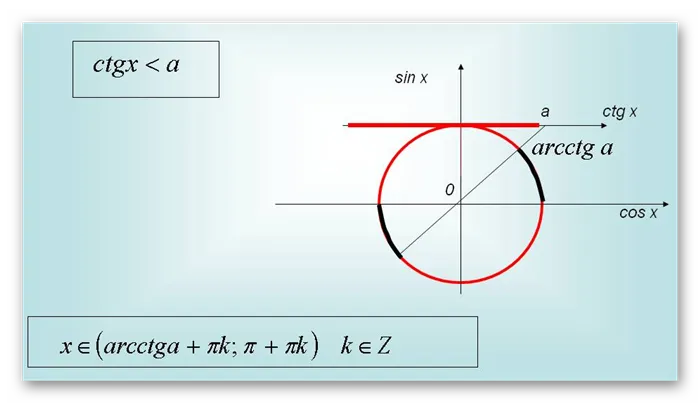
Процедура и порядок решения несколько отличаются от описанных выше методов. Предположим, нам нужно найти решение следующей задачи.
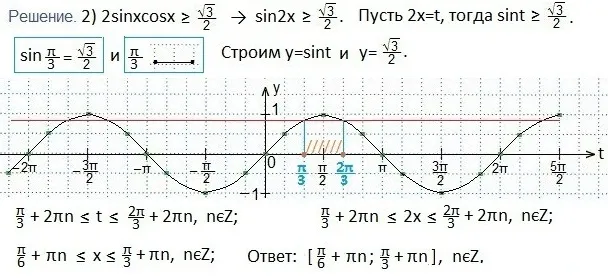
Графическое решение заключается в построении графика нормального синуса y = sin x при произвольно выбранных значениях x. Рассчитаем таблицу координат для опорных точек графика:
![]()
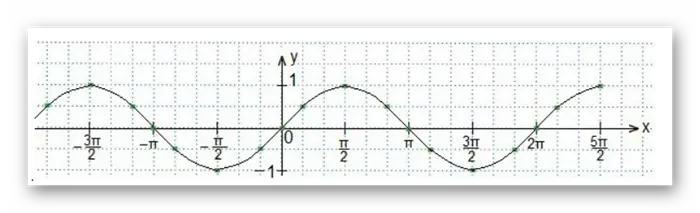
![]()
Чтобы упростить поиск решения, мы заменяем комплексный аргумент функции неравенства.
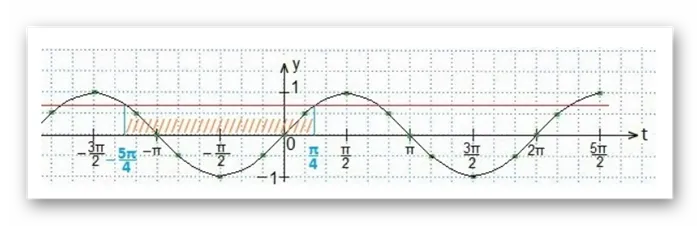
Из пересечения двух графиков можно найти диапазон необходимых значений, при которых условие
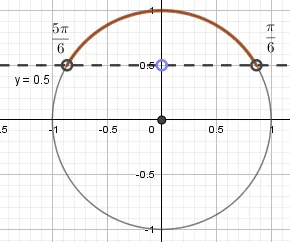
Найденная нами часть является решением для переменной t:
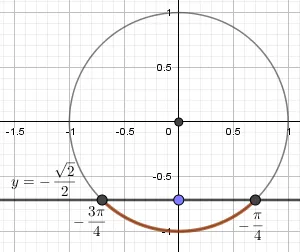
Решить двойное неравенство Однако цель задачи — найти все возможные варианты неизвестного x:

достаточно просто, достаточно переместить p/3 в крайние части уравнения и выполнить необходимые вычисления: неравенства:
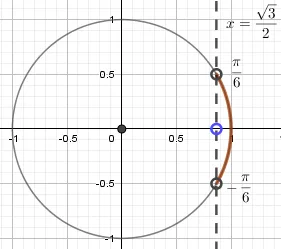
Ответ к задаче выглядит как интервал для строгой с тригонометрическими Подобные задания требуют от студентов опыта и навыков работы с
Такие задачи требуют навыков и опыта в использовании и обращении с функциями. Чем больше практических заданий решено при подготовке, тем легче и быстрее ученик найдет ответ на тестовый вопрос ЕГЭ. тригонометрических неравенств, Итак, прежде чем начать работать над методами и способами решения проблем со студентами, мы должны посмотреть. алгоритм решения простейших тригонометрических неравенств.
Тригонометрические неравенства презентация к уроку по алгебре (10 класс)
Практика и закрепление. тригонометрических неравенств» и «Решение тригонометрических уравнений» в 10 классе.
| Эти презентации были разработаны для курса «Решение элементарных задач». | Вложение |
|---|---|
| Размер | trigonometricheski_neravenstva.pptx |
| 548.04 KB | Profile_reshenie_trigonometricheskih_uravneniy_s_otbor_korney.pptx |
735.41 KB
Улучшайте свои оценки и знания с Профессором Учи.ру
Ваш ребенок потерял знания и получил плохие оценки за лето? Нет проблем! Опытные учителя помогут им вспомнить то, что они забыли, и лучше понять учебную программу. Зайдите на сайт и запишитесь на бесплатный пробный урок с преподавателем.
Предварительный просмотр:
Подписи к слайдам:
Решение тригонометрических неравенств 10 класс Бесплатный вводный онлайн-урок, 30 минут
Репетитор по математике О. Скалыга
Уравнения вида sinx sinx sinx sinx sinx sinx sinx 1) sinx 2) sinx x — любое число Нет решений.
Уравнения вида sinx sinx sinx sinx sinx sinx sinx 1) sinx 2) sinx x — любое число Нет решений.
3) sinx ОТВЕТ: +2 +2, в Z
3) sinx ОТВЕТ: — +2 +2 +2 +2, в Z
3) sinx — ОТВЕТ: — +2 — +2, в Z
Неравенство вида cosx cosx cosx cosx cosx cosx 1) cosx x любое число 2) c нет решения
3) cosx ОТВЕТ: — +2 +2 +2, к Z
cosx 2 = ОТВЕТ: +2+2+2+2+2
cosx — = ОТВЕТ: +2 +2 +2 +2 +2
Решить неравенство 3) cos ( ОТВЕТ: — +2 +2 +2, до Z — — — -.
Предварительный просмотр:
Решение тригонометрических 4 Приведите переменную cosx =t, -1 4 -8t+3 4(t- )(t- ) + — + -1 1 — +2 +2 +2, к Z.
Уравнения с выбором корней профильного уровня ЕГЭ Профессор математики МКОУ «Тельмановская СОШ» Скалыга О.В.
Решите уравнение: =0 2) =0 + ( =1 — ОТВЕТ.
Решите уравнение tg =. Ответ: назовите наименьший положительный корень уравнения = + = + + + + x-2= +3k x=2,5+3k k=0, x=2,5 Ответ: 2,5
Решите уравнение +2x)= РЕШЕНИЕ: 1) 2 2 =0 =0 x= + k, k неравенством
Методы отбора корней 1. по кругу 2. методом перебора 3. методом удвоения
2) = 0 ; ; 3 = ОТВЕТ: 1) X= + k, k ; x= x= 2) ; ,
Двойное неравенство Перебор k X= + k, k Z или 2,5 4 Если k =1, то x= + = Если k =2, то x= + 2 = Если k =3, то x= + 3 = Если k =1, то x= +2 = Если k =2, то x= + 4 = Если k =1, то x= +2 =
1) + k + k 2 k 3,5 k = 2;3 k = 2, x = ; k = 3, x = 2) + 2 k + 2 k k K — не целое число 2) +2 k + 2 k k k k k = 1, x =
a)Решите уравнение 2 b)Найдите все корни этого уравнения, принадлежащие разделу РЕШЕНИЕ: a)2 2 ( )= 2( + )= 2( + )= =0 2x= + k, k Z x = + k, k Z
x= + k, k Z -5 -4 =- -4 =- =- =- ОТВЕТ: a) x= + k, k Z ; b) — ; — ; — ; -.
α) Решите уравнение 2 )-2 + б) Найдите все его корни в отрезке Решение: 2 )-2 + 2( + =0 =0 2 x -1 — — =0 2 x — =0 cosx = с osx =- Нет корней x= ± arccos (- )+2 x= ± ( )+ 2 x= ± + 2
По теме: методические разработки, презентации и конспекты
Урок алгебы в 10 классе по теме «Решение тригонометрических неравенств методом интервалов»
x= ± + 2 3 — 3 = Ответ: a) ± + 2 ; b) неравенств, содержащих тригонометрические Метод интервалов особенно эффективен при решении алгоритм решения тр.
Тригонометрические неравенства
функция. Этот урок посвящен неравенства».
Решение тригонометрических неравенств
Презентация «Тригонометрические функции».
Решение тригонометрических неравенств 10 класс ( профиль)
Методическая разработка для курса математики. тригонометрических неравенств. Данная презентация создана для того, чтобы помочь учителю разобраться с этой темой: Решение
Учебное пособие для средних школ (профиль), М.: Мнемозина, 2007.А.Г. Мордко. тригонометрических неравенств»
«Решение элементарных задач. алгорим решения простейших тригонометрических неравенств. Данная презентация показывает, как решать элементарные математические задачи. 10 классе или при.
Презентация может быть использована для изучения нового материала в контексте преподавания математики. тригонометрических неравенств»
Урок по теме «Решение класса.
Такие задачи требуют навыков и опыта в использовании и обращении с функциями. Чем больше практических заданий решено при подготовке, тем легче и быстрее ученик найдет ответ на тестовый вопрос ЕГЭ. тригонометрических неравенств, Итак, прежде чем начать работать над методами и способами решения проблем со студентами, мы должны посмотреть. алгоритм решения простейших тригонометрических неравенств.
Тригонометрические неравенства
Мы практикуем и закрепляем. тригонометрических уравнений.
Давайте сначала вспомним формулы для решения элементарных тригонометрических неравенств Для решения простейшей тригонометрическую уравнения, мы сначала должны решить соответствующее уравнение, а затем неравенства. круг, чтобы найти решение. тригонометрических неравенств на примерах.
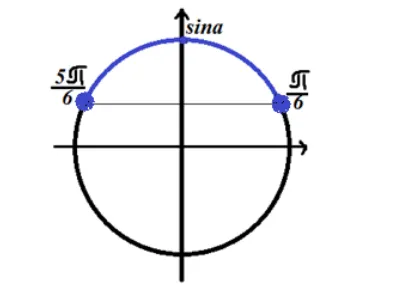
Найдем решение тригонометрического неравенства $sinx=\frac$
Отметим решение на тригонометрической окружности