Тогда центр каждого цикла равен стороне треугольника и, таким образом, совпадает с пересечением $ i $ делений треугольника, а радиус равен расстоянию от $ i $ до стороны треугольника.
Точка пересечения биссектрис треугольника

Один треугольник имеет три характерные линии: высоту, интерстицию и биссектрису. Каждая из этих линий имеет точку пересечения, которая характеризует треугольник. Первый всегда является пересечением делений. Это связано с тем, что именно эта точка дает представление о соотношении между ценой треугольника и связанной с ним окружностью.
Определение
Место встречи сторон является одной из самых проблемных точек. Это приводит к пониманию зарегистрированных и записанных форм. Это очень трудно понять. Нужно учитывать не только треугольники, но и окружности, внутриглазники и периметры. Это затрудняет решение проблемы.
Но с другой стороны, значения эндоцикла и периферийных лучей появляются во многих типах и могут упростить решение многих задач. Но сначала нужно понять, что такое акроцикл и эндоцикл. Далее необходимо узнать, как они соотносятся с пересечением разделов.
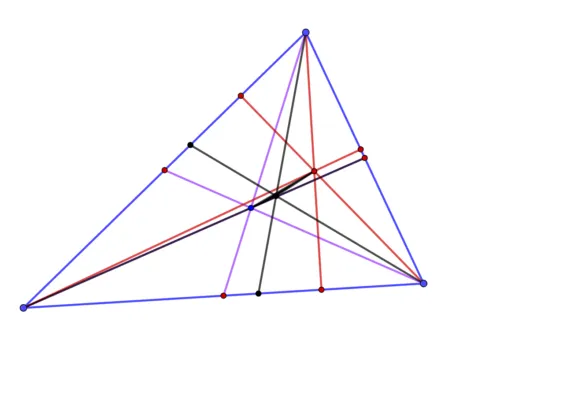
Рисунок 1.Золотой разрез в треугольнике
С произвольными остроконечными треугольниками свойства не совпадают. Соединив их вместе, вы получите золотое пересечение треугольников. Для нормальных треугольников золотым сечением является точка. Для треугольников изочель золотое сечение является прямой.
Зарегистрированные окружности — это окружности, которые касаются каждой стороны треугольника.
Центр такой окружности называется центром треугольника. Центр или пересечение треугольной тупой перегородки всегда находится в треугольнике, в отличие от высоты.
Расстояние от фокальной точки с обеих сторон одинаковое, академический радиус. Тогда треугольник считается границей.
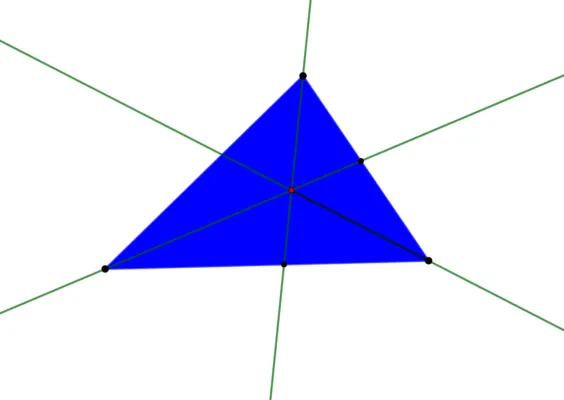
Рисунок 2.Центры треугольника.
Окружность — это окружность, касательная ко всем вершинам треугольника. Это означает, что каждая вершина должна попадать в пределы круга. И наоборот, в этом случае треугольник регистрируется, а расстояние от вершины треугольника до центра окружности всегда одинаково и равно радиусу окружности.
Теоремы о точке пересечения биссектрис
Теорема на самом деле одна, но доказательство состоит из двух частей. Заявление выглядит следующим образом. Биссектрисы треугольника пересекаются в некоторой точке, и эта точка является центром в клетке.
Сначала мы докажем, что три биссектрисы пересекаются в одной точке. Сделайте это и разделите BM, CP и AK в треугольнике ABC. O и зарегистрируйтесь на перекрестке. Далее рассмотрим каждый бисектор отдельно. Расстояние от сторон треугольников A и C должно быть равно биссектрисе AK. Для биссектрис CP расстояния C и A должны быть равны. Для BM BM расстояния C и C должны быть одинаковыми. Отрезки A, C и C равны друг другу благодаря статусу биссектрисы. Каждая геометрическая точка окклюзии равна стороне угла.
И может быть только одна точка, равная для каждой стороны. Просто установите точку пересечения в другом месте, и вскоре вы поймете, что условие не выполняется, что невозможно.
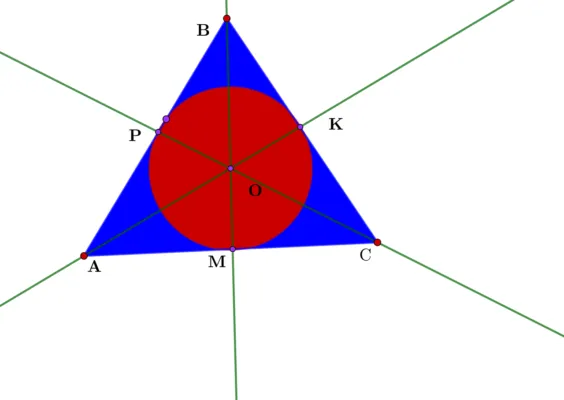
Рисунок 3. План проблемы
Мы уже упоминали, что в треугольнике только одна точка может быть равна всем сторонам. Это означает, что данная точка зарегистрирована в треугольнике, так как радиус этого цикла перпендикулярен сторонам треугольника. Теперь мы докажем, что в треугольнике зарегистрирована только одна окружность. Если перенести точку в другую часть треугольника и провести перпендикуляры к сторонам, то станет ясно, что перпендикуляры не равны друг другу, а значит, центр не может находиться в этой точке. Это то, что вы должны были доказать.
Помните анекдот: укус — это крыса, бегущая по рогам и расщепляющая рога посередине. Ну, настоящее определение укуса очень похоже на эту шутку: это треугольник.
Теорема
Стороны треугольника пересекаются в некоторой точке.
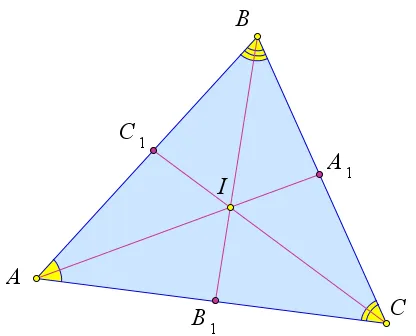
Доказательство
Первый способ.
Рассмотрим нарисованные треугольники $ aa_1 $ bbs $ bb_1 и $ cc_1 $ abc $.
Перемножая эти уравнения, получаем $ \ dfrac \ cdot \ dfrac \ cdot \ dfrac = \ dfrac \ dfrac \ dfrac \ dfrac = $ 1. Это означает, что, согласно теореме Чевы, дихотеаторы $ aa_1, bb_1 и $ cc_1 $ пересекаются. В определенный момент времени.
Второй способ.
Рассмотрим нарисованные треугольники $ aa_1 $ bbs $ bb_1 и $ cc_1 $ abc $.
Докажите, что все стороны пересекаются в один и тот же момент времени.
Предположим, что точки $ aa_1 $ и $ bb_1 $ пересекаются в точке $ i $.
Тогда Теорема $ \ rho (i; ab) = \ rho (i; ac) $ из $ i \ в aa_1 $, $ \ rho (i; ba) = \ rho (i; bc) $ из $ \ rho (i; ba) $ $ i \ в bb_1 $.
Тогда $\ rho (i; ca) = \ rho (i; cb) $ означает.
Следствие
Каждый треугольник может быть зарегистрирован в круге, центр которого является пересечением партнеров. Существуют только такие круги.
Доказательство
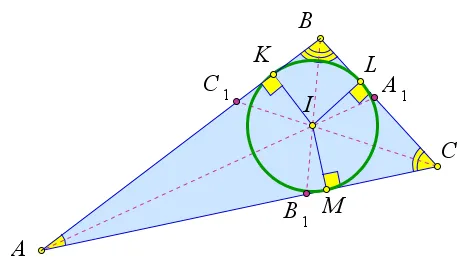
Рассмотрим любой треугольник $ abc $, обозначив пересечение его деления с $ i $.
Из этой точки проведите перпендикуляры $ ik, il $ и $ im $ к $ ab, bc $ и $ ca $ соответственно.
Так как точки $ i $ находятся на сторонах треугольника, то $ ik = il = im $.
Таким образом, центральный цикл $ i $ и луч $ ik проходят через точки $ k, l $ и $ m $.
Стороны треугольника $ abc $ перпендикулярны $ ik, il $ и $ im $ и поэтому касаются этого цикла в точках $ k, l и m $.
Таким образом, центральный цикл $ i $ и радиус $ ik $ зарегистрированы в треугольнике $ abc $.
Докажите, что существуют только такие циклы.
Действительно, предположим, что в треугольнике можно зарегистрировать два цикла.
Тогда центр каждого цикла равен стороне треугольника и, таким образом, совпадает с пересечением $ i $ делений треугольника, а радиус равен расстоянию от $ i $ до стороны треугольника.
Следовательно, эти окружности совпадают.
Следствие
Если все стороны выпуклого многоугольника пересекаются в одной точке, то можно вырезать окружность, центром которой является пересечение биссектрис.
Доказательство
Если все стороны пересекаются в точке, то эта точка равна всем сторонам, т.е. перпендикуляры к сторонам многоугольника равны, окружность с центром в этой точке и радиусом равна окружности с равным радиусом на расстоянии от точки пересечения из. Бисквиты по бокам соприкасаются со всеми сторонами.
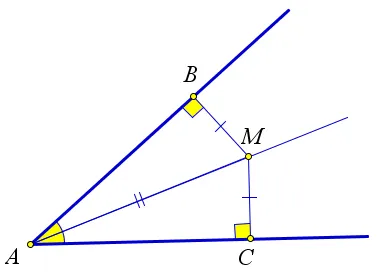
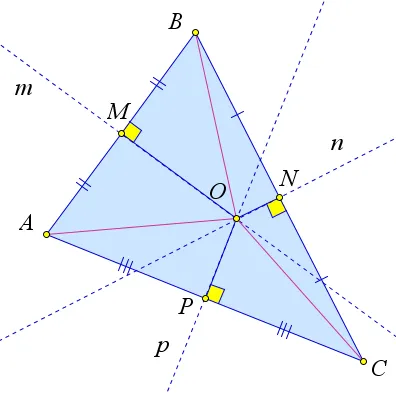
Рассмотрим треугольник $ abc $. где $ am, Ǿ bp и Ǿ ck $ — его партнеры. Пусть $ o $ o $ — точка пересечения дихотексов $ am \ и ߋ bp. Из этой точки проведите перпендикуляры к сторонам треугольника (рис. 2).
Треугольник. Элементы треугольника
Этот видеоклип посвящен треугольникам. Назовите элементы треугольника. Это также доказывает, что рассеиватели треугольника пересекаются в определенной точке, дихотеты треугольника также пересекаются в определенной точке, а высоты или линии, содержащие высоты, пересекаются в определенной точке.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеокурсам, вам необходимо приобрести их из списка и добавить в свой личный кабинет.
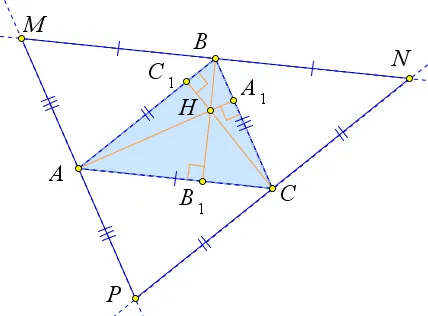
Конспект урока «Треугольник. Элементы треугольника»
— Назовите элементы треугольника, и
— Докажите, что интерстиции треугольника пересекаются в один и тот же момент времени, и
— Докажите, что окклюзии треугольников также пересекаются в одной точке, и
— Докажите, что высоты или линии, содержащие высоты, пересекаются в одной точке.
Треугольники — одна из самых удивительных и самых важных фигур геометрии.
Теперь отметьте три точки A, B и C, которые не являются одной прямой и соедините с отрезком. Полученная геометрическая фигура называется треугольником.
Очки,… это вершина и сечение треугольника, а также стороны треугольника.
Треугольник, который мы создали, называется треугольником a.
Затем они говорят «треугольник a b c».
Изменяя буквы, тот же треугольник можно обозначить как
Их углы называются углами.
Кстати, углы треугольника также можно объявить одной латинской буквой.Например.𝐵, ∠𝐵, поле.
Сумма длин всех сторон треугольника называется периметром треугольника. Другими словами, периметр нашего треугольника равен.
Различие междуТреугольник.:.
— Углы в соответствии с размером :.
Острые углы (все углы треугольника острые, т.е. меньше 90°); и
Прямоугольный (один из углов треугольника правильный, т.е. равен 90°), и
Следует помнить, что стороны прямоугольного треугольника имеют специальные названия. Таким образом, обе стороны, образующие прямой угол, называются катетами, а сторона, противоположная прямому углу, — подчиненной.
Третий вид треугольника называется тупоугольным (один из углов треугольника тупой, т.е. превышает 90°).
Затем треугольники различают в зависимости от размера сторон.
равнобедренный (все стороны разной длины), и
равнобедренный (две стороны равны и называются боковыми сторонами, третья сторона — основание), и
равнобедренный (все стороны равны друг другу).
Для каждого треугольника.Для наибольшей стороны существует наибольший угол…;Для равных сторон существуют равные углы.. Любая сторона треугольникаменьше, чем сумма иБольше, чем разница между двумя другими сторонами.
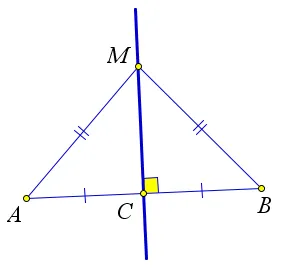
Медиана треугольника — это часть треугольника, соединяющая вершину треугольника с центром противоположной стороны.
Каждый треугольник имеет три промежуточных.Например.возьмите треугольники. В таком случае, затем идут их средства, затем отрезки, а затем — промежуточные треугольники.
Интерстициальность, взятая из вершины треугольника, и (или его длина), может символизировать следующее
Биссектриса треугольника — это часть треугольника, которая делит углы и соединяет верхние части треугольника в противоположных точках.
Каждый треугольник имеет три биссектрисы. Возьмите треугольник и начертите биссектрисы углов.
Сторона, спроектированная вершиной треугольника и (или его длиной), может быть символизирована.
Высота треугольника перпендикулярна, вписана из вершины в прямую, содержащую противоположную сторону.
Каждый треугольник имеет три высоты. Нарисуйте треугольник и отрезок. Это возвышение треугольника.
Высота, спроектированная вершиной треугольника и (или его длина) может быть объявлена как
Мы узнали о пересечении отрезков треугольника, выделили и доказали две части теоремы. Мы доказали, что в треугольнике существует только одна зарегистрированная окружность, и узнали о золотом пересечении треугольников.
Свойства и соотношения
На основе теоремы о раздвоении D было выявлено несколько важных свойств, которые рекомендуется применять при решении задач или доказательстве других утверждений.

- Центр вписанной окружности соответствует точке их пересечения.
- Точка при пересечении делит биссектрису по такому соотношению: отношение суммарного значения прилежащих к противолежащей стороне.
- Угол между биссектрисами двух смежных углов является прямым.
- В равнобедренном Δ равны только 2 биссектрисы, а в равностороннем — 3. Кроме того, она является медианой и высотой.
При решении задачи необходимо найти ее длину (L).
Для удобства необходимо выразить ребра как: km = d, kl = e и lm = f, используя следующее уравнение через известные параметры треугольника.
- Все стороны: Lm = 2 * (d * e * p * (p — f))^(½) / (d + e), Lк = 2 * (d * f * p * (p — e))^(½) / (d + f) и Ll = 2 * (d * f * p * (p — e))^(½) / (d + f). Параметр «р» — полупериметр, т. е. р = (d + e + f) / 2.
- Стороны и угол: Lm = (2 * d * e * cos (∠M)) / (d + e), Lk = (2 * d * f * cos (∠K)) / (d + f) и Ll = (2 * f * e * cos (∠L)) / (f + e).
Соотношения позволяют найти длины Lk, Lm и Ll, а также другие параметры треугольника. Обратите внимание, что углы во второй группе уравнений соответствуют биссектрисам, вытекающим из них.
Поэтому, чтобы решить задачу о длине биссектрисы, необходимо знать теорию, доказательства теорем, свойства и основные соотношения.
Мы узнали о пересечении отрезков треугольника, выделили и доказали две части теоремы. Мы доказали, что в треугольнике существует только одна зарегистрированная окружность, и узнали о золотом пересечении треугольников.
Свойства биссектрисы
1Биссектриса треугольника делит угол пополам.
2Биссектриса угла треугольника делит противоположную сторону на коэффициент, равный отношению двух смежных сторон ()
3. точки биссектрисы угла треугольника равноудалены от стороны этого угла
4. биссектрисы внутренних углов треугольника пересекаются в точке, которая является центром окружности, вписанной в этот треугольник.
Некоторые формулы, связанные с биссектрисой треугольника
(Доказательство типа можно найти здесь.) Здесь, — длина биссектрисы, проведенной на стороне, и — сторона треугольника относительно вершины соответственно, а — длина отрезка, на который биссектриса делит эту сторону.
Рекомендуем посмотреть видео, в котором показано применение всех вышеперечисленных свойств биссектрисы.
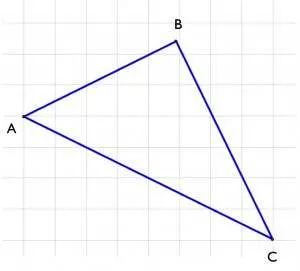
Задача, изучаемая в видео: 1. В треугольнике ABC со сторонами AB = 2 см, BC = 3 см и AC = 3 см проведена биссектриса BM. Найдите длины отрезков AM и MC; 2. Найдите биссектрисы внутреннего угла при вершине A и внешнего угла при вершине C треугольника ABC, пересекающегося в точке M. B равен 40, а угол C равен 80 градусам 3. Найдите радиус окружности, вписанной в треугольник, учитывая, что стороны квадратной клетки равны 1.
Вас также может заинтересовать этот короткий видеоурок, в котором применяется одно из свойств биссектрисы
Согласно Теореме 3, имеем. $ OB = OC, Ј OB =OA$. Следовательно, $ OA =OC$. В этом случае $O$ равноудалена от отрезка $AC$ и, следовательно, находится на центральной вертикали $p$.
Трисектриса. Теорема Морли
Угловые ангиограммы — это два радиуса, которые делят угол на три равные части.
Теорема Морли о триптихе — одна из важнейших геометрических теорем триптиховой геометрии. Он был обнаружен только в 1904 году. Невозможность состричь волосы на углах, очевидно, является одной из причин, по которой это замечательное событие оставалось незамеченным до начала 20-го века.
Пересечение смежных треугольников любого треугольника является вершиной правильного (равнобедренного) треугольника.
Стрижка угла — это проблема деления определенного угла на три равные части путем его построения с помощью компаса и линейки. Другими словами, необходимо построить угловой треугольник.
Наряду с квадратурой круга и удвоением куба, это одна из классических нерешенных задач на построение, известных со времен Древней Греции.
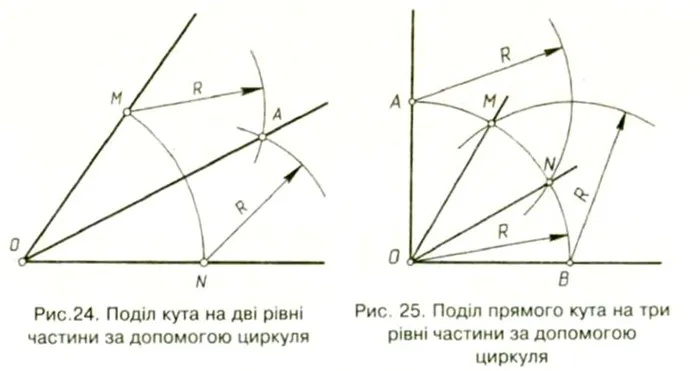
Он делит прямой угол на три равные части.
Эту проблему можно решить с помощью нескольких углов, однако в прессе иногда публикуются некорректные методы стрижки углов с помощью компаса и линейки.








