Вероятность того, что Аня принадлежит к одной из групп, равна 1. Вероятность того, что Нина находится в той же группе, равна 2 из 20 (в группе осталось 2 места и 20 человек). 2/20 = 1/10 = 0,1.
Как решать задачи на вероятность?
Для того чтобы сдать общий государственный экзамен, необходимо знать, как решать задачи на вероятность. Этот предмет уже преподается в 8-м и 9-м классах. Не многие студенты относятся к этому с энтузиазмом. при решении этих задач. Для их решения Они должны быть очень осторожны и умны с формулами.
В этой статье я постараюсь объяснить все как можно проще. решение таких задач по теории вероятностей Я научу вас работать с формулами и объясню особые свойства формул. решения Определенные виды проблем. Давайте сначала попробуем понять, что такое «Что такое вероятность?» простыми словами.
Теория вероятностей как следует из названия, занимается с вероятностями. Нас окружает множество вещей и явлений, о которых наука, какой бы развитой она ни была, не может сделать точных предсказаний.
Мы не знаем, какую карту мы наугад возьмем из колоды или сколько дней в мае будет идти дождь, но, имея некоторую дополнительную информацию, мы можем делать прогнозы и вычислять вероятности эти случайные события.
Таким образом, мы имеем дело с фундаментальным понятием случайного события — явлением, поведение которого невозможно предсказать, опытом, результат которого нельзя просчитать заранее, и т.д. Это вероятности событий, рассчитываемых в типовых задачах.
Строго говоря, вероятность — это функция, принимающая значения от 0 до 1 и характеризующая конкретное случайное событие. 0 — событие практически невозможно, 1 — событие практически определено, 0,5 (или «50/50») — при равных вероятностью произойдет событие или нет.
Вся наша жизнь состоит из случайных событий, которые могут произойти, а могут и не произойти. Например: сегодня вы идете на экзамен, билет для которого вы знаете лучше других, а получите вы его или нет — случайность. Так как билетов всего 20, а вытянуть нужно только один, мы можем определить вероятность, какой из них даст вам желаемый билет. Эта вероятность шанс 1 к 20, так что 1 к 20
или 1/20 или 0,05.
Формула вероятности
Формула для расчета вероятности выглядит следующим образом: где P – вероятность события;
m — количество вариантов, которыми мы удовлетворены (количество благоприятных исходов),
n — общее количество вариантов (возможных исходов).
Логично, что число благоприятных исходов всегда меньше общего числа исходов, то есть мы делим меньшее число на большее. Таким образом, вероятность всегда лежит в диапазоне от 0 до 1.
Как решать задачи с перечислением
Этот тип задачи отличается от предыдущих только тем, что объекты в ней являются номинальными. Расчеты производятся по одной и той же формуле:
Ниже приведен пример такой проблемы.
Задача
В его школьной сумке лежат книги по алгебре, геометрии, химии, биологии и литературе. Вася, не глядя, берет одну из книг. вероятность Откуда он взял учебник по алгебре?
Решение. Несмотря на то, что сейчас эти темы носят номинальный характер, принцип решения проблема остается прежней. Общее число вариантов (т.е. учебников в портфеле) равно 5. Число вариантов, которые нам нужны (т.е. учебник алгебры), равно 1. Следовательно, вероятность события, которые нам нужны, одинаковы:
Независимые события в теории вероятностей
Если вероятность наступление одного события не зависит от наступления другого события и наоборот, то эти события называются независимыми.
Если события независимы, то их вероятности они умножаются. В результате мы… вероятность одновременное наступление этих событий.
Рассмотрим проблему с независимыми событиями.
Задача
Стрелок стреляет шесть раз по мишени. Вероятность попадания в цель при каждом выстреле равна 0,8. Какова вероятность что стрелок попадает в цель все 6 раз подряд? Округлите результат до ближайших сотых долей.
Решение. Задача состоит из 6 независимых событий, т.е. 6 выстрелов. Вероятность для каждого из них равна 0,8. Чтобы найти вероятность одновременное наступление этих независимых событий, необходимо найти вероятности этих событий. Таким образом:
Р = 0,8 * 0,8 *0,8 * 0,8 *0,8 * 0,8 = 0,262144
Округлите результат до ближайшей сотой единицы и получите 0,26.
Итак, вероятность Вероятность того, что стрелок попадет в цель все 6 раз подряд, равна 0,26.
Вероятность того, что Аня принадлежит к одной из групп, равна 1. Вероятность того, что Нина находится в той же группе, равна 2 из 20 (в группе осталось 2 места и 20 человек). 2/20 = 1/10 = 0,1.
Противоположные события
Два события называются противоположными, если они несовместимы в данном тесте и одно из них обязательно произойдет. Вероятности противоположных событий равны 1. Событие, противоположное событию $A$, обозначается $$.
Два события $A$ и $B$ считаются независимыми, если вероятность наступление одного события не зависит от того, наступит или нет другое событие. В противном случае события называются зависимыми.
Вероятность произведения двух независимых событий $A$ и $B$ равна произведению двух событий вероятностей:
Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый лотерейный билет, равна
Несовместные события
Два события $A$ и $B$ называются несовместимыми, если не существует исходов, которые одновременно благоприятствуют и событию $A$, и событию $B$. (События, которые не могут происходить одновременно).
Вероятность суммы двух несовместимых событий $A$ и $B$ равна сумме. вероятностей этих событий:
На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность того, что это вопрос на тему «Квадратные уравнения», равна
Совместные события
Два события называются совместными, если наступление одного из них не исключает наступления другого события в том же процессе. В противном случае события называются несовместимыми.
Вероятность суммы двух общих событий $A$ и $B$ равна сумме вероятностей этих событий минус вероятность их произведения:
В фойе кинотеатра стоят две одинаковые кофемашины. Вероятность того, что в конце дня в автомате закончится кофе, равна $.6$. Вероятность того, что в обеих машинах закончится кофе, равна $32. Найдите вероятность того, что в обеих машинах закончится кофе. вероятность что в конце дня по крайней мере в одной из машин закончится кофе.
По крайней мере, символизировать события:
$A$ = кофе заканчивается в первом автомате,
$B$ = во втором автомате закончился кофе.
$A-B =$ В обеих машинах закончился кофе,
$A + B =$ кофе готов хотя бы на одной машине.
По условию, $P(A) = P(B) = 0,6; P(A-B) = 0,32$.
События $A$ и $B$ являются общими событиями, вероятность сумма двух общих событий равна сумме вероятностей этих событий уменьшилось на на вероятность их произведения:
,3$. Вероятность того, что это вопрос об иррациональном уравнении, равна .18$. Не существует вопросов, относящихся одновременно к этим двум темам. Найти вероятность что студент получит вопрос по любой из этих двух тем.
Эти события называются непоследовательными, потому что студент получает один вопрос LEE по квадратным уравнениям и один вопрос LEE по иррациональным уравнениям. Невозможно охватить обе темы одновременно. Вероятность суммы двух несовместных событий $A$ и $B$ равна. вероятностей этих событий:
,15$. Вероятность выигрыша второго лота составляет .12$. Иван Иванович участвует в обоих розыгрышах. Предполагая, что розыгрыши не зависят друг от друга, вы находите вероятность что Иван Иванович выиграет оба розыгрыша.
Вероятность $P(A)$ состоит в том, что он выиграет первый тираж.
Вероятность $P(B)$ выигрыша во втором тираже.
События $A$ и $B$ являются независимыми событиями. То есть, чтобы найти вероятность что оба события произошли, необходимо найти произведение вероятностей
События $A$ и $B$ являются общими событиями, вероятность сумма двух общих событий равна сумме вероятностей этих событий уменьшилось на на вероятность их произведения:
Как решать задачи с перечислением
Этот тип задачи отличается от предыдущих только тем, что объекты в ней являются номинальными. Расчеты производятся по одной и той же формуле:
Ниже приведен пример такой проблемы.
Задача 4
В его школьной сумке лежат книги по алгебре, геометрии, химии, биологии и литературе. Вася, не глядя, берет одну из книг. вероятность Откуда он взял учебник по алгебре?
Решение. Несмотря на то, что сейчас эти темы носят номинальный характер, принцип решения проблема остается прежней. Общее число вариантов (т.е. учебников в портфеле) равно 5. Число вариантов, которые нам нужны (т.е. учебник алгебры), равно 1. Следовательно, вероятность события, которые нам нужны, одинаковы:
Как решать задачи с фиксированными элементами: разбираем на примере
Задачи на вероятность с фиксированными элементами, сводятся к стандартным задачам на вероятность, но мы должны вычесть 1 из элементов m и n.
Давайте разберемся с этим на примере.
Задача 5
Задача 8. 73 человека участвуют в матче по борьбе. Из Москвы приехали 25 участников, в том числе Б. Егоров. Участники делятся на пары по жребию. Что такое вероятность В результате какой жеребьевки соперником Б. Егорова станет участник из Москвы? Округлите результат до сотых.
Решение. В этой задаче есть один фиксированный элемент — B. Егоров. Этот фиксированный элемент вычитается из элементов m и n.
Таким образом, общее число участников составляет 73. Однако Б. Егоров уже выбран и поэтому не участвует в розыгрыше. Поэтому мы исключаем его из общего числа и получаем n = 72. Нас интересуют только участники из Москвы в возрасте 25 лет. Но опять же, Б. Егоров уже выбран, поэтому он не участвует в жеребьевке. Таким образом, число подходящих выборов для нас равно m = 24. Теперь рассчитаем по нашей формуле: Таким образом, вероятность то, что соперником Б. Егорова будет участник из Москвы, равен 0,33.
Мы еще раз заявляем. Если в задаче есть фиксированный элемент, мы вычитаем единицу из m и n, а затем решаем проблему, используя стандартную формулу для нахождения вероятности.
Как решать задачи с двумя кубиками: используем таблицы
Таблицы полезны при решении Задача, в которой мы имеем дело с двумя кубиками. Например.
Задача 6
Петя бросает две игральные кости. Что такое вероятность что она получит в сумме не менее 9 баллов.
Решение. При такой проблеме лучше всего сделать стол. Горизонтально расположите точки, которые могут выпасть на первом кубике, т.е. числа от 1 до 6. А по вертикали размещаем числа, которые могут выпасть на втором кубике, т.е. тоже числа от 1 до 6. Нарисуем таблицу:
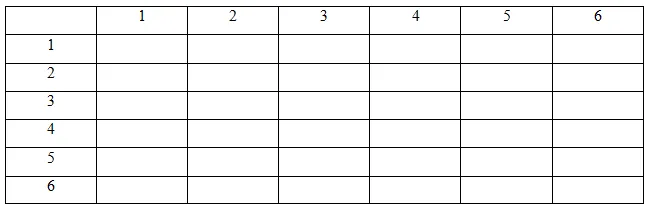
Затем мы заполняем таблицу. Для этого мы записываем сумму чисел в пересечении этой ячейки. Например, заполним первый ряд. В клетке на пересечении двух единиц получается 1 + 1 = 2, затем мы пересекаем 2 и 1 и получаем 2 + 1 = 3, затем 3 + 1 = 4, затем 4 + 1 = 5, затем 5 + 1 = 6, и в последней клетке этого ряда получается 6 + 1 = 7: У нас есть таблица со всеми возможностями для выпавших значений двух игральных костей и их суммы.
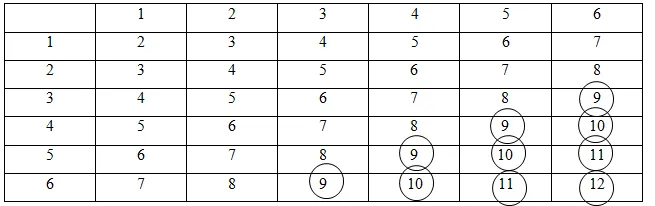
Давайте вернемся к нашей проблеме. Мы должны были найти вероятность что на кубике выпадет сумма не менее девяти очков. Поэтому отметьте в таблице значения, которые больше или равны 9: Таким образом, количество вариантов, которые нам подходят (подсчитайте количество обведенных цифр), равно m = 10.
А общее количество возможных вариаций значений куба: n = 6 * 6 = 36.
Следовательно, вероятность Что выбор, который мы хотим сделать, окажется одинаковым: Итак, вероятность сумма не менее 9 очков на игральной кости равна 0,27.
Задача 7
Маша бросает две игральные кости. Что такое вероятность что игральные кости дают 6 очков? Округлите результат до ближайших сотых долей.
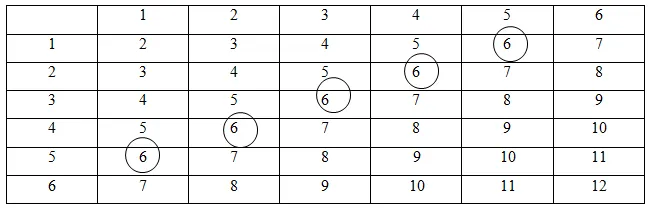
Решение. Возьмем нашу таблицу и найдем значения, когда на кубиках выпадает 6 очков: Таким образом, количество вариантов, которые мы имеем (подсчитайте количество обведенных цифр), равно m = 5.
А общее количество возможных вариаций значений куба: n = 6 * 6 = 36.
Следовательно, вероятность Вероятность выпадения соответствующей вариации такая же: чтобы преобразовать 5/36 в десятичную дробь, нужно разделить 5,00000 на 36, в результате получится 0,13888. Округление до сотых долей дает 0,14.
Итак, вероятность Если кубик показывает сумму 6 очков, то она равна 0,14.
Чтобы добиться успеха в США, вам необходимо знать, как решать задачи на вероятность. Эта тема изучается в школе уже в 8 или 9 классе. Но многие студенты останавливаются при решении этих задач. Для их решения Они должны быть очень осторожны и умны с формулами.
Некогда решать? Найди решенную задачу
Готовые решения Задания для всех классов теории вероятностей, Более 10 000 примеров! Найдите свою проблему:
Пример 2. Какова вероятность Что за 8 подбрасываний монеты гребень выпадает 5 раз?
Снова по схеме решения задач на вероятность Подумайте над этой проблемой:
- В задаче идет речь о серии одинаковых испытаний — бросаний монеты.
- Вводим основное событие $X$ = (При 8 бросаниях монеты герб выпадет 5 раз).
- Так как в задаче происходит несколько испытаний, и вероятность наступление события (гребня) одинаково для каждой попытки, это система Бернулли. Запишем формулу Бернулли, которая описывает следующее. вероятность того, что из $n$ бросков монет герб выпадет ровно $k$ раз: $ P_(k)=C_n^k \cdot p^k \cdot (1-p)^.$
- Записываем данные из условия задачи: $n=8, p=0,5$ (вероятность выпадения герба в каждом броске равна 0,5) и $k=5$
- Подставляем и получаем вероятность$ P(X)=P_(5)=C_8^5 \cdot 0.5^5 \cdot (1-0.5)^=\cdot 0.5^8=\cdot 0.5^8= 0.219.$ Задача решена.
Задача 5: При производстве подшипников диаметром 70 мм вероятность что диаметр отклоняется от заданного менее чем на 0,01 мм, составляет 0,961. Найти вероятность что любой подшипник имеет диаметр менее 69,99 мм или более 70,01 мм.
Теория вероятностей для сдачи ОГЭ и ЕГЭ
Справится с задачей по теории вероятности Это можно сделать довольно легко, если вы знаете формулу, с помощью которой вероятности и если вам посчастливилось столкнуться с этой проблемой. До сих пор практика показывала, что на экзамене задачи легче, чем в детекторе.
Доклады из категории «На тарелке столько пирогов, найдите вероятность, вишневый пирог», с кубиками/монетами, а также задания типа «Найти вероятность что ручка не пишет, когда вероятность того, что он делает, составляет 0,6».
Все остальные типы проблем считаются сложными, потому что не каждый может справиться с ними без определенных знаний.
Начнем анализ задач с формулы для нахождения вероятности:
P=m:n, где P – вероятность любое событие, m — благоприятные события (это то, о чем спрашивается в вопросе), n — все возможные события.
Рассмотрим поиск благоприятных событий на примере.
#1.
Кубик бросается дважды. Сколько элементарных результатов опыта говорят в пользу события A = «сумма очков равна 10»?
Задайте себе вопрос: в каких случаях сумма баллов равна 10?
| 1 кубик | 2 кубика | |
| 1 | 4 | 6 |
| 2 | 5 | 5 |
| 3 | 6 | 4 |
Все это благоприятные события. Всего их 3.
Давайте теперь рассмотрим несколько простых проблем.
Самые простые проблемы вероятности.
#2.
На тарелке лежит 15 пирожков. У четырех из них есть вишни, у пяти — яблоки, а у остальных — абрикосы. Вова берет пирожок наугад. Найти вероятность Что она получит абрикосовый пирог.
Наиболее благоприятными являются пирожные с абрикосами. На тарелке находится 15-4-5=6 фигур.
Все возможные события — это все торты. Их 15.
Вероятность = Благоприятная : Все возможно, т.е.
. Обратите внимание, что, что вероятность не может быть больше 1! Причина этого в том, что 100%. вероятность равна 1.
#3.
На научной конференции выступят 3 докладчика из Германии, 2 из России и 5 из Японии. Найти вероятность что спикер от России будет выступать последним, когда порядок выступлений определяется по жребию.
Наиболее благоприятные события происходят с русскоязычными. Их два.
Все возможные события — это прибытие всех выступающих. Есть 3+2+5=10.
#4.
Из слова «МАТЕМАТИКА» случайным образом выбирается одна буква. Найти вероятность что эта буква оказывается гласной.
Благоприятными фактами являются гласные буквы. Их пять.
Все вероятные факты — это все буквы слова. Их десять.
#5.
Слуга выбирается по жребию из класса, состоящего из 12 мальчиков и 8 девочек. Узнать вероятность что ответственным лицом будет мальчик.
Благоприятные события касаются только мальчиков. Их 12.
Все вероятные события — это все мальчики в классе. Есть 12+8=20.
#6.
Перед началом первого раунда чемпионата по бадминтону участники случайным образом делятся на пары. Всего в соревнованиях участвуют 26 бадминтонистов, в том числе 10 участников из России, включая Руслана Орлова. Узнайте вероятность Сыграет ли Руслан Орлов в первом круге с кем-нибудь из бадминтонистов из России?
Задачи и решения задач на вероятность
Задача 1: Выберите наугад число из натуральных чисел от 23 до 37. Найти вероятность что оно не делится на 5.
Решение:
Вероятность — это отношение числа благоприятных вариантов к общему числу вариантов.
Всего в этом интервале 15 номеров. Из них только 3 делятся на 5, поэтому не делятся на 12.
Значит, вероятность такова:
Задача 2: Два ученика в классе случайным образом выбираются для дежурства в столовой. Какова вероятность того, что два ученика из двух разных школ будут назначены дежурными по столовой? вероятность у двух мальчиков будет смена, если в классе 7 мальчиков и 8 девочек?
Решение: Вероятность — это отношение числа благоприятных вариантов к общему числу вариантов. В классе 7 мальчиков, это благоприятные варианты. А всего в школе 15 студентов.
Вероятность того, что первый человек, поступивший на службу, — мальчик:
Вероятность того, что второй человек на службе — мальчик:
Потому что оба должны быть мальчиками, вероятности перемножим:
Задача 3: В самолете есть 12 мест возле аварийных выходов и 18 мест за перегородками, разделяющими салоны. Остальные сиденья неудобны для высокого пассажира. Пассажир Б — высокий. Найти вероятность что пассажиру B будет предоставлено удобное место при регистрации, если общее количество мест в самолете составляет 300.
Решение: Пассажир B имеет 30 комфортабельных мест (12 + 18 = 30), а всего в самолете 300 мест. Поэтому вероятность что пассажир B получит удобное место, равна 30/300, т.е. 0,1.
Задача 4: В учебнике математики 25 рабочих листов; 10 из них содержат вопрос о неравенствах.
Найдите вероятность Можно предположить, что случайно выбранный бюллетень не будет содержать вопрос о неравенстве.
Решение: 15 из 25 карточек не содержат вопроса о неравенствах, поэтому. вероятность Вероятность того, что на случайно выбранной карточке у ученика не будет задачи на неравенства, равна 15/25, т.е. 0,6.
Задача 5. В коллекции 35 карточек по химии, и 7 из них содержат вопрос о кислотах.
Найдите вероятность Можно предположить, что вопрос о кислотах задается не случайно выбранному кандидату.
Решение: 28 из 35 билетов не содержат вопроса о кислотах, поэтому. вероятность Вероятность того, что студент не ответит на вопрос о кислоте в случайно выбранном билете на экзамене, равна 28/35, т.е. 0,8.
Проблема 6. В среднем 2 из 500 проданных садовых насосов протекают. Найти вероятность что случайно выбранный насос не имеет утечки.
Решение: Если 2 из 500 насосов негерметичны, то 498 негерметичны. Поэтому, вероятность для выбора хорошего насоса составляет 498/500, т.е. 0,996.
Задача 7. Вероятность того, что новый пылесос находится на гарантии, равна 0,065. В одном городе ремонтная мастерская получила по гарантии 70 из 1000 пылесосов, проданных за год.
Насколько частота наступления события «гарантийный ремонт» отличается от частоты наступления события «гарантийный ремонт»? его вероятности в этом городе?
Решение: Частота события «гарантийный ремонт» составляет 70/1000, т.е. 0.07. Она отличается на 70% от прогнозируемой частоты, т.е. 70% от частоты гарантийных ремонтов. вероятности на 0,005 (0,07 — 0,065 = 0,005).
Задача 8. В чемпионате по гимнастике участвуют 50 гимнасток. 18 — из России, 14 — из Украины, остальные — из Беларуси. Порядок, в котором выступают гимнастки, определяется жеребьевкой.
Вероятность нескольких событий
Задание 1. Перед началом волейбольного матча капитаны команд тянут жребий, чтобы определить, какая команда начнет матч. Стартовая команда играет поочередно с командами «Ротор», «Мотор» и «Стратор». Найти вероятность что стартер будет играть только во второй игре.
Решение:
Тип вопроса: комбинация событий.
Нас устраивает следующий вариант: «Статор» не запускает первую игру, запускает вторую игру, не запускает третью игру. Вероятность этой последовательности событий равна произведению вероятностей каждого из этих событий. Вероятность каждого из этих событий равна 0,5, поэтому: 0,5 — 0,5 — 0,5 — 0,5 = 0,125.
Задача 2: Футбольная команда должна набрать не менее 4 очков в двух играх, чтобы пройти в следующий раунд соревнований. Если команда выигрывает, она получает 3 очка, если играет вничью — 1 очко, а если проигрывает — 0 очков. Найти вероятность команда переходит в следующий раунд соревнований. Помните, что в каждой игре вероятности Выигрыш и проигрыш равны и равны 0,4.
Решение:
Тип вопроса: комбинация событий.
Существует несколько вариантов задания:
| Игра №1. | Игра №2. | Вероятность этой вариации |
| 3 | 1 | 0,4 — 0,2 = 0,08 |
| 1 | 3 | 0,2 — 0,4 = 0,08 |
| 3 | 3 | 0,4 — 0,4 = 0,16 |
Вероятность того, что произойдет одна из этих 3 возможностей, равна сумме вероятностей каждой из этих трех вероятностей: 0,08 + 0,08 + 0,08 + 0,08 + 0,16 = 0,32.
Задача 3. Класс состоит из 21 ученика. Есть два друга: Аня и Нина. Класс случайным образом делится на 7 групп по 3 человека. Найти вероятность что Аня и Нина будут в одной группе.
Решение:
Тип вопроса: сократите группы.
Вероятность того, что Аня принадлежит к одной из групп, равна 1. Вероятность того, что Нина находится в той же группе, равна 2 из 20 (в группе осталось 2 места и 20 человек). 2/20 = 1/10 = 0,1.
Задача 4: У Пети в кармане было 4 рублевые монеты и 2 двухрублевые. Петя, не глядя, положил около 3 монет в другой карман. Найти вероятность что обе рублевые монеты находятся в одном кармане.
Решение:
Метод 1
Тип проблемы: Редукционные группы.
Представьте, что шесть монет разделены на две группы по три монеты в каждой. Вероятность того, что первая монета рубль попадет в один из карманов (групп), равна 1.
Вероятность того, что две монеты по две рупии упадут в один и тот же карман, равна числу мест, оставшихся в этом кармане/числу мест, оставшихся в обоих карманах = 2/5 = 0,4.
Метод номер 2
Тип вопроса: комбинация событий.
К этой проблеме подходят по-разному:
Если Петя переложит три из четырех рублевых монет в другой карман (а две рублевые — нет) или если он переложит обе рублевые монеты и одну рублевую монету в другой карман одним из следующих трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1; 2, 2, 1. Вы можете нарисовать это на схеме (Петя перекладывает их в карман 2, поэтому вычислим вероятности в колонке «карман 2»):
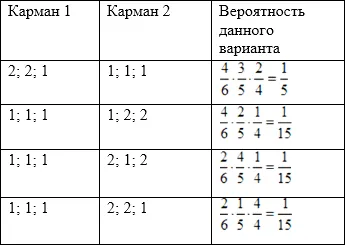
Вероятность того, что возникнет один из этих 4 вариантов, равна сумме вероятностей для каждой из альтернатив:
Дополняющая вероятность
Проблема 1.
Батареи производятся на автоматизированной линии. Вероятность того, что конечный аккумулятор окажется бракованным, составляет 0,02. Перед упаковкой каждый аккумулятор проходит через систему контроля. Вероятность того, что система отбракует дефектный аккумулятор, равна 0,97. Вероятность того, что система случайно отбракует недефектный аккумулятор, равна 0,05.
Найдите вероятность Вероятность того, что случайно выбранный аккумулятор будет забракован.
Решение:
Есть 2 варианта, которые нам подходят:
Вариант A: Батарея забракована, она неисправна,
Вариант B: Батарея отбракована, она исправна.
Вероятность варианта А: 0,02 ∙ 0,97 = 0,0194,
Вероятность варианта B: 0,05 ∙ 0,98 = 0,049,
Нас устраивает либо первый, либо второй вариант: 0,0194 + 0,049 = 0,0684.
Задача 2: Два завода производят одинаковое стекло для автомобильных фар. Первый завод производит 60% стекла, второй — 40%. Первый завод производит 3% бракованного стекла, второй — 5%. Найти вероятность вероятность того, что стекло, случайно купленное в магазине, окажется бракованным.
Решение:
Вероятность того, что стекло, купленное на первом заводе, бракованное: 0,6 — 0,03 = 0,018.
Вероятность того, что стекло, купленное на втором заводе, бракованное: 0,4 — 0,05 = 0,02.
Вероятность того, что случайно купленное стекло окажется бракованным, равна 0,018 + 0,02 = 0,038.
Задача 3. 10 % плит, произведенных на керамическом заводе, являются бракованными. При контроле качества обнаруживается 80 % бракованных пластин. Оставшиеся пластины можно приобрести. Найти вероятность что пластина, случайно выбранная в момент покупки, не является дефектной. Округлите результат в миллиметрах.
Решение:
Предположим, что для начала у нас есть x пластин (поскольку мы всегда работаем с процентами, ничто не мешает нам работать с конкретными ценами).
Тогда 0,1x — это бракованные пластины, а 0,9x — нормальные пластины, которые поступают в цех сразу. Бракованные удаляются на 80%, т.е. 0,08x, оставляя 0,02x, которые также отправляются в магазин. Таким образом, общее количество тарелок на полках магазина составляет 0,9x + 0,02x = 0,92x. Из них 0,9х будет нормальным. В соответствии с формулой вероятность это 0,9x/0,92x ≈ 0,978.
Задание 4. Игорь Игоревич оценил надежность двух интернет-магазинов на основе отзывов покупателей. Вероятность того, что магазин A доставит товар, равна 0,91. Вероятность того, что товар доставит магазин B, равна 0,89. Игорь заказал товары в обоих магазинах одновременно. Предполагая, что интернет-магазины работают независимо друг от друга, вы находите вероятность что ни один из магазинов не доставит товар.
Решение. Вероятность того, что первый магазин не доставит товар, равна 1 — 0,91 = 0,09. Вероятность того, что второй магазин не доставит товар, равна 1 — 0,89 = 0,11. Вероятность того, что эти два события произойдут одновременно, равна произведению вероятностей каждого из них: 0,09 — 0,11 = 0,0099.
Задача 5: При производстве подшипников диаметром 70 мм вероятность что диаметр отклоняется от заданного менее чем на 0,01 мм, составляет 0,961. Найти вероятность что любой подшипник имеет диаметр менее 69,99 мм или более 70,01 мм.
Решение: Нам дана вероятность для случая, когда диаметр находится в диапазоне от 69,99 мм до 70,01 мм и равен 0,961. Мы можем найти вероятность всех других вероятностей, используя принцип дополнительности. вероятности: 1 − 0,961 = 0,039.
Задача 2: Два ученика в классе случайным образом выбираются для дежурства в столовой. Какова вероятность того, что два ученика из двух разных школ будут назначены дежурными по столовой? вероятность у двух мальчиков будет смена, если в классе 7 мальчиков и 8 девочек?
Задачи с использованием элементов комбинаторики
В этих задачах ответ также определяется формулой P(A) = m/n, но подсчитать число n всех возможных событий и число m благоприятных событий сложнее, чем в предыдущих случаях. Для этого используются различные методы подсчета вариаций и вспомогательных чисел, таблицы, диаграммы («дерево возможностей»). Правила сложения и умножения вариаций, а также готовые комбинаторные формулы для количества перестановок, комбинаций и размещений могут облегчить работу.
Правило дополнения: Если объект A может быть выбран k способами, а объект B — l способами (не такими как A), то объект «либо A, либо B» может быть выбран m + l способами.
Правило умножения: Если объект A может быть выбран k способами и после каждого из этих выборов другой объект B (независимый от объекта A) может быть выбран l способами, то пары объектов A и B могут быть выбраны m-l способами.
Правило умножения также называется «правилом AND», а правило сложения — «правилом OR». Не забудьте проверить независимость режимов для «AND» и несовместимость режимов (не так) для «OR».
Следующие проблемы могут быть решать как по комбинаторным, так и по комбинаторным формулам. Я даю несколько способов решения для каждой проблемы, потому что один способ может решить То, что вы делаете быстро, для других занимает много времени, и потому что одни люди понимают один подход, а другие — другой. Но это не значит, что вы должны использовать все методы. Лучше выучить любимое. У вас есть выбор.
В случайном эксперименте симметричная монета подбрасывается пять раз. Найти вероятность что орел выпадет дважды
Эту задачу можно решить по-разному. Рассмотрим тот, который соответствует названию раздела, т.е. мы применяем только комбинаторные формулы.
Решение
В каждом из пяти бросков монеты может произойти один из следующих исходов — орел или решка — для коротких «о» или «п». Таким образом, результатом серии испытаний будет группа из пяти букв, состоящая из двух начальных букв, т.е. содержащая повторения. Например, «ororr» означает, что орел упал два раза подряд, за чем следует решка, снова орёл и снова решка. Поэтому, чтобы подсчитать количество всех возможных исходов, нужно подсчитать количество размещений от n = 2 до k = 5 с повторениями, которое определяется по следующей формуле.
Благоприятные исходы — орел упадет ровно два раза — это «слова» из пяти букв, состоящих из трех «р» и двух «о», которые могут находиться в разных местах, например, «opppo» или «poopp», то есть это перестановки с повторениями. Их количество определяется по следующей формуле
где n = 5 — количество букв, которые необходимо переставить, n o = 2 и n p = 3 — количество повторений «о» и «р» соответственно.
Согласно классической формуле вероятности результат P = __ 10 32 = 0,3125
Ответ: 0,3125
Однако если вы не знаете этих формул, не нужно бояться экзамена по математике в школе. Не только на уровне GCSE и Basic GCSE, но и на уровне GCSE Proficiency, обычно предлагается серия коротких тестов. В таких случаях можно написать и явно проверить результаты. Попробуйте.
В случайном эксперименте подбросьте симметричную монету три раза. Найти вероятность чтобы орел не выпал ни разу.
Решение задач с применением таблиц
Проблема 14 и Проблема 15
Метод II — Поиск вариантов с помощью таблиц. (Нажмите на символ, чтобы увидеть его).
Попробуйте рассмотреть эти примеры не только как решение как объяснение правил сложения и умножения результатов тестирования и принятия окончательного решения о методе решения для проведения тестов. Что лучше — грубая сила или формула?
Вывод: задачи по теории вероятности этого задания можно решать с одной формулой в один шаг, если вам удастся рассчитать количество возможных и благоприятных событий «на пальцах», системы, таблицы. Однако чем сложнее эксперимент («. монету подбрасывают четыре раза .», «. три кости бросают .»), тем сложнее «простой» эксперимент. решение И чем короче, тем «сложнее» — с формулами, правилами. и теорем.
Но если вы все еще совершаете ошибки при решении классических проблем определения. вероятности, может иметь то же происхождение, что и знаменитая шутка про динозавра. Если это так, перейдите по ссылке на анализ логических планов.
Задачи на правила сложения и умножения вероятностей
Примечание: Мы добавили задачи с правилами сложения и умножения. вероятностей Чтобы ознакомиться с этими проблемами, перейдите по этой ссылке.
Рекомендую почитать:
- Лютикас В.С. Школьнику о теории вероятностей. — М. «Просвещение», 1976.
- Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. Пер. с англ. — М. «Наука», 1985.
Ссылки на другие тесты по математике приведены по стрелке.
Нашли ли вы опечатку или ошибку? Пожалуйста, сообщите об этом. Email: mathematichka@yandex.ru Живые уроки доступны для жителей Сергиева Посада.








