Следующим шагом является концентрация данных в таблице (Таблица 1). Всего имеется девять результатов. Обратите внимание на плюс (курьеру открывает друг) — он равен 3, и мы видим, что вероятность звонка для нужного человека составляет 3/9 или 1/3. Если вы хотите проверить вероятность в процентах, умножьте результат на 100%.
Теория вероятности. Часть 2
Также существуют более сложные вопросы вероятности, связанные с использованием математических задач (чем объяснялось в части 1). Необходимо применять дополнительные правила, умножая шансы и различая общие и несовместимые события.
События называются несовместимыми, если одно из них исключает появление других. Это означает, что может произойти только одно конкретное событие.
Например, можно выделить такие события, как бросок игральной кости, выпадение количества очков или ненужное выпадение количества очков. Эти события не являются случайными.
Считается, что факты сосуществуют, если один из них не исключает другой.
Например, при бросании игральных костей можно выделить такие события, как выпадение ненужного количества очков или кратного трем. Если бросить три, то произойдут оба события.
Сумма событий
Сумма или объединение многих событий — это событие, состоящее хотя бы из одного из этих событий.
Сумма двух несовместимых событий равна сумме вероятностей этих событий.
Например, вероятность получения 5 или 6 очков за один бросок игральной кости обусловлена тем, что оба события (игральная кость 5 и игральная кость 6) не связаны друг с другом, и вероятность того или иного события рассчитывается следующим образом
Общая вероятность двух сосуществующих событий равна сумме вероятностей этих событий без учета их сосуществования.
Например, в торговом центре два одинаковых продавца продают кофе. Вероятность того, что в конце дня в автомате закончится кофе, равна 0,3. Вероятность того, что в обеих кофеварках закончится кофе, равна 0,12. Найдите вероятность того, что к концу дня кофе окажется хотя бы в одном автомате (т.е. либо в одном, либо в обоих одновременно).

Вероятность первого события «кофе окажется в первой машине» и вероятность второго события «кофе окажется во второй машине» равна 0,3. События носят общий характер.
Вероятность того, что первые два события произойдут вместе, равна 0,12.
Поэтому есть вероятность, что к концу дня по крайней мере у одного из продавцов закончится кофе.
Произведение вероятностей
Продуктом (или пересечением) многих событий является событие, которое включает в себя общий вид всех этих событий.
Если два независимых события A и B происходят с вероятностями p(a) и p(b) соответственно, то вероятности событий A и B одновременно равны произведению их вероятностей.
Например, нас интересует, чтобы изысканное блюдо упало на кубики два раза подряд. Оба события независимы, и каждое из них имеет отдельную вероятность. Вероятности для обоих случаев рассчитываются с использованием описанных выше типов.
Однако условия включали «u. правильно решит более 9 задач» u. правильно решит более 8 задач». Так, если «У. решает ровно девять задач» символизируется а, то «У. решает более восьми задач правильно» и b, У. Решение: «У. решает более восьми задач правильно» и b, У. Решение: «У. решает более восьми задач правильно».
Основные формулы теории вероятностей
Теоремы сложения и умножения вероятностей
| Применение | Формула |
|---|---|
| Сложение противоположных событий | P(A) + P(A̅) = 1 |
| Сложение несовместных событий | P(A + B) = P(A) + P(B) |
| Сложение совместных событий | P(A + B) = P(A) + P(B) — P(AB) |
| Умножение независимых событий | P(AB) = P(A) × P(B) |
Основные формулы вычисления




Виды событий
Согласно теории вероятности, события бывают невозможными, случайными и истинными.
Невозможное событие
Это уже известный факт, который происходит во время тестирования. Другими словами, вероятность этого равна нулю. Например, какова вероятность того, что при броске костей (один раз) выпадет 7 очков?
Случайное событие
Этот факт может иметь место или не иметь места, но обычно он точно случаен. Например: какова вероятность появления шкалы очков при бросании игральных костей?
Достоверное событие
Это то, что обязательно произойдет во время испытания, т.е. вероятность этого равна 1. Например, когда бросают игральную кость, какова вероятность того, что она упадет, а не останется в воздухе?
Совместные и несовместные события
Несовместимое событие — это когда одно появление исключает появление другого события (в том же тесте). Например, когда бросают кости, выпадают ли «2» и «3»?
Общие события могут происходить в одно и то же время. Например, два спортсмена одновременно плавают, а два студента сдают экзамен.
Рассмотрим события, данные нам. Нам даны два несовместимых события. Таким образом, вопрос относится к «тригонометрии» или «внешним углам». Согласно теореме вероятности, вероятность несовместимых событий равна сумме вероятностей каждого из них. Мы должны найти сумму вероятностей этих событий, т.е.
Событие и виды событий
Факты являются фундаментальным понятием в теории вероятности. Факты бывают достоверными, слабыми и условными.
Достоверность события заключается в том, что в результате проверки оно обязательно произойдет. Например, упадет камень.
Невозможное событие — это событие, которое, как известно, не может произойти в результате испытания. Например, при падении камень будет взлетать вверх.
Случайность — это событие, которое произойдет или не произойдет в результате испытания. Например, из колоды выпадет туз.
События обычно обозначаются заглавными латинскими буквами. Например, A — это событие, когда из колоды выходит туз; D — это факт, что из колоды выходит семерка.
Несовместимые события — это события, в которых появление одного события исключает появление другого (в том же тесте). Самый простой пример несовместимого события — это пара противоположных событий. События, противоречащие конкретному событию, обычно обозначаются тире вверху и той же латинской буквой. Например.
a0 — Монетный закон — это орел, орел.
ā0 — Бросок монеты будет представлять собой письмо.
Полная группа событий — это серия несовместимых событий, включая одно из этих событий, которое обязательно должно произойти в результате одного испытания.
Алгебра событий
Акт добавления событий подразумевает логическое сопряжение или акт умножения событий.
Сложение событий
Сумма двух событий A и B — это факт A + B. Это означает, что либо событие A, либо B, либо оба события происходят одновременно. Если события несовместимы, последний вариант отменяется. Это означает событие a или событие b.
Это правило распространяется и на большие суммы. Факт а.1 + a2 + a3 + a4 + a5 Это, по крайней мере, одно событие1, a2, a3, a4, a5Если факты несовместимы, то произойдет одно событие из этой совокупности.1или факт2или факт3или факт4или факт5.
Факт (при броске кубика не выпадает 5 очков) — выпадает 1, 2, 3, 4 или 6 очков.
Факт б.1, 2 = b1 + b2 (Падает ниже 2 градусов) Факт состоит из 1 или 2 градусов.
Факт б.ч= b2 + b4 + b6 (число шкалы доступно) — это снижение на 2 или 4 или 6 пунктов.
Умножение событий
Произведением двух событий A и B является событие AB, которое состоит из событий, показанных вместе. Другими словами, распространение АВ означает, что при определенных обстоятельствах оба события А и В относятся к большему числу событий. Продукт1 a2 a3 … a10 При определенных условиях оба факта подразумевают1и факт а2и факт а3… и факт а10.
Рассмотрим тест, в котором подбрасываются две монеты и происходят следующие события
a1 — Орел падает в первую валюту, и
ā1 — В первой валюте есть письмо.
a2 — На второй монете корона падает
ā2 — Во второй валюте находится письмо.
ā проявление буквы1 a1 Имеют ли обе монеты (первая и вторая валюта) кроны?
ā2 ā2 На обеих ли монетах (первой и второй) есть буквы?
ā проявление буквы1 ā2 Имеет ли первая валюта корону, а вторая — букву?
ā1 a2 Первая валюта имеет букву, а вторая — корону.
Классическое определение и формула вероятности
Вероятность события a в некотором испытании является причиной.
p(a) = m/n, где n — общее число всех одинаково возможных базовых исходов конкретного теста, а m — число элементарных исходов, благоприятствующих a.
Вероятность достоверного события равна единице.
Вероятность слабого события равна нулю.
Вероятность случайного события — это положительное событие, ограниченное между нулем и единицей.
Поэтому вероятность каждого события удовлетворяет двойному неравенству 0≤p(a)≤1.
Результаты показывают, что вероятность определенной последовательности меньше, чем вероятность события за один раз. Другими словами, вероятность определенной последовательности является произведением вероятностей каждого события. В одном случае, если вероятность равна 1/2, для трех событий: 1/2*1/2*1/2*1/2 = 1/8.
Теоремы сложения и умножения вероятностей, формулы
![]()
В случае произвольных событий A и B общая вероятность этих событий равна сумме маловероятностей общих событий.
В случае независимых событий A и B, вероятность этих событий равна произведению их вероятностей, в данном случае.
Последние два утверждения называются дополнительной теоремой и умножением вероятностей.
Подсчет количества исходов не всегда так прост. В некоторых случаях необходимо использовать комбинированные типы. Наиболее важным из них является подсчет количества событий, удовлетворяющих определенным условиям. Этот тип подсчета может быть упражнением сам по себе.
Сколько существует способов разместить шесть студентов на шести вакансиях? Первый студент занимает один из шести постов. Каждому из них соответствует пять способов занять позицию для второго студента. Для третьего студента есть четыре фришета, для четвертого — три, а для пятого и шестого студентов понятны уникальные позиции. Чтобы узнать количество всех опций, найдите изделие, обозначенное символом 6! Читается как «шесть фабрик».
В общем случае ответ на этот вопрос дает формула для количества N-элементных пересылок в нашем случае.
Рассмотрим другой случай со студентами. Сколькими способами можно разместить двух студентов на шести пустых местах? Первый студент поймет одно из шести положений. Каждому из них соответствует пять способов занять место второго студента. Чтобы найти количество всех вариантов, найдите продукт.
В общем случае ответ на этот вопрос дает формула для количества размещений n элементов для k элементов.
 Примеры решения задач из ЕГЭ по математике на определение вероятности
Примеры решения задач из ЕГЭ по математике на определение вероятности
Вопрос 1. Из сборника, составленного Ященко.
На тарелке 30 пирожков: три — с мясом, 18 — с капустой и девять — с вишней. Саша выбирает пирог наугад. Найдите возможность для вишни.
.
Задача 2. Из сборника, составленного Ященко.
Каждая партия из 1000 лампочек имеет в среднем 20 неисправных лампочек. Найдите возможные дефекты в случайно отобранных лампах из партии.
Решение: количество работающих ламп равно 1000 — 20 = 980. Тогда вероятность того, что случайно полученная лампочка из партии сработает, равна
Вероятность того, что студент В. правильно решит 9 или более задач в тесте по математике, равна 0,67. Вероятность того, что У. правильно решит 8 или более задач, равна 0,73. Найдите вероятность того, что Y. правильно решит ровно девять задач.
Если представить прямую линию и отметить на ней точки 8 и 9, то мы увидим, что условие «В. правильно решает более восьми задач» содержит условие «В. правильно решает более восьми задач», но не содержит его. Оно относится к условию «W правильно решает девять или более задач».
Однако условия включали «u. правильно решит более 9 задач» u. правильно решит более 8 задач». Так, если «У. решает ровно девять задач» символизируется а, то «У. решает более восьми задач правильно» и b, У. Решение: «У. решает более восьми задач правильно» и b, У. Решение: «У. решает более восьми задач правильно».
![]()
.
В тесте по геометрии учащиеся отвечают на вопросы из списка тестовых вопросов. Вероятность того, что это вопрос по тригонометрии, равна 0,2. Вероятность того, что это вопрос о «внешних углах», равна 0,15. Ни один вопрос не относится к этим двум темам одновременно. Найдите вероятность того, что студент получит вопрос по одной из этих двух тем.
Рассмотрим события, данные нам. Нам даны два несовместимых события. Таким образом, вопрос относится к «тригонометрии» или «внешним углам». Согласно теореме вероятности, вероятность несовместимых событий равна сумме вероятностей каждого из них. Мы должны найти сумму вероятностей этих событий, т.е.
![]()
Комната освещается фонарем с тремя лампами. Вероятность того, что лампочка перегорит через год, равна 0,29. Найдите вероятность того, что хотя бы одна лампочка не перегорит в течение года.
Рассмотрим возможные факты. Есть три лампочки, каждая из которых может перегореть или не перегореть независимо от других. Это независимые события.
![]()
Затем определите варианты этих событий. Используем обозначения: — лампочка горит, — лампочка горит. Непосредственно рядом с ним рассчитайте вероятность события. Например, вероятность наступления события с тремя независимыми событиями: — лампа горит, лампа горит и лампа горит: вероятность события «лампа горит» рассчитывается следующим образом. Вероятность того, что событие противоположно тому, что «лампа выключена», т.е.:.
Вероятность того, что студент В. правильно решит 9 или более задач в тесте по математике, равна 0,67. Вероятность того, что У. правильно решит 8 или более задач, равна 0,73. Найдите вероятность того, что Y. правильно решит ровно девять задач.
Почему интуитивное знание всегда противоречит статистике
Моя бабушка считает, что в Албании людей убивают на каждом шагу. Она не была в стране и не слышала новостей, но ей кажется, что она интуитивно это понимает. Я уверен, что вы много раз испытывали подобное чувство, и я уверен, что вы тоже испытаете. Это называется интуитивным знанием — внутренняя уверенность в том, что наша оценка вернее, чем официальные источники и статистика.
127 убийств на 100 000 человек в целом
Классическое исследование интуитивного знания было проведено Дэниелом Канеманом и Амосом Тверски. Они дали группе студентов задание: оценить высказывания в диапазоне от больше (1 балл) до меньше (8 баллов) по таблице, составленной на основе портретов (Таблица 3).
Портреты выглядели следующим образом. Линда, возраст — старше 30 лет. Умный, он говорит то, что думает. Он изучал философию в университете.
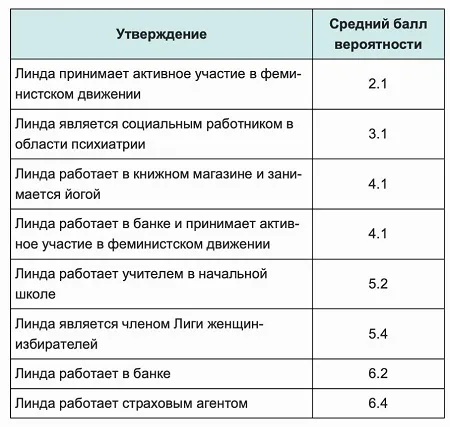
Таблица 3.
Судя по портрету, можно предположить, что Линда участвует в феминистском движении. Однако студент принимал свои решения интуитивно, что привело его к ошибке. Шансы Линды работать в банке и присоединиться к феминистскому движению выше, чем ее шансы работать в банке.
См. таблицу: вероятность того, что вы работаете в банке и присоединились к феминистскому движению, составляет 4,1 балла. Однако первый (работа в банке) и второй (феминистское движение) дают в сумме 8,3 балла. По мнению Тервера, вероятность обоих событий может быть больше, чем вероятность каждого из них. Основное высказывание (4,1 балла) содержит два события и является единым событием. Интуитивное решение будет заключаться в нарушении правила газонокосилки. Это доказано — наши убеждения часто оказываются ошибочными.
С тех пор было проведено несколько экспериментов, подтверждающих предположение Канемана.








