В конце XVI века голландский математик Андриан ван Лемменс, возможно, наиболее известный тем, что вычислил числа PI с 18 правильными знаками, решил бросить вызов всем математикам мира.
Основные понятия
Квадратное уравнение имеет вид ax 2 + bx + c = 0. где a — первый ненулевой коэффициент, b — второй коэффициент и c — свободный член.
Существует три типа квадратных уравнений.
Чтобы определить количество корней в уравнении, следует обратить внимание на невязку сил. Этот тип вывода записывается следующим образом: d = b 2-4ac. его свойства: d = b 2-4ac.
Если второй коэффициент является шкалой, то тип может быть использован для нахождения ненавязчивой мощности.
В математике теорема — это утверждение, доказательство которого было высказано ранее.
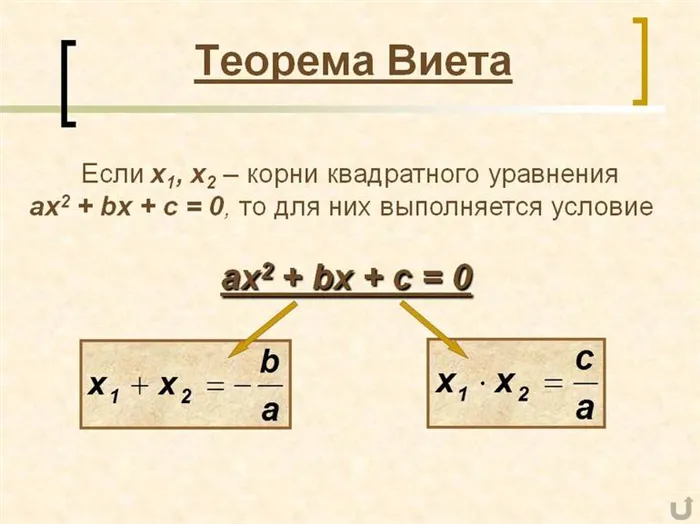
Формула Виета
В школьной геометрии чаще используется теорема Пифагора, в то время как тип Бето играет ведущую роль в школьной алгебре. Теорема заключается в следующем.
Рассмотрим квадратное уравнение, первый коэффициент которого равен 1. Такие уравнения называются редуцированными уравнениями. Сумма корней равна противоположному знаку и второму множителю, а произведение корней равно свободному условию.
Если x 2 + bx + c = 0, то применимы два уравнения, если x₁ и x₂ — корни.
Обычно знаки системы, указанные в скобках, означают, что значения x₁ и x₂ удовлетворяют обоим равенствам.
На следующем примере рассмотрим теорему Вита: x 2 + 4x + 3 = 0.
Корни, которые имеет это уравнение, пока неизвестны. Однако, согласно теореме, сумма этих корней может быть записана как равная с противоположным знаком и вторым коэффициентом. Поскольку оно равно четырем, используется минус четыре.
Произведение корней по теореме соответствует свободному члену. В данном случае свободный термин является третьим. Поэтому.
Нам нужно проверить, равна ли сумма корней -4, а произведение — 3. Для этого найдите корни уравнения x 2 + 4x + 3 = 0.
Вы увидите, что корнями уравнения являются числа -1 и -3. Решение верно, так как их сумма равна второму коэффициенту с противоположным знаком.
Корни -1 и -3 из теоремы должны равняться свободному члену, то есть числу 3. Это условие также выполняется.
В результате проведенных расчетов уравнение подтвердилось.
Он помогает учащимся участвовать в математических курсах, знакомиться с новыми проблемами и повышать успеваемость в школе.
Доказательство теоремы Виета
Если квадратное уравнение x 2 + bx + c = 0, то если его дискретность больше нуля, то существуют два корня, сумма которых равна знаку, противоположному второму коэффициенту, а произведение корней равно свободному члену.
Докажите, что следующие уравнения применимы
Чтобы найти сумму корней x₁ и x₂, замените их соответствующими корнями из правой части типа корня. Вспомните, что в этом квадратном уравнении x 2 + bx + c = 0 наибольший коэффициент равен 1. Таким образом, после замены знаменатель равен 2.
-
Объединим числитель и знаменатель в правой части.
x₁ +x₂= -b.
Далее мы следуем той же процедуре, чтобы доказать, что x₁ *x₂ равно свободному члену c.
-
Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:
x₁ *x₂= c.
Так, сумма корней квадратного уравнения, заданного x 2 + bx + c = 0, равна противоположному знаку (x₁ +x₂= -b) и второму коэффициенту, а произведение корней — свободному члену (x₁ *x₂ = c). Теорема доказана.
Два вышеприведенных уравнения затем используются для записи суммы квадратов. (m1)^ 2 + (m2)^ 2 = (m1)^ 2 + (m2)^ 2 —2 * m1 * m2 —2 * m1 * m2 = (m1 + m2)^ 2-2 * m1 * m2 = 7 2-2 * 12 =25. задача решена: 7, 12, 25.
Общие сведения
Чтобы применить формулу теоремы Вьетнама к квадратному уравнению, необходимо проанализировать некоторые термины и математические определения. Квадратное уравнение вида Am 2 + Bm + C = 0 — это квадратичный многочлен, состоящий из коэффициента A неизвестного квадрата и суммы произведений второго коэффициента, неизвестного количества и постоянной C. Этот многочлен является уравнением только в том случае, если он равен нулю. Постоянная C также называется свободным членом.

Корень — это неизвестное значение, при подстановке которого тождество становится верным. Обратите внимание, что некоторые математические преобразования могут привести к появлению дополнительных радикалов. Это особенно верно для различных подстановок тригонометрических функций. Однако при замене корней равенство не сохраняется. Математики называют их ложными корнями. После решения уравнения эксперты рекомендуют заменить эти значения на исходное уравнение. Эта техника помогает избавиться от нежелательных решений.
Нахождение корней с помощью теоремы Вита является одним из самых быстрых методов, поскольку избавляет людей от ненужных вычислений с помощью уравнений, использующих дискретность.
Виды квадратных уравнений
Квадратичные уравнения существуют в различных видах, поскольку ненулевые коэффициенты встречаются не во всех случаях. Математики классифицировали их на два типа:.

Первое — это уравнение со всеми коэффициентами, кроме нуля (A, B и C). Если число перед неизвестным числом не указано, оно считается равным единице; уравнение без B или C считается неполным. Однако если два последних коэффициента равны нулю, тождество имеет вид: Am2 =0. Кроме того, существует еще один критерий распределения видов, основанный на степени редукции. В соответствии с этим критерием уравнения делятся на редуцированные и нередуцированные.
Первое уравнение должно включать уравнения с коэффициентом 1. Во всех остальных случаях (A> 1) тождество не уменьшается.
Условие использования закона
Правило Вита применимо не ко всем уравнениям. Математики сформулировали важные условия, при которых это правило может быть использовано. Уравнение должно быть сократимым, а дискриминант должен быть больше нуля. Если это условие не позволяет преобразовать уравнение в редукцию, необходимо использовать другие методы квадратур. Вместо этого используются правила Viets.
Существует простой алгоритм преобразования уравнений в требуемую форму. Это простое действие — разделить каждый коэффициент на A. Например, уравнение 4p 2 + 8p + 16 = 0 нужно преобразовать в сокращенное уравнение. Следуя описанному алгоритму, получается следующее уравнение: (4p 2) / 4 + 8p / 4 + 16/4 = 4p 2 + 2p + 4 = 0.
Применение теоремы
Вьетнамская формулировка квадратного уравнения Am2 + Bm + C = 0 выглядит следующим образом Сумма корней соответствует квантору A, полученному с противоположным знаком, а произведение — свободному члену C. Решение получается путем корректировки соответствующих чисел. Однако все теоремы должны быть доказаны.
Чтобы выполнить это действие, необходимо использовать специальный тип для корней, используя ненавязчивые возможности. Для этого необходимо принять два уравнения: m1 + m2 = -b и m1 * m2 = c. Выражение значений корней через обобщенную форму разности позволяет получить такое тождество.
Затем мы должны найти сумму m1 и m2: -b -d^(½)/(2 * a) + -b + d^(½)/(2 * a). Чтобы упростить полученное выражение, используйте этот алгоритм.

- Привести дроби к общему знаменателю: (-B — D^(½)) + (-B + D^(½))/(2 * А).
- Упростить выражение (разложение на множители): -B — D^(½) — B + D^(½)/(2 * А) = (-2B) / (2 * A) = — B / A = -B / 1 (А = 1).
Затем нам нужно доказать, что корневое произведение эквивалентно c. Для этого перемножьте m1 = -b — d^(½) / (2 * a) и m2 = -b + d^(½) / (2 * a). Процесс:.
- Перемножить числители и знаменатели: -B — D^(½) / (2 * A) * -B + D^(½) / (2 * A) = (-B + D^(½)) * (-B — D^(½)) / (4 * A 2 ).
- Упростить: B 2 — D / 4A 2 = B 2 — (-B 2 — 4 * A * C) / 4A 2 = (B 2 — B 2 + 4 * C) / 4 = C (при А = 1).
Второй тип доказывает. Однако перед решением обязательно вычислите значение дискриминанта, так как уравнение имеет только один корень, если d = 0. Формулировка такая: корни AM 2 + BM + C = 0, если сумма M1 и M2 соответствует значению B с противоположными знаками и они соответствуют свободным членам многочлена степени 2. Это заявление имеет квитанцию, которая требует выполнения следующей процедуры.

- Подставить m1 и m2 в исходное уравнение: m 2 — (m1 + m2) * m + m1 * m2 = 0.
- Раскрыть скобки и привести подобные слагаемые: m 2 — (m1 * m — m2 * m + m1 * m2 = (m — m1) * (m — m2) = 0.
- Найти корни тождества в пункте 2: m = m1 и m = m2.
Таким образом, числовые значения M1 и M2 являются корнями уравнения, поэтому теорема доказана. Далее следует рассмотреть заданное кубическое уравнение и способ применения утверждения Виетта.
Кубические равенства с неизвестным
Теорема Виетта также может быть применена к кубическим уравнениям вида a * m 3 + b * m 2 + c * m + d = 0. Коэффициент A должен быть равен 1. Корни можно обнаружить с помощью грубого насилия, но сделать это сложно, поскольку необходимо решить систему из трех уравнений.

Числа M1, M2 и M3 являются корнями. Кроме того, поскольку уравнения являются кубическими, необходимо обратить внимание на формирование ошибочных результатов. Ученые пришли к выводу, что чем выше степень, тем больше ложных ответов. Для поиска решений рекомендуется использовать специальное программное обеспечение. Если у вас нет буфера обмена, вы можете нарисовать график функции, а затем найти расстояния и точки пересечения. Также доступны специальные онлайн-услуги. Такие калькуляторы называются онлайн-калькуляторами.
Квадратные уравнения с коэффициентами x 2, равными 1, называются сокращенными уравнениями. Например, сокращенное уравнение — это уравнение (x^2-11x+30 = 0, квадрат x^2-6x = 0, квадрат x^2-8 = 0)
Доказательство теоремы Виета
Для доказательства теоремы можно использовать известные виды корней, которые образуют сумму и произведение корней квадратного уравнения. Только после этого можно проверить, что они равны.
Предположим, у нас есть уравнение:. Это уравнение имеет следующие корни. Давайте докажем это.
По типам корней квадратного уравнения:.
1. найдите сумму корней:.
Давайте проанализируем это уравнение, поскольку оно у нас именно такое.
Шаг 1. Приведите дроби к общему знаменателю.
Шаг 2. Есть дробь, которая должна открыть кронштейн.
=. Получите дроби, уменьшенные на 2.
Доказал коэффициент суммы корней квадратного уравнения с помощью теоремы Виета.
2. найдите произведение корней.
Докажите это уравнение:.
Шаг 1. Существует правило для умножения дробей, умножающих это уравнение.
Шаг 2. Следующий шаг — умножение скобок на скобки (числитель). Можно использовать тип разности — тип уменьшенного умножения (RMS). Отсюда результаты следующие.
Теперь вспомните определения квадратного корня и измеряемой величины.
Шаг 3. Вспомните решение квадратного уравнения. Таким образом, заменив в последней части вместо D (разрешение), получаем
Шаг 4. Раскройте скобки и вычтите ту же сумму.
Шаг 5. Уменьшите «4a».
Здесь мы доказали аналогию между произведением корней и теоремой Вьетнама.
Важно: Если разрешение равно нулю, то квадратное уравнение имеет только один корень.
Примеры с решениями по теореме Виета
Не находя корней уравнения, найдите сумму, произведение и сумму квадратов корней квадратного уравнения.
Шаг 1. Помните о типе свободы действий. Замените буквы цифрами. Другими словами, заменяется на ,. Поэтому:.
. Если дискриминант больше нуля, то уравнение имеет корень. Согласно вьетнамской теореме, их сумма равна, а произведение равно .
Сумма квадратов корней выражается как их сумма и произведение.
Решите уравнение. Не применяйте квадратное уравнение.
Уравнение имеет корни больше нуля, в зависимости от разрешения (D). Поэтому, согласно теореме Виета, сумма корней этого уравнения равна 4, а произведение — 5. Сначала определите делители, сумма которых равна 4. Это числа 5 и -1. Их произведение равно -5, а сумма равна 4. Поэтому, согласно обратной теореме Виета, они являются корнями уравнения.
Если возможно, найдите сумму и произведение корней уравнения.
. Поскольку дискриминант меньше нуля, уравнение не имеет корней.
Составьте уравнение, в котором каждый корень в два раза больше соответствующего корня уравнения.
Согласно теореме Виета, сумма корней этого уравнения равна 12, а произведение — 7. Это означает, что оба корня положительны.
Сумма корней нового уравнения равна
Согласно обратной теореме вьетнамской теоремы, новое уравнение имеет вид
Получаем уравнение с вдвое большим количеством корней.
Затем мы рассмотрели, как решить уравнение с помощью теоремы Виета. Теорема очень полезна при решении задач, связанных со знаком корней квадратного уравнения. То есть, если свободный член в уравнении является положительным числом и квадратное уравнение имеет действительные корни, то оба они могут быть как отрицательными, так и положительными.
А если свободный член является отрицательным числом и квадратное уравнение имеет действительный корень, то оба они имеют разные знаки. Другими словами, если один корень положительный, то другой корень может быть только отрицательным.
Полезные источники:.
- Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. Алгебра 8 класс: Москва “Просвещение”, 2016 – 318 с.
- Рубин А. Г., Чулков П. В. – учебник Алгебра 8 класс:Москва “Баласс”, 2015 – 237 с.
- Никольский С. М., Потопав М. К., Решетников Н. Н., Шевкин А. В. – Алгебра 8 класс: Москва “Просвещение”, 2014 – 300
Теорема Виса, обратная формула Виса, примеры решения для чайников Обновлено 16 Апр 2020 от Scientific Articles.Ru
Он используется как студентами, так и взрослыми для решения специализированных математических задач. В этой статье вы узнаете больше о том, что представляет собой эта теорема и как использовать ее на практике.
Теорема Виета

Повторяя тему уравнений и неравенств, в этом уроке рассматриваются квадратные уравнения. Вспоминаются такие понятия, как сокращенные квадратные уравнения, формулы для вычисления корней сокращенных квадратных уравнений, теорема Виета и обратная теорема. Также обсуждается применение теоремы Виетта к задачам различной сложности.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим обучающим видео в комплекте, вы должны приобрести его в каталоге и добавить в свой личный кабинет.



Конспект урока «Теорема Виета»
-Повторите такие понятия, как «уравнения с приведенными квадратами».
-Повторите уравнения для вычисления корней квадратных уравнений, теорему Виета и обратную теорему.
— Мы рассмотрим применение теоремы Бето к задачам разного уровня сложности.
Мы говорили, что квадратное уравнение имеет вид: a = 1, b = 1, c = 1, d = 1, e = 1.
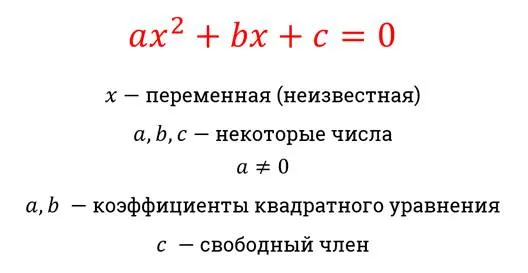
Однако, когда коэффициент a = 1, такие квадратные уравнения имеют специальное название — сокращенные уравнения.
В принципе, все квадратные уравнения могут быть сокращены.
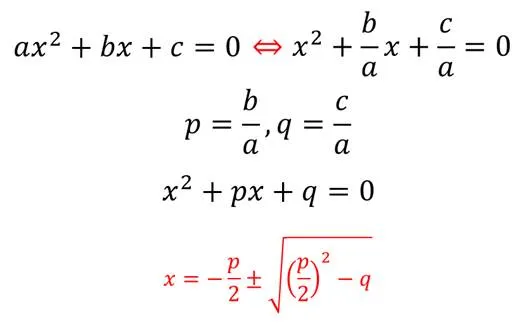
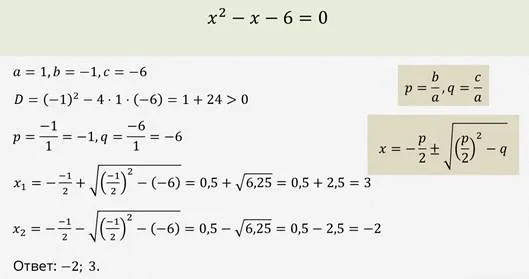
Теорема Виета часто используется для нахождения корней сокращенных уравнений. Однако следует помнить, что сначала необходимо убедиться, что уравнение укоренилось. Для этого необходимо определить признаки идентификации, поэтому вам не нужно искать саму идентификацию.
Запомните эту теорему.
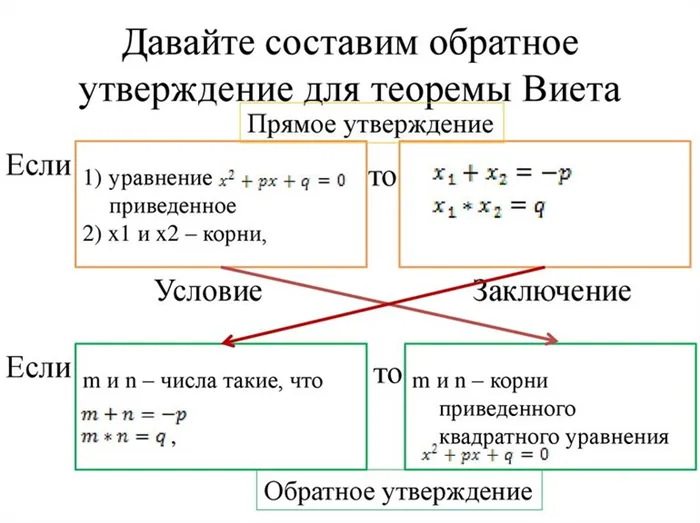
Помните также об обратной теореме.

Эту теорему легко использовать для решения квадратных уравнений. Достаточно найти количество интегралов, произведения которых равны свободным условиям уравнения, а сумма равна второму коэффициенту с обратным знаком.
Важно помнить, что теорема Виетта применима только к данному квадратному уравнению.
Давайте рассмотрим применение теоремы Виетта на конкретном примере.



Для квадратных уравнений общего вида теорема Виетта может быть записана следующим образом
теорема виета для квадратных уравнений общего вида:.

Однако, в принципе, с помощью теоремы Виета можно решать уравнения, в которых коэффициенты остаются неизменными при делении на коэффициент a.
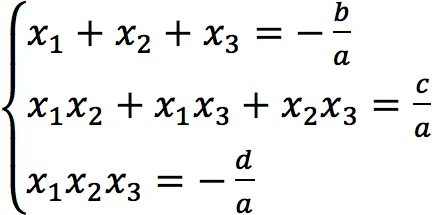
Рассмотрим еще одну подобную проблему.

Давайте рассмотрим один из таких примеров.


Сегодня мы повторили такие понятия, как приведенное квадратное уравнение, которое является разновидностью приведенного квадратного уравнения для вычисления корней приведенного квадратного уравнения. Мы вспомнили обратную теорему, теорему Виетта, и рассмотрели применение теоремы Виетта для решения задач разной степени сложности.








