Свойства правильного многоугольника. Как найти углы многоугольника

Содержание

Положительные многоугольники, которые мы видим весь день, такие как квадраты, треугольники или шестиугольники, формы, из которых сделаны все соты пчел. Чтобы задать положительный многоугольник по отдельности, необходимо знать его углы.

Как найти внешний угол многоугольника

Внутренний угол многоугольника — это угол, образованный двумя соседними сторонами многоугольника. Например, ABC — это внутренний угол.

Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и противоположным продолжением. Например, ∠LBC — это внешний угол.

Количество углов в многоугольнике всегда равно количеству сторон. Это относится к внутренним и внешним углам. Можно построить два равных внешних угла на вершину многоугольника, но всегда рассматривается только один из них. Поэтому, чтобы найти количество углов многоугольника, необходимо измерить количество ребер.

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению 180° и числа ребер без двух.

Где s — сумма углов, 2 d — два прямых угла (т.е. 2 — 90 = 180°), а n — количество ребер.

Проведение всех возможных диагоналей многоугольника ABCDEF из вершины A делит его на треугольники.

Поэтому сумма углов многоугольника равна сумме углов всех получившихся треугольников. Поскольку сумма углов каждого треугольника равна 180° (2 d), то сумма углов всех треугольников равна произведению 2 d их количества.

Этот тип показывает, что сумма внутренних углов постоянна и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна 360° (или 4 d).

Где s — сумма внешних углов; 4 d — четыре правильных угла (т.е. 4 — 90 = 360°).

Сумма внешнего и внутреннего углов каждой вершины многоугольника равна 180° (2 d), так как они являются смежными углами. Например, ¶1 и ∠2:.

Таким образом, если многоугольник имеет n сторон (и n вершин), то сумма внешнего и внутреннего углов всех n вершин равна 2 dn. Чтобы из суммы 2 dn получить только сумму внешних углов, отнимите от нее сумму внутренних углов, т.е. 2 d(n -2).

Что такое внешние углы многоугольника? Сколько внешних углов имеет многоугольник? Какова сумма внешних углов многоугольника?

Внешние углы многоугольника — это углы, примыкающие к внутренним углам.

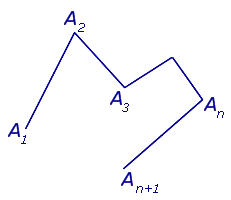
Это связано с тем, что они прилегают к внутренним углам A2A1AN.

Угол 2 также охватывает угол A2A1AN.

Следовательно, ¶2 — это внешний угол верхней части A1.

Таким образом, каждая вершина многоугольника имеет два внешних угла, которые равны друг другу.

Это означает, что N вершин N-образной грани имеют в общей сложности 2N внешних углов.

Поскольку оба внешних угла при вершине равны, мы говорим о сумме внешних углов N-уровней, поэтому рассмотрим внешние углы, взятые при каждой вершине.

(О сумме внешних углов выпуклого многоугольника)

Сумма внешних углов выпуклых многоугольников, взятых из каждой вершины, равна 360º.

Датум.

1, угол 2, угол 3, … где угол n — внешний угол вершины

Аналогично, сумма внешнего и внутреннего углов при вершине каждого из n-угольников равна 180º.

Поэтому сумма всех внутренних углов многоугольника и всех внешних углов многоугольника (взятых из каждой вершины) равна 180º∙n.

Таким образом, сумма всех внешних углов

необходимо было доказать.

Смежные стороны (с общими вершинами) не должны лежать на одной прямой, а несмежные стороны не должны иметь общих точек (т.е. они не должны пересекаться).

Свойства правильного многоугольника

В этой публикации мы рассмотрим основные свойства нормальных многоугольников (включая их сумму), количество диагоналей и центры периферических и внутриклеточных циклов. В нем также рассматриваются виды базового определения размеров (площадь и периметр фигуры, лучи окружности).

Примечание: Определение нормальных многоугольников, их свойства, основы и типы рассматриваются в отдельных публикациях.

Свойство 4

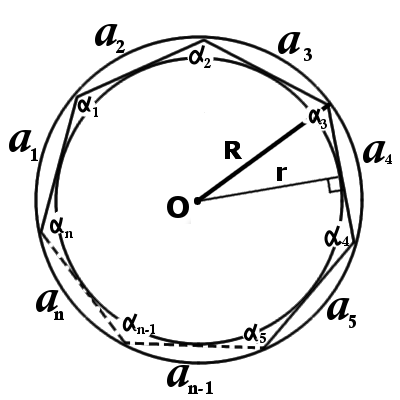
Окружности и периметры могут быть зарегистрированы с помощью обычных многоугольников, центр которых совпадает с центром самого многоугольника.

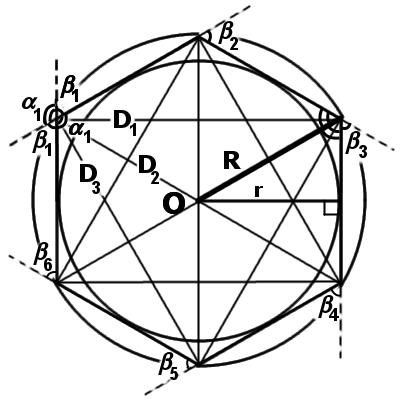
В качестве примера на следующей диаграмме показан обычный шестиугольник (гексагон) с центром O.

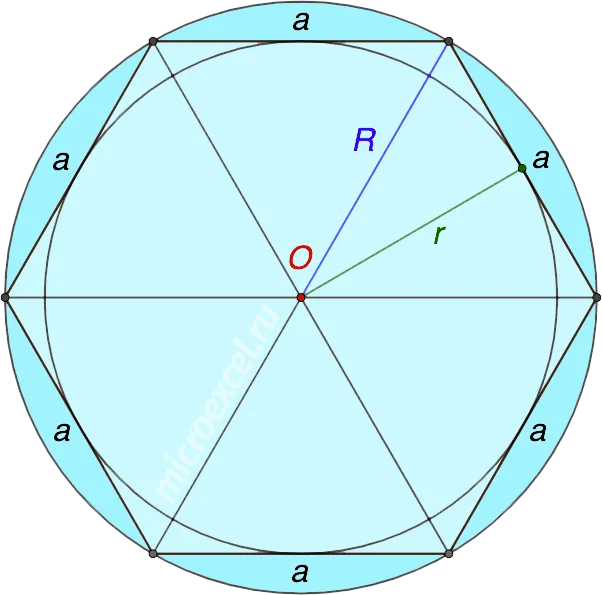
Площадь круга, образованного окружностью, вычисляется по длине (a) на диаграмме в эквиваленте.

Существует взаимосвязь между лучами конечного цикла (R) и площадью (R).

Свойство 5

Зная длину стороны (a) нормального многоугольника, можно вычислить следующие относительные размеры

1. регион:.

2. периметр (P):.

3. радиус области (R):.

4. радиус в ячейке (R):.

Например, многоугольники со стороной ዄ (⌘ displaystyle 4 \) называются четырехугольниками, многоугольники со стороной ዄ (⌘ displaystyle 6 \) называются шестиугольниками и так далее.

Произвольные многоугольники

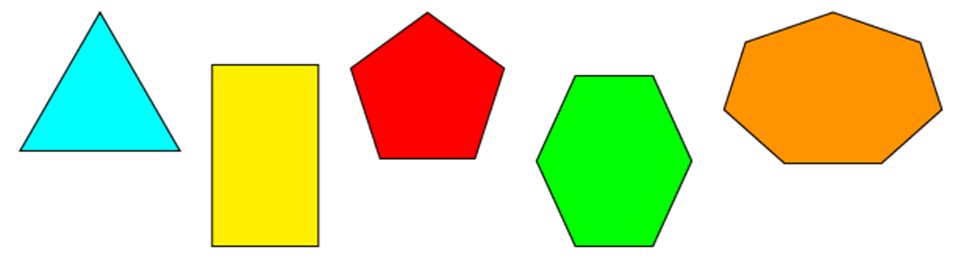
Спланируйте, какие многоугольники у вас есть.

Теперь вопрос: какой из этих полигонов вырвется из ряда?

Внимательно посмотрите на второй многоугольник — он отличается от всех остальных. Что отличает его от других?

Он не является выпуклым многоугольником. Конечно, это математическое название, но оно не противоречит человеческой интуиции.

Здесь мы рассматриваем только выпуклые многоугольники, т.е. 1), 3), 4) и т.д.

Для любого данного многоугольника сумма внутренних углов равна ⌘(⌘ displaystyle 180^o(n-2)⌘), где буква «⌘(⌘ displaystyle n \)» означает количество углов в многоугольнике.

Четырехугольник

Пятиугольник

Шестиугольник

Ах да, я забыл про треугольник.

Треугольник

Сумма углов многоугольника. Доказательство.

Далее разберемся, откуда в конечном итоге взялся тип \(⌘ displaystyle 180^\ окружности (n-2)⌘) многоугольника.

Как вы знаете, трюк, который мы собираемся применить, часто помогает решить различные проблемы.

Теорема о сумме углов многоугольников применима ко всем многоугольникам, но доказательство хорошо и просто только для криволинейных многоугольников.

Теперь разделим многоугольник на треугольники.

Как таковые: спроектировать все диагонали, которые мы можем, из одной точки времени. Сколько их; давайте посчитаем:.

Общий верх: ዄ (ዅ displaystyle n \)

Из вершины ᢙ (⌘ displaystyle b \) мы можем провести диагонали на все вершины, кроме следующей: ᢙ (ᢙ displaystyle b \).

Таким образом, общая диагональ равна \(\ displaystyle (n-3)\). А на сколько треугольников делится наш многоугольник?

Представьте: ⌘ (⌘ displaystyle n-2 ⌘). Рисуем, считаем — есть еще один треугольник.

Таким образом, существует треугольник с \(\ displaystyle n-2 \). Сумма углов многоугольников просто равна сумме углов треугольников, разделяющих многоугольники.

Чему равна сумма углов треугольников? Ты помнишь. Конечно, ⌘ (⌘ displaystyle 180).<>^\ circ \).

Поэтому сумма углов ǫ(ǫ displaystyle n-2 \)треугольников, соответственно, ǫ(ǫ displaystyle 180<>^\ circ \)\), поэтому:.

Сумма углов многоугольника равна \(\ displaystyle 180)<>^\\\\\ circ \)\(\ displaystyle (n-2)\)\)\

Что из этого может помочь? Две вещи:.

Открыть ответы…

Мы постоянно совершенствуем это руководство, и вы можете помочь нам в этом. Неограниченный доступ и использование пособия Yuklava (более 100 статей по всем темам ЕГЭ и ОГЭ, более 2000 решенных задач, более 20 онлайн-учебников)

Правильные многоугольники

Если все углы и все стороны многоугольника равны, то многоугольник называется нормальным.

Пример: квадрат является нормальным четырехугольником, а прямоугольник — нет, даже если все углы равны, а ромб — нет, даже если все стороны равны. Все углы и все стороны должны быть равны.

Первый вопрос.

Можно ли найти значение одного (а значит, и всех) углов нормального многоугольника?

Давайте рассмотрим пример.

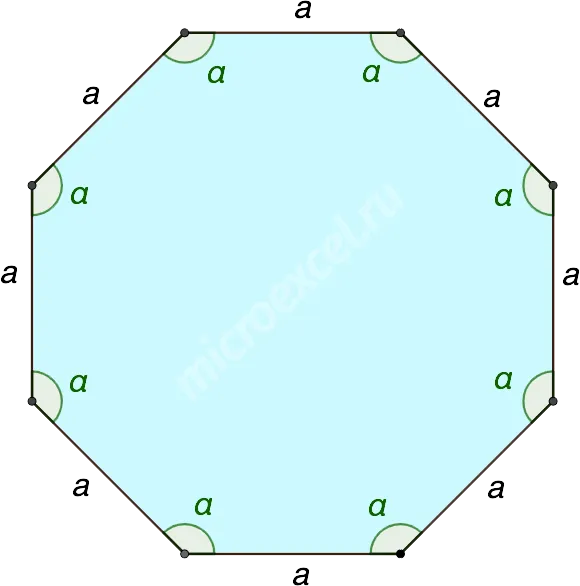
Предположим, например, что у вас есть обычный восьмиугольник.

Сумма всех его углов равна ⌘ (⌘ displaystyle 180)<>^ \ круг \ слева (8-2 \ справа) = 1080<>^\ circ \).

А сколько всего углов? Восемь, конечно. Они все одинаковые.

Поэтому можно найти любой угол. Например, 팀 (팀 displaystyle \ угол A \):.

\ displaystyle \ угол A = \ frac ^ \ circ> = 135<>^\ circ \).

Нормальные многоугольники могут быть вписаны в окружности, а нормальные многоугольники могут быть заключены в окружности.

Центры этих окружностей совпадают.

Кроме того, всегда можно рассчитать отношение радиуса отпечатанного круга к окружности круга.

Снова пример с восьмиугольником.

\（\ displaystyle \ Delta OKG \) \（\ displaystyle OK = r, OG =R).

Это означает, что 팀 (⌘ displaystyle \ frac = \ sin \ angle x \) — и это не просто восьмиугольники!

Чему в этом случае равен ߡ(ߡ displaystyle \ угол x \)?

\Всего половина \(⌘ displaystyle \ угол G \), представьте себе!

Таким образом, ߋ (ߋ displaystyle \ угол x = \ frac ^ \ circ> = 67,5<>^\ circ \).

Нелепо, но да! Поэтому в случае восьмиугольной формы ⌘ (⌘ displaystyle \ frac = \ sin 67.5<>^\ circ \).

Может возникнуть и другой вопрос. Можете ли вы вычислить угол вокруг точки ⌘ (⌘ displaystyle O \)?

И тот же ответ: конечно, можно!

Подумайте еще раз о восьмиугольнике. Здесь вы хотите найти ɑ (ɑ displaystyle ɑ angle ɑ alpha ɑ) (т.е. ɑ displaystyle ɑ angle HOG \).

Открыть ответы…

Таким образом, вы можете найти все о восьмиугольниках, а также об обычных многоугольниках.

Sima 1 июля 2020 года Черт, это действительно круто. И самое главное — ясность и простота. Я начал готовиться к экзамену, сдам их вовремя. Очень полезно для решения этой проблемы! (Большое спасибо).

Многоугольники

Эта пунктирная область называется стороной многоугольника. AB, BC, CD, DE и EA (рис. 1) — стороны многоугольника ABCDE. Сумма всех сторон многоугольника называется его границей.

Многоугольник называется выпуклым, если одна из его сторон неограниченно выходит за пределы двух вершин.

Многоугольник MNPKO (рисунок 1) не является выпуклым, так как не лежит по одну сторону от линии CR.

Рассматриваются только криволинейные многоугольники.

Угол, образованный двумя соседними сторонами многоугольника, называется внутренним углом, а их вершины — вершинами многоугольника.

Линия, соединяющая две несмежные вершины многоугольника, называется диагональю многоугольника.

AC и AD — диагонали многоугольника (рис. 2).

Угол, примыкающий к внутреннему углу многоугольника, называется внешним углом многоугольника (рис. 3).

В зависимости от количества углов (сторон) многоугольники называют треугольниками, четырехугольниками, пятиугольниками и т.д.

Два многоугольника называются равными, если они могут пересекаться.

Вписанные и описанные многоугольники

Если все вершины многоугольника лежат на окружности, то многоугольник называется вписанным в окружность, а окружность — периметром (формой) многоугольника.

Если все ребра многоугольника касательны к окружности, то многоугольник называется кругом, а окружность — вписанной в многоугольник (рис.).

Подобие многоугольников

Два многоугольника с одинаковыми названиями называются сопряженными, если углы одного из них равны углам другого, а стороны многоугольника пропорциональны одной линии многоугольника.

Многоугольники с одинаковыми названиями называются многоугольниками с одинаковым количеством сторон (углов).

Грани подобных многоугольников называются симметричными гранями и соединяют вершины с соответствующими равными углами (рис.).

Так, например, чтобы сделать многоугольник ABCDE похожим на многоугольник A’B’C’D’E’, нам нужно сделать следующее ∠A=∠A’∠B=∠B’∠C=∠C’∠D=∠D’∠E=∠E’ и далее AB/_A’B’ = BC /_B’C’ = CD /_CD’ = DE /_D’E’ = EA /_E’A’Сначала рассмотрим свойства ряда равных отношений. Например, рассмотрим следующие отношения.

Отношение периметров подобных многоугольников

= 4 /₁ = 6 /₂ = 8 /₃ = 2.₄Если найти сумму предыдущих членов этих соотношений, затем найти сумму их последующих членов, затем найти отношение полученных сумм, то получим

То же самое происходит и при взятии других серий отношений. Например, 2 /

= 4 /₃ = 6 /₆ = 8 /₉ = 2.₁₂= 2 /₁₅ Нахождение суммы предыдущего члена и суммы следующего члена в этих соотношениях и нахождение отношения этих сумм дает следующее.₃В обоих случаях сумма предыдущих членов ряда равных отношений связана с суммой последующих членов того же ряда. Это то же самое, что предыдущий термин в этих отношениях связан со следующим термином.

Я придумал это свойство после рассмотрения некоторых числовых примеров. Она может быть выведена строго и в общем виде.

Далее мы рассмотрим пропорции вокруг таких многоугольников.

Предположим, что многоугольники ABCDE похожи на многоугольники A’B’C’D’E’ (рисунок).

Из сходства этих многоугольников следует, что

Основываясь на дифференциальных свойствах ряда равных отношений, мы можем написать

Поскольку сумма предыдущих членов полученных соотношений равна периметру первого многоугольника (P), а сумма последующих членов этих соотношений равна периметру второго многоугольника (P’), P /

P ‘_{= AB /}A’B’_A’B’Поэтому периметры подобных многоугольников связаны с подобными ребрами.

Пусть ABCDE и A’B’C’D’E’ — одинаковые многоугольники (рис.).

Отношение площадей подобных многоугольников

Второе отношение этих коэффициентов равно, что объясняется схожестью многоугольников.

Известно, что ΔAВС ~ ΔA’В’С’ ΔACD ~ ΔA’C’D’ и ΔADE ~ ΔA’D’E’.

Используя ряд свойств равных соотношений, мы имеем

где S и S’ — области этих одинаковых многоугольников.

Таким образом, области похожих многоугольников ассоциируются как квадраты с похожими сторонами.

Полученный тип может быть преобразован к следующей форме: S /

S ‘_{= (AB /}A’B’_{) 2}Вычислите площадь любого четырехугольника ABDC (рис.)

Площадь произвольного многоугольника

Нарисуйте диагонали. Пример: реклама. Есть два треугольника, ABD и ACD, и мы знаем, как вычислить их площади. Затем найдите сумму площадей этих треугольников. Эта сумма и есть площадь четырехугольника.

Если вам нужно вычислить площадь пятиугольника, сделайте то же самое: проведите диагонали из вершин. Вы получите три треугольника, площади которых можно вычислить. Таким образом, можно вычислить площадь конкретного пятиугольника. Сделайте то же самое, чтобы вычислить площадь любого многоугольника.

2. затем разделите полученную сумму на количество углов внутри. В примере с многоугольником предположим, что количество углов равно количеству ребер, т.е. равно 15. Все ли внутренние углы многоугольника равны 156?

Периметр многоугольника — это сумма длин его сторон.

Как найти периметр многоугольника и определить диагонали

Для четырехугольника ABCD периметр равен сумме его сторон: ab + bc + cd + da.

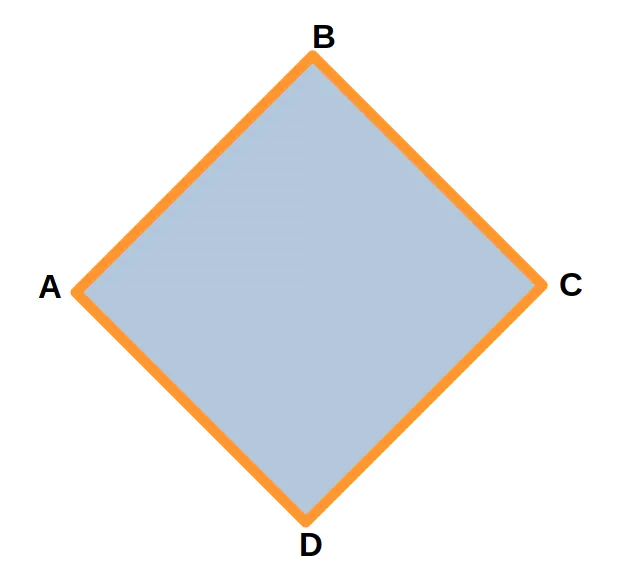
Задача: Длина одной стороны четырехугольника ABCD равна 3 см. Найдите периметр четырехугольного слоя.

Решение: ab + bc + cd + da = 3 + 3 + 3 + 3 + 3 + 3 = 12 см.

ОТВЕТ: периметр четырехугольника ABCD равен 12 см.

Диагонали многоугольника — это отрезки, соединяющие вершины противоположных углов.

Например, рекламная секция — это диагональ ABCDEF.

Свойства треугольника: если у треугольника нет углов с общими сторонами, то у него не может быть диагоналей.

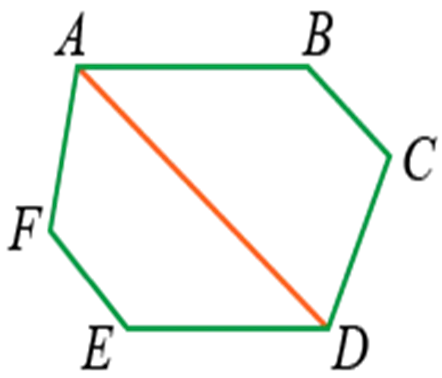
Если вершина проводит много диагоналей, фигура делится на много треугольников.

Число треугольников на 2 меньше числа сторон.

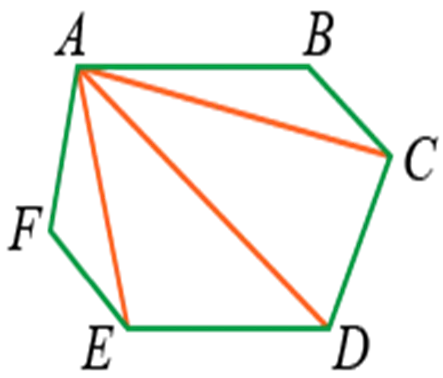
Если t — количество треугольников, а n — количество сторон, то вид: t = n — 2.

Деление многоугольника на множество треугольников с помощью диагоналей помогает быстро найти площадь.

Чтобы найти площадь многоугольника, разделите его на треугольники, найдите площадь этих треугольников и сложите результат.

Узнайте, как найти сумму углов выпуклого четырехугольника как по внешним, так и по внутренним углам. Но сначала давайте определим углы, называемые медиальными углами, выпуклого четырехугольника.

Сумма углов выпуклого многоугольника

Медиальные углы — это углы на смежных сторонах.

Например, ∠ABC — это внутренняя часть ABCDEF.

Внешние углы — это углы между одной стороной фигуры и линейным продолжением соседней части.

Например, ∠LBC — это внешний угол ABCDEF.

Правило: Сумма углов выпуклого многоугольника всегда равна количеству сторон. Это определение применимо ко всем углам.

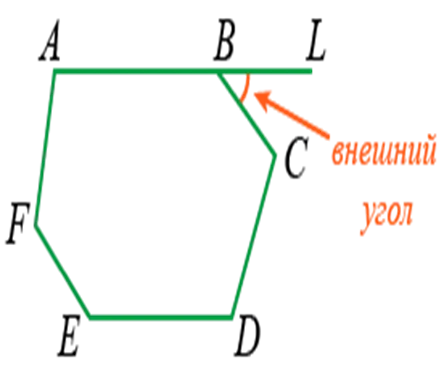
Это означает, что для нахождения количества углов достаточно измерить количество всех сторон. Поэтому сумма углов четырехугольника равна 4.

Правила нахождения суммы углов следующие Чтобы найти сумму всех медиальных углов выпуклого многогранного угла, умножьте количество сторон на 180° плюс 2.

Сумма внутренних углов

Символизм заключается в следующем.

Полигональный тип для нахождения суммы углов: s = 2d — (n — 2).

Сумму углов также можно найти, разделив фигуру на треугольники. Это равно сумме углов всех треугольников (180° — n).

Если фигура состоит из четырех треугольников, то сумма всех углов имеет вид: s = 2d(n — 2) = 180-4 = 720°.

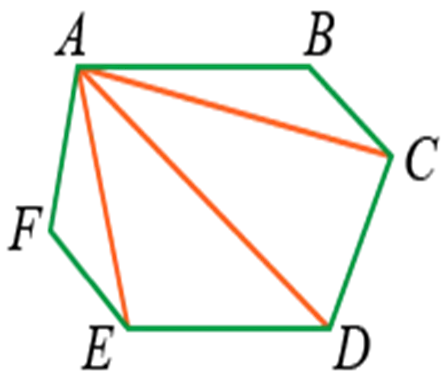
Это означает, что сумма внутренних углов является константой, которая зависит от количества сторон.

Правый многоугольник и круг регистрации/описания