Математики разработали целый алгоритм для сравнения первых двух дробей. Это позволяет сравнивать значения быстро и без ошибок. Чтобы приблизиться к ним, необходимо изучить смешанные числа.
Сравнение дробей
Мы продолжаем исследование дробей. Сегодня мы поговорим об их сравнении. Эта тема интересна и полезна. Это позволит новичкам почувствовать себя учеными в белых халатах.
Суть сравнения дробей заключается в том, чтобы выяснить, какая из двух дробей больше или меньше.
Чтобы ответить на вопрос, какая из двух дробей больше или меньше (>) или меньше (>)<).
Математики заботятся о том, чтобы предоставить готовые правила для быстрого ответа на вопрос, больше или меньше дробь. Эти правила можно смело применять.
Посмотрите на все эти правила и попытайтесь понять, почему так происходит.
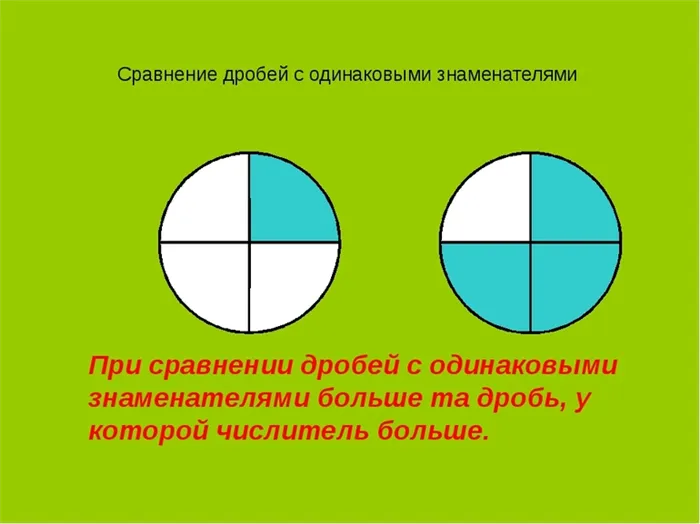
Сравнение дробей с одинаковыми знаменателями
Сравниваемые дроби — это все виды дробей. Наилучший вариант — когда знаменатели дробей одинаковые, а числители разные. В этом случае действуют следующие правила
Из двух дробей с одинаковыми знаменателями дробь с наибольшим числителем будет больше. Дробь с наименьшим числителем будет меньше.
Например, сравните дроби и ответьте, какая из них больше. Знаменатели одинаковые, но числители разные. Числитель дроби больше, чем Дробь больше, чем дробь больше. Вот наш ответ. Для ответа на вопрос используйте символ заглавной буквы (>).
Этот пример можно легко понять, если учесть, что пицца делится на четыре части.
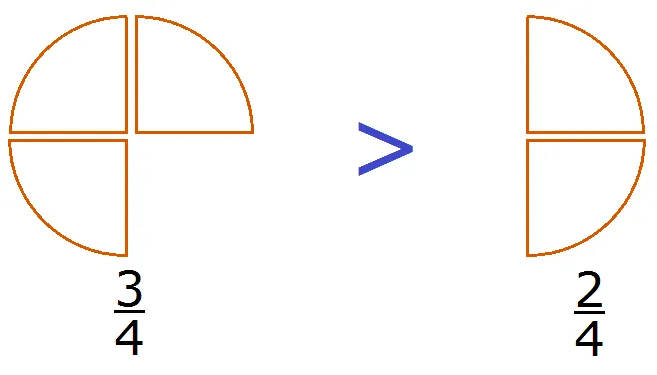
Все согласятся, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителями
Следующий случай — когда числители у дробей одинаковые, а знаменатели разные. В этих случаях предусмотрены следующие правила
Из двух дробей с одинаковым числителем дробь с наименьшим знаменателем больше. Тот, у которого наибольший знаменатель, меньше.
Сравните, например, дроби с. У этих дробей одинаковый числитель. Знаменатель дроби меньше. Дробь имеет больший знаменатель. Вот ответ: дробь больше знаменателя дроби.
Этот пример можно легко понять, рассмотрев пиццу, разделенную на три и четыре доли. Пиццы больше, чем пиццы:.

Все согласятся, что первая пицца больше, чем вторая.
Проверка второго и третьего пунктов методологии имеет большое значение. Это связано с тем, что данные меры помогают избежать многих ошибок при выполнении операций сравнения дробей обычного типа.
Сравнение дробей с равными числителями.
Если числители дробей одинаковы, то дробь с меньшим знаменателем будет больше.
Вы можете понять правило, приведя примеры из жизни, например. Есть торт. Доступно для 5 или 11 человек. Для 5 гостей торт делится на 5 равных порций; для 11 гостей торт делится на 11 равных порций. Теперь рассмотрим случай, когда у гостей есть торт большего размера. Конечно, когда придут пять гостей, торт будет больше.
Или другой пример. Есть 20 конфет. Вы можете отдать конфеты поровну четырем друзьям или разделить конфеты поровну между десятью друзьями. В таком случае, у каждого ли друга больше конфет? Конечно, если вы поделитесь конфетами с четырьмя друзьями, у каждого друга будет больше конфет. Давайте рассмотрим эту проблему математически.
Решение этих дробей дает числа ǫ (ǫ frac = 5 \) и ǫ (ǫ frac = 2 \). Другими словами, 5>2.
Это правило для сравнения дробей с одинаковым числителем.
Сравните дроби с одинаковым числителем ⌘ (⌘ frac \) и \ (⌘ frac \).
Поскольку числители одинаковы, знаменатели больше в наименьшем знаменателе.
Сравнение дробей с разными знаменателями и числителями.
Чтобы сравнить дроби с разными знаменателями, их необходимо привести к общему знаменателю, прежде чем сравнивать числители.
Сравните доли \ (\ frac \) и \ (\ frac \).
Сначала найдите общий знаменатель дробей. 21.
Затем сравните числители. Правила сравнения дробей с одинаковыми знаменателями одинаковы.
Сравнение неправильной и правильной дроби.
Неправильные пропорции всегда больше, чем нормальные. Это происходит потому, что неправильная пропорция больше 1, а правильная пропорция меньше 1.
Пример: сравните дроби \(\ frac \) и \(\ frac \).
Дробь ⌘ (⌘ frac \) неверна и больше 1.
Дробь ⌘ (⌘ frac \) верна и меньше 1. Сравнение:.
Смежный вопрос: как можно сравнить дроби с разными знаменателями? ОТВЕТ: Необходимо привести дроби к общему знаменателю, а затем сравнить их числители.
Как можно сравнивать дроби? ОТВЕТ: Сначала нужно определить, к какой категории относятся дроби. Необходимо определить, является ли знаменатель общим, числитель общим, знаменатель и числитель не являются общими, а также являются ли дроби правильными или неправильными. После сортировки дробей примените соответствующие правила сравнения.
Что такое сравнение дробей с одинаковым числителем? ОТВЕТ: Если числители дробей одинаковы, то дробь с наименьшим знаменателем будет больше.
Пример 1: Сравните дроби \ (\ frac \) и \ (\ frac \).
Решение: применяются правила сравнения с разными знаменателями, так как числители и знаменатели не одинаковы. Необходимо найти общий знаменатель. Общий знаменатель — 96. Сократите дроби до общего знаменателя. Умножьте первую дробь \ (\ frac \) на дополнительный коэффициент 8 и умножьте вторую дробь \ (\ frac \) на 6.
Сравните дроби по числителю; укажите, у какой из двух дробей числитель больше.
Пример 2: Какая дробь равна 1?
Решение: каждая нормальная пропорция всегда меньше единицы.
Проблема №1: Сын и его отец играли в футбол. Сын забил пять раз из десяти попыток. И отец попал в ворота три раза из пяти стрел. Какой результат был лучше?
Решение: сын попал по мячу пять раз из десяти попыток. Опишите это как дробное dž (dž frac dž). Отцу удалось 3 из 5 попыток. Запишите это в виде дроби ⌘ (⌘ frac \).
Сравните дроби. Поскольку числитель и знаменатель разные, сравните их с одним и тем же знаменателем. Общий знаменатель равен 10.
Ответ заключается в том, что отцы добиваются лучших результатов.
You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.
Деление дробей. Правила. Примеры.
Добавить комментарий Отменить ответ.
Вы должны войти в систему, чтобы оставить комментарий.
Математики заботятся о том, чтобы предоставить готовые правила для быстрого ответа на вопрос, больше или меньше дробь. Эти правила можно смело применять.
Сравнение дробей с разными числителями и разными знаменателями
Сравнение дробей с одинаковыми числителями или знаменателями не представляет сложности. Сравнение неравных дробей требует немного больше усилий.
Чтобы сравнить дроби с разными знаменателями, нужно привести их к общему знаменателю, а затем сравнить числители.
Сначала вспомним, как приводить дроби к общему знаменателю. Рассмотрим пример дробей с разными знаменателями.
Практикуйтесь в сравнении дробей.
Пример 1. Сравнение дробей:.
При сравнении неправильных и правильных дробей обратите внимание на то, что неправильная дробь всегда больше правильной.
Пример 2: Сравнение дробей:.
Вычитание смешанных чисел
Если удаляемое больше удаляемого, то вычитание проходит гладко.
Если вычеты больше, чем изъятия, то разница будет отрицательной. В этом нет ничего плохого. Однако математика пятого года обучения является «позитивной», поэтому научитесь находить разность между смешанными числами без «негатива».
Те же принципы применяются при удалении фракций. Вывозимого имущества должно быть меньше, чем вывозимого. Именно здесь пригодится умение сравнивать дроби.
Пример 1. Расчет.
Удаляемая фракция меньше удаляемой фракции.
Пример 2: Нахождение разницы:.
Примеры для самопроверки
Конечно, теория — это хорошо. Но вы не сможете сделать это без практики. Пришло время попрактиковаться в примерах и конкретизировать проблему сравнения дробей.
Пример 1. Сравнение дробей:.
ОТВЕТ: согласно правилу сравнения дробей с одинаковыми знаменателями, доля с большим числителем будет больше. Это означает следующее.
Пример 2.Сравнение дробей:.
ОТВЕТ: согласно правилу сравнения дробей с разными знаменателями или равными числами, дробь с меньшим знаменателем больше. Что это значит.
Мы получили дроби, содержащие разные числители и разные знаменатели. Чтобы сравнить такие дроби, нужно привести их к одному знаменателю. Как это сделать, подробно не объясняется. Если на этом этапе у вас возникнут трудности, убедитесь, что вы научились работать с дробями.
Единый знаменатель

Сравнение двух обычных дробей с разными знаменателями — непростая задача. Преобразование их в единую цену требует знания специальных методик.
Они были подробно изучены в пятом классе. Всего есть три случая, когда применяется тот или иной тип алгоритма.
- Знаменатель одной дроби «g» делится на другой «m» c образованием целого значения.
- Величина «g» cодержит одинаковые множители с «m».
- Другой случай.
Один из них считается очень простым. Это объясняется тем, что для получения коэффициента достаточно разделить одно значение на другое. Во втором случае необходимо найти наименьшее общественное кратное (LCC), а в третьем — просто умножить знаменатель, но с некоторой спецификой. Каждая из этих трех ситуаций должна рассматриваться отдельно, поскольку они требуют использования совершенно разных методов.
Деление нацело
Преобразование дробей с разными знаменателями производится в простой форме, при этом один знаменатель делится на другой. Следующее:.

- Записать две величины: 2 (5/6) и 1 (9/12).
- При необходимости преобразовать их в неправильные дроби: 17/6 и 21/12.
- Вычислить коэффициенты при числителях: для первой — 12/6=2, для второй — 12/12.
- Выполнить математические операции: 17*2/12=34/12 и 21/12.
Обратите внимание, что берется наибольший знаменатель. Это одинаково для всех дробных выражений. Кроме того, перед поиском всегда рекомендуется преобразовывать числа в неправильные пропорции. Это связано с трудностью выполнения математических действий.
Однако бывают случаи, когда включается общий множитель, но значение делится на остаток. Для этого следует рассмотреть следующие случаи.
Одинаковые сомножители
Один из самых сложных случаев — когда все знаменатели имеют общий множитель. Для этого необходимо определить величину, которую нужно разделить на один и другой знаменатель. Это названо самым низким зрителем в математике. Чтобы найти его, этот алгоритм нужно использовать, например, с двумя числами 12 и 16.
- Разложить каждое из них на множители: 12=2*2*3 и 16=2*2*2*2.
- Найти повторяющиеся элементы: 2*2.
- Умножить их на компоненты, которые являются разными для двух чисел: 2*2*(3*2*2)=48.
После нахождения NOC дробное значение уменьшается в соответствии с определенным алгоритмом. Следующее:.
- Разделить НОК на каждый из знаменателей, записав над числителями определенные коэффициенты.
- Выполнить математические преобразования.
- Записать искомые результаты.
На практике необходимо понять все возможности применения алгоритма. Это выглядит следующим образом:.
Сравнение обыкновенных дробных выражений
Для сравнения двух математических величин используется рациональное действие, обозначаемое символом ‘>’. Его «острый» элемент направлен в сторону наименьшего значения, т.е. 4/8> 1/8. Сравнение дробей в обычной форме G/F и S/T очень просто. Для этого необходимо решить три случая, показанные в математике Фон.

- Параметры «g» и «s» эквивалентны между собой, значения «f» и «t» отличаются.
- Величины «f» и «t» эквивалентны между собой, а значения «f» и «t» неодинаковы.
- Числители и знаменатели являются разными числами.
- Одна дробь меньше нуля, а другая — больше.
В первом случае нет необходимости приводить дроби к общему знаменателю. Достаточно использовать правило. Если числа одинаковые, а знаменатели разные, то одна дробь будет больше другой, а знаменатель будет меньше. Это правило экономит время.
В последнем случае также существуют специальные правила, которые позволяют определить наибольшее значение без математических преобразований. Это происходит следующим образом. Если числители не равны друг другу, а знаменатели равны, то дробное значение с наибольшим числителем будет больше других значений.
Метод, используемый в приведенном выше случае, называется взаимным определением, так как он не требует выполнения различных преобразований чисел. Если все элементы общей дроби не равны друг другу (ни числитель, ни знаменатель), то перед выполнением второго типа взаимосравнения необходимо использовать один из алгоритмов для приведения дробного выражения к общему знаменателю.
Обратите внимание, что очень легко сравнивать положительные и отрицательные значения, так как последнее всегда меньше первого.
Таким образом, сравнение дробей выполняется по определенной методике, но для того, чтобы приступить к нему, необходимы базовые знания в области преобразования смешанных чисел и вычисления наименьших общих знаменателей.
Однако этого недостаточно для сравнения дробей с разными знаменателями. Затем необходимо рассмотреть методы, позволяющие свести их к общей форме.
Сравнение смешанных и неправильных дробей с правильными дробями
Неправильные или смешанные дроби всегда больше, чем нормальные. Далее приводится пример.
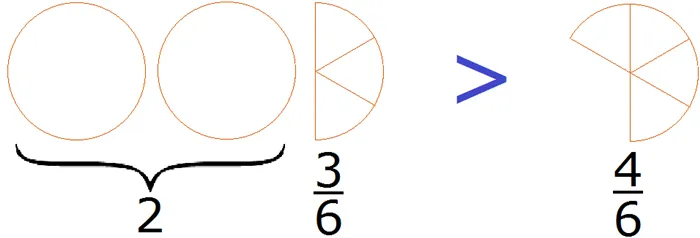
Это правило основано на том, что смешанные или неправильные дроби (которые всегда можно преобразовать в смешанные путем разделения целых частей) уже содержат одну или более единиц (целых частей), в то время как обычные дроби всегда меньше единицы.
Сравнение двух смешанных дробей
При сравнении двух смешанных дробей, дробь с большей целой частью имеет вид

Если смешанные дроби имеют одинаковое целое число, то дробь с большей дробью больше. Далее приводится пример.

Чтобы понять, представьте ситуацию, когда торт нужно разделить между тремя друзьями. Это означает, что шесть пирожных делятся поровну между тремя людьми. С двумя частями для каждого, 6:3 = 2.
Что такое дробь?
Дробь — это несовершенный акт деления. В практических расчетах часто не удается разделить число с помощью десятичных дробей. С другой стороны, такие операции можно записать в виде дробей и продолжить вычисления без потери точности.
Если одно число нельзя разделить на другое, результат можно округлить. Однако округлять стоит только конечный результат вычисления, так как при этом теряется точность расчета.
Частные случаи сравнения дробей
Рассмотрим сравнение некоторых конкретных фракций.
- Если у дробей знаменатели равны, то больше та дробь, числитель которой больше.
- Если у дробей равны числители, то больше та дробь, знаменатель которой меньше.
- Если числители и знаменатели дробей равны, то и такие дроби равны.
Обратите внимание, однако, что в результате вычислений могут получиться дроби, у которых числитель равен нулю. В таких случаях общая дробь равна нулю, и дробь следует немедленно преобразовать в ноль. Однако знаменатель не может быть нулевым.








