Смежные углы — это два угла с общей вершиной и одним ребром, причем два других ребра входят друг в друга и лежат на одной прямой.
Смежные и вертикальные углы
Смежные углы — это пара углов, у которых одно ребро общее, а два других ребра лежат на одной прямой. Поэтому два соседних угла образуют развернутый угол. Общее ребро двух смежных углов называется наклонной к прямой, на которой расположено другое ребро (только если смежные углы не равны).
∠Углы ABD и BCDBC — смежные углы, AC — прямая линия, радиус BD — общая сторона угла и наклонена к линии AC, BCABC — угол расширения, B — основание наклонного угла.
Чтобы построить касательную к заданному углу, нужно продлить одну из сторон угла за пределы вершины.
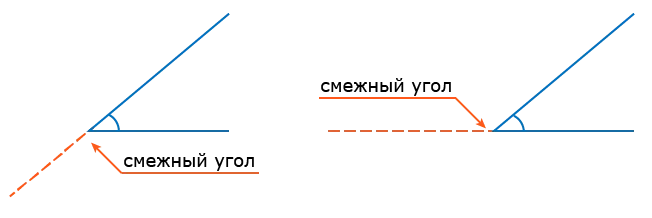
Равенство вертикальных углов
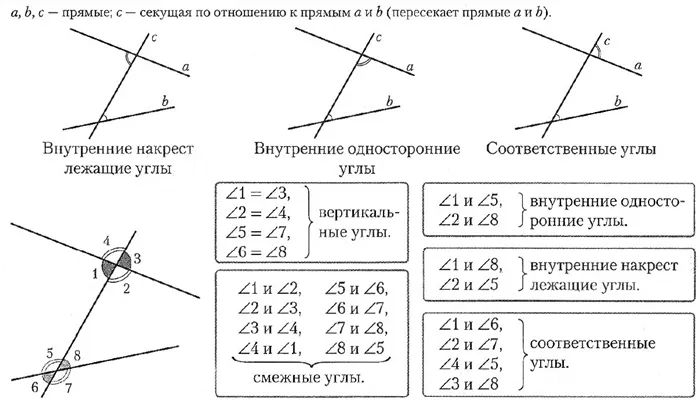
Углы вершин равны друг другу. Рассмотрите вершинные углы 1 и 3.
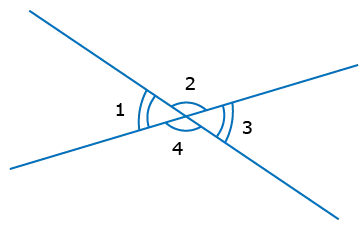
∠ Сумма углов 1 и 2 равна углу продолжения (180°). Сумма ∠2 и .3 также равна углу разворота (180°). Хорошо.
∠1+∠2=∠2+∠3
Следовательно, ∠1=.3. Докажите, что углы при вершинах равны.
Также называются импликациями или тригонометрическими соотношениями. Они основаны на теореме косинусов этих фигур и на том факте, что размеры касательных всегда одинаковы, но противоположны по знаку. Если угол необходимо построить рядом с существующим углом, одна из сторон должна выходить за пределы вершины.
Свойства и виды смежных углов в геометрии
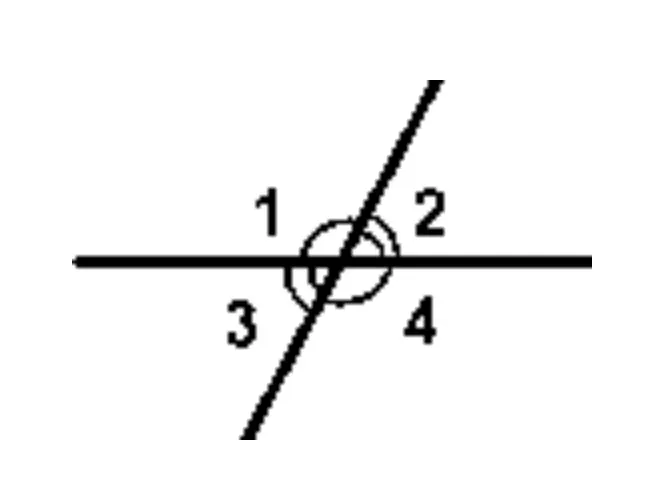
- Так как две стороны смежных углов образуют прямую линию, то вместе они составляют развернутый угол. Его градусная мера составляет 180^\circ. Следовательно — сумма смежных углов тоже равна \(180^\circ.\)
- Если две прямые пересекаются, то они образуют две пары смежных углов: \(\angle1\) и \(\angle2\), \(\angle3\) и \(\angle4\), а также \(\angle1\) и \(\angle3\), \( \angle2\) и \(\angle4\). При этом объединение пар, которые обозначены обозначениями 1 и 4, 2 и 3, представляют из себя вертикальные углы, а значит — они равны. Поэтому рассматривать можно только одну из пар смежных углов, другая окажется идентична по всем показателям.
- У смежных углов одинаковые синусы.
- Для косинусов и тангенсов тоже распространяется равенство, но их значения противоположны по знаку.
- Чтобы построить смежный угол уже заданному, требуется продлить одну из сторон существующего угла дальше вершины.
В парах действует правило: если один угол тупой, то другой обязательно будет острым.
Если один из углов правильный, то второй тоже правильный.
Внимание! Если преподаватель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до исключения). Если вы не можете написать работу самостоятельно, вы можете заказать ее здесь.
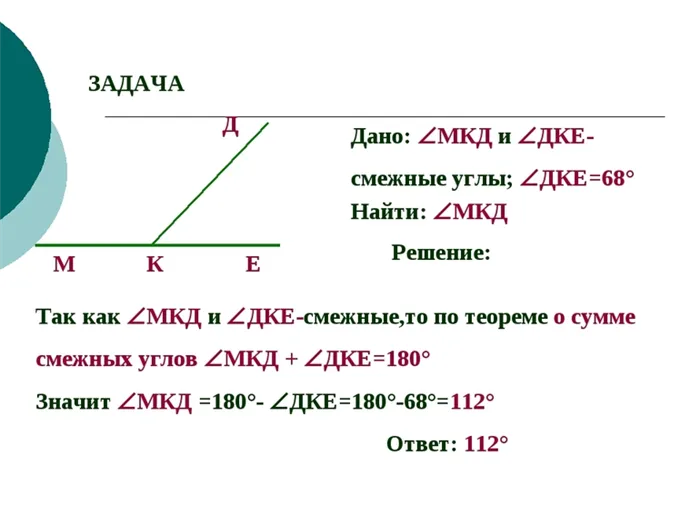
Дано: \(\ угол \ альфа \) и \(\ угол \ бета \) смежны друг с другом и \(\ угол \ бета = 60 ^ \ окружность \).
Поиски: что такое \(\ угол ⌘ альфа ⌘)?
Если углы смежные, то
Ans: \(\;\ угол \альфа = 120 ^ \ круг \).
Дано: \(ዄ;ዄ угол \ альфа \) и \(ዄ;ዄ угол бета \) смежные и \(ዄ;ዄ угол \ альфа \) больше, чем \(ዄ;ዄ угол бета.ዄ) больше, чем \(30 ^ \ circ \).
Поиск: чему равны \(\ угол \ альфа) и \(\ угол \ бета. \)?
\При условии, что ዄ (ዄ угол \ бета = x \), то ዄ (ዄ угол \ альфа = x + 30 ^ \ окружность ዄ).
Поскольку сумма смежных углов равна 180 градусам, получаем следующее уравнение
Следовательно, значение 섹 (섹 угол \ бета = 75 ^ \ круг. 섹)
Для того чтобы найти значение \ (\ угол \ альфа \), необходимо произвести обычные вычисления по теореме о сумме.
Вторая индустриализация России — это совокупность научных, технических и других инновационных идей, планов и разработок, которые могут быть широко применены в практике хозяйственной деятельности в короткий срок (3-5 лет) и обеспечивают качественно новые прогрессивные сдвиги. общества в ближайшие 50-75 лет.
Интересный факт
Связь между математикой и музыкой.
‘Учитывая искусство и науку, их взаимосвязи и противоречия, мы приходим к выводу, что математика и музыка находятся на крайних полюсах человеческой психики. Человечество было создано в области науки и искусства». Х. Нейгауза кажется очень абстрактной областью математики. Однако связь между математикой и музыкой исторически и внутренне зависима, несмотря на то, что математика является наиболее абстрактной наукой и музыкой. Соглашение было основано на этой музыкальной системе, которая определяла приятное звучание струны, и двух законах, названных в честь двух великих ученых — Пифагора и Архетипа. Эти законы таковы: 1. Если две звуковые струны ассоциируются как целые числа по длине, определяют согласие и образуют треугольное число 10 = 1+2+3+4, т.е. 1:2, 2:3, 3:4. Более того, чем меньше число n в соотношении n: (n+1) (n = 1,2,3), тем более созвучны получаемые интервалы. 2. Частота колебаний w звуковой струны обратно пропорциональна длине L. w = a:l, где a — коэффициент, характеризующий физические свойства струны.
(Мы также предлагаем забавную пародию на двух математиков, которые не согласны =)
Геометрия вокруг нас
Геометрия играет важную роль в нашей жизни. Оглянувшись вокруг, вы заметите, что нас окружают различные геометрические фигуры. Мы видим их повсюду: на улице, в классе, дома, в парке, в спортзале, в школьной столовой — в общем, везде, куда бы мы ни пошли. Но тема сегодняшнего урока — соседний уголь. Поэтому давайте осмотримся и найдем уголок в этой среде. Если вы внимательно посмотрите через окно, то увидите, что ветви некоторых деревьев образуют смежные углы, а на портальной перегородке можно увидеть множество вертикальных углов. Приведите собственные примеры смежных углов, которые вы заметили в окружающей среде.
1. это книга на столе в книжной базе. Какой угол он образует? 2.Это студент, работающий на ноутбуке. Какой здесь угол? 3. какой угол образует фоторамка на основании? 4. как вы думаете, могут ли два смежных угла быть равными?
Перед вами появляется геометрическая фигура. Как он выглядит и как вы его называете? Назовите все смежные углы, которые вы видите в этой геометрической фигуре.
Перед вами картинка и картинка с картинкой. Рассмотрите их внимательно и скажите, какой угол изображен на рисунке и какой угол на рисунке.

Решение задач
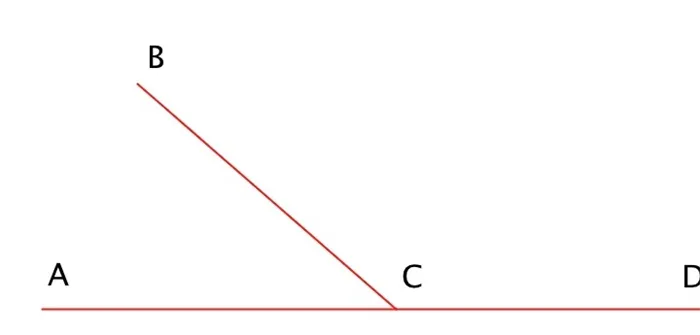
1. сумма трех углов, образованных пересечением двух рядов, равна 100°? 370°; 2. Найдите все пары смежных углов на изображении. Теперь вертикальные углы. Назовите эти углы.
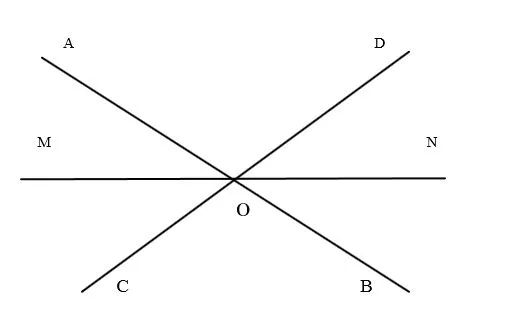
3. найдите угол, если он в три раза больше соседнего угла. 4. две прямые линии пересекаются. Этот перекресток вел к четырем углам. Определите их размеры по следующим признакам.
a) сумма двух из четырех углов равна 84° — b) разность двух из углов равна 45° — c) один угол в четыре раза больше другого. °.
При планировании легче решать проблемы, связанные с конкретными вопросами. С их помощью и знанием их качеств и теорем найти правильный ответ не составит труда. Есть типовые упражнения, которые помогут закрепить полученные знания и применить их в своей практике. Одними из наиболее интересных решений такого рода являются
Смежные углы и их свойства
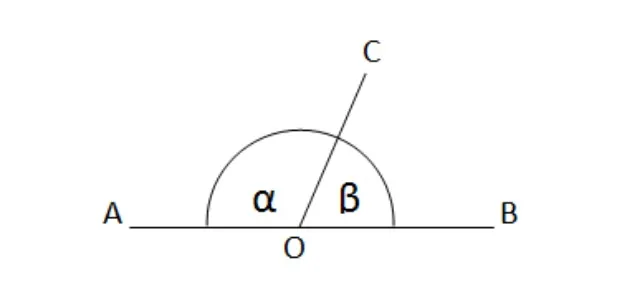
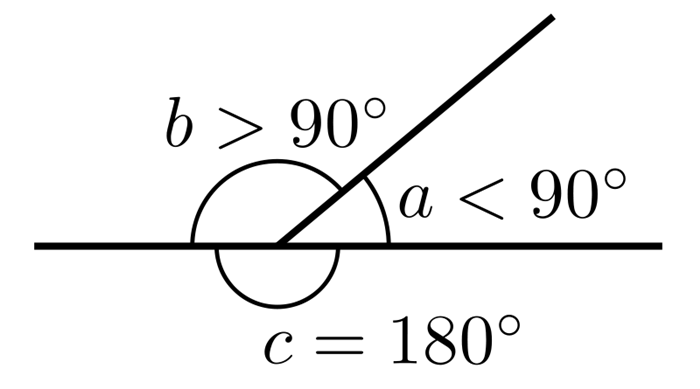
Смежные углы — это два угла, у которых одна сторона общая, а две другие стороны смежные и лежат на одной прямой.
Смежные углы (понятие и определение):
Смежные углы — это два угла, у которых одна сторона общая, а две другие стороны дополняют друг друга и лежат на одной прямой. Поэтому все смежные углы вместе образуют открытый угол.

Расширенный угол — это угол 180°.
Таким образом, сумма значений смежных углов равна 180°.
Значение угла β, касательного к углу α, равно (180°-α) градусов.
Свойства смежных углов:
1. сумма размеров смежных углов равна 180°.
2. пересечение двух прямых дает две пары смежных углов.
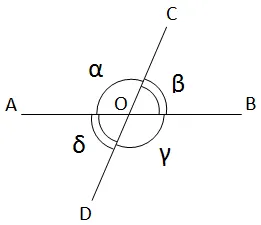
3. углы, касательные к прямому углу, являются прямыми углами. Эти углы равны между собой.

4.В паре смежных углов один угол всегда тупой, а другой всегда острый или оба угла прямые.
5. синусоиды смежных углов равны.
6. теорема косинуса и тангенсы смежных углов имеют одинаковую величину, но противоположные знаки.
Примечание: © Фотографии https: /www.pexels.com, https: /pixabay.com
Мировая экономика
Справочники
Востребованные технологии
- Концепция инновационного развития общественного производства – осуществления Второй индустриализации России на период 2017-2022 гг. (106 945)
- Экономика Второй индустриализации России (103 199)
- Этилен (этен), получение, свойства, химические реакции (29 510)
- Программа искусственного интеллекта ЭЛИС (29 469)
- Метан, получение, свойства, химические реакции (26 571)
- Крахмал, свойства, получение и применение (26 035)
- Природный газ, свойства, химический состав, добыча и применение (25 163)
- Целлюлоза, свойства, получение и применение (24 308)
- Пропилен (пропен), получение, свойства, химические реакции (23 556)
- Прямоугольный треугольник, свойства, признаки и формулы (23 269)
Поиск технологий
О чём данный сайт?
Сайт посвящен научным разработкам автора в области экономики и научным идеям осуществления второй индустриализации России.
Включает:- Экономика второй индустриализации России — Теории, методологии и инструменты инновационного развития — Реализация второй индустриализации России — Организационные механизмы второй индустриализации России — Справочник по инновационным технологиям.
Продукты и технологии не продаются. Производители и изобретатели! Вы должны связаться с ними напрямую!
Мы ведем переговоры с отечественными производителями и изобретателями инновационных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Применение второй индустриализации в России базируется на качественно новых научных основаниях (теория, методология и инструментарий), разработанных авторами.
Конечным результатом второй индустриализации России является рост благосостояния всех членов общества — среднего человека, предприятия и государства.
Вторая индустриализация России — это совокупность научных, технических и других инновационных идей, планов и разработок, которые могут быть широко применены в практике хозяйственной деятельности в короткий срок (3-5 лет) и обеспечивают качественно новые прогрессивные сдвиги. общества в ближайшие 50-75 лет.
Россия, первой сделавшая это сложное открытие, станет лидером мирового сообщества, что в других странах останется невозможным в течение столетий.
Проблема может быть решена, если вместо градуса и радиуса значения нижнего угла дать отношение нижнего угла к смежным углам. В этом случае решение похоже на уравнение с коэффициентами.
Примеры решения задач
При планировании легче решать проблемы, связанные с конкретными вопросами. С их помощью и знанием их качеств и теорем найти правильный ответ не составит труда. Есть типовые упражнения, которые помогут закрепить полученные знания и применить их в своей практике. Одними из наиболее интересных решений такого рода являются

- Возможно ли существование такой смежной пары, в которой будут два остроугольника? Для ответа на вопрос нужно рассуждать следующим образом. Острым называется такой элемент, разворот которого меньше 90 градусов. Так как пара должна содержать общую сторону, то второй элемент будет тупоугольным. Исключением будет, если из вершины лучи выходят перпендикулярно друг другу, поэтому существование такой пары невозможно.
- Один из парных элементов меньше другого на 80 градусов, необходимо найти разворот второго. Итак, если первый угол принять равным U, то второй, согласно условию, будет равняться U — 80. Так как в сумме они оба дают 180 градусов, то верным будут следующие уравнения: U + U + 66 = 180; 2 * U = 180 — 80; 2 * U = 100; U = 100/2 = 50. Отсюда разворот второго элемента составит: 50 + 80 = 130 градусов.
- Имеются два прямоугольных треугольника со смежными между собой углами, при этом их меры в градусах относятся как 2:3. Чтобы найти их значения, нужно вспомнить, что сумма смежных углов равна 180 градусам. Обозначив первый разворот два икс, а второй с коэффициентом три, справедливо будет записать: 2x + 3x = 180. Решив уравнение, можно определить икс, его значение будет равняться: x = 30. Затем, подставив вместо икса его численную величину, довольно просто вычислить ответ. Искомые значения будут 60 и 90 градусов.
- Восьмая часть одного из смежных элементов и три четверти другого составляют в сумме прямую фигуру. Нужно найти разность. Так как сумма парных углов 180°, то пусть один из них равняется икс, тогда другой будет игрек. На основании этих данных можно составить систему: x + y = 180; x / 8+ (3у) / 4 = 90. Сложив оба уравнения, можно получить равенство: x + 6y = 720; 5y = 540. Отсюда: y = 108°, x = 180 — 108 = 72 градуса. В итоге искомая разность составит: 108 — 72 = 36.
Важно уметь правильно решить задачу, потому что позже эти знания помогут вам найти такие важные элементы, как площадь треугольника, а вы будете знать только протяженность и высоту любой заданной фигуры. Таким образом, вычисление объема становится проще. Кроме того, правила окрестности часто используются в тригонометрии для нахождения синуса и косинуса.
Вычисление на онлайн-калькуляторе
Нахождение меры степени смежных элементов обычно не представляет проблемы и является одним из основополагающих действий при изучении различных треугольников. Кислород или равнобедренные треугольники. Однако при оперировании нецелыми числами или обучении имеет смысл использовать так называемые онлайн-калькуляторы.
Обычно это веб-сайты, содержащие программы для автоматических расчетов. Ими может воспользоваться любой человек, имеющий компьютер или гаджет с установленным интернет-браузером. Вся работа с сервисом сводится к загрузке сайта и заполнению специальной формы, куда вы вводите свои исходные данные. Затем нажимается интерактивная кнопка, и ответы появляются на экране.

Расчеты обычно занимают несколько секунд, и ошибки исключены. Кроме того, сайты, предлагающие подобные услуги, включают весь теоретический материал, необходимый для расчета. Таким образом, даже осторожные пользователи могут понять, где и как он приходит к ответу.
Среди многочисленных сервисов в русскоязычном разделе Всемирной паутины можно отметить следующие.
Эти услуги предоставляются бесплатно и имеют интуитивно понятную рабочую среду на русском языке.
В то же время пользователям предоставляется возможность ознакомиться с подробными решениями, т.е. пошаговыми расчетами. Для удобства на страницах представлена не только необходимая теория, но и типичные примеры с подробным описанием действий.
Следует отметить, что вышеперечисленные сервисы можно использовать для поиска ответов на сложные математические задачи. Такие расчеты в технике, связанные с тригонометрическими функциями, являются особенно сложными. В конце концов, в таких расчетах важны точность и время, которые компьютеры могут обеспечить очень хорошо.
Ключевые слова контура: угол, биссектриса, угол, измерение угла, смежные и перпендикулярные углы, смежные и перпендикулярные углы, угол пересечения двух линий.
Свойства смежных и вертикальных углов

Геометрия углов Заметки по курсу. ‘Смежные и перпендикулярные углы’. Использовались экстракты с семинара.
- Александр Роганин: Геометрия в схемах, терминах, таблицах / Ростов-на-Дону: Издательство ФЕНИКС,
- Евгений Нелин: Геометрия. 7-11 классы. Определения, свойства, методы решения задач — в таблицах / Москва: Издательство ИЛЕКСА,
- Анжелика Мещерякова: Геометрия. 7 класс. Опорные конспекты / Минск: Издательство АВЕРСЭВ,
- Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.: Геометрия. 7—9 классы: учеб. для общеобразоват. организаций / Москва: Просвещение.
Указанное пособие предполагается использовать в учебных целях, со ссылкой на письменные, заемные источники и ссылки на рынок пособий в крупнейшем магазине электронных книг (ст. 1274, ст. 1274 ГК РФ). Выберите следующие шаги.








