Тот факт, что между пирогом \(ɛ displaystyle 5 \) и пирогом \(ɛ displaystyle 2/3 \) нет знаков, не означает, что есть знаки умножения, как при записи ɛ displaystyle 2x. (\ ⌘⌘ ⌘ ⌘ ⌘ ⌘ ⌘ ⌘ ⌘ ⌘ ⌘).
Обыкновенные дроби
Число a называется числителем, а число b — дробным знаменателем.
При умножении или делении числителя и знаменателя на одно и то же число получаются равные дроби.
Пример 1. В первой пропорции при делении числителя и знаменателя на одинаковое число 14 единиц получаются равные дроби. В качестве альтернативы во второй пропорции числитель и знаменатель можно умножить на одно и то же число. 5.
- Сократимые – это дроби, у которых числитель и знаменатель делятся на одно и то же число.
- Несократимые – это дроби, у которых числитель и знаменатель не имеют общих делителей.
Уменьшение дроби — это деление числителя и знаменателя на одно и то же число.
Пример 2: Чтобы сократить определенную дробь, вспомните понятие деления и обратите внимание, что поскольку числитель и знаменатель являются весами, их можно разделить на 2. Это означает, что дробь увеличивается на 2.
Пример 3: Согласно принципу деления, дробь уменьшается на 5, так как числитель и знаменатель делятся на 5.
При сложении (вычитании) дробей с одинаковым знаменателем сохраняйте знаменатель неизменным и прибавляйте (вычитайте) числитель. При смешивании дробей добавляйте (удаляйте) целые части по отдельности.
Решения можно кратко описать словесным сложением или удалением целых и дробных чисел.
Вычитание обыкновенной дроби из целого числа
Чтобы удалить дроби из единицы, необходимо преобразовать единицу в неправильные дроби с помощью числителей и знаменателей и удалить дроби.
Пример 5. Чтобы представить единицу в виде дроби, отнимите дроби с одинаковыми знаменателями (числитель можно отнять устно).
Если вам нужно отнять число, большее 1, вы должны представить дробь в виде смешанного числа, где в числителе и знаменателе также отнимаются дроби, равные знаменателю.
Сложение и вычитание дробей с разными знаменателями
Чтобы складывать и вычитать дроби с разными знаменателями, дроби сначала нужно привести к общему знаменателю. Существует несколько методов, которые можно использовать для нахождения общего знаменателя
Нахождение общего знаменателя
Наименьшее общественное кратное (LSN) — это наименьшее число, которое можно разделить без остатка на заданный знаменатель. Обычно его можно найти устно, выполнив действие с использованием дробей.
Правило нахождения произведения дробей дано на примере чисел 12 и 15. Пример №7: 1. Каждое число сначала нужно разделить на множители.
2. затем найдите тот же множитель (подчеркнутый).
В данном случае это только множитель 3.
3.Возьмите одно из данных чисел и умножьте его на другой (неоплаченный) множитель другого числа.
12 на 5: 12 x 5 = 60, или
15 x 2 и 2: 15 x 2 x 2 = 60.
Таким образом, noc = 60. Обычно достаточно внимательно посмотреть на числа и найти их Noq в уме.
Распространение знаменателя. Техника №2.
Просто умножьте знаменатель. Обычно этот метод используется, когда дано первое число (делится на 1 и само на себя) и не может быть разложено на множители.
Пример №8.
Чтобы найти общий знаменатель в первом случае: 17 x 19 = 323, во втором: умножение 11 и 13 дает 143.
Последовательные отборы. Метод №3.
Этот метод может быть применен устно к небольшому числу людей. Возьмите наибольший знаменатель и умножьте на 2, чтобы это число делилось на второй знаменатель. Если нет, умножьте последовательно на 3 и 4 и проверьте таким же образом.
Пример №9. возьмите число 51, умножьте на 2 и получите 102. 102 делится на 34, что показывает, что 102 — общий знаменатель.
После того как вы научились находить общий знаменатель, можно переходить непосредственно к алгоритму сложения (или вычитания) общих дробей с разными знаменателями.
- Находим общий знаменатель данных дробей.
- Находим дополнительный множитель к числителю каждой дроби, разделив общий знаменатель на числитель каждой дроби.
- Умножаем каждый числитель на дополнительный множитель.
- Выполняем сложение (вычитание) дробей с одинаковыми знаменателями.
Найдите общий знаменатель. Поскольку 11 — простое число, этот метод можно использовать при умножении 11 и 14. Поэтому общий знаменатель — 154. Найдите дополнительный множитель для каждого числителя.
Выполняем сложение дробей с одинаковыми знаменателями:
Обратите внимание! Теперь у вас есть скобки! Здесь нужно быть очень осторожным. Скобки появляются потому, что перемножаются весь числитель и весь знаменатель.
Сложение и вычитание дробей
Дробь — это обычное число, которое можно складывать и вычитать. Однако, поскольку они содержат знаменатель, они требуют более сложных правил, чем целые числа.
Рассмотрим простейший случай, когда есть две дроби с одинаковым знаменателем. Итак.
Чтобы использовать тот же знаменатель, сложите числитель и оставьте знаменатель без изменений.
Если вам нужен тот же знаменатель, вычтите числитель первой дроби из числителя второй дроби и не меняйте знаменатель.
Вопрос. Найдите значения уравнений.
В каждом уравнении знаменатели дробей равны. Определяя сложение и вычитание дробей, получаем
![]()
Как видите, ничего сложного нет. Вы просто складываете или вычитаете числители, и все.
Однако даже при таких простых операциях люди умудряются совершать ошибки. В большинстве случаев они забывают, что знаменатель остается неизменным. Например, когда вы добавляете, вы прибавляете, что в корне неверно.
Избавиться от вредной привычки складывать знаменатели очень легко. Попробуйте сделать то же самое с вычитанием. Результат — ноль в знаменателе и дробь (внезапно!) теряют свое значение.
Так что помните. При сложении и вычитании знаменатель не меняется.
Многие люди также допускают ошибки при добавлении более одной отрицательной части. Существует путаница с символами: куда поместить негатив, а куда позитив.
И эту проблему очень легко решить. Помните, что минус перед символом дроби всегда можно перенести в числитель и наоборот. И, конечно, не забывайте два простых правила.
Давайте рассмотрим несколько примеров.
Вопрос. Найдите значения уравнений.
В первом случае все просто, а во втором — вычтите числитель дроби.
Что делать, если знаменатели разные
Нельзя напрямую складывать дроби с разными знаменателями. По крайней мере, я не знаю никакого способа сделать это. Однако вы всегда можете переписать исходную дробь так, чтобы знаменатели были одинаковыми.
Существует множество способов преобразования дробей. Три из них рассматриваются в курсе «Уменьшение общего знаменателя», поэтому их анализ здесь не требуется. Вместо этого давайте рассмотрим несколько примеров.
Вопрос. Найдите значения уравнений.
В первом случае используйте метод перекрестного сокращения, чтобы привести дробь к общему знаменателю. Во втором случае ищите EAP. Обратите внимание, что 6 = 2-3 и 9 = 3-3. Последний множитель этих разложений равен, а первый множитель взаимно прост. Таким образом, НОК (6; 9) = 2-3 —3 = 18.
Что делать, если у дроби есть целая часть
Позвольте вас обрадовать: разные знаменатели дробей — не самое большое зло. Еще больше ошибок возникает, когда сумма дробей имеет целые доли.
Конечно, у этих дробей есть свои алгоритмы сложения и вычитания, но они очень сложны и требуют длительного изучения. Лучшим подходом является использование простых геометрических форм, таких как
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Правила преобразования в неправильные дроби и выбора целого объясняются на уроке «Что такое арифметические дроби?». и подробно объясняются на уроке «Что такое арифметическая дробь? Обязательно повторите их, если вы их не запомнили. Пример.
Вопрос. Найдите значения уравнений.
Это самая простая часть. Поскольку знаменатели каждого уравнения равны, остается только преобразовать все дроби в неправильные дроби и измерить их. Вот:.
Для упрощения расчетов в последнем примере были пропущены некоторые очевидные шаги.
Небольшое замечание по последним двум примерам, где удалены целые дроби. Минус перед второй дробью означает, что удаляется вся дробь, а не только целое число.
Прочитайте это утверждение еще раз, посмотрите на примеры и подумайте над ними. На этом этапе начинающие совершают много ошибок. Именно по таким проблемам любят проводить викторины. Вы также неоднократно встретите их в тестах этого урока. Это будет опубликовано в ближайшее время.
Запишите сумму числителя к числителю с правой стороны и раскройте скобку числителя с правой стороны. Другими словами, перемножьте все вместе, чтобы получить одно и то же. Знаменатель не раскрывает скобку. Обычно принято оставлять произведение в знаменателе. Мы принимаем:.
Вычитание дробей. Вычитание дробей с разными знаменателями.
Следующее действие, которое может быть выполнено над нормальной фракцией, — это удаление. Дробь удаляется по разным правилам. Эти правила известны в деталях. Удаление смешанных дробей с разными знаменателями можно найти, перейдя по ссылке.
Пока рассмотрим пример, когда удаление больше, чем абстракция.
Чтобы удалить дроби с одинаковым знаменателем, необходимо удалить разность между удаляемыми числителем и знаменателем, а знаменатель оставить без изменения.
Вычитание дробей с разными знаменателями.
Чтобы удалить дроби с разными знаменателями, сложите дроби с общим знаменателем и примените правила удаления для дробей с одинаковым знаменателем.
Удаление фракций \(⌘ frac \) и \(⌘ frac \).
Общий знаменатель этих двух дробей LATEX \ FRAC/LATEX и \ frac \ frac) равен 6. Умножьте вторую дробь \ (\ frac) на один дополнительный коэффициент 3.
Сократите дробь ⌘ (⌘ frac) до ⌘ (⌘ frac).
Алфавитная система удаления дробей с разными знаменателями.
Вопрос: Как удалить дроби с разными знаменателями? ОТВЕТ: найдите общий знаменатель, а затем следуйте правилам удаления дробей с одинаковым знаменателем.
Как удалить дроби с одинаковым знаменателем? Ответ: Измерьте разность между числами и оставьте тот же знаменатель.
Как проверить удаление двух дробей? Ans: Чтобы проверить удаление дробей, сложите сумму и разность, действие их суммы равно абстракции.
Пример №1: Выполнение дробного удаления: a) \(\ frac- \ frac) b) \(\ frac- \ frac)
Удаление двух одинаковых фракций приводит к нулю.
Пример 2: Выполнение контроля удаления и добавления: a) \(\ frac- \ frac)b)\(\ frac- \ frac) Раствор.
(a) Найдите общий знаменатель дробей \(⌘ frac) и \(⌘ frac): 21. Умножьте вторую дробь \(⌘ frac) на 3. (b) Найдите общий знаменатель дробей \(⌘ frac) и \(⌘ frac): 21.
Проверьте удаление.
(b) Найдите общий знаменатель дробей \frac и \frac. 15. Умножьте первую дробь ⌘ (⌘ frac) на дополнительный коэффициент 5 и вторую дробь ⌘ (⌘ frac ⌘ frac ⌘ frac ⌘ frac. ) на 3.
Проверьте удаление.
You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.
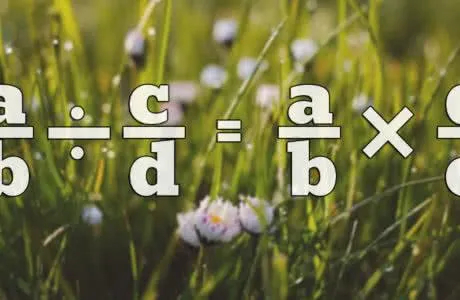
Деление дробей. Правила. Примеры.
Добавить комментарий Отменить ответ.
Вы должны войти в систему, чтобы написать комментарий.
Свежие записи
Если вы хотите продолжить работу над проектом, отключите блокировку рекламы или добавьте сайт в исключение.
Все дроби в этом ряду правильные, и числитель меньше знаменателя. Исключите один. Да, да, вы правы, например, числитель может быть больше знаменателя, как в этой дроби: \(\ displaystyle 17/3 \).
Вычитание дробей с разными знаменателями.
Или, в противном случае, удалите различные фракции.
Правила вычитания дробей с разными знаменателями. Чтобы вычесть дроби с разными знаменателями, их нужно сначала привести к наименьшему общему знаменателю (НОЗ), а затем вычесть как дроби с одинаковым знаменателем.
Наименьший общий знаменатель многих дробей — это наименьшее общее кратное натурального числа, которое является знаменателем дроби.
Внимание! Если в конечной дроби числитель и знаменатель имеют общие элементы, то дробь необходимо сократить. Неправильные дроби должны быть представлены в виде смешанных дробей. Там, где возможно, оставить эффект вычитания без уменьшения дроби — это несовершенное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители; все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Сложение и вычитание дробей, содержащих буквы в числителе, выполняется аналогичным образом.
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) целое вычитается из целого, а часть вычитается из части.
Первый вариант вычитания смешанных дробей.
Если знаменатели дробных частей одинаковы, а числитель (источник вычитания) дробной части вычитаемого больше или равен числителю (источнику вычитания) дробной части вычитаемого.
Второй метод удаления смешанных фракций.
Если знаменатели дробной части разные. Сначала приведите дробную часть к наименьшему общему знаменателю, затем вычтите дробную часть из десятичной, затем вычтите десятичную часть из дробной.
Третий вариант вычитания смешанных дробей.
Дробная часть делителя меньше дробной части делимого.
Дробная часть имеет другой знаменатель и поэтому добавляет к дроби общий знаменатель.
Числитель дроби минус меньше числителя дроби вычитания. 3< 14. Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
Сложите полученную неправильную дробь 18/18 и дробь вычитания, чтобы получить
В результате получается общая схема расчета.
- Если есть целая часть, переводиме эти дроби в неправильные;
- Приводим все дроби к общему знаменателю любым способом;
- Вычитаем найденные числа по правилу вычитания дробей с одинаковыми знаменателями;
- Если есть возможность, сокращаем полученную дробь. Если дробь получилась неправильной, выделяем целую часть.
- Запомните, что выделяем целую часть предпочтительно в конце выполнения задания, именно перед записью ответа. Так легче не запутаться.
Просто умножьте знаменатель. Обычно этот метод используется, когда дано первое число (делится на 1 и само на себя) и не может быть разложено на множители.
Вычитание дробей
При удалении и добавлении фракций могут возникать различные случаи.
При вычитании дробей с одинаковым знаменателем числитель вычитаемой дроби (первая дробь) к числителю вычитаемой дроби (вторая дробь) остается знаменателем.
Помните!
Прежде чем написать окончательный ответ, проверьте, можно ли сократить получившиеся дроби.
Правило вычитания дробей с одинаковым знаменателем записывается следующим образом
Вычитание правильной дроби из целого числа
Чтобы вычесть правильную дробь из целого числа, это натуральное число должно быть выражено как смешанное число.
Для этого возьмите единицу натурального числа и представьте ее в виде неправильной дроби. Его знаменатель совпадает со знаменателем вычитаемой дроби.
7 7и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание смешанных чисел
При вычитании смешанных чисел дробная часть вычитается отдельно от десятичной части, а дробная часть вычитается из дробной части.
При таких расчетах могут возникать различные случаи.
Первый случай вычитания смешанных чисел
Дробная часть имеет одинаковый знаменатель, а числитель дробной части вычитаемого (из которой вычитается) больше или равен числителю дробной части вычитаемого (из которой вычитается).
Второй случай вычитания смешанных чисел
Десятичная часть имеет другой знаменатель.
В этом случае сначала сократите дробную часть до наименьшего общего знаменателя, затем вычтите целое из дробной части, а затем вычтите дробную часть из дробной части.
Третий случай вычитания смешанных чисел
Дробная часть делителя меньше дробной части делимого.
Если знаменатели дробных частей разные, как во втором случае, сначала сократите дробь до общего знаменателя.
Числитель дробной части вычитаемого меньше числителя дробной части вычитаемого.
Поэтому, не забыв вычесть обычную дробь из целого числа, возьмите единицу из части целого числа и представьте эту единицу в виде неправильной дроби с тем же знаменателем и числителем, равным 18.
Сложим полученную неправильную дробь
| 18 |
| 18 |
и дробную часть уменьшаемого и получим:
Все рассматриваемые случаи можно объяснить, применив правило вычитания смешанных чисел.








