-прямоугольный тетраэдр. Каждое ребро, касательное к вершине, перпендикулярно другим ребрам, касательным к той же вершине.
Тетраэдр
Тетраэдр (греч. tetrahedron) — простейший многогранник, гранями которого являются четыре треугольника. Тетраэдр имеет четыре грани, четыре вершины и шесть ребер.
- Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
- Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
- Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Свойства тетраэдра
Существуют следующие специальные типы тетраэдров
-
, у которого все грани — равные между собой треугольники., у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.
- Прямоугольный тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой., у которого все грани — равносторонние треугольники. — тетраэдр, отвечающий любому из следующих условий: 2
- существует сфера, касающаяся всех ребер,
- суммы длин скрещивающихся ребер равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, вписанные в грани, попарно касаются,
- все четырехугольники, получающиеся на развертке тетраэдра, — описанные,
- перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
Объём тетраэдра
Тетраэдр, вершины которого находятся в точках (с учетом знака), объем которого равен
Равный 、、、、、、
«ширина =» «» высота =» «» />
-
, Лёд, Н2О
- Молекула метана СН4
- Молекула аммиака NH3 Тетраэдры с гранями С, равными 2,5220 ангстрем CaF2, тетраэдр с ребром равным 3, 8626 ангстрем, ZnS, тетраэдр с ребром равным 3,823 ангстрем
- Комплексные ионы BF4 -, ZnCl4 2-, Hg(CN)4 2-, Zn(NH3)4 2+, структура которого основана на тетраэдре SiO4 4-
В начале курса «Стереометрия» было сказано, что все геометрические объекты можно разделить на объекты вращения и полиэдры. Мы подробно обсудим свойства этих и других фигур при изучении геометрии в 10 классе.
Тетраэдр.
Тетраэдр является частным случаем правильной треугольной пирамиды.
Тетраэдр — это правильный многогранник (четырехугольник) с четырьмя гранями; правильный многогранник — это правильный треугольник. Тетраэдр имеет четыре вершины и три ребра, сходящиеся к каждой вершине. Общее количество граней в тетраэдре равно шести.
Средняя линия тетраэдра — это пересечение вершины тетраэдра и противоположной средней линии (средней линии равностороннего треугольника напротив вершины).
Диполь тетраэдра — это часть, соединяющая середины пересекающихся ребер (соединяющая середины сторон треугольника, который является одной из граней тетраэдра).
Высота тетраэдра — это часть, соединяющая точки, противоположные вершине и перпендикулярные этой стороне (то есть высота, проведенная из каждой стороны, за исключением той, которая совпадает с центром окружности). .
Свойства тетраэдра.
Параллельные плоскости, проходящие через пересекающиеся пары граней тетраэдра, определяют параллелограмм, очерченный вокруг тетраэдра.
Плоскость, проходящая через середину двух пересекающихся граней четырехгранника и делящая его на две части равного объема.
Все средние линии и делители тетраэдра пересекаются в одной точке. Эта точка делит среднее значение сверху на 3:1. Он также делит двустороннюю часть на две равные части.
Типы тетраэдров.
Тетраэдр — это такая пирамида из правильных треугольников, что каждая сторона является равносторонним треугольником.
В правильном тетраэдре угол между каждой биссектрисой ребра и каждым треугольником вершины имеет одинаковую величину.
Тетраэдр состоит из четырех граней, четырех вершин и шести ребер.
Тетраэдр — это один из пяти правильных многогранников.
Помимо обычных тетраэдров, внимания требуют следующие типы тетраэдров.
-Правильный тетраэдр, в котором каждая сторона является треугольником. Поверхности всех треугольников такого тетраэдра равны.
-Тетраэдры с ортоцентрами. Каждая высота спускается от вершины к противоположной стороне и пересекает другие вершины в одной точке.
-прямоугольный тетраэдр. Каждое ребро, касательное к вершине, перпендикулярно другим ребрам, касательным к той же вершине.
Каркасный тетраэдр — это тетраэдр со следующими условиями.
- есть сфера, которая касается каждого ребра,
- суммы длин ребер, что скрещиваются равны,
- суммы двугранных углов при противоположных ребрах равны,, которые вписаны в грани, попарно касаются,
- каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.
-Это общий тетраэдр, и обе его высоты одинаковы.
Эксцентрический тетраэдр с соединительной частью, соединяющей вершины тетраэдра и центр окружности, вписанной в противоположную сторону, пересекается в точке.
Тетраэдр — это правильный многогранник (четырехугольник) с четырьмя гранями; правильный многогранник — это правильный треугольник. Тетраэдр имеет четыре вершины и три ребра, сходящиеся к каждой вершине. Общее количество граней в тетраэдре равно шести.
Вариант развертки
Вы можете сделать свои собственные тетраэдры. Лучше всего подходит бумага или картон. Для сборки требуется цельная деталь с линиями складывания.
Древнегреческий философ Платон связывал тетраэдр с элементом «земли» — огнем, поэтому он решил создать модель этого многогранника, обычно окрашенного в красный цвет.
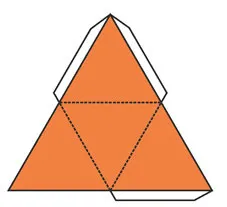
Обратите внимание, что это не единственный вариант развертывания.
Чтобы построить модель, скан можно загрузить в формате PDF и распечатать на листе формата A4. -Для печати на цветном принтере -Цветное сканирование -Для использования цветного картона -Сканирование.
Видео. Тетраэдр из набора «Волшебные грани»


Вы можете использовать Magic Face Set Assembly для создания четырехсторонней модели.
Сборка всего Хедрала:.
Подробная сборка от Алексея Жигулева (YouTube Pro Channel)
Подробная сборка от Алексея Жигулева (YouTube Pro Channel)
Вращающиеся готовые многогранники:.
(2) Характерным свойством четырехслойного слоя является то, что рисунок встречает интерстиций и океан в один и тот же момент времени. Важно, чтобы последний разделял носители в соотношении 3:1 и центральное место.
Виды тетраэдра
Разнообразие видов форм очень велико. Тетраэдры выглядят следующим образом.
- правильным, то есть в основании равносторонний треугольник;
- равногранным, у которого все грани одинаковы по длине;
- ортоцентрическим, когда высоты имеют общую точку пересечения;
- прямоугольным, если плоские углы при вершине нормальные;
- соразмерным, все би высоты равны;
- каркасным, если присутствует сфера, которая касается ребер;
- инцентрическим, то есть отрезки, опущенные из вершины в центр вписанной окружности противоположной грани, имеют общую точку пересечения; эту точку именуют центром тяжести тетраэдра.
Подробно остановитесь на правильном тетраэдре. Его характеристики практически не отличаются.
Его так называют потому, что его лицо обычно имеет треугольную форму. Все края этой фигуры соответствуют ее длине, а поверхность повторяет площадь. Обычный тетраэдр — это один из пяти одинаковых многогранников.
Формулы четырехгранника
Высота тетраэдра равна длине 2/3 корня и ребра.
Объем тетраэдра рассматривается так же, как и объем пирамиды: разделите 12 на квадратный корень из 2 и умножьте на длину куба.
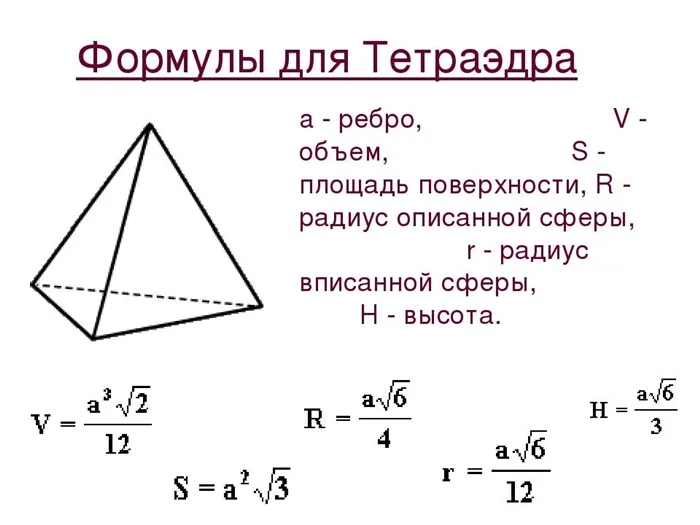
Другие типы для вычисления площади и лучей круга показаны выше.
(b) По условию необходимо найти площадь прямоугольника, составленного из векторов. Площадь этого прямоугольника численно равна длине векторного произведения. Площадь этого прямоугольника численно равна длине векторного произведения.
Большой тетраэдр из картона
Картонный тетраэдр (который можно сделать по инструкции, приведенной ниже в статье) прочный и хорошо держит форму. Размер трехмерной фигуры зависит от типа гофрокартона.
Какой тип гофрированного картона можно использовать для работы:.
- Цветной (для детского творчества). Подойдет для создания тетраэдров высотой до 25 см. Этот картон довольно тонкий, поэтому крупная фигура, сделанная из него, будет неустойчивой. Грани могут прогнуться и деформироваться. Зато из цветного картона можно сделать разноцветный тетраэдр, если использовать для каждой грани лист другого цвета. В таком случае развёртка будет отличаться от стандартного варианта. Все грани потребуется начертить отдельно и добавить к ним «ушки» для крепления.
- Полиграфический. Этот картон более плотный. Его используют для создания твердого переплета книг и блокнотов, а также для упаковки мелкого товара. Из такого картона можно собрать тетраэдр высотой от 25 до 45 см.
- Упаковочный. Самый прочный тип картона. Он имеет гофрированную текстуру и состоит из нескольких слоев. Работать с таким материалом сложно, но из него получаются крепкие фигуры. Размер тетраэдров может быть более 45 см в высоту. Такие фигуры можно использовать для домашнего декора.

После сборки тетраэдров нецветной гофрокартон можно покрасить или покрыть узором. Необычные украшения для рабочего стола можно получить, приклеив по краям маленьких фигурок листки календаря или фотографии.
Особенности работы с жестким картоном
Четырехугольник из гофрированного картона (который можно разрабатывать поэтапно без использования стандартов) выполняется по следующим правилам
- Для построения чертежа удобнее использовать длинную линейку (около 30 см). Составляя развёртку с короткой линейкой можно легко ошибиться. Из развёртки с погрешностями очень сложно собрать ровную фигуру.
- Вырезать заготовку нужно канцелярским ножом, прикладывая к линиям линейку. Использовать ножницы можно только для тонкого картона. На плотном материале не получится ровных срезов. В некоторых местах будут образовываться заломы.
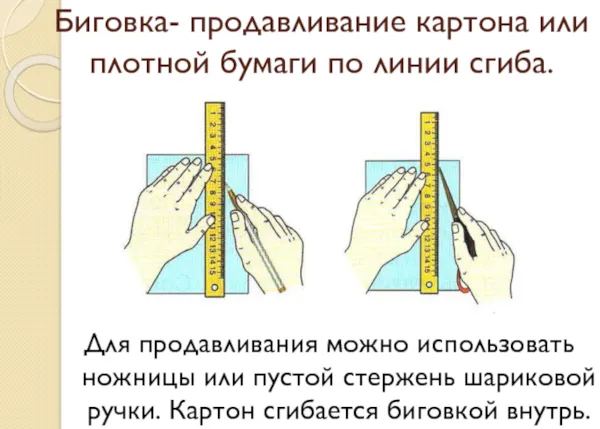
- Чтобы согнуть упаковочный картон, его нужно продавить. Для этой цели не желательно использовать линейку или стержень от ручки. Эти инструменты могут повредить несколько слоев картона, а при сильном давлении, вовсе порвать его. Лучше воспользоваться тупым концом ручки или десертной ложки. Тогда линии получаться толще, но картон не порвётся.
- Когда деталь будет вырезана, необходимо осмотреть её со всех сторон и срезать мелкие заусенцы.
- Фиксировать «ушки» для склеивания нужно по очереди. Прежде, чем смазать клеем новое «ушко», нужно дождаться полного высыхания клея на предыдущем.
Удобнее работать с двумя слоями гофрированного картона. Его можно вырезать из более крупных коробок, в которые переносятся приборы. С гофрированным картоном с тремя и более слоями работать гораздо сложнее. Такие материалы трудно согнуть и приклеить.
Тетраэдр (от Tetra и греч. Hedra — грань), один из пяти типов правильных многогранников, правильная треугольная пирамида. Четыре треугольные поверхности, шесть ребер, четыре вершины и три ребра сходятся на каждой … Современная энциклопедия.
Тетраэдр
В начале урока по стереометрии мы говорили, что все геометрические тела делятся на тела вращения и многогранники. Изучая геометрию в 10 классе, мы рассматриваем свойства конкретных фигур. В этой видеоцитате мы знакомимся с такими фигурами, как тетраэдры. Мы ознакомимся с основами тетраэдров. Мы решим некоторые проблемы, связанные с этим вопросом.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к другим видеосеминарам из комплекта, необходимо приобрести их из списка и добавить в личный кабинет.

Конспект урока «Тетраэдр»
В начале курса «Стереометрия» было сказано, что все геометрические объекты можно разделить на объекты вращения и полиэдры. Мы подробно обсудим свойства этих и других фигур при изучении геометрии в 10 классе.
Сегодня вы познакомитесь с такими фигурами, как тетраэдр. Прежде чем приступить к изучению пространственной геометрии, давайте вернемся к планетам и вспомним такие многоугольники.
Помните, что многоугольник — это либо замкнутая линия без независимого разреза, либо часть уровня, определяемая этой линией, включая саму линию.
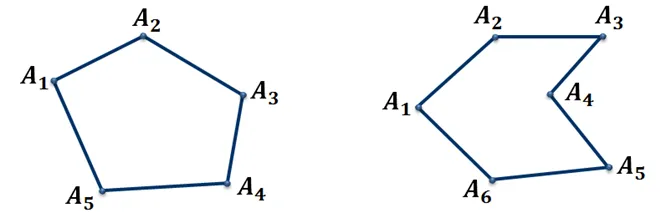
Что касается определений, то второе определение подходит более естественно. Это определение утверждает, что все многоугольники являются плоскими поверхностями.
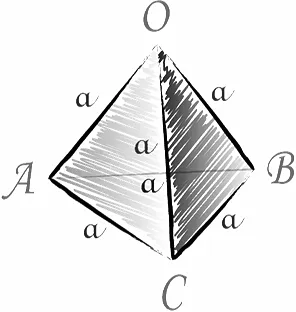
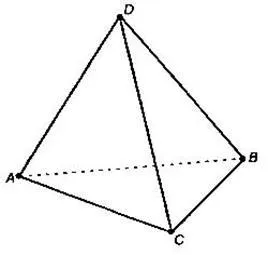
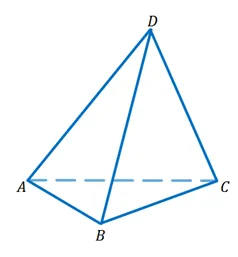
Помните, что самый простой многоугольник — это треугольник. Получите треугольник ABC из треугольника ABC и точки D. Это не на уровне треугольника ABC. Соедините точку D с вершиной каждого треугольника ABC. Таким образом, вы получаете три новых треугольника DAB, DBC и DCA. Фигура, состоящая из четырех треугольников ABC, DAB, DBC и DCA, называется тетраэдром и обозначается DABC.
Треугольники, из которых составлен тетраэдр, называются гранями, стороны этих треугольников — ребрами, а вершины этих треугольников — вершинами тетраэдра.
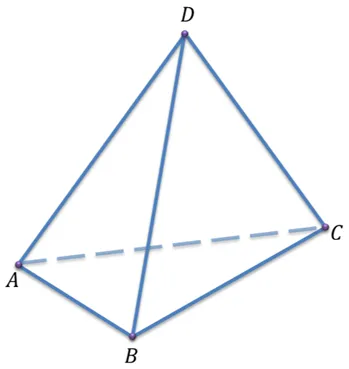
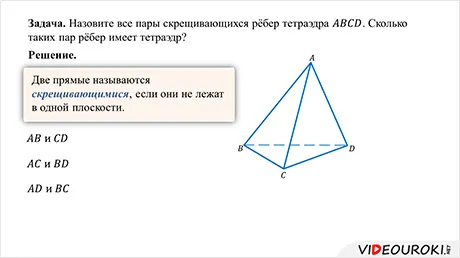
Нетрудно подсчитать, что тетраэдр имеет четыре грани, шесть ребер и четыре вершины. Два ребра четырехугольника, которые не имеют общих вершин, называются противоположными. Запишите пары рядом с гранями четырехугольника, изображенного на рисунке.
Эти ребра — AD и BC, BD, AC, CD и AB. Иногда одну из четырехгранных граней называют основанием, а остальные три — сторонами.
Слово тетраэдр происходит от древнегреческого tetr, что означает четыре, и edra, что означает основание или внешний вид.
Если все грани тетраэдра являются равными треугольниками, то такой тетраэдр называется нормальным тетраэдром. Нормальные тетраэдры являются одним из пяти нормальных многогранников. Их также называют платоновыми твердыми телами. Это тетраэдр, гранью которого являются четыре прямоугольных треугольника, куб с шестью квадратами, октаэдр с восемью треугольными гранями, тетраэдр, гранью которого являются 12 прямоугольных пятиугольников и 203 33 грани с 12 гранями.
Поклонники пифагорейской философской школы придавали форму четырех стихий четырем годам огня.
Тетраэдр, у которого все грани представляют собой равные треугольники, называется правильным женским тетраэдром.
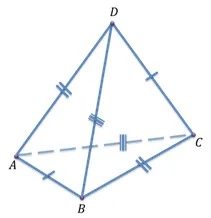
Если ребра верхних соседних четырехугольников перпендикулярны друг другу, то такой тетраэдр называется прямоугольным тетраэдром.
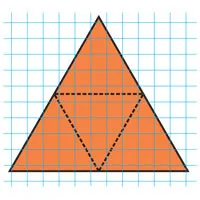
Тетраэдры обычно рисуются в виде выпуклых квадратов или неизогнутых квадратов с диагоналями. Пунктирные линии обозначают невидимые края.
В этой форме невидимыми остаются только прыщи переменного тока.
(2) Характерным свойством четырехслойного слоя является встреча интерстициального и океанического морей в один и тот же момент времени. Важно отметить, что в последнем случае СМИ делятся в соотношении 3:1 и в центральном приморском соотношении.
Формулы объема тетраэдра
Конкретные количества тела можно найти разными способами. Давайте обсудим некоторые детали.
Через смешанное произведение векторов
Если тетраэдр составлен из трех векторов с координатами: .
Тогда объем этого тетраэдра является смешанным произведением этих векторов, т.е. спецификатором.
Объем четырех -оф -грейд через определение
Координаты четырех вершин октавы известны.
D (7, 1 2, 1). Найдите его объем.
Первым шагом является определение координат вектора, по которому это тело структурировано. Для этого найдите каждую координату вектора, удалив соответствующие две координаты точки. Например, координаты вектора
a b, т.е. вектор, направленный через точку
b, — разность между соответствующими координатами точек
a b = (8-1, 7-4, 3-9) = (7, 3, -6)
c = (1-1, 2-4, 3-9) = (0, -2, — 6)
a d = (7-1, 1 2-4, 1-9) = (6, -8, -8)
Теперь давайте найдем смешанное произведение этих векторов, построив спецификатор третьего класса.
Формула объема равногранного тетраэдра по его стороне
Этот тип применяется только для вычисления объема равносторонних треугольных четырехугольников. То есть четырехугольник, все поверхности которого состоят из равных прямоугольных треугольников.
Опухоль.
Определите объем четырехугольника, если даны его стороны
Для четырехстороннего объема введите:.
v = 1 22⋅a3 = 1 2 2⋅13≈15 6. 8 см 3
Виды тетраэдра
Разнообразие видов форм очень велико. Тетраэдры выглядят следующим образом.
- правильным, то есть в основании равносторонний треугольник;
- равногранным, у которого все грани одинаковы по длине;
- ортоцентрическим, когда высоты имеют общую точку пересечения;
- прямоугольным, если плоские углы при вершине нормальные;
- соразмерным, все би высоты равны;
- каркасным, если присутствует сфера, которая касается ребер;
- инцентрическим, то есть отрезки, опущенные из вершины в центр вписанной окружности противоположной грани, имеют общую точку пересечения; эту точку именуют центром тяжести тетраэдра.
Подробно остановитесь на правильном тетраэдре. Его характеристики практически не отличаются.
Из названия ясно, что он называется так потому, что его стороны являются нормальными треугольниками. Все края этой фигуры соответствуют длине, а поверхность повторяет площадь. Обычный тетраэдр является одним из пяти подобных многогранников.
Тетраэдры в технике
- Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм мостов и т. д. Стержни испытывают только продольные нагрузки.
- Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов .
- Граф четверичного триггера представляет собой тетраэдр.
Площадь прыща в четырехугольнике задачи 1 равна 24 см2, а высота прыща — 9 см. Найдите объем фигуры.
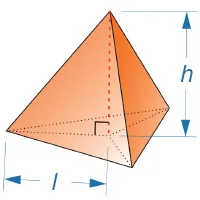
Решение: примените общую формулу для получения.
В задаче 2 дан обычный тетраэдр, пупырышек которого равен 8 см. Найдите его объем.
Решение: вычислите объем нормальной фигуры, используя тип.








