Чтобы убрать ненужное умножение на степени, вид y = a2 -x² + a1 -x + a0 преобразуется в y = ((0 + a2)-x + a1)-x + a0.
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Тригонометрия — это раздел математики, изучающий тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще в Древней Греции. В Средние века ученые Ближнего Востока и Индии внесли важный вклад в развитие этой науки.
В этой статье рассматриваются основные понятия и определения тригонометрии. Объясняются основные тригонометрические определения, синус, косинус, тангенс и цыпленок. Объясняется и изображается их значение в геометрии.
Синус, косинус, тангенс и котангенс. Определения
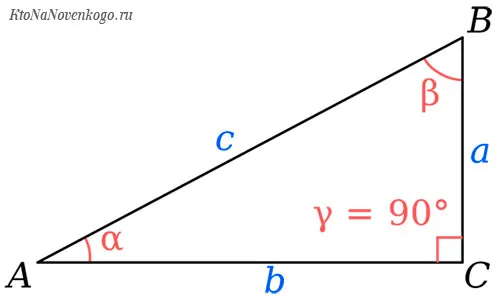
Определение тригонометрических функций, где аргументом является угол, сначала выражается через основания сторон прямоугольного треугольника.
Определение тригонометрических функций
Полутон угла (sin a) является основанием противоположного угла гипотенузы.
Косинус угла (cos a) является причиной подчиненности смежной вертикали.
Тангенс угла (t g a) — отношение смежных противоположных катетов.
Угловой угол (c t g a) — это отношение соседних противоположных катетов.
Эти определения даны для острых углов прямоугольного треугольника!
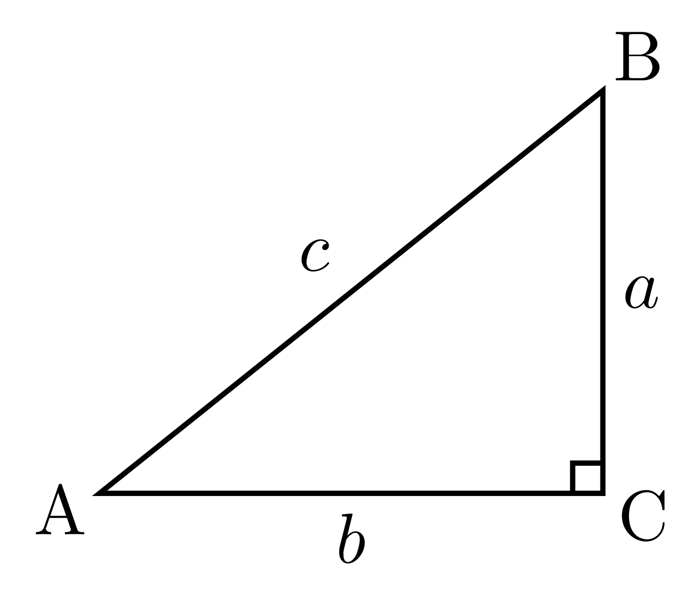
В треугольнике ABC с прямым углом C половина угла A равна причине перпендикуляра BC меньшего AB.
Определения синуса, косоугольника, тангенса и котангенса позволяют вычислить значения этих функций по известным длинам сторон треугольника.
Ширина синуса и космитонуса варьируется от -1 до 1. Другими словами, синус и косинус возрастают от -1 до 1. Диапазоны тангенсов и котениоид являются целочисленными линиями. Произвольные цены.
Угол поворота
Приведенное выше определение относится к острым углам. Тригонометрия знакомит со значением угла поворота. Его значение не ограничено рамками 0-90 градусов, в отличие от острого угла.
В этом контексте можно определить синус, косинус, тангенс и произвольный угловой цыпленок. Представьте себе единичную окружность с центром в начале декартовой системы координат.
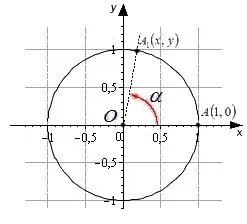
Исходная точка A с координатами (1, 0) поворачивает центр единичной окружности на угол A, переходя из точки 1 в точку 1. Определение дано координатами точки a 1 (x, y).
Синус угла A является прямым углом точки a 1 (x, y). sinα= y
Косинус угла поворота A — это дивергенция точки a 1 (x, y). cosα= x
Касательная к углу поворота A — это отношение к дальнему концу порядка точек a 1 (x, y). Tgα= y x
Прибрежный угол поворота a является причиной конечного угла размещенной точки a 1 (x, y). C TGα= x y
Синус и косинус определяются для любого угла поворота. Это разумно, так как дальний и ближний углы точки после вращения могут быть определены под любым углом. Это не относится к тангенсам и косинусам. Касательные не могут быть определены, если точка после вращения переходит в нулевое положение (0, 1) и (0, -1). В таких случаях представление касательной линии tgα= y x просто бессмысленно, так как содержит нулевое деление. Ситуация с курицей аналогична. Разница заключается в том, что тренер не может быть определен, если манускрипт очков сброшен.
Синус и косинус определены для любого угла a.
Касательные определены для всех углов, кроме a = 90° + 180°-k, k ∈ Z (α = π2 +π -k, k ∈ Z).
Пилигрим определяется для всех углов, кроме a = 180°-k, k ∈ Z (α = π -k, k ∈ Z).
При решении практических примеров не говорят «половина угла поворота». Термин «угол поворота» просто сокращен, то есть из контекста понятно, о чем идет речь.
При решении практических примеров не говорят «половина угла поворота». Термин «угол поворота» просто сокращен, то есть из контекста понятно, о чем идет речь.
Синус числа
Синус числа можно определить с помощью числовой окружности – синус числа равен ординате соответствующей точки на ней.
Обычно для обозначения любого количества знаков используется ряд цифр, но найти знак числа, связанный каким-либо образомПи. : \frac \frac \frac \frac}, \frac}, \frac} (-2p).
Например, для \ (\ frac \) знак будет \ (0,5 \). В случае числа, 섹(- \)섹(섹 frac) — это 섹(- \)섹(섹 frac> \) (для 섹(-0,71 \)).
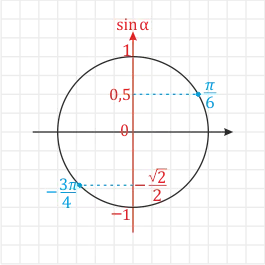
Вы можете прочитать больше о том, как рассчитать количество половинок для различных чиселЭта статья. .
Значение синуса всегда лежит в пределах от \(-1\) до \(1\). При этом вычислен он может быть для абсолютно любого угла и числа.
Синус любого угла
Используя единичный цикл, можно определять тригонометрические функции не только для острых углов, но и для тупых, отрицательных и даже свыше ⌘ (360° ⌘) (полный цикл). Как это сделать — проще один раз увидеть, чем один раз услышать, см. рисунок.
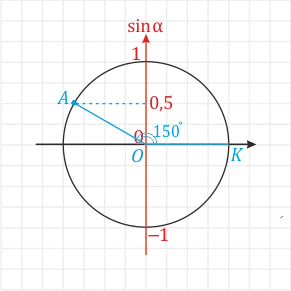
Пояснение здесь: определим ⌘ (sin Ј) на шкале оценки ⌘ (150 ° Ј). Совместите точки центра и стороны OK окружности на оси ⌘(x \). Затем отсчитайте \(150°\) против часовой стрелки. Далее вы увидите Ј(Јsin∠koa\) в строке A.
Если вас интересуют градусные углы, например ⌘(-60°⌘) (угол ков), сделайте то же самое, но ⌘(60°⌘) отложите по часовой стрелке.
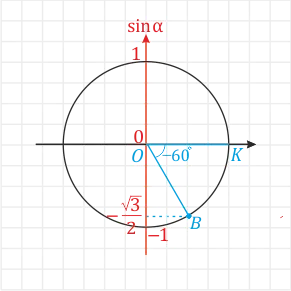
И, наконец, углы больше Lu_40°F(-360°\) (угол kos) — все тускнеет и полный поворот происходит только вправо, а затем переходите ко второму циклу и «добирайте недостающий градус». В этом случае угол ⌘ (405°\) дается как ⌘ (360° + 45°\).
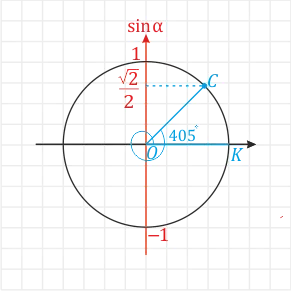
Например, легко догадаться, что для угла \(960°\) требуется два вращения (\(360° + 360° + 240°\)), а для угла \(2640°\) — и семь.
Как вы уже догадались, синус половины числа и любого угла примерно одинаков. Меняется только метод нахождения точки окружности.
Связь с другими тригонометрическими функциями:
-. Косинус. Тот же угол (или то же число): базовая тригонометрия ID \(⌘ sin^2x+⌘ cos^2x = 1 \) — и Тангента. и косинус одного и того же угла (или числа): тип \(tgx = \) \(\ frac) — с со своей курицей. тот же угол (или число): см. другие более частые типы по формуле ⌘ (1+ctg^2x = \) ⌘ (⌘ frac)Вот. .
Построив значения синусов, соответствующих углам радиуса на оси x, и эти углы на оси y, получим следующий график
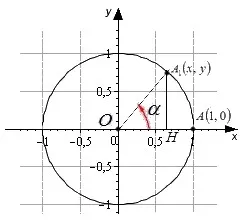
График этогоФункции. Он называется синусоидальной волной и обладает следующими свойствами:.
— Областью определения является любое значение x:ዄ(d(ዄ sinx) = r \) — диапазон цен от ዄ(-1 \) до ዄ(1 \). \（e（\ sinx）= — 1; 1 \) не требуется: \（\ sin（-x）= — \ sinx \) — Период \(2p): \（\ sin（x+2p）= \ sinx \) — Использование координатных осей пересечения: ось абсцисс: \((πn; 0)\) где \(nϵz) ось линий. ϵz) — интервал известной устойчивости: ϵ(0; 0)ϵz) — интервал известной устойчивости. Интервалы: \((2pn; π+2m)\), функция \(nϵz \) отрицательны в интервалах. ) Это последовательные и затухающие пространства: функция представляет собой возрастающий интервал \((- \)\()\(+2m)\()\(+2pn)\), где \(n ϵ z \) функция сводится к интервалу: \()\(+2m)\()\(+2pn)\ (frac) \(+2m) \), \(n ϵ z \) — это максимум и минимум Функция: функция имеет максимальное значение \(y = 1 \) в точке \(x = \) (\ frac) \(+2m), \(nϵ z \) или минимальное значение \(y = -1 \) в функции \(x = -2 \)ᢙ(ᢙ frac \)ᢙ(+2pn \), где \(nϵz \)
По этой причине наибольшее внимание уделяется базовой треугольной идентичности. Но что могут сделать «измерения» без доказательств? Если показана личность, не стесняйтесь доказывать ее.
Свойства синуса
Основные свойства знака типа перечислены в таблице ниже.
| Свойство | Формула | |||
| Симметричность | Симметричность | Пифагорейская тригонометрическая идентичность | ‘Data-Order =’ |
|
| Синус двойного угла | Синус суммы углов | Синус разности углов | Сумма синусов |  |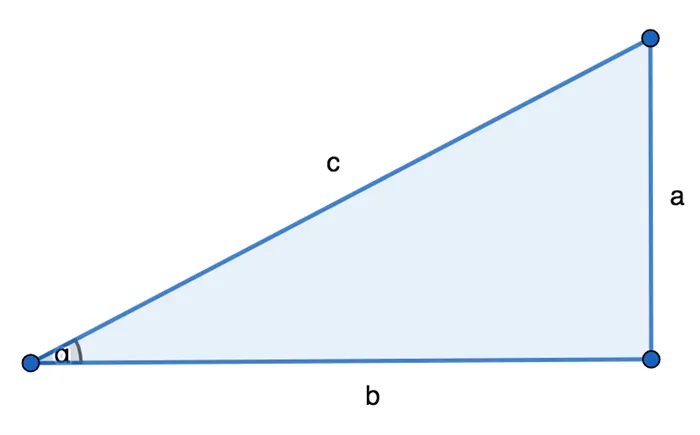
| Разность синусов |  |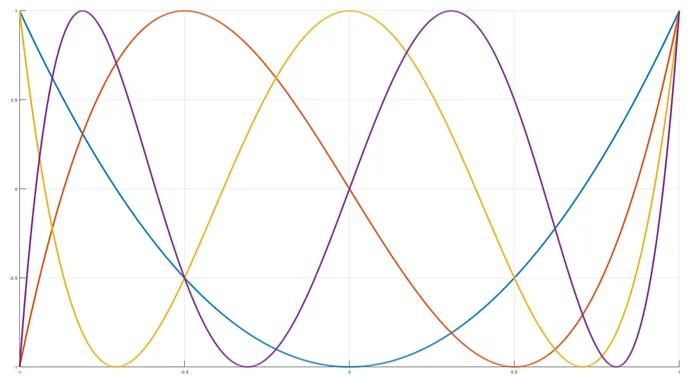
|||
| Произведение синусов |  |
|||
| Произведение синуса и косинуса |  |
|||
| Закон синуса | Производная синуса | Интеграл синуса | Формула Эйлера | Примеры решения задач
Рассмотрите некоторые проблемы, которые необходимо знать о базовых тождествах. Потренируйтесь самостоятельно, используя приведенные решения. Задачка 1. Найдите cos a, tg a, ctg a sinα= 12/13.
Задачка 2. Найдите значение cos α, если:
Замените значение sin:. Как видите, если правильно применять основные типы идентичности, проблему очень легко решить.
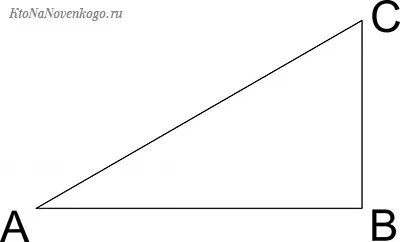
Что такое тригонометрияНо давайте начнем с основ. Сказав, что синагоги — это тригонометрические функции, позвольте мне объяснить, что такое тригонометрия. Тригонометрия — это отрасль математики, возникшая в Древней Греции. Само слово состоит из двух половинок «triangle» и «mere», что дословно можно перевести как «изучение треугольников». Нечто похожее на тригонометрические функции впервые появилось в Древней Греции. Во всяком случае, они встречаются в работах Евклида и Архимеда, то есть в третьем веке до нашей эры. Хотя ученые не исключают, что подобные расчеты использовались и при строительстве египетских пирамид. А это уже 2-2,5 тысячелетия до нашей эры. Опять же, пирамиды имеют треугольную форму (в плане). А тригонометрия напрямую связана с треугольниками. Это может совпадать, а может и не совпадать. Действительно, тригонометрия рассматривает определенные треугольники (прямоугольники). Напомним, что это фигуры, у которых две из трех сторон пересекаются под углом 90 градусов. Такой треугольник будет выглядеть следующим образом
Стороны такого треугольника имеют конкретные названия. ВЕРТИКАЛЬ — это ребро, пересекающееся под прямым углом. HYPOTHENUS — сторона, образующая угол и соединяющая два катетера. Синус — это .И теперь мы подходим к самому главному — определению SYNOUS. Это размер, который не существует сам по себе. Это связано с определенным углом треугольника. В частности, углы альфа (alpha) и бета (beta), которые наглядно показаны на следующей диаграмме.
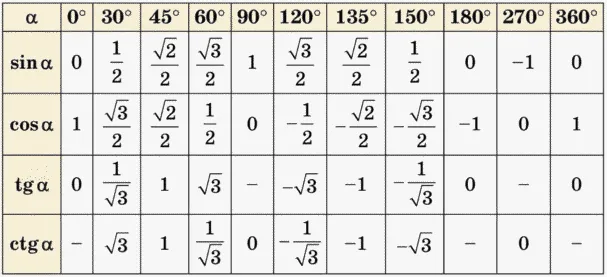
И вот долгожданное определение:. ЧИСЛО угла — это отношение перпендикулярной линии к наклонной линии. Чтобы прояснить, о чем идет речь, снова посмотрите на диаграмму прямоугольного треугольника. В этом случае профилем, противоположным углу α, является сторона BC. А противоположная сторона угла b — сторона AC. Соответственно, ножка BC угла α является смежной. И ножка BC угла b будет точно такой же. Конкретные виды знаков: a. Ножка BC угла b прилегает к ножке BC угла b. Значения синусовВ большинстве случаев студентам необходимо будет рассмотреть конкретные ракурсы. Например, 30, 45, 60 или 90 градусов. Кроме того, уже предусмотрены таблицы, чтобы ученикам не приходилось вычислять тригонометрические величины по сторонам треугольника.
 Как извлечь корень из дроби - Примеры. Приклади Получите
 Стереометрия это часть геометрии которая изучает -
 Две прямые называются перпендикулярными если - Признак
 Что такое арифметический квадратный корень - Извлечение
 Прямоугольная система координат в пространстве - Описание
 Жан лерон д аламбер - Примечания править Стремление
 Множество это в математике - Счетные и несчетные множества
|
