Действительно, соотношение выполняется, то есть отрезок в три раза короче отрезка. Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
Как находить середину отрезка
Прежде чем перейти к настоящему вопросу, я хотел бы немного поговорить о прямых отрезках, но не как о математическом определении. Многие ученые пытались по-разному взглянуть на прямые участки и пытались увидеть аномалии. Некоторые талантливые художники позволяют геометрическим формам передавать настроение и эмоции.
Существует множество теорий о том, как и почему цвета влияют на наше настроение.
Цвет имеет большое значение и тесно связан с нашими эмоциями. Цвета природы, архитектуры, растений и одежды. Они влияют на наше настроение.
Эксперты говорят, что цвета могут влиять на настроение людей.
- Красный цвет может поднять настроение, придать сил.
- Розовый цвет символизируют мир и покой.
- Оранжевый — это теплый, беспокойный цвет, дающий энергию и поднимающий настроение.
- В императорском Китае желтый считался настолько священным цветом, что носить желтую одежду мог только император. Египтяне и майя считали желтый цветом Солнца и почитали его силу, поддерживающую жизнь. Желтые цветы могут взбодрить и порадовать, когда вы чувствуете себя неважно.
- Зеленый — целительный цвет. Вызывает ощущение равновесия и гармонии.
- Синий усиливает творческое начало.
- Фиолетовый — цвет задумчивости, духовности и покоя. Он связан с интуицией и заботой о других.
- Белый обычно считается цветом чистоты и невинности. Он также связан с вдохновением, озарением, духовностью и любовью.
Однако, сколько людей, столько и мнений. У каждого своя правда.
Существуют также интересные теории о связи между формой или сечением линии и ее характером.
Форма, как и цвет, является свойством объекта. Формат — это обзор видимого объекта, отражающий его пространственное сложение (forma, в переводе с латинского — внешний вид). Все вокруг нас имеет форму. Задача художника — понять и изобразить их конструктивную структуру и смысловое содержание. И мы, как зрители, должны уметь читать образы, чтобы расшифровать природу и смысл различных форм. Формы создаются на бумаге и на экране компьютера путем обнаружения линий. Поэтому характер форм зависит от характера образующихся линий.
Какие из этих линий могут представлять спокойствие, гнев, безразличие, волнение или радость?
На этот вопрос нет простого ответа. Например, колючая проволока может олицетворять гнев, веселье или неистовую радость, доходящую до границ безрассудства.
Какое настроение или эмоция соответствует каждой из этих строк?
Как форма зависит от характера линии, которую она образует?
Повторение ранее изученного материала
Декартова система координат
Поэтому эта система координат имеет два законных названия. Первый из них — Cartesiani, название, полученное от фамилии автора. А второй менее интересный и обоснованный — в прямоугольной системе координат, происхождение этого названия становится очевидным после взгляда на систему координат. Угол между двумя водилами равен 90°, его часто называют прямым углом, отсюда и второе название.
Вопросы
- Что такое отрезок?
- С чего состоит отрезок?
- Как можно найти середину отрезка?
- Кузнецов А. В., учитель математики (5-9 класс), г. Киев
- «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
- Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
- Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»
Задать вопросы о современном образовании, высказать идеи и решить наболевшие проблемы можно на Учебном форуме — международной конференции свежих мыслей и свежих действий. Создавая блог, вы не только повышаете свою репутацию компетентного учителя, но и вносите значительный вклад в школы будущего. Гильдия лидеров образования открывает двери для ключевых профессионалов и побуждает их к совместной работе по созданию лучших школ в мире.
Действительно, соотношение выполняется, то есть отрезок в три раза короче отрезка. Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
Середина отрезка. Координаты середины отрезка
Середина отрезка является точкой отрезка и равна конечной точке.
Часто в геометрических задачах необходимо найти носитель пространства, заданный координатами его конечностей. В поиске проблемы через центральную линию.
Каждая координата средней части отрезка равна половине суммы соответствующих координат его конечностей.
Примечание: Конвенция «сечение в 1,5 раза меньше «эквивалентного» сечения и в 1,5 раза больше сечения».
Середина отрезка на плоскости
Исходные данные: x a, y a и b x b, y b даны две произвольные несмежные точки O x y, две произвольные несмежные точки. Точка C — центр участка a. Требуется определить координаты x c и y c точки C.
Рассмотрим случай, когда точки A и B не совпадают и не находятся на одной линии координат, или не являются прямыми перпендикулярами к одной из осей. A x, A, B x, B y, C x, C y — проекции (прямые o и o y) точек a, b и c на координатные оси.
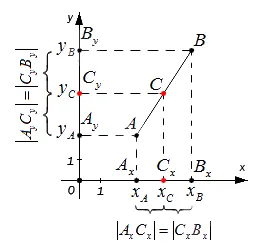
Согласно структуре, прямые a x, b x и c x параллельны. Линии также параллельны друг другу. Поэтому, согласно теореме Талиса, из уравнения A c = C b получаются следующие уравнения: a x c x = c x b x и a c y = c y b y, и они доказывают, что c x — центр оси. Секция A X B X и c y занимает центральное место в секции A Y B. Затем, основываясь на типах, которые появились ранее, мы имеем
x c = x a + x b 2 и y c = y a + y b 2
Тот же тип можно использовать, если a и b — прямые с одинаковой координатой или линейно перпендикулярны одной из осей. Мы не будем подробно анализировать этот случай, а рассмотрим его только графически.
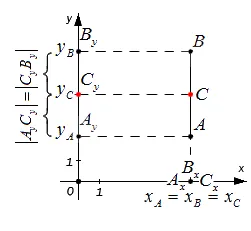
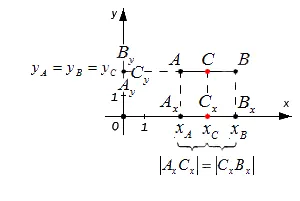
Обобщая вышесказанное, координаты среднего из отрезков a b уровня с координатами конечностей A (x A, y a) и B (x b, y b) определяются следующим образом
Середина отрезка в пространстве
Исходные данные: система координат O X Y Z и две произвольные точки с заданными координатами A (X A, Y A, Z A) и B (X B, Y B, Z B). Найдите координаты точки C в середине отрезка a.
a x, a y, a z, b x, b y, b z, c x, c y, c z — проекции всех точек на оси системы координат.
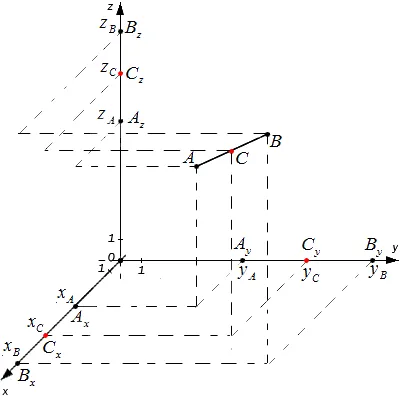
Согласно теореме Талиса, применимы следующие уравнения: a x c x = c x b x, a y c y = c y b y, z c z = c z b z.
Таким образом, точки c x, c y и c z являются отрезками a x b x, a y b y и z b z соответственно. Затем этот тип применяется для определения координат средней точки сечения в пространстве.
x c = x a + x b 2, y c = y a + y b 2, z c = z a + z b 2
Полученный тип также применим, если точки A и B являются прямыми перпендикулярами к одной из линейных координат и к одной из осей и находятся на одном уровне координат или перпендикулярны к одному из уровней координат.
Определение координат середины отрезка через координаты радиус-векторов его концов
Тип нахождения координат среднего значения отрезка может происходить в соответствии с алгебраической интерпретацией вектора.
Исходные данные: точки заданы в картезианской прямоугольной системе координат o x y, a (x a, y a) и b (x b, x b) координаты. Точка c — центр отрезка a.
Согласно геометрическому определению действия на вектор, имеет место следующее: o c→ = 1 2 -o a→ + o b→. В данном случае точка C является пересечением прямоугольных диагоналей, построенных на векторе A→ B→, т.е. средними точками диагонали. Координаты вектора пятна равны координатам точки и применяются следующие уравнения: a→= (x a, y a), β→= (x b, y b). Давайте выполним некоторые действия над вектором координат.
o c→= 1 2 -o a→ + o b→= x a + x b 2, y a + y b 2
Таким образом, точка c имеет координаты.
По аналогии, этот тип определяется для нахождения координат части сечения в пространстве
c (x a + x b 2, y a + y b 2, z a + z b 2).
Затем с помощью компаса начертите два круга радиуса AB с центрами A и B.
Параметры середины отрезка в пространстве
Чтобы выделить основные типы решений этих проблем, необходимо рассмотреть конкретные примеры.
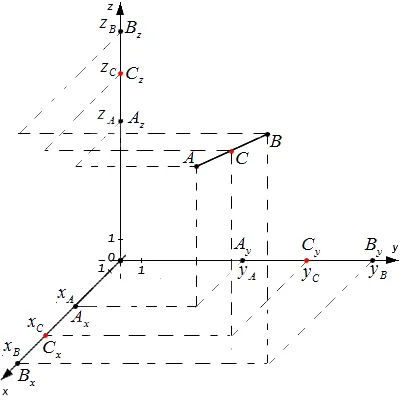
Рисунок 4: Координатная система с тремя координатами.
Согласно фундаментальной теореме Фалеса, все уравнения равны. Таким образом, значение C равно 3 — средней точке каждого уровня координат.
Можно составить и вывести окончательное уравнение для определения средней точки линии в координатной плоскости, состоящей из трех или более осей.
Это уравнение также можно применить, если точки A и B лежат на одной из координатных прямых. Или по прямой линии, перпендикулярной одной из осей. Точки также могут находиться в одной координатной плоскости, перпендикулярной одной из координатных плоскостей.
Исходные данные: x a, y a и b x b, y b даны две произвольные несмежные точки O x y, две произвольные несмежные точки. Точка C — центр участка a. Требуется определить координаты x c и y c точки C.
Определение координат середины отрезка через координаты радиус-векторов его концов
Тип нахождения координат среднего значения отрезка может происходить в соответствии с алгебраической интерпретацией вектора.
Исходные данные: точки заданы в картезианской прямоугольной системе координат o x y, a (x a, y a) и b (x b, x b) координаты. Точка c — центр отрезка a.
Согласно геометрическому определению действия на вектор, имеет место следующее: o c→ = 1 2 -o a→ + o b→. В данном случае точка C является пересечением прямоугольных диагоналей, построенных на векторе A→ B→, т.е. средними точками диагонали. Координаты вектора пятна равны координатам точки и применяются следующие уравнения: a→= (x a, y a), β→= (x b, y b). Давайте выполним некоторые действия над вектором координат.
o c→= 1 2 -o a→ + o b→= x a + x b 2, y a + y b 2
Таким образом, точка c имеет координаты.
По аналогии, этот тип определяется для нахождения координат части сечения в пространстве
c (x a + x b 2, y a + y b 2, z a + z b 2).
Примеры решения задач на нахождение координат середины отрезка
Среди проблем, связанных с использованием приведенной выше формулы, есть как те, которые касаются непосредственно вычисления координат среднего из отрезков, так и те, которые связаны с приведением условий для этого запроса. Часто используется термин «медиана». Цель — найти координаты одного конца отрезка. Также часто встречается проблема симметрии, решение которой обычно не вызывает проблем после изучения предмета. Давайте рассмотрим типичный пример.
Исходные данные: точка на плоскости с координатами A (-7, 3) и B (2, 4). Найдите координаты среднего значения отрезков A и B.
Центр отрезка AB обозначен точкой C. Его координаты определяются как половина суммы координат краев отрезка, то есть точек A и B.
x C = x A + x B 2 =-7 + 2 2 =-5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
ОТВЕТ: координаты средней части отрезка AB равны 52 и 72.
Данные: известны координаты треугольника A B C: A (-1, 0), B (3, 2), C (9, -8). Найдите длину медианы AM.
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C. В первую очередь найдем координаты середины отрезка B C, т.е. точки M :
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (-8)2 =-3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М ), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М :
A M = (6-(-1))2 + (-3-0)2 = 58
Исходные данные: в декартовой системе координат в 3-мерном пространстве дан параллелограмм A B C D A 1 B 1 C 1 D, даны координаты точки C 1 (1, 1, 0) и точки M. В центре параллелограмма BD 1 мы имеем координаты M (4, 2, -4). Вычислите координаты точки A.
Параллельные диагонали пиратов пересекаются в точке, которая является средней из всех диагоналей. На основании этого утверждения можно отметить, что точка m, известная под вопросом, является средой раздела A C 1. По типу нахождения координат центрального сечения в пространстве находим координаты точки A: x m = x a + x c 12 ⇒ xa = 2 -x m -x c 1 = 2-4-1 + 7 y m = y a + y c 1 2 ⇒ ya = 2 -y m -y c 1 = 2-2-1 = 3 z m = z a + z c 12 ⇒ za = 2 -z m -z c 1 =. 2-(-4) — 0 = -8
Ответ: координаты точки А (7, 3, -8).
Команда опытных редакторов и исследователей приняла участие в подготовке этой статьи и проверила ее точность и полноту.
Количество источников, использованных в этой статье: 7. Их список можно найти внизу страницы.
Команда управления контентом WikiHow тщательно следит за работой редакторов, чтобы каждая статья соответствовала установленным нами высоким стандартам качества.
Углы могут быть разделены посередине, как секции. Деление посередине — это деление чего-либо на две равные части. Существует два способа разделить угол посередине. Если у вас есть такой прибор, вы можете использовать угломер. Вы также можете использовать прибор для измерения углов, если он у вас есть. В качестве альтернативы можно использовать линейку и компас для деления угла.








