Решение задач по математике онлайн. Как решить тригонометрическое неравенство?

Содержание

Если в уравнении или неравенстве есть только сумма синуса и косинуса и произведение синуса и косинуса и все возможные, или, то мы можем подставить.

Урок по теме «Решение тригонометрических неравенств»

Тема тригонометрических неравенств объективно сложна для усвоения и понимания учащимися 10 класса. Поэтому очень важно последовательно разобраться в алгоритме, от простого к сложному, и выработать твердый навык. решения тригонометрических неравенств.

Успех в изучении этого предмета зависит от знания основных определений и свойств тригонометрических и обратных тригонометрических функций, знания тригонометрических формул, умения решать Целочисленные и дробно-рациональные неравенства, основные формулы. тригонометрических уравнений.

Особое внимание следует уделить методам преподавания решения простейших тригонометрических неравенств, поскольку каждое тригонометрическое неравенство сводится к решению элементарные неравенства.

Основное представительство о решении простейших тригонометрических неравенств желательно вводить с помощью графиков синуса, косинуса, тангенса и котангенса. Только после этого изучаются неравенства в круге. решать тригонометрические Неравенства в круге.

Я опишу основные этапы аргументации при решении простейших тригонометрических неравенств.

Находим на окружности точки, синус (косинус) которых равен данному числу.
В случае строгого неравенства отмечаем на окружности эти точки, как выколотые, в случае нестрогого – как заштрихованные.
Точку, лежащую на главном промежутке монотонности функции синус (косинус), называем Р_t1, другая точка — P_t2.
Отмечаем по оси синусов (косинусов) промежуток, удовлетворяющий данному неравенству.
Выделяем на окружности дугу, соответствующую данному промежутку.
Определяем направление движения по дуге (от точки Р_t1 в точке P_t2 в дуге ), мы показываем стрелку в направлении движения, над которой пишем символ «+» или «-» в зависимости от направления движения. (Этот шаг важен для проверки найденных углов. Учащиеся могут проиллюстрировать распространенную ошибку в определении границ пространства на примере решения неравенства по графику синуса или косинуса и по окружности ).
Находим координаты точек Р_t1 (в виде дуги или дуг с заданным числом) и напишите P_t2т.е. границы интервала, проверьте правильность нахождения углов с помощью t₁и t_2.
Записываем ответ в виде двойного неравенства (или промежутка) от меньшего угла до большего.

Рассуждения при решении уравнения для тангенса и котангенса аналогичны.

Рисунок и запись решения, которые должны находиться в тетрадях учащихся, перечислены в предлагаемом конспекте.

Конспект урока по теме: «Решение задач тригонометрических неравенств”.

Целью урока является дальнейшее изучение следующих тем решения тригонометрических Уравнения, включающие функции синуса и косинуса, переход от более простых к более сложным уравнениям.

Оборудование: диаграммный проектор, карточки для рисования круга. тригонометрических Доска, флипчарт, карточки с заданиями по неравенствам. заданием.

Форма организации урока — преподавание. Методы обучения, используемые на уроке — устные, наглядные, репродуктивные, исследование проблем, индивидуальные и фронтальные вопросы, устная и письменная самопроверка, самостоятельная работа.

(Задания и ответы написаны на кодовой ленте, я открываю ответы по одному. решения)

Выделенная дуга на рисунке представляет собой сумму всех элементов, выполняющих конкретное неравенство. Концы этой дуги являются частью искомого множества. Их расстояния равны -1/2, поэтому они удовлетворяют неравенству.

Немного теории.

Пусть дано простейшее неравенство $ \sin x > a $. 1) С $-1 1 $ решениеm неравенства — любое действительное число: $ x \in \mathbb $ 3) Если $a = 1 $ решениеm неравенства — любое действительное число, кроме $ \frac<\pi> + 2\pi k, \; k \в \mathbb $ 4) Если $a \leqslant -1 $ неравенство не имеет вида решений.

Пусть дано простейшее неравенство $ \cos x > a $. 1) При $-1 1$ решениеНеравенство m — любое действительное число: $ x \in \mathbb $ 3) Для $a \leqslant -1$ неравенство не имеет вида решений. 4) При $a = 1$ решениеm неравенство — любое действительное число, кроме $ 2\pi k, \; k \in \mathbb $.

Неравенства вида $ tg \;x > a $ и \( tg \;x

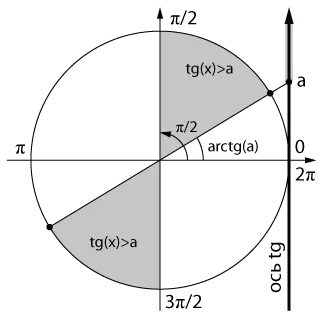
Пусть дано простейшее неравенство $ tg \;x > a $. Множество всех решений данного тригонометрического неравенства, которые мы можем решить с помощью тригонометрического Круг. Из этого рисунка видно, что для каждого $a \in \mathbb. $ решение Неравенства будут. \;\; \Frac<\pi> + \pi k

ight), \; k \in \mathbb $.

Неравенства вида $ ctg \;x > a $ и \( ctg \;x

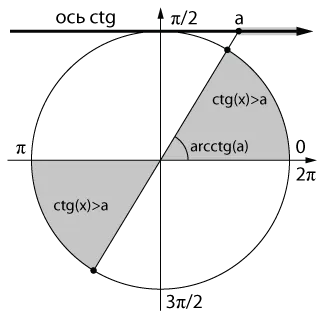
Пусть дано простейшее неравенство $ ctg \;x > a $. Множество всех решений данного тригонометрического неравенства, которые мы можем решить с помощью тригонометрического Круг. Из этого рисунка видно, что для каждого $a \in \mathbb. $ решение круг. Из этого рисунка для каждого \(a \in \mathbb.

Неравенства будут.

Учитывая простое неравенство \( ctg \;x

О тригонометрических Запишите значение $\frac$ на оси косинусов и определите интервал, в котором это значение больше $\frac$. Затем определите интервал для точек, для которых неравенство выполняется. решения

Неравенства: Значение, типы и характеристики тригонометрической функции.

Тригонометрические уравнения — это уравнения, в которых переменные зависят только от знака

При доказательстве тригонометрических Тригонометрические функции обозначаются следующим образом:

Уравнения Применение общих методов доказательства алгебраических неравенств.

Осторожно. Если преподаватель обнаружит плагиат в вашей работе, вам не избежать значительных проблем (вплоть до отчисления). Если вы не можете написать работу самостоятельно, закажите ее здесь.

В тригонометрии, однако, спектр прикладных математических методов богаче.

метод от обратного;
аналитико-синтетический метод;
методы математического анализа;
метод математической индукции;
элементы геометрии;
векторная алгебра;
графический метод.

Виды тригонометрических неравенств

К ним относятся:

В тригонометрии существует два типа неравенств:

По признаку однородности они делятся на два типа:

В однородных неравенствах все слагаемые имеют ту же степень, что и сумма.

Примерами таких неравенств являются:

Простейшие

Простейшие тригонометрические В неоднородных случаях степени слагаемых отличаются друг от друга.

Неравенства имеют вид:< m, sin x >sin x < m, cos x >m, cos x < т, tg x >m, ctg >m, tg x < m,

где m — заданное число.

Сложные

В сложных тригонометрических m; ctg

\(sin 3x — sin x >неравенства, аргументом функции неравенства является целочисленное выражение с неизвестным, а не просто переменная.

$cos x — 5x + 2 > 0; $

Методы решения тригонометрических неравенств

Общие сведения по решению тригонометрических неравенств

При решении тригонометрических 0.\) тригонометрических Неравенства используют свойство монотонности

функций и их интервалов устойчивости.

Монотонность является характеристикой как убывающих, так и возрастающих функций. Это означает, что в пределах данного интервала большее или меньшее значение члена соответствует большему или меньшему значению функции, в зависимости от того, является ли значение функции возрастающим или убывающим.

Чтобы решить простейшее тригонометрическое Об интервалах известных констант говорят, если набору значений аргумента соответствуют только положительные или только отрицательные значения функции.

Важные моменты в решении простейших тригонометрических неравенств:

Чтобы решить неравенство, нужно найти множество всех значений аргумента, которые превращают данное неравенство в допустимое числовое неравенство.

sin x = 0, если $\mathrm x=\mathrm, \ R\in Z;$

sin x = -1, если $x=-\frac\pi R+2\pi R\, \ R\in Z;$

sin x = 1, если $x=\frac\pi2+2\pi R, \ R\in Z;$

для cos x:

cos x = 0, если $x=\frac\pi2+\pi R,\ R\in Z;$

cos x = -1, если $x=\frac2+2\pi R,\ R\in Z;$

cos x = 1, если $x=2\pi R,\ R\in Z;$

Касательная не существует, если $x=\frac\pi2+\pi R,\ R\in Z;$. решения тригонометрических Нестандартные способы

Графический метод.
Метод постановки.
Метод интервалов.
Метод секторов.
Метод концентрических окружностей для систем тригонометрических неравенств.

Для решения простейших тригонометрических неравенств, используются различные методы: решения и решение неравенства с использованием графического метода

Решение тригонометрических неравенств с помощью единичной окружности

Решите неравенство: sin x >с помощью числового круга.

½.

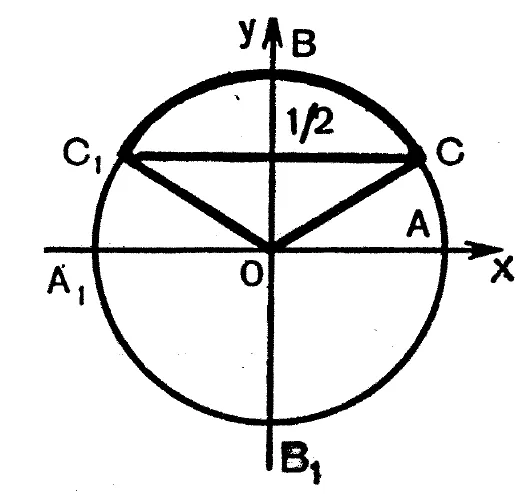
Нарисуем единичную окружность. Начертите на ней дуги AC и $AC_1$. Их синус должен быть равен ½.

Чтобы получить все решения Окружность показывает, что все дуги, начинающиеся в точке A и заканчивающиеся в любой внутренней точке дуги $CBC_1$, удовлетворяют этому неравенству.

этого неравенства, добавьте 2πR к концам этого интервала.Реакция.

Решите неравенство: cos 3x >с помощью числового круга.

½.

Обозначим 3x через a.

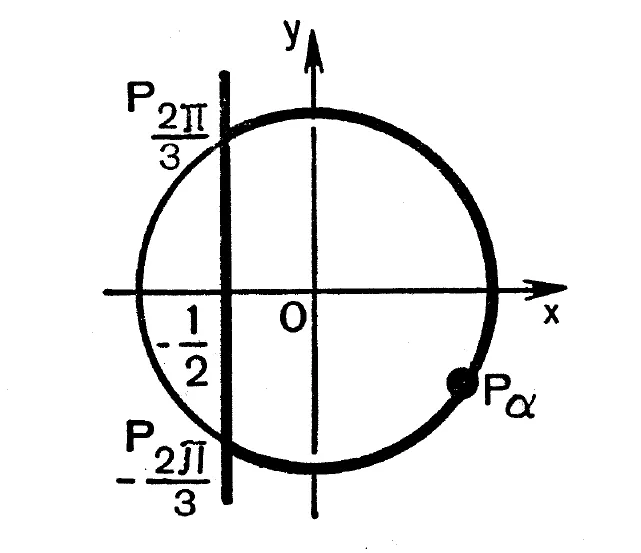
Неравенство будет иметь вид:

Все точки \P_\alpha\ единичной окружности, дистальное положение которых больше или равно -1/2, удовлетворяют этому неравенству.

Выделенная дуга на рисунке представляет собой сумму всех элементов, выполняющих конкретное неравенство. Концы этой дуги являются частью искомого множества. Их расстояния равны -1/2, поэтому они удовлетворяют неравенству.

Отмеченная дуга на рисунке представляет собой множество всех точек, удовлетворяющих этому неравенству. Края этой дуги являются частью искомого множества. Их расстояния равны -1/2, поэтому они удовлетворяют неравенству. решения для неравенства

Учитывая периодичность косинуса, мы пишем<2\pi>\(-\frac<2\pi>3+2\pi R\leq\alpha\leq\frac

3+2\pi R, \ R\in Z.\)

Решите неравенство: tg 2x >Если мы еще раз вернемся к переменной x, то получим искомый ответ:

1. шаг решения, (Обсуждение. На доске назовите по одному ученику.