Заменив эти значения в уравнении, получаем 2 * 2-4 = 0 в левой части. При этих значениях левая часть (ноль) не равна правой части (т.е. 3). Считается, что пара чисел x = 2 и y = 4 не удовлетворяет уравнению или не является решением уравнения.
Уравнение с двумя неизвестными, формулы и примеры
Системы уравнений и отдельные уравнения используются для решения сложных и необходимых задач. При решении конкретной задачи необходимо составить два уравнения, каждое из которых содержит две неизвестные величины. Другими словами, есть два уравнения с двумя неизвестными.
Вам нужно найти такие значения чужих X и Y, которые удовлетворяют первому уравнению и второму уравнению одновременно. Это означает, что каждое уравнение должно быть преобразовано в соответствующее равенство. Иначе: необходимо найти общее решение обоих уравнений. Альтернативно, решите систему этих уравнений.
Если можно найти общие решения двух или более уравнений, то эти уравнения называют системой. Объедините их в скобку, чтобы создать систему уравнений.
— Система имеет бесконечное число решений.
Каждое уравнение в системе имеет бесконечное число решений, и только одна пара чисел является общей в обоих уравнениях.
Решением системы уравнений с двумя переменными является пара переменных переменных, которая преобразует каждое уравнение системы в истинное равенство.
- ПРИМЕР:
- Приведённую выше систему уравнений удовлетворяет пара чисел :
- х = 15;
- у = 5.
Вот решение для этой системы. Другого решения нет.
Существуют уравнения с бесконечным числом решений и системы без решений. Системы без решений называются несовместимыми. Решения системы нельзя назвать корнями.
- Решить систему – это значит найти все решения этой системы или показать, что она не имеет их.
- Две системы уравнений называются равносильными ( эквивалентными ), если все решения одной из них будет решением другой, и наоборот, все решения другой системы будут решениями первой.
- ПРИМЕР:
Пары чисел: x = 4 и y = 3. Эти числа также являются единственными решениями системы.
Таким образом, рассмотренные системы уравнений эквивалентны.
Две несовместимые системы уравнений также считаются эквивалентными. Два равных уравнения могут состоять из одного и того же числа и разных уравнений. Кроме того, система уравнений эквивалентна одному уравнению. Актуально понятие эквивалентности систем уравнений: две системы уравнений эквивалентны для одного набора чисел и не равны в другом уравнении.
- Теоремы про равносильность систем уравнений первой степени.
- ТЕОРЕМА
- Любое из уравнений системы можно заменить равносильным ему уравнением ; полученная в результате этого система равносильна данной.
- ПРИМЕР:
Если вы замените второе уравнение его эквивалентным уравнением, то вы
вы получаете новую систему, эквивалентную данной.
Решите систему уравнений:.
Решение:.
- Система не имеет решений, так как два уравнения системы не могут удовлетворяться одновременно ( из первого уравнения
- х + y = 3,
- а из второго
- х + y = 3,5).
- ОТВЕТ: решений нет
- ПРИМЕР:
Урок «Уравнения с двумя неизвестными»
БЕСПЛАТНО
Большинство математических задач сосредоточено на решении типичных уравнений с переменными. Можно использовать более одной системы уравнений, каждая из которых может включать более двух переменных.
Однако следует изучать простые уравнения с двумя неизвестными абстрактными выражениями, отличными от арифметических выражений. Например:.
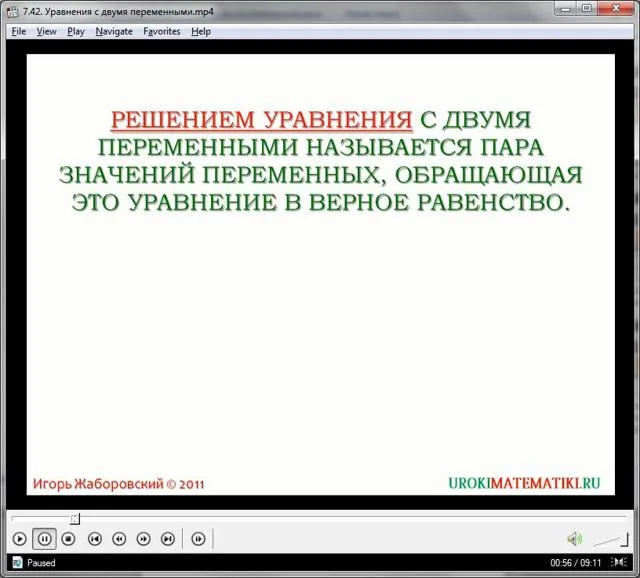
Каждое такое уравнение называется уравнением с двумя переменными. Решением такого уравнения является пара цен, x и y, которые обращаются вправо, где все выражение одинаково. Используем такие значения для переменных.
- х = 2
- у = 1
- Подставляя в наше уравнение, получим верное равенство:
- х2 + 2у = 6
- (2)2 + 2(1) = 6
- 4 + 2 = 6
- Таким образом, пара чисел (2, 1) являются решением для уравнения.
x2 + 2u =6. Обратите внимание, что при записи решения необходимо указать значения переменных для разделенных сторон и записать значение x первым (это не строго, но разрешено).
- Решая первый пример методом подбора, легко найти ещё одну пару решений – например, воспользуемся значениями (4, -5):
- х2 + 2у = 6
- (4)2 + 2(-5) = 6
- 16 – 10 = 6
- Пара чисел превратила уравнение в правильное равенство, значит, она так же соответствует решению данного уравнения.
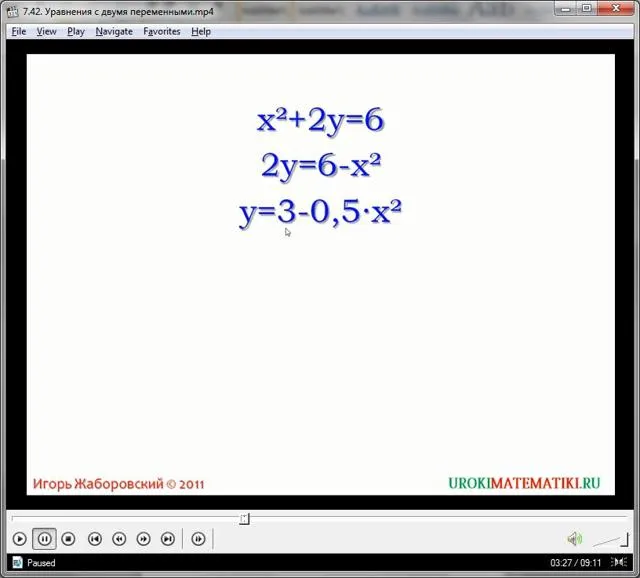
Как можно понять из видеоурока, уравнение с двумя переменными имеет множество решений, а точнее, множество пар чисел, которые удовлетворяют критериям правильного решения. Превратите первое уравнение в следующее. Разделите все части уравнения на 2.
Как помнится из видеокурса по основам функций, каждая зависимость характеризуется тремя элементами: набором некоторых начальных аргументов, типом преобразования и набором получаемых значений.
В нашем уравнении каждый фактический набор решений представлен парой цен X и Y, т.е. парой элементов из обоих наборов функций. Само уравнение является выражением взаимосвязи между первой и второй переменными.
Более того, уравнение Y = 3-0,5×2 имеет точно такие же пары решений, как и x2 + 2u = 6. Следовательно, эти уравнения называются равными. В этих случаях имеют место эквивалентные уравнения:.
- При осуществлении переноса слагаемых (с учетом инверсии знака) с одной части равенства в другую;
- При различных тождественных преобразованиях, не меняющих смысл равенства;
- При умножении или делении одновременно обеих частей уравнения на один и тот же коэффициент;
Важно понимать, что выполнение различных преобразований уравнений не должно деформировать область определения переменных. Большинство преобразований тождеств не должны изменять x или y в целом, но есть неприятные исключения. Рассмотрим один из таких примеров:.
1.8 Простейшие системы уравнений с двумя неизвестными
Видеоурок 1: Два уравнения с двумя незнакомцами
- Видеоурок 2: Решение систем уравнений
- Лекция: Простейшие системы уравнений с двумя неизвестными
- Уравнения с двумя неизвестными
В этой связи рассмотрим уравнение с участием двух незнакомцев. Во многих случаях для решения этого типа уравнений требуется столько же уравнений, сколько и неизвестных.
Уравнения с двумя незнакомцами имеют следующий вид
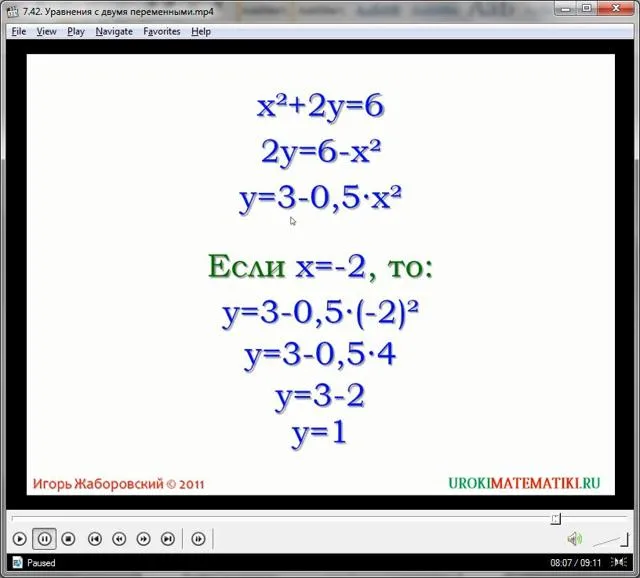
- a, b, c, d — это числа, стоящие рядом в переменными (х, у) .
- Решить систему уравнения — это означает найти такое значение переменных, которые приведут оба уравнения в верное равенство.
- Каждое из уравнений может иметь несколько ответов, однако ответом на систему уравнений будет та пара чисел, которая будет подходить обоим уравнениям.
- Трактовать решение системы уравнений можно аналитическим способом, некоторые из которых мы рассмотрим позднее, и графическим способом.
- Графический способ решения системы уравнений
Для каждого указанного уравнения можно построить свой собственный график на уровне. Это может быть любой из известных графиков функции. Решением системы уравнений является точка пересечения графиков. Эти точки имеют координаты, которые соответствуют упорядоченным и FAR позициям, которые затем становятся решениями.
Из графика могут вытекать различные типы решений
1. набор решений. Например, если одно уравнение представляет собой тригонометрическую функцию, а второе уравнение — прямую линию. Параллельно оси OA эта линия пересекает график второй функции из набора периодичности.
2. решение. В этом случае графики функций пересекаются в одной точке. Обычно это происходит, когда график уравнения представляет собой прямую линию.
3. два решения. Это означает, что график уравнения пересекается в двух точках. Обычно это наблюдается, когда график одной из функций представляет собой притчу.
4. нет решения. Некоторые функции могут вообще не пересекаться. В этом случае у системы нет решения.
Основные методы аналитического разрешения.
Не всегда легко решить задачу с помощью графиков, так как точки пересечения могут находиться далеко от начала или иметь дробные координаты. Для наиболее точного нахождения решения системы целесообразно использовать метод детального решения.
После этого обмена одно из уравнений становится неизвестным, и уравнение решается известным способом. Когда одна из переменных найдена, ее значение заменяется в первом уравнении, и вторая переменная также заменяется.
2. как добавлять или удалять уравнения
Этот метод позволяет удалить одного из незнакомцев. Теперь представьте, что вы хотите удалить переменную ‘X’.
Чтобы этот метод работал, нужно добавить D к первому уравнению и A ко второму. Тогда у вас будут те же коэффициенты, что и у переменной ‘x’.
Уравнения не дают окончательного ответа на поставленную задачу. Она лишь показывает отношения между двумя незнакомцами. Исходя из этой взаимосвязи, зная цену одного из незнакомцев, мы могли бы также найти цену другого.
Решение уравнений с двумя неизвестными
В математике большинство задач сосредоточено на решении типичных уравнений, в которых представлены переменные. Однако в некоторых из них, помимо арифметического уравнения, одновременно участвуют два незнакомых человека. Прежде чем приступить к решению таких уравнений, стоит рассмотреть их определение.
Таким образом, уравнение с двумя незнакомцами является равенством следующего вида
a*x + b*y = c, где a, b и c — числа, а x и y — неизвестные переменные.
Вот несколько примеров.
Уравнения с двумя неизвестными имеют решения так же, как и уравнения с неизвестными. Однако такие выражения обычно имеют бесконечно много различных решений, которые обычно не могут быть определены в алгебре.
Решение задач
Чтобы решить такую задачу, нужно найти пару цен для x и y, которая удовлетворяет ей. Другими словами, преобразуйте уравнение Незнакомые X и Y в правильное арифметическое уравнение. Используйте метод подбора, чтобы найти удовлетворительные пары чисел.
Чтобы пояснить объяснение, давайте найдем корни выражения: y-x = 6.
Для y = 5 и x = -1 уравнение дает тождество 5 — (-1) = 6. Поэтому пару чисел (-1; 5) можно рассматривать как корень из y-x = 6. (-1; 5).
Следует отметить, что ответ должен быть записан в скобках с точками сверху и снизу. Сначала должно быть записано значение x.
Уравнения такого рода могут не иметь корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9
Преобразуйте исходное уравнение в следующий вид: x+y = x+y+9.
В результате получается неверное равенство, и поэтому выражение не имеет корней.
При решении уравнения можно использовать свойства уравнения. Первый заключается в том, что вы можете перенести все обобщения в другую часть уравнения. В то же время вы можете изменить знак уравнения на противоположный. Полученное уравнение соответствует исходному уравнению.
Например, из уравнения 20y -3x = 16 неизвестное y переносится в другую часть уравнения.
Оба уравнения эквивалентны.
Второе свойство: части уравнения можно умножить или разделить на одно и то же число, которое не равно нулю. Полученные уравнения равны.
Эти два уравнения также эквивалентны.
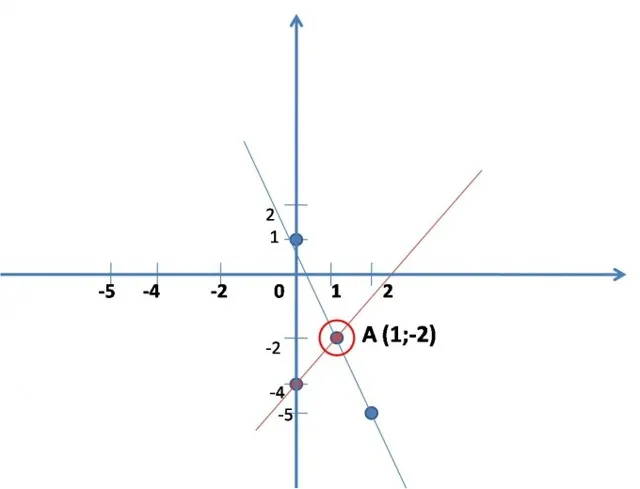
Система уравнений с двумя неизвестными
Система уравнений — это множество равенств, выполняемых одновременно. В большинстве задач требуется найти решение системы, состоящей из двух уравнений с двумя переменными.
Чтобы решить систему уравнений, нужно найти числа, которые преобразуют оба уравнения системы в подходящие равенства. Решением может быть пара чисел, много пар чисел или вообще ни одного.
Подобные системы уравнений могут быть решены следующими методами
Метод подстановки
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
Если вы найдете корни всех этих методов и одну и ту же систему, вы должны получить тот же эффект, если вы все сделали правильно.
Сегодня, используя инструменты, встроенные в программу Excel Office, специальные веб-ресурсы и калькуляторы, вы можете решать подобные задачи. С их помощью можно легко контролировать точность расчетов и результатов.
Мы надеемся, что эта статья поможет вам понять основные принципы школьной математики. Если вы все еще не можете справиться с этим типом решения уравнения, не расстраивайтесь. Чтобы понять и принять изучаемый предмет, рекомендуется как можно больше практиковаться. Таким образом, вы сможете с легкостью решать сложные задачи. Удачи вам в ваших математических завоеваниях!
При необходимости умножьте уравнение системы на множитель так, чтобы коэффициенты одной из переменных были противоположными числами.
Уравнения с двумя переменными
Одно уравнение с двумя переменными является решением (x, y) системы двух линейных уравнений с двумя посторонними. Подстановка этих чисел в уравнения системы превращает каждое уравнение системы в действительное равенство. .
Рассмотрим уравнение с двумя переменными f (x; y) = 0. Пара пар переменных, которые преобразуют уравнение с двумя переменными, называется решением уравнения. Учитывая уравнение с двумя переменными x и y, общепринятой практикой является сначала установить значение переменной x, а затем установить значение y на второе место в записи этого решения.
Таким образом, пары (10; 0), (16; 2) и (-2; -4) являются решениями уравнения x -z = 10. В то же время, пара (1; 5) не является решением задачи Уравнение.
Существуют и другие решения этого уравнения. Чтобы найти их, удобно выразить одну переменную через другую. x на x, получив уравнение x = 10 + zu. Выбрав любое значение y, можно рассчитать соответствующее значение x. Например, если y = 7, то x = 10 + 3 * 7 = 31, следовательно, пара (31; 7) является решением уравнения — если y = -2, то x = 10 + 3(-2) = 4, следовательно, пара (4; -2) также является решением данного уравнения.
Уравнение с двумя переменными называется равновесным, если оно имеет одно и то же решение (или оба не имеют решения).
Для уравнений с двумя переменными теоремы 1 и 2 (см. 135) применимы к эквивалентным преобразованиям уравнений.
Пусть уравнение в двух переменных f (x; y) = 0. Если все решения представлены точками на уровне координат, то существует множество точек на плоскости. Это множество называется графиком уравнения f(x; y) = 0.
Например, графиком уравнения (см. рис. 1.10); графиком уравнения у — х = 0 является прямая (биссектриса первого и третьего координатных углов, см. рис. 1.8); графиком уравнения у — 3 = 0 является прямая, параллельная оси х (рис. 1.108), а графиком уравнения х + 2 = 0 — прямая, параллельная оси у (рис. 1.109). Графиком уравнения
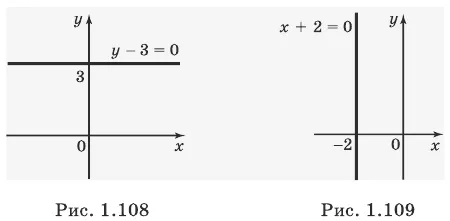
Линейное уравнение с двумя переменными и его график
Уравнения вида — числа, линейные? числа в переменных, — свободные члены.
Графиком любого линейного уравнения , то эта прямая параллельна оси у, если
Пример:
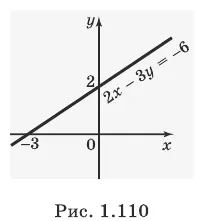
Постройте график уравнения 2x -3u = -6.
График этого линейного уравнения представляет собой прямую линию. Достаточно знать две точки, в которых строится прямая. Вместо x получаем -Zu = -6, что заменяет значение 2x -3u = -6. Здесь y = 2. Вместо y в 2x — 3u = -6 подставляем значение 0 и получаем 2x = -6. Следовательно, x = -3.
Таким образом, на графике найдены две точки (0; 2) и (-3; 0). Построив их прямо, получим график уравнения 2x -Zu = -6 (рис. 1.110).
Если линейное уравнение имеет вид 0 * x + 0 * y = c, могут возникнуть два случая.
(1) c = 0 — в этом случае уравнению удовлетворяет любая пара (x; y), поэтому графиком уравнения является весь уровень координат.
2)
Эта лекция взята из полной программы лекций по математическому предмету.
См. также дополнительные лекции по математическим предметам.
Отправляйте задания днем и ночью.
Официальный сайт Брилиджоно Банаталия Валерия Эванта Екатеринбургского государственного педагогического института.
Все права интеллектуальной собственности на загруженный материал сохраняются за бенефициарами этого материала. Коммерческое и/или иное использование запрещено за пределами материалов предварительного изучения NataliblileNova.ru. Публикация и распространение опубликованных материалов не предназначены для получения коммерческой и/или иной выгоды.
Этот сайт предназначен для облегчения образовательного пути студентов. Наталья Брилёнова не предлагает и не оказывает товары и услуги.
Для получения копий материалов обязательно сообщать онлайн-ссылку на сайт Natalibrilenova.ru.








