Решите задачу: Лицензированный бассейн объемом 3000 литров необходимо заполнить водой. Сколько литров воды необходимо вылить в бассейн за два часа. Это гарантирует, что бассейн будет заполнен более чем наполовину через два часа и не переполнится через три часа.
Неравенства и системы неравенств с двумя неизвестными
Решите неравенство между двумя незнакомыми людьми, плюс их система кажущаяся Рассмотрим алгоритм, который может легко решить эту задачу.
Предположим, что существует неравенство с двумя незнаками $ y $, $ \ le $, $ \ ge $).
Все решения таких неравенств могут быть выражены на уровне координат. Сделайте следующее:.
Выберите одну из этих областей и рассмотрите любую. Убедитесь, что исходное неравенство применимо к этой точке.
- Если неравенство выполняется, следовательно, оно выполняется и для всей области, из которой выбирали точку. Таким образом, область, в которой лежит выбранная точка и есть множеством решений неравенства.
- Если неравенство не выполняется, то множество решений неравенства – область, в которой не лежит выбранная точка.
В случае строгого неравенства граница области, являющаяся точкой на графике $ y = f(x)$, не входит в множество решений, а предел изображается пунктирной линией. В случае нестрогих неравенств границы областей включаются в набор неравных решений, а ограничения показываются в виде компактных линий.
Покажите все точки заданного графика с неравенством $ XY> 3 $.
Постройте график функции $ XY = $ 3. Для этого разделите обе части уравнения на $ x $. Это связано с тем, что его нельзя преобразовать в ноль. Это объясняется тем, что уравнение (произведение количества нулей не может быть равно $3):.
График полученной функции является преувеличенным и делит уровень координат на две области: одна — между преувеличенной ветвью и ветвью за ней; другая — между преувеличенной ветвью и ветвью за ней.
Выберите любую точку в одной из областей. $(1; 2)$ с координатами.
Замените его координаты неравенством: $(1; 2)$.
Следовательно, точка в выделенной области не является решением данного неравенства. Поэтому решение неравенства — это еще одна область, где не было выбрано ни одной точки.
Поскольку это неравенство является строгим, предельная точка — точка на графике функции y = 3/x — нарисована пунктирной линией. Обозначьте все точки графика, которые составляют решение данного неравенства.
Готовые работы на аналогичную тему
Система неравенств с двумя неизвестными
Рассмотрим пример решения системы неравенств с двумя незнакомцами.
Покажите все точки графика, заданного системой неравенств
Постройте график функции, соответствующей данному неравенству.
Нарисуйте непрерывную функцию $ x^2+y^2 = $ 49. Это соответствует нестрогому неравенству, линия 3500x+y = $ 5 с пунктирными линиями.
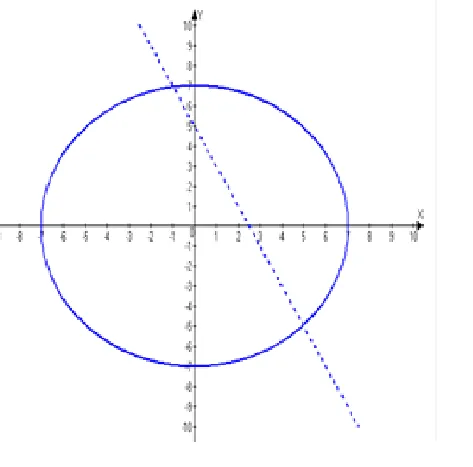
Рассмотрим каждое неравенство отдельно.
Первое неравенство — $ x^2+y^2 \λ49$.
Найдите $(5; 8)$ на графике этой функции. Проверьте правильность неравенства.
$89≤49$ — неравенство неверно.
Поэтому решением данного неравенства является область, в которой выбранная точка не находится, то есть область круга.
Второе неравенство — 3500x+y>5$.
Получите $(4; 3)$ на графике этой функции. Проверьте правильность неравенства.
Поэтому решением этого неравенства является область, в которой находится выбранная точка, т.е. область над прямой.
Исследования. Если альпинист увеличит свою скорость на 1 км/ч, то расстояние в 4 км до вершины холма он преодолеет быстрее, чем за 2 часа. Если скорость снижается на 1 км/ч, альпинист не достигает вершины за 2 часа. С какой скоростью движется альпинист? Решение: получить AS.
Решение систем неравенств с одной переменной

В этом уроке представлена концепция неравных систем с использованием переменных и их решений. Развивать навыки решения систем неравенства. Научитесь записывать решения в системе уравнений, используя геометрическую интерпретацию в виде числового пространства.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам по комплекту, необходимо приобрести его в каталоге и добавить в личный кабинет.



Конспект урока «Решение систем неравенств с одной переменной»
Решите задачу: Лицензированный бассейн объемом 3000 литров необходимо заполнить водой. Сколько литров воды необходимо вылить в бассейн за два часа. Это гарантирует, что бассейн будет заполнен более чем наполовину через два часа и не переполнится через три часа.

Если в двух неравенствах с одной переменной нужно найти такое значение x, которое верно одновременно, запишите их вместе и скажите, что они образуют систему неравенств.
Скобки показывают, что в обоих неравенствах системы нужно найти значение x, которое преобразуется вв допустимое числовое неравенство..
Система, созданная для решения этой задачи, является примером системы линейных неравенств с одной переменной.
Решением системы неравенств с одной переменной является такое значение переменной, при котором каждое неравенство в системе верно.
Двойные неравенства также могут быть описаны как системы.
Решить систему неравенств — значит найти все ее решения или доказать, что решений нет.
Рассмотрим несколько примеров решения линейных систем неравенств с одной переменной.
Пример 1: Решение системы неравенств.

Пример 2: Решение системы неравенств.

Пример 3: Решите систему неравенств.

Пример 4: Решите систему двойных неравенств.

Напишите алгоритм решения системы линейных неравенств с одной переменной.
Чтобы решить систему неравенств, используйте.:.
1. решите каждую систему неравенств.
2. нарисуйте множество решений каждого неравенства с линией координат.
3. найти пересечение пространств (если таковое имеется) и описать его как символ пространства, или как неравенство, определяющее пространство, или сделать вывод, что система не имеет решения.
Пользователи дополнительных материалов, пожалуйста, не забывайте оставлять свои комментарии, замечания и предложения. Все материалы контролируются антивирусной программой.
Тонкости решения систем неравенств в задаче 15
В этом видео представлен подробный разбор довольно серьезной задачи15 из Единого государственного конкурса по математике, включающей логарифмические и дробные неравенства. Особое внимание уделяется теореме Беза (для нахождения корней многочленов) и технике деления многочленов на углы (умножение).
Предмет решает две системы неравенств из Единого государственного конкурса по математике.
⎪⎩⎨⎪7log7-2x(x + 6)≤0x-x-3 x + 6-x 2 + 27x + 90 x 2 +8x+12≤-1Ѓ слева Ѓ< \begin& <<\log >_> \ слева (x + 6 \ справа) ߡ le 0 \ & x- \ frac- \ frac ^> + 27x + 90> ^> + 8x + 12> \ le -1 \\\\\ end \ справа.
Решение системы неравенств
Как видите, система состоит из логарифмического неравенства и дробного неравенства, но в процессе решения видно, что это неравенство не так просто, как кажется. Начнем с логарифмов. Для этого мы опишем их отдельно.
Как и в случае с другими логарифмическими неравенствами, эта конструкция сводится к обычной форме. То есть, в левой части все остается без изменений, а в правой части записывается следующим образом
Как использовать метод рационализации
Здесь используйте метод рационализации. Если у вас есть неравенства формы, вы можете
После этого можно приступать к строительству.
\ɑLeft (f \left (x
ight) — g \left (x
ight) ɑLeft (k \left (x
ight) — 1
ight) ɑBigcup 0
Конечно, в этом неравенстве не учитывается площадь логарифма: площадь логарифма не учитывается.
Эти неравенства должны быть вычислены отдельно, а затем пересечены со вторым решением. В принципе, однако, рассмотрение ЭФК при решении логарифмических неравенств не дает, поэтому вернемся к решению элементов системы.
Применение метода интервалов
Таким образом, f(x)f \left (x
ight) — линейная функция x+6 x+6, а g(x)g \left (x
ight) — просто 1. Поэтому перепишем логарифмическое неравенство системы следующим образом:.
\ᢙLeft (x+6-1 \Right) ᢙLeft (7-2x-1 \Right)
Последняя 1 — это x-1 x-1 во второй скобке. Когда выполняется это преобразование, все становится меньше или равно 0. Признаки неравенства сохраняются. Аналогично для всех кронштейнов.
\ЈLeft (x+5 \Right) ЈLeft (6-2x \Right) ЈLe 0< >Очевидно, что мы имеем дело с простым неравенством, легко разрешимым с помощью пространства. Приравняем скобку к 0.
Отметим все эти точки (таких точек две) в прямых координатах. Обратите внимание, что они заштрихованы: они не заштрихованы.
Обратите внимание на табличку: она находится в тени. Для этого возьмите число больше 3. Первым символом будет отрицательный символ. В этом случае знаки будут чередоваться везде, так как шкала кратности отсутствует. Нас интересует наименьший или знак равенства, то есть знак «минус». Заштриховываем нужную область. Напомним, что при решении неравенств методом интервалов мы заменяем 1 на последнее полученное выражение, прежде чем перейти к уравнению.
Итак, вы нашли набор. Но, как видите, это все еще не решение проблемы неравенства. Далее необходимо найти диапазон логарифмов. Для этого напишите следующие функции
Неправильное построение равных
Ключевые моменты
\ слева \ начало&x+6> 0 \&7-2x> 0 \&7-2x \ ne 1 \ конец \ справа.=> \ слева \ начало&x> -6 \&7> 2x \&6 \ ne 2x \ конец \ справа.=> \ слева \ начало&x&x3.5 \&xne \ текст.
- Нужно уметь решать логарифмические неравенства с помощью перехода к канонической форме.
- Нужно уметь работать с дробно-рациональными неравенствами. Это вообще материал 8-9 класса, поэтому если вы работаете с логарифмами, то уж с дробно-рациональными неравенствами разберетесь.
- Теорема Безу. Важнейшим следствием из этой теоремы является тот факт, что корни многочлена с целыми коэффициентами являются делителями его свободного члена.
3 \ конец \ право.
Таким образом, существует три одновременных требования. Это означает, что все эти неравенства должны выполняться одновременно. Проведите параллель с ответом кандидата.< b и c < d, то а + c < b + d. Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять, т.к. возможны исключения. Например, если из 12 >Получены окончательные ответы по первому пункту в системе.
Линейные неравенства с двумя переменными
\모 слева (-6; -5 \ справа) ߄ bigcup \ слева (3; 3,5 \ справа). В этот момент многие студенты задают вопросы. Он окрашен. Как бы вы охарактеризовали результат? Правильно, и запомните простое правило для всех этих вопросов.
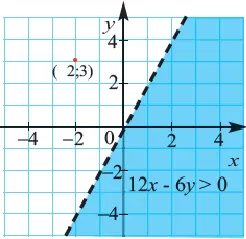
Что вы имеете в виду под разрезом? Это множество, которое является членом как первого, так и второго целого. Другими словами, при заполнении рисунка ниже мы ищем такие точки, которые принадлежат одновременно первому и второму рядам. Следовательно, если точка не принадлежит хотя бы одной из этих линий, она нас не удовлетворяет, как бы она ни выглядела во второй линии. В частности, в строке 3 история выглядит следующим образом. С одной стороны, точка 3 удобна для кандидатов на ответ, так как она заштрихована, но с другой стороны, она вписана в логарифмический ряд. Поэтому эта точка также должна быть вписана в окончательный набор. Это делает ответ на первое логарифмическое неравенство в системе совершенно верным. Для убедительности повторю еще раз: логарифмическое неравенство системы не является проблемой.
В этом вопросе необходимо отметить ряд важных моментов.
• Если неравенство выражается знаками
В остальном это довольно громоздкая, шаблонная система решения проблем. Некоторые трудности в решении системы могут возникнуть и на пересечении всех множеств, особенно множеств, относящихся к точке 3. Это очень легко сделать. Помните, что рассечение означает, что все неравенства должны выполняться одновременно. Все три оси должны быть охвачены. Если хотя бы одна ось не является общей или вместе с вырезом, эта точка не может быть частью ответа.
2. Нарисуем график уравнения
Если a> b и c> d, то a + c> b + D
Если из 8 вычесть 3>2, ответ будет 9>6; если из 7>2 вычесть 12>8 вычесть 12>8 вычесть 12>8 вычесть 12>8 вычесть 12>8 вычесть 7>2, ответ будет неверным.
1. Определим уравнение в точке . По точке . То есть из уравнения получим
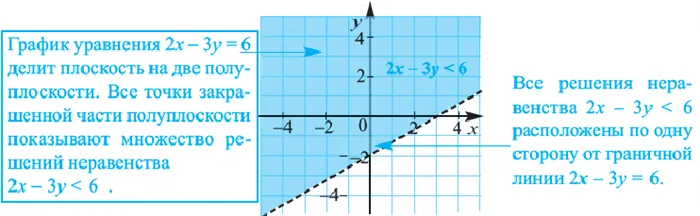
Уравнение линии границы: , не входят во множество решений неравенства. Выберем пробную точку , правая часть
Левая часть То есть, закрашенная часть на рисунке является множеством решений неравенства
Неравенство — это линейное неравенство с двумя переменными. Решение неравенства — это пара декартовых систем координат, которые могут отображать все решения линейного неравенства с двумя переменными. Например, множество решений неравенств, образующих границу.
-Для проверки правильности выбора полууровня, соответствующего решению неравенства, выберите контрольную точку на каждом полууровне. Заштрихуйте полуплоскость, на которой расположены точки, удовлетворяющие неравенству.

Математическая запись:
1. Чтобы решить неравенство, выразим , получим и
-Если неравенство представлено точкой, оно изображается пунктирной линией.
3. Любые целые значения , взятые из закрашенной части, являются решением этого неравенства. Точка случаю, когда все билеты были куплены для взрослых. А также любая точка, взятая из закрашенной части удовлетворяет неравенству
Системы линейных неравенств с двумя переменными
Решением системы линейных неравенств с двумя переменными называется множество пар чисел
Пример 1.

1. решите неравенство относительно переменных
3. проверьте неравенство относительно точки. Правая часть неравенства равна нулю. Неравенство есть и другая сторона неравенства есть.
Пример 2.Запишите неравенство, соответствующее графику.
4. Выберем отсюда одну точку, например

Каждая пара
Пример 2. Изобразите графически на координатой плоскости неравенство
Приложение работает.
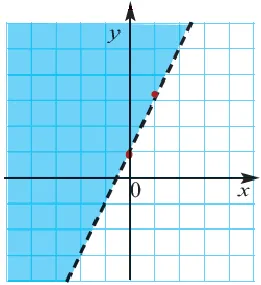
2. Изобразим неравенство Все точки полуплоскости, расположенные правее от этой прямой будут решениями неравенства
3. Изобразим неравенство , нарисуем в прямоугольной системе координат пунктирной линией. Все точки полуплоскости, расположенные левее от этой прямой будут решениями неравенства
4. Часть плоскости, соответствующая неравенствам на координатной плоскости.
5. Проверка: проверим в точке

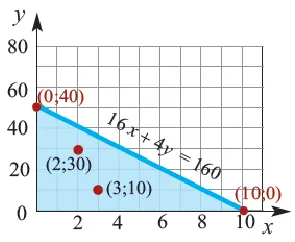
Пример 1.Взрослый билет в театр стоит 16 манатов, а детский — 4 маната. Сумма, собранная от продажи билетов в кассе, не превышает 160 манатов. Различные варианты количества проданных билетов. Числовая информация и переменные, соответствующие рассматриваемой ситуации: 1.
2. раскрасьте фигуру, заданную графиком и координатными осями.
1. использовать пограничные линии и изобразить соответствующую область синей линией.
2) Решение неравенства и часть полуплоскости, расположенная ниже этой прямой. Решение неравенства и часть полуплоскости, расположенная ниже этой прямой. Решением системы
3. С помощью пробной точки
2. с помощью уравнения α, соответствующая область обозначена красной линией.
(3) Множество решений системы неравенств будет частью плоскости, заштрихованной обоими.
1. напишите двойное неравенство.
График системы линейных неравенств, соответствующий реальной ситуации, почти всегда представлен в первой четверти координатной плоскости.
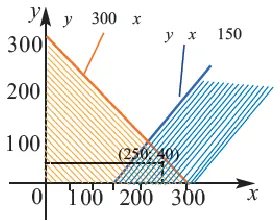
Пример 3.Один из двух конвейеров производит контейнеры из нержавеющей стали, а другой — медные контейнеры. Когда каждый конвейер работает на полную мощность, в день производится менее 300 сковородок. В связи с высоким спросом на кастрюли из нержавеющей стали, ежедневно производится больше кастрюль из нержавеющей стали, чем медных кастрюль, но более 150 кастрюль. Составьте неравенство, показывающее количество произведенных контейнеров в день, и постройте его график.
Решение: 1) Предположим, что количество медных контейнеров. В зависимости от проблемной ситуации можно написать следующую систему неравенств








