Поскольку квадратный корень арифметический существует только из неотрицательных чисел, последнее равенство имеет смысл только в том случае, если ( — c / a) ≥ 0. Заключение: заключение.
Корни уравнения как найти
Основными уравнениями школьной алгебры являются линейные и квадратные. Все остальные уравнения могут быть приведены к различным преобразованиям тождеств или путем соответствующих обменов.
Пример 1. Решите уравнение — x + 5,18 = 11,58. решение: -x + 5,18 = 11,58— x = -5,18 + 11,58— x = 6,4- x = -6,4. ответ: -6,4.
Пример 2: Решите уравнение 3-5(x + 1) = 6-4x. Решение: 3-5(x + 1) = 6-4x -3-5x -5 = 6-4x -5x + 4x = 5-3 + 6— x = 8- x = -8. 8.
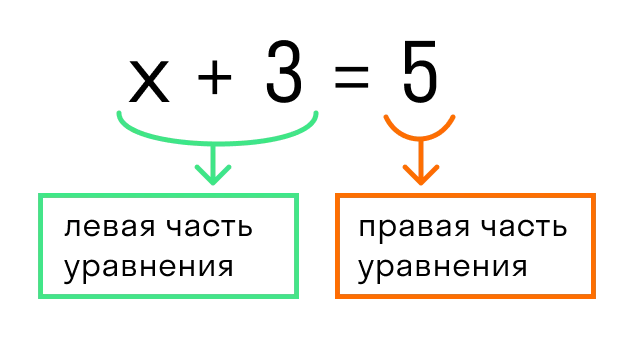
Умножьте обе части уравнения на 6. Вы получаете уравнение, равное исходному уравнению. 2x + 3 (x -1) = 12, 2x + 3x -3 = 12, 5x = 12 + 3, 5x = 15, x = 3. Ответ: 3.
Пример 4. Решите систему решений: из уравнения 3x -y = 2 найдите y = 3x -2 и замените его уравнением 2x + 3u = 5.
Получите 2x + 9x -6 = 5, 11x = 11 и x = 1. ПРИМЕЧАНИЯ. Если неизвестными в системе являются x и y, то ответ можно записать в виде координат точки.
Квадратные уравнения
Для d нет решения.< 0. При решении квадратных уравнений полезно помнить формулу чётного коэффициента, т.е. случай, когда b = 2k или k =b/2:

Пример 5. Решите уравнение 3u + y 2 = y. Решение: 3u + y 2 = y — неполное квадратное уравнение — y 2 + 3u- y = 0- y 2 + 2u = 0-y∙(y + 2) = 0.
Помните! Если хотя бы один фактор равен нулю, то один из них равен нулю, а другой имеет смысл. y1 = 0, или y + 2 = 0- y2 = -2. Ответ: -2? 0.
Пример 6.Уравнение 18 -x 2 = 14.Решение: 18 -x 2 = 14- Неполное квадратное уравнение — x 2 = 14-18- x 2 = -4- x 2 = 4- x = ±2.Ответ: ±2.
Пример 7. Решите уравнение x 2 + 6x -3 = 2x 3. Решение: x 2 + 6x -3 = 2x 3 — уравнение трех степеней. Решите методом умножения: x 2-2x 3 + 6x -3 = 0- x 2 (2x -1) + 3 (2x -1) = 0- (2x -1) (3 -x 2) = 0- 2x — 1 = 0 или 3 -x 2 = 0- x1 = 0.5; х2.3 =. Ответ: 0,5; .
Пример 8. Решите уравнение (x 2-5x) 2-30 (x 2-5x) — 216 = 0. Решение: (x 2-5x)2-30 (x 2-5x)-216 = 0 является двух — фетгонным уравнением. Такие уравнения можно решить методом обмена.
ПРИМЕЧАНИЯ. Метод обмена позволяет перейти к уравнению, эквивалентному данному уравнению. Пусть x 2-5x = t. Тогда уравнение становится t 2-30t -216 = 0.

x 2-5x = -6 или x 2-5x = 36- x 2-5x + 6 = 0 или x 2-5x -36 = 0. По теореме Виета: x1 = 2, х2 = 3, х3 = -4, х4 = 9. Ответы: -4, 2, 3, 9.



Ответ:

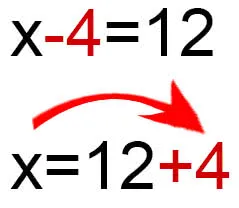
x + y = -7/2 не удовлетворяет условиям задачи, так как хотя бы одно из слагаемых этого итога не является прямым.
Рациональные уравнения
При решении логических уравнений необходимо исключить неизвестные величины с обнуляемыми знаменателями.

Поле уравнения x -2≠0. В этом случае левая часть уравнения может быть уменьшена на ().

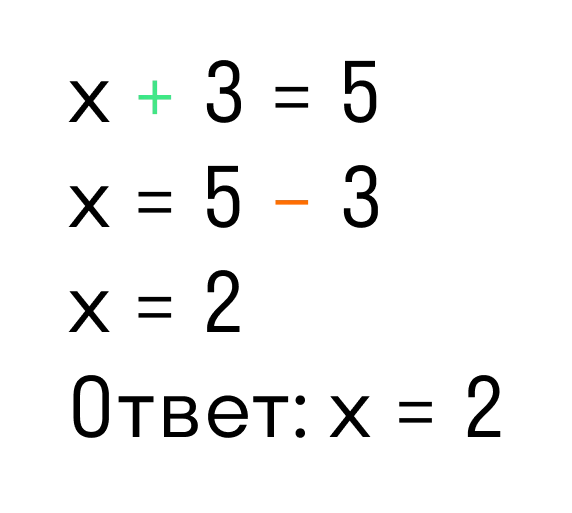


Поскольку x 2 +5 не равно нулю, уравнение равно Уравнение 3 (x 2 +5)2 -23 (x 2 +5)-8 = 0. Пусть x 2 +5 = t.
x 2 +5 ≠ -1/3. Остается x 2 +5 = 8- x 2 = 3- x =. Ответ.
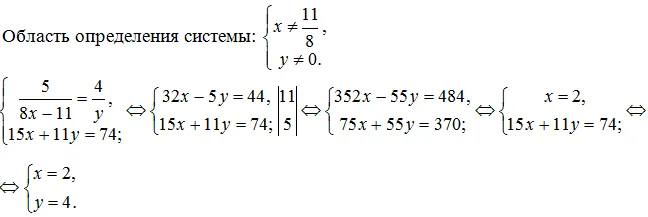
Теорема 1: Если уравнение некоторое время возрастает (убывает), то это уравнение может иметь в этот момент не более одного корня.
Решение квадратных уравнений
Квадратные уравнения изучаются в 8 классе, поэтому в них нет ничего сложного. Совершенно необходимо знать их решения.
— Это уравнение вида a, b + c = 0. где коэффициенты a, b и c — произвольные числа, а ≠ 0.
Прежде чем рассматривать конкретные методы решения, отметим, что все квадратные уравнения можно разделить на следующие три категории.
В этом заключается важное различие между квадратичными и линейными уравнениями: корни всегда единственны. Как определить количество корней в уравнении? Для этого существует замечательная вещь, называемая идентификацией.
Дискриминант
Предположим, что квадратное уравнение ax2+ bx + c = 0. Тогда оно становится просто числом D = b2-4ac.
Мы должны знать это уравнение извне. Откуда он берется, сейчас не важно. Важно то, что по знаку дискриминанта можно определить количество корней квадратного уравнения. В частности.
Примечание: Знак отличия показывает количество корней, а не знак, как многие почему-то думают. Посмотрите на пример, и вы убедитесь в этом сами:.
Запишите коэффициенты первого уравнения и найдите различие: α = 1, β = -8, γ = 12- D = (-8)2-4 —1-12 = 64-48 = 16
Следовательно, дискриминант положителен и уравнение имеет два разных корня. Аналогично анализируется второе уравнение: α= 5, β= 3, γ= 7, Δ= 32-4-5-7 = 9-140 = -131.
Дискриминантное уравнение отрицательное и не имеет корней. Осталось последнее уравнение: α= 1, β= -6, γ= 9, Δ= (-6)2-4 -1-9 = 36-36=0.
Дискриминант уравнения равен нулю — корень есть.
Обратите внимание, что коэффициенты записываются на каждое уравнение. Да, это занимает время, да, это утомительно — но зато вы не путаете тарифы и не делаете глупых ошибок. Выберите скорость или качество.
Кстати, когда вы привыкнете к этому, через некоторое время вам не нужно будет записывать всех вкладчиков. Вы будете функционировать таким образом в своем сознании. Большинство людей начинают делать это примерно после 50-70 уравнений, что не так уж и много.
Корни квадратного уравнения
Теперь перейдем к фактическому решению. Если знак D>0, то корни можно найти с помощью следующего уравнения
![]()
Основные уравнения для корней квадратных уравнений
Если D = 0, вы можете использовать любое из этих уравнений. Вы получите одно и то же число, которое и является ответом. Наконец, если D< 0, корней нет — ничего считать не надо.
Первое уравнение: x 2 —2 x -3 = 0 => a = 1, b = -2, c = -3, D = (-2) 2 —4 -1- (-3) = 16.
D>0 ⇒ Уравнение имеет два корня. Найдите их:.
![]()
Второе уравнение: 15-2 x-x 2=0 => a = -1, b = -2, c = 15, D = (-2)2 —4 -4 -(-1)-15 = 64.
D>0 ⇒ Уравнение снова имеет два корня. Найдите их.
Наконец, третье уравнение: x 2 + 12 x + 36 = 0 ⇒ a = 1, b = 12, c = 36, D = 12 2-4 —1 —36 = 0.
D = 0 ⇒ Уравнение имеет корни. Можно использовать любой тип. Например, первый:.
Как видно из примера, все очень просто. Вам нужно знать только уравнение и как его рассчитать. Самая распространенная ошибка возникает при замене отрицательного коэффициента в формуле. И здесь вам поможет приведенный выше прием: буквально посмотрите на уравнение, запишите каждый шаг, и вы быстро избавитесь от ошибки.
Для того чтобы уравнение имело корни разных знаков, одновременно необходимы и достаточны два условия: 1) D / 4> 0 (в зависимости от типа коэффициента баланса) — 2) x1 ∙ x2 < 0 (по теореме Виета):
Классификация уравнений
Каждое уравнение имеет свои правила и алгоритмы решения. Можно выделить следующие типы уравнений: алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и т.д.

В некоторых формулах значение корня может быть записано в виде функции или функции параметров. Для решений используются специальные функции анализа. Это может дать информацию для вычисления корней и предварительного определения их количества и зависимости от значений параметров. Однако аналитическое решение может быть применено только к алгебраическим уравнениям (до четвертого порядка).
Для трансцендентных уравнений количество аналитических решений ограничено, поскольку не все тригонометрические значения равны нулю. Если подробное решение не может быть найдено, используется метод расчета. Пространство, в котором расположены маршруты, может быть ограничено. Поэтому такие решения не являются точными.
Алгебраический тип
Уравнения вида P(x1, x2. xn) = 0, где многочлен представлен неизвестным аргументом, называются алгебраическими. Они могут содержать одно или несколько неизвестных и иметь оценку.
Существуют различные типы алгебраических уравнений, включая линейные, квадратичные, кубические и двудольные (четвертого порядка). Линейные также могут быть объединены в системы. Решение линейного уравнения означает нахождение общего корня всех уравнений, входящих в него.
Линейные и квадратные
Линейные уравнения — это уравнения, степень которых соответствует 1. Они могут быть записаны в двух формах: общей и обычной. В первом случае форма такая: a1 * x1 + a2 * x2 + a * xn + b =0. Во втором случае число b нужно сдвинуть вправо: a1 * x1 + a2 * x2 + a * xn = b. Пример: 3x-2=25.

Более сложные выражения считаются квадратными уравнениями. То есть, уравнения A * x 2 + B * x + C = 0 (A не равно 0). Они могут быть полными (A, B и C не равны 0) и неполными (некоторые факторы равны 0, кроме A). Они могут быть решены автоматическими и ручными методами.
Для нахождения корней квадратных уравнений можно использовать специальное программное обеспечение или онлайн-ресурсы. Вам нужно ввести значения A, B и C в специальные поля. Программа рассчитывает все за одну секунду и выдает результат. В последнем случае необходимо применить уравнение. Корни квадратного уравнения вычисляются путем нахождения делителя и подстановки значений A и B в уравнение. Чтобы найти их, необходимо следовать алгоритму.
Другой способ — применить теорему Виета, которая верна только при A = 1. Корни можно найти с помощью следующих уравнений: x1 + x2 =—B и x1*x2 =C. Их также можно вычислить, построив чертеж график функции. Пересечение с осями является корнем.
Кубические и биквадратные
Многочлены с незнаками вида A * x 3 + B * x 2 + C * x + D = 0 называются кубическими уравнениями. A не может быть нулем; она решается с помощью кубической параболы.

Уравнение можно разделить на A и заменить на x = y- (b / (3 * A)). Исходное уравнение становится: y3+p * y + q =0. Коэффициенты p и q вычисляются следующим образом: q = 2 * B 3-9 * A * B * C + 27 * (A 2 ) * D / (27 * A 3) и p = (3 * A * C-B 2) / (3 * A 2).
При решении квадратного многочлена неизвестных каждый случай необходимо рассматривать отдельно. Заменяя переменные, все решается в деталях. Основная цель — снизить оценку.
С параметрами и трансцендентные
В области физики и математики можно найти уравнения с параметрами, от которых зависит их форма. Они могут быть линейными и нелинейными. Чтобы решить их, нужно найти все системы с параметрическими значениями, для которых существуют корни.

Пример — a*x + 1 =4. Параметр ‘a’ может быть дробью, вещественным или натуральным числом, или может состоять из суммы, произведения или разности определенных переменных. Допустимые значения зависят от состояния проблемы. Они называются лимитами.
Трансцендентные уравнения включают экспоненциальные, логарифмические, тригонометрические и обратные тригонометрические функции. Они не являются алгебраическими. Примерами являются cos(x) = x и lg(x) = x-5. Их корни определяются различными алгоритмами, которые опираются на общую форму. Допустимо использовать методы замены переменных для упрощения форм в процессе решения.
Линейные уравнения — это уравнения, степень которых соответствует 1. Они могут быть записаны в двух формах: общей и обычной. В первом случае форма такая: a1 * x1 + a2 * x2 + a * xn + b =0. Во втором случае число b нужно сдвинуть вправо: a1 * x1 + a2 * x2 + a * xn = b. Пример: 3x-2=25.
Как решать уравнения? Алгоритм действий.
Чтобы подвести итог рассмотренным нами проблемам с уравнениями, давайте рассмотрим некоторые общие правила решения уравнений.
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила применимы ко всем типам уравнений (линейные, квадратичные, логарифмические, тригонометрические, логические, иррациональные, экспоненциальные и другие типы). Поэтому важно понять эти простые правила и научиться их использовать.
You may also like:

Деление рациональных чисел примеры и правила.

Нужен репетитор по математике (алгебре) или геометрии?
Умножения рациональных чисел, математика, примеры.
Сложение рациональных чисел, правила и примеры.
Добавить комментарий Отмена ответа
Вы должны войти в систему, чтобы оставить комментарий.
Свежие записи
Если вы хотите продолжить работу над проектом, отключите блокировку рекламы или добавьте свой сайт в исключения блокировки.
Это правило подходит, когда все неизвестные и известные уже вычислены, но перед переменными остаются факторы. Примените правило увеличения или уменьшения коэффициентов уравнения несколько раз, чтобы удалить ненужные коэффициенты.
Начнем с конца
Когда я перечислял задачи, связанные с квадратными уравнениями, я делал это практически в том же порядке, в котором они изучаются в школе. Однако эта серия не оправдана с точки зрения обучения. Причины этого следующие.
Разрешение просто приводится в исходном виде (за редким исключением представления этих видов экспорта с помощью полного квадратичного уменьшения)
Очень мощная теорема Вайета представлена в конце только как эвристика для ее решения.
Гораздо проще начать с теоремы Виета.
Рассмотрим квадратный трином
Исходя из фундаментальной теоремы алгебры (которую очень трудно доказать, поэтому примем ее как данность), мы видим, что уравнение требует двух корней. Предположим, что это некоторые числа. Затем мы можем переписать исходное уравнение в виде выражения для его корней.
Эти уравнения эквивалентны, поскольку оба равны нулю (первое по умолчанию, второе — по построению).
Открыв скобу, можно увидеть следующее.
Отсюда, если соответствующие коэффициенты равны имеющимся коэффициентам, возникает известная система.
Мы доказали теорему Виета в случае квадратных треугольников. Это замечательный результат. Мы начинаем получать информацию о корнях, которые, как мы предполагаем, существуют. И это следующий результат, который мы будем использовать.
Геометрия параболы
Вершина
Здесь можно сказать весь первый курс алгебры в колледже: фокус, линия, конические сечения, первичные и вторичные производные …
Но поскольку мы были ограничены школьной программой (точнее, 7-8 классами), наши рассуждения просты.
С моей субъективной точки зрения, самый интересный аспект этой басни — ее вершина. Он однозначно определяет положение фабулы и то, как расположены корни.
Однако мы не знаем этой формулы. В среднем мы все еще находимся на расстоянии трех лет от первого зачатия деривативов. Они должны быть найдены.
Притча имеет симметричную форму. К моменту смещения относительно оси вал работает как симметричный вал. Когда начинается сдвиг, он продолжает быть симметричным, но уже прошел через верхнюю часть вокруг оси.
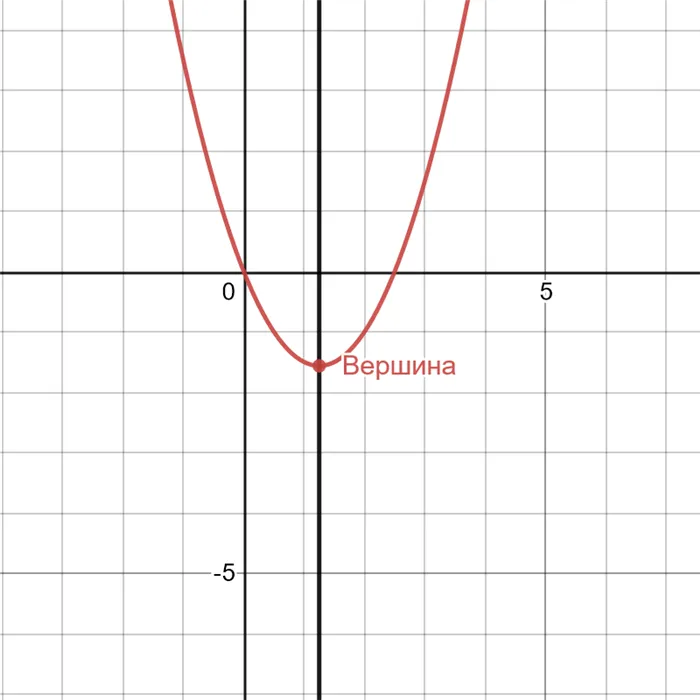
Притча о симметрии, верхняя часть, ось
Далее, расстояние от вершины до корня в обоих направлениях одинаково. Это означает, что верхняя часть притчи находится между корнями. Тогда координаты вершины являются средним значением ее корней
До сих пор мы не знаем корней. Но благодаря теореме Бето мы знаем, что такое сумма корней!
Это потрясающий результат, и мы можем его использовать.
Ещё немного про корни
Мы знаем, что корни, графики — это точки пересечения кривых. Это очень полезные знания. Потому что, рассматривая притчу чисто визуально, мы знаем, что возможны три случая.
Верхняя цена больше нуля и высокая скорость больше нуля
или верхнее значение меньше нуля, а высокий коэффициент меньше нуля.
Корень есть, но кратность равна двум (вспомните главную теорему алгебры), а верхняя цена равна нулю.
Второй случай тривиален; дойдем до третьего. Интересно взглянуть на математику первого из них. Найдем цену квадратного тринома в вершине: она равна нулю.
Затем посмотрите на первый случай. Притча висит на древке с веткой наверху.
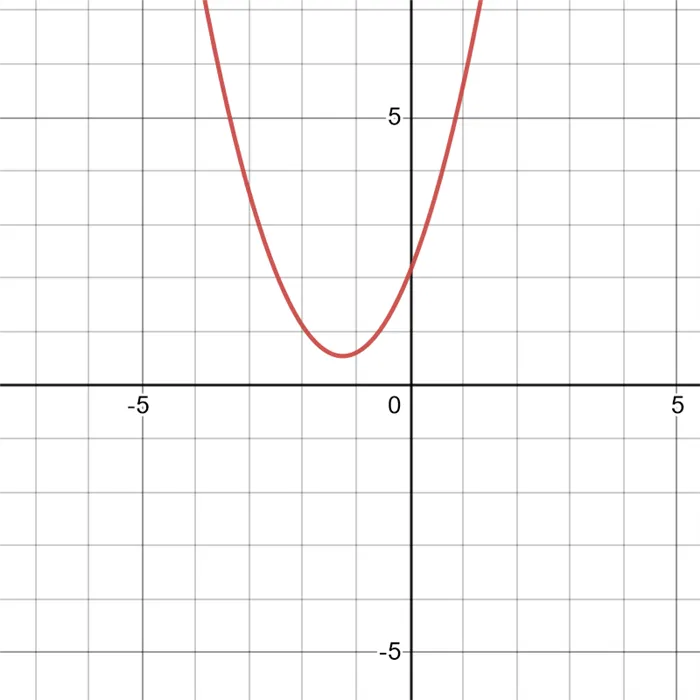
Первый случай.
Перемножим первое неравенство. Потому что знаки неравенства перевернуты:.
Это ситуация без корней.
Давайте кратко рассмотрим противоположный случай. Притча висит ветка за веткой.
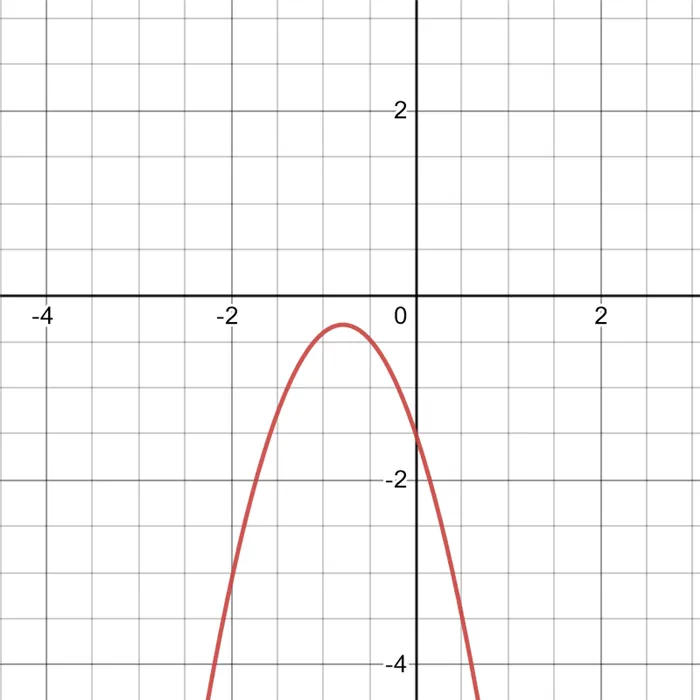
Второй случай.
Немного магии. Мы видим, что конвенция остается неизменной в отношении положения притчи. Но это лучше.
Обратите внимание, что на данный момент это всего лишь условие недействительного корня. Да, это похоже на скромные способности, но давайте предположим, что вы об этом не знаете.
Понятие дискриминанта
Мы уже многое узнали о корнях: они — часть корневой системы, они — часть актера, они — часть личности актера. Каковы они по отношению к актеру, каковы они по отношению к вершине, когда они не присутствуют. Все это очень полезно, но это еще не способ нахождения алгебраических цен.
Начнем с того, что мы уже знаем: с вершины. Каким-то образом, если бы мы знали расстояние между корнями, мы могли бы четко найти сами корни.
Что же мешает нам это сделать? Но давайте, как настоящие математики, найдем квадрат расстояния между корнями. Не теряя общности, мы предполагаем большие корни. Итак.
На данный момент это выглядит не очень хорошо, но похоже на то. Не понимаете, давайте сделаем идеальный квадрат, но на основе суммы, а не разницы. Давайте добавим его, но уберем, чтобы все осталось точно таким же.
Вы еще не видите? Воспользуемся теоремой Виета:.
Мы получили квадрат расстояния между корнями с учетом расширений во время фактора.
Теперь мы можем найти корни! Вершина притчи — это половина расстояния между корнями в обоих направлениях.
Квадрат расстояния между корнями в квадрате 3 является дискретной способностью.
В целом, ненавязчивый потенциал — это более сложное понятие, включающее в себя множество корней. Однако для квадратного уравнения в седьмом году этого достаточно.
Теперь, рассматривая ненавязчивую способность как расстояние, если оно равно нулю, то существует только один корень, а если оно отрицательно, то нет ни одного действительного корня.








