Как читаются многозначные числа? ОТВЕТ: Многозначные числа читаются слева направо. Число делится на классы по три цифры с конца, и всем цифрам, кроме нуля, присваивается имя. Цифра 0 при вводе номера означает отсутствие цифр.
Определение, что такое разрядные слагаемые с примерами разряда и класса в математике
Представленная здесь статья касается интересной темы натуральных чисел. Для выполнения некоторых операций необходимо представить исходное выражение в виде сложения многих чисел. Другими словами, цифры должны быть проанализированы численно. Обратный процесс также очень важен для упражнений и решения проблем.
В этом разделе подробно рассматриваются типичные примеры для лучшего усвоения материала. Вы также узнаете, как преобразовывать натуральные числа и записывать их в другом формате.
Сумма разрядных слагаемых натурального числа, в виде суммы разрядных слагаемых
Каким образом можно разложить число по разрядам?
Из названия статьи можно сделать вывод, что в этом параграфе рассматриваются такие математические термины, как «сумма» и «итог». Прежде чем изучать эту информацию, вам необходимо подробно изучить предмет, чтобы понять, что такое натуральные числа. Давайте приступим к работе и рассмотрим основные понятия суммы чисел.
Числовые сумматоры представляют собой несколько чисел, состоящих из нуля и одного ненулевого разряда. Номера 5, 10, 400 и 200 относятся к этой категории, а номера 144, 321, 5, 540 и 16 441 — нет.
Количество цифр в отображаемом номере равно количеству ненулевых цифр в записи. Это связано с тем, что выражение числа 61 как суммы арифметических слагаемых отличается от 6 и 1.
Если число 55050 анализируется как сумма чисел, то оно выражается как сумма трех итогов. Три пятерки, показанные в записи, отличаются от нуля. Обратите внимание, что сумма всех однозначных цифр числа содержит другое количество цифр в записи.
Сумма дополнительных цифр натурального числа равна этому числу. Давайте перейдем к понятию разрядных сумм.
Сложение числа — это такое натуральное число, что его файл содержит ненулевую цифру. Количество цифр должно быть равно количеству цифр, не равных нулю. Все кумулятивные числа могут быть записаны с разным количеством цифр. Когда число анализируется с помощью цифры, то сумма цифр всегда равна этой цифре.
Проанализировав концепцию, можно сделать вывод, что однозначные и многозначные числа (состоящие полностью из нулей, кроме первой цифры) не могут быть выражены в виде суммы.
Это происходит потому, что некоторые из этих чисел имеют одинаковое количество цифр. За исключением этих чисел, все остальные примеры могут быть разложены на суммы.
Как раскладывать числа?
Чтобы разложить число как сумму цифровых слагаемых, необходимо помнить, что натуральные числа связаны с определенным количеством элементов. Для числовых записей разложение зависит от количества единиц, десятки, сотни, тысячи и т.д.
Например, если мы возьмем число 58, то обнаружим, что оно соответствует десяти из пяти и восьми единиц. Число 134,400 соответствует 100,000, 30,000, 4,000 и 400.
Эти числа можно представить как равные -50 + 8 = 58 и 134 400 = 100 000 + 30 000 + 4 000 + 400. Эти примеры наглядно показывают, как числа можно разложить на числовые суммы. Примеры показывают, что любое натуральное число можно представить в виде суммы цифр.
Вот еще один пример. Представим натуральное число 25 в виде суммы цифр. Число 25 соответствует двум 10-балльным и одному 5-балльному, поэтому 25 = 20+5. Однако сумма 17+8 не является суммой 25 цифровых компонентов. Это связано с тем, что невозможно иметь два числа, состоящие из одинакового количества цифр.
Сумма разрядных слагаемых

Умение решать простые примеры в уме — полезный навык. Конечно, у вас всегда будет с собой смартфон, но гораздо лучше и эффективнее сделать это самостоятельно и гордиться собой. Существует множество приемов, позволяющих упростить умственные вычисления. Сложение чисел — один из них.
Эта статья поддерживается методистами SkySmart. Если вы обнаружили ошибку, обратитесь к интерактивной беседе (справа внизу на экране).
Сумма разрядных слагаемых
Каждое натуральное многозначное число может быть выражено как сумма цифровых компонентов. Сумма цифровых компонентов может быть записана как.
35 = 3 ТЭНС + 5 единиц = 3*10 = 30 + 5 = 35.
30 — сумма цифр — 5 — сумма цифр.
86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86
80 цифр Pumper — 5 цифр резюме.
356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300 + 50 + 6 = 356.
300, 50 и 6 — это сумма цифр.
Онлайн-курсы математики для детей помогают улучшить оценки и подготовиться к контрольным работам, IEP и экзаменам.
Разряды и классы чисел
Чтобы легко записывать числа в виде суммы цифр, учащиеся должны уметь правильно определять порядок и деление многих чисел.
В многозначных числах цифры справа налево делятся на группы из трех цифр. Эти группы называются классами.
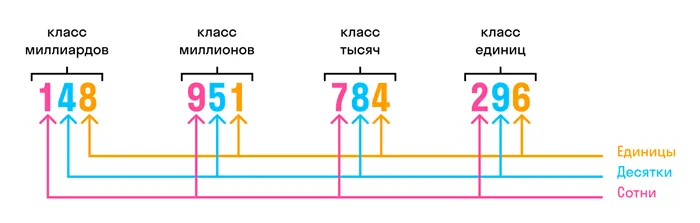
Название многозначного номера:.
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвёртый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.
Чтобы избежать преобразования многозначного числа при чтении в загадку, рекомендуется при записи определять число в классе. Следующее:.
Такие числа читаются слева направо.
Числа — это многозначные числа, в которых цифра занимает разряд.
Числа измеряются справа налево. Первая цифра справа от числа — это первая цифра.
- Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.
Числа — это единицы, десятки, сотни, миллионы и миллионы.
Все цифровые единицы, кроме простых, являются сложными единицами. На каждые 10 единиц одного числа приходится одна единица следующего числа.
- 10 единиц = 1 десяток;
- 10 десятков = 1 сотня;
- 10 сотен = 1 тысяча;
- 10 тысяч = 1 десяток тысяч;
- 10 десятков тысяч = 1 сотня тысяч;
- 10 сотен тысяч = 1 миллион.
Если одна сложная единица больше другой, она называется высшей дивизионной единицей. Если он меньше, его называют подразделением низшего дивизиона. Так, например, 100 единиц — это более высокая единица измерения расстояния по сравнению с 10 единицами, но более низкая по сравнению с 1000 единицами.
Многозначные числа. Единицы разрядов и классов. Сумма разрядных слагаемых.
В математике существует огромное количество натуральных чисел. Все по-разному. Примеры 2, 67, 354 и 1009. рассмотрим эти числа подробнее. Физическое число 2 состоит из одной цифры, поэтому такое число называется однозначным. Другой пример единичного числа: 3, 5, 8. Это число называется двузначным, потому что физическое число 67 состоит из двух цифр. Примеры двузначных чисел: 12, 35, 99. трехзначные числа состоят из трех цифр, например, 354, 444, 780. четырехзначные числа состоят из четырех цифр, например, 1009, 2600, 5732.
2-значный, 3-значный, 4-значный, 5-значный, 6-значный и т.д. Такие номера называются многозначными.
Разряды чисел.
Рассмотрим число 134. Каждая цифра этого числа имеет свое место. Эти места называются цифрами.
Цифра 4 занимает номер позиции или единицы измерения. Число 4 иногда называют первым числом. Число 3 занимает место или позицию 10. В качестве альтернативы цифра 3 может быть названа второй цифрой. Число 1 находится в порядке сотен. В качестве альтернативы цифра 1 может быть названа третьей цифрой. Число 1 является последней цифрой числа 134, поэтому число 1 называется старшей цифрой. Старший разряд всегда больше нуля.
Каждые 10 единиц любого разряда образуют новую единицу высшего разряда. Десять точек образуют класс десятков, десять десятков — класс десятков, сотни — класс сотен, а тысячи — класс тысяч. Если число отсутствует, оно заменяется нулем.
Например, число 208. Число 8 — это первая цифра единицы. Число 0 — это вторая цифра числа 10. Ноль не имеет математического значения. Список показывает, что десятки нет. Число 2 — это третья цифра сотни.
Такое деление числа называется цифровой конфигурацией числа.
Классы.
Многозначные числа делятся на группы из трех цифр справа налево. Эти группы цифр называются классами. Первый класс справа называется классом единиц, второй класс тысяч, третий класс миллионов, четвертый класс миллиардов, пятый класс, четвертый класс единиц, седьмой класс седьмых классов. Пять городов и седьмой класс.6-мм.
Классы единиц — Первый класс с правой стороны трех цифр, состоящий из цифр единиц, десятков и сотен. Порядок тысяч — второй класс состоит из отрезков тысяч, десятков и сотен тысяч. Порядок миллионов — третий класс состоит из чисел: миллионы единиц, десятки миллионов и сотни миллионов.
Рассмотрим пример: есть число 13.562.006.891. Это число имеет 891 единицу в категории единиц, 6 пунктов в категории категорий, 562 пункта в категории миллионов и 13 пунктов в категории миллиардов.
Таблица разрядов и классов.
Чтобы прочитать натуральное число 13562006891, количество единиц в каждом классе нужно читать слева направо, записывая три цифры класса 13 562 006 891 с правой стороны.
Главной особенностью этой серии считается бесконечность. Это связано с тем, что максимального числа не существует. У каждого компонента серии есть «старый партнер».
Разрядные слагаемые в математике

Число — это математическое понятие, которое также используется для количественного описания части или частей ряда, сравнения целого с его частями и расположения их по порядку. Значение числа представлено различными комбинациями символов или цифр. Сегодня цифры от 1 до 9 и 0 используются практически везде. Числа в виде семи латинских букв используются редко и здесь не рассматриваются.

В списке: «1, 2, 3 … 44» или непрерывная схема: «1-й, 2-й, 3-й … 44» используются натуральные числа, называемые натуральными числами. Все множество называется «рядом натуральных чисел», обозначаемым латинской буквой n. Всегда существует большее число и нет конца, так как нет больших чисел.
Разряды и классы чисел
Разряды
Таким образом, мы видим, что числовая мощность числа — это его позиция в файле чисел, и любое значение может быть выражено как nnn = n00 + n0 + n где n — число от 0 до 9.
Дюжина — это вторая единица, а 100 — третья цифра. Первая разрядная единица называется простой, а все остальные — составными.
Для облегчения записи и передачи цифры сгруппированы по трем категориям. Для удобства чтения между классами допускается взаимодействие.
Классы
Первая — максимальная трехзначная единица.
213 содержит следующие номера: 200, 110 и первые три единицы.
45 состоит из четырех десятков и первых пяти единиц. Второй — тысячи, от четырех до шести цифр.

Этот итог состоит из суммы следующего разряда.
- шестьсот тысяч,
- семьдесят тысяч,
- девять тысяч,
- восемьсот,
- десять,
- два,
- 3 456 = 3000 + 400 +50 +6.
За четвертой цифрой нет итога.

Третья — миллионы, 7-9 цифр.
Этот номер содержит девятизначный итог.
- 800 миллионов,
- 80 миллионов,
- 7 миллионов,
- 200 тысяч,
- 10 тысяч,
- 3 тысячи,
- 6 сотен,
- 4 десятка,
- 4 единицы,
- 7 891 234.
Это число не содержит итогов, превышающих седьмую цифру. Четвертый, миллиарды, от 10 до 12 цифр:.
567 млрд 892 млн 234 тыс. 976.
Цифры в категории 4 читаются слева направо.
- единицы сотен миллиардов,
- единицы десятков миллиардов,
- единицы миллиардов,
- сотен миллионов,
- десятков миллионов,
- миллионов,
- сотен тысяч,
- десятков тысяч,
- тысяч,
- простые сотни,
- простые десятки,
- простые единицы.
Цифры нумеруются, начиная с наименьшей и заканчивая наибольшей. Если в общем числе нет промежуточного значения, запись вводится с нулями, а название отсутствующей цифры и разряда единицы не произносится:.
4 000 миллиарда 4. Здесь не произносятся названия следующих посадок, потому что они отсутствуют: десятая и одиннадцатая четвертого класса, девятая, восьмая и седьмая третьего, десятая третьего, названия второго класса и их посадки не произносятся, а их сотни — десятки единиц.
Пятая — триллионы, тринадцать-пятнадцать цифр.
487 триллионов 799 миллиардов 665 миллионов 427 миллионов 441.
Запишите число 9 530 в виде суммы цифр. Это число включает 900 000, 5 000 единиц и 30 000. Поскольку три цифры больше нуля, это число содержит три цифры (900 000, 5 000 и 30).
Особенности разложения
Чтобы лучше понять цифровые компоненты и их использование в математике, стоит подробно рассмотреть процесс разложения натуральных величин на эти компоненты. В основе большинства проблем с суммами цифр лежит деление натуральных чисел, т.е. представление их в виде суммы цифр путем сложения количеств всех разрядных единиц.
Сложные натуральные числа, т.е. многозначные (например, двузначные, трехзначные и т.д.), могут быть преобразованы в суммы цифровых компонентов. Чтобы правильно разделить число на цифры, необходимо соблюдать основные правила. Во-первых, нули не учитываются при построении цифр числа. Во-вторых, добавки перечислены в порядке приоритета. То есть, сверху вниз, сначала тысячи, потом сотни, потом десятки. Последний вариант прост.
Состав чисел может быть описан тремя способами
- базовый — простое сложение: 852768 = 800 000 + 50 000 + 2000 + 700 + 60 + 8;
- подробный — сложение с умножением единиц разряда на их количество: 852768 = 8*100 000 + 5*10 000 + 2*1000 + 7*100 + 6*10 + 8*1.
- словесный — текстовая расшифровка: 852768 = восемь сотен тысяч, пять десятков тысяч, две тысячи, семь сотен, шесть десятков, восемь простых единиц.
Независимо от выбранного метода, разложить число на составляющие, исходя из его числового значения, не очень сложно. Конечно, чем больше число, тем выше риск путаницы и ошибок. Лучше всего начинать с двузначных чисел и постепенно увеличивать количество цифр.

Упражнения для тренировки
Стоит выполнить несколько упражнений, чтобы лучше понять материал. Некоторые примеры математических упражнений по этой теме:.
- 75 = 70 + 5;
- 324 = 300 + 20 + 4;
- 8434 = 8000 + 400 + 30 + 4;
- 68 486 = 60 000 + 8000 + 400 + 80 + 6;
- 575 783 = 500 000 + 70 000 + 5000 + 700 + 80 + 3;
- 8 633 087 = 8 000 000 + 600 000 + 30 000 + 3000 + 80 + 7.
Нередко упражнения выполняются в обратном порядке. То есть упражнения, в которых нужно найти количество его составляющих.

Стоит отметить, что не все проблемы с цифровыми данными решены. Многие упражнения включают в себя технику удаления. Однако эти проблемы трудно заметить только на первый взгляд. Их суть проста. В скобках указаны два числовых компонента: редукция и абстракция. Найдите их разность: (500 + 40 + 1) — (400 + 20) = (100 + 20 + 1) = 121.
Процесс деления чисел и прибавления обратного числа очень важен для решения различных математических задач и упражнений. Умение быстро анализировать числа любого размера в цифрах очень важно. Этот навык помогает при выполнении ментальной арифметики и многозначных функций.
Изучение физических чисел и оцифровки чисел является частью базовой учебной программы по математике. Этот материал преподается детям начальной школы.








