Эти знания можно легко применить к широкому кругу задач по геометрии. Часто требуется найти расстояние между точкой и прямой. Это расстояние можно определить, зная вектор направления линии. Предположим, что у нас есть следующие координаты: a- (x1; y1). Линия проходит через A(x2; y2). Точка задана Q(x0; y0).
Введение
Длина дуги большого круга — это кратчайшее расстояние между любыми двумя точками на поверхности сферы, измеренное вдоль линии, соединяющей эти две точки (такая линия называется ортогональной) и пересекающей поверхность сферы или другой вращающейся поверхности. .
Сферическая геометрия отличается от обычной евклидовой геометрии, и уравнение расстояния принимает другую форму. В евклидовой геометрии кратчайшее расстояние между двумя точками — это прямая линия. На сфере нет прямых линий. Эти линии на сфере являются частью большего круга. Центр окружности совпадает с центром сферы.
Начальный азимут — это азимут, полученный в начале движения из точки А. Кратчайшее расстояние до точки В проходит по длинной окружности и заканчивается в точке В. При движении из точки A в точку B по большому кругу. линии, угол азимута от текущего положения точки назначения B постоянно меняется. Начальный азимутальный угол отличается от фиксированного азимутального угла. При этом азимутальный угол от текущей точки до точки назначения остается неизменным, а путь не является кратчайшим расстоянием между двумя точками.
Если любые две точки на поверхности сферы не находятся точно напротив друг друга (т.е. не противоположны), можно нарисовать один большой круг. Две точки, большой круг делится на две дуги. Длина кратчайшей дуги — это кратчайшее расстояние между двумя точками. Между двумя антиподальными точками можно провести множество больших окружностей, но расстояние между ними одинаково для каждой окружности и равно половине окружности или π* R. где R — радиус сферы.
На плоскости (декартова система координат), как упоминалось выше, большой круг и его фрагменты являются дугами во всех проекциях, кроме геномов, где большой круг прямой. На практике это означает, что самолеты и другие авиалинии всегда используют короткие расстояния между пунктами для экономии топлива. Это означает, что полеты совершаются вдоль больших круговых расстояний, которые выглядят как дуги на плоскости.
Поскольку форму Земли можно описать как шар, уравнение для расчета расстояний по большому кругу важно для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используется в навигации.
Вычисление расстояний таким способом более эффективно и часто более точно, чем вычисление их по проецируемым координатам (в декартовых координатах), поскольку нет необходимости сначала преобразовывать географические координаты в декартову систему координат (в декартовых координатах). (например, в декартовой системе координат). проекции) и, во-вторых, многие проекции при неправильном выборе могут привести к искажениям значительной длины, что обусловлено определенными характеристиками проекционного искажения.
Известно, что эллипсоид, а не сфера более точно отображает форму Земли, но в этой статье описывается вычисление расстояний на сфере. В расчетах используется сфера с радиусом 6372795 метров, что может привести к ошибке расчета расстояния в 0,5%.
Формулы
Существует три способа вычисления сферического расстояния большого круга.
1. Сферическая теорема косинусов
Если расстояние небольшое, а количество цифр (десятичных знаков) мало, при использовании формул могут возникнуть серьезные ошибки из-за округления.
φ1, λ1; φ2, λ2 — широта и долгота двух точек в радиусе
Dl — разница между вертикальными координатами
Чтобы перевести угловые расстояния в метрические, разность углов нужно умножить на радиус Земли (6372795 метров). Конечная единица измерения расстояния равна единице, в которой выражен радиус (в данном случае метры).
2. Формула гаверсинусов
Это используется для того, чтобы избежать проблем на коротких расстояниях.
3. Модификация для антиподов
На предыдущее уравнение также влияет проблема антиподальной точки, которая решается с помощью следующей модификации.
В этой статье мы рассмотрим, как теоретически определить расстояние до точки и примеры конкретных задач. Сначала даются некоторые определения.
Как определить расстояние между точками, находящимися на координатной прямой
Чтобы найти расстояние от одной точки до другой, то есть длину данного отрезка, нужно сравнить его с другим таким же отрезком в определенном масштабе.
Рассмотрим этот метод на примере.
Вот линия с координатами OX, обозначенная точкой A. Поскольку это произвольное число, можно задать любое действительное число; допустим, 3.
Поскольку отрезок — это единица длины, все отрезки, которые нужно добавить из точки C, должны быть добавлены. Таким образом, результирующее количество сегментов равно длине сегмента OA. В этом случае ответ тот же, так как есть три части.
Другой пример, когда точка O и любая точка A соединены двумя частями. Это означает, что расстояние между всеми единичными отрезками OA равно 2. Если количество точек A разное (например, 6), то от точки O до искомого расстояния отделяется ровно 6 единичных отрезков.
Рациональные числа
С действительными числами все понятно, но как быть с рациональными числами? Предположим, что координаты точки A равны 5,5. Поэтому нам нужно получить отрезок в 5 единиц, или целое число, от точки O, а затем прибавить 0,5. Это может показаться невозможным, поскольку некоторые числовые значения трудно представить в виде линейных отрезков. Поэтому необходимо найти наиболее близкое значение к числовому значению.
Для неявных чисел этот метод не подходит, так как эти числа нельзя поместить на координатную линию OX. Например, рассмотрим числа √5, √8 и √17. Теперь мы можем перейти к абстрактному представлению и проверить эти числа следующим образом.
Можно сказать, что это относится и к действительным числам. Если точка A находится в начальной точке O, то расстояние между ними равно нулю. Геометрия должна хорошо поддаваться обработке. Тогда все становится ясно.
Важно помнить, что расстояние между точками не может быть отрицательным.

В данном случае существует коэффициент числа A, который является расстоянием OA и числа 3.
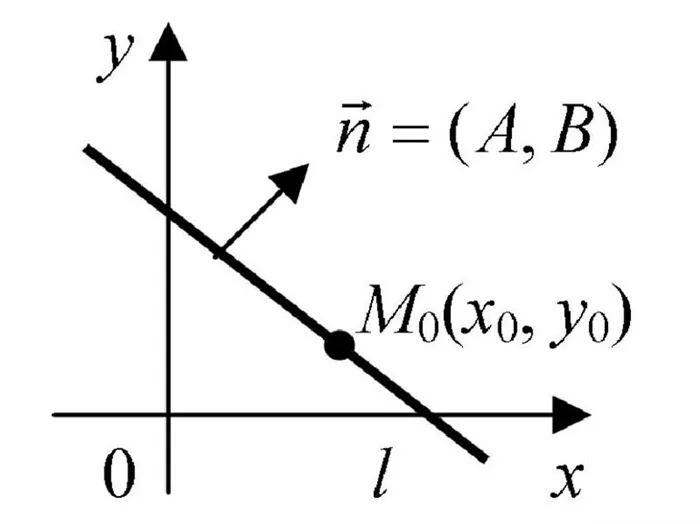
Если на координатной прямой есть точки A и B, то расстояние между ними должно быть определено путем измерения разности этих координат. Чтобы найти длину отрезка AB, нужно вычесть количество точек A из количества точек B.
Как определить расстояние между двумя точками на плоскости
Там находятся точки A и B, представляющие декартову систему координат и ее плоскость. Затем проведите линии от этих точек к осям Ox и Oy, как показано на рисунке. В результате образуются точки Ax и Ay и Bx и By.
Из этого можно сделать вывод о различных вариантах.
Если точки A и B лежат на прямой, перпендикулярной оси Ox, то точки A и B совпадают, а измеренное значение AB равно измеренному значению AyBy. Как упоминалось ранее, для нахождения длины промежутка (расстояния) между двумя точками требуется найти разность коэффициентов координатных данных, что можно выразить следующим образом.
При таком совпадении их расстояние равно нулю.
Уравнение для нахождения расстояния между двумя точками на плоскости:.
Теперь рассмотрим случай, когда линия перпендикулярна оси Oy. Расстояния одинаковые, но используются xB и xA. | AB | = | AxBx | = |xB-xA|.
Уравнение для нахождения расстояния между двумя точками на плоскости:.
Теперь поговорим о прямоугольном треугольнике ABC. Чтобы найти расстояние в плоскости между точками A и B, нужно воспользоваться следующим уравнением.
Это уравнение доказывает правильность написанного ранее утверждения о задаче, где на графике изображены точки, перпендикулярные Ox и Oy.
Если точки симметричны, то уравнение применяется следующим образом
AB | =√(xB-xA)²+(yB-yA)²=√0²+0²=0.
| AC | = | AxBx | и |BC| = |AyBy|. Далее вспомните теорему Пифагора и используйте ее для записи уравнений.
Если известно, что значения находятся в декартовой системе координат A (3, -1) и B (X + 3, 7), найдите расстояние между двумя точками на плоскости. Также найдите значение действительного числа X. Используя их, расстояние между точками равно 10.
Из школьных уроков геометрии мы знаем, что она понимается как дисциплина с определенной направленностью. Он символизируется в виде прямой линии конечной длины со стрелкой на конце.
Расстояние между точками на плоскости
A и B лежат на плоскости декартовой системы координат O x y, с заданными координатами A (x A, y A) и B (x B, y B).
Проведите перпендикулярные прямые через точки A и B на координатных осях Ox и Oy, чтобы получить проекции точек A x, A y и B x, By. Учитывая положение точек A и B, возможны следующие варианты.
-Если точки A и B совпадают, то расстояние между ними равно нулю.
-Если A и B лежат на прямой, перпендикулярной Ox (оси ребра), то A и B совпадают и | A B | = | A y B y |. Если расстояние между точками равно коэффициенту разности их координат, то A y B y = y B —y A, поэтому A B = A y B y = y B—yA.
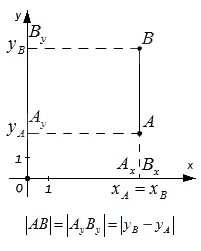
-Если A и B лежат на прямой, перпендикулярной оси Oy (ось под прямым углом) — пропорционально предыдущему коэффициенту: A B = A x B x = x B-x A
-Если точки A и B не перпендикулярны одной из координатных осей, найдите расстояние между ними и выведите формулу.
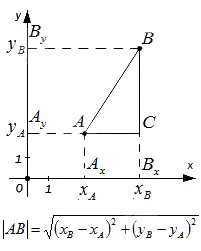
Мы видим, что треугольник ABC является прямоугольным по построению. Следовательно, A C = A xBx и BC = A yBy. Используя теорему Пифагора, составьте уравнение A B 2 = A C 2 +BC2 ⇔ AB2= A x B x 2 + A y B y 2 и преобразуйте его: A B = A x B x 2 + A y B y 2 = x B-x A 2 + y B-y A 2 = (x B-x A)2 + (y B-y A)2
Сделайте выводы из этого результата. Расстояние от точки A до точки B на плоскости определяется уравнением с использованием координат этих точек
A B = (x B-x A)2 + (y B-y A)2
Эта формула также доказывает предыдущую формулу, если точки совпадают или если точки лежат на прямой, перпендикулярной оси. Таким образом, если точки A и B совпадают, то применимо следующее уравнение A B = (x B-x A)2 + (y B-y A)2 = 0 2 + 0 2 = 0
Если точки A и B прямые и перпендикулярны оси дивергенции:.
a b = (x b -x a)2 + (y b -y a)2 = 0 2 + (y b -y a)2 = y b -y a
Если точки a и b лежат на прямой вертикали на оси легитимности
a b = (x b -x a)2 + (y b -y a)2 = (x b -x a)2 + 0 2 = x b -x a
Расстояние между точками в пространстве
Исходные данные: прямоугольная система координат O X Y Z с произвольными точками, заданными координатами A (X A, Y A, Z A) и B (X B, Y B, Z B); необходимо определить расстояние между этими точками.
Рассмотрим общий случай, когда A и B не находятся на уровне, параллельном одному из уровней координат. Проведите вертикальный перпендикуляр к оси через точки A и B относительно координатных осей и получите соответствующие точки обзора: a x, a, a z, b x, b y, b z
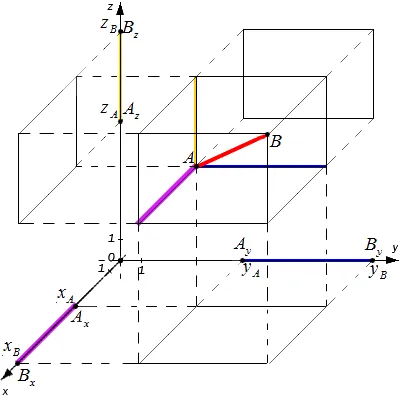
Расстояние между точками A и B является результирующей косой. Согласно этой параллельной пиратской конструкции, A x b x, a y b y, z b z
Из курса геометрии известно, что квадраты параллельных диагоналей равны сумме квадратов этой размерности. Этот тип дает равенство: a b 2 = a x b x 2 + a y b y 2 + a z b z 2
Используя предыдущие выводы, напишите
a x b x = x b -x a, a y b y = y b -y a, a z b z = z b -z a
a b 2 = a x b x 2 + a y b y 2 + a z b z 2 = x 2 = x a 2 + y b -y a 2 + z b -z a 2 = (x b -x a) 2 + (y b -y a) 2 + z b -z a 2
Окончательный вид, определяющий расстояние между двумя точками в пространстве, имеет вид
a b = x b -x a 2 + y b -y a 2 + (z b -z a)2
Этот тип также относится к случаям
— Они находятся на прямых линиях, параллельных одной координатной оси или одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Задана прямая с заданными координатами A (1-2) и B (11 + 2) и ее точки. Найдите расстояние от начала до a и между a и B
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно O A = 1 — 2 = 2 — 1
- Расстояние между точками A и B определим как модуль разности координат этих точек: A B = 11 + 2 — ( 1 — 2 ) = 10 + 2 2
Ответы: o a = 2-1, a b = 10 + 2 2 2
Исходные данные: дана прямоугольная система координат и две точки (1, -1) и B (λ + 1, 3) в ней. λ — действительное число. Вам нужно найти все значения этого числа, для которых расстояние A равно 5.
Чтобы найти расстояние между a и b, используйте вид a b = (x b -x a)2 + y b -y a 2
Заменив действительные значения координат, получаем b = (λ + 1-1)2 + (3-(- 1))2 = λ2 + 16
Кроме того, для использования условия a b = 5 применяется следующее уравнение
λ2 + 16 = 5 L 2 + 16 =25λ=±3
Дано трехмерное пространство в прямоугольной системе координат O X Y z, указывающее на A (1, 2, 3) и b -7, -2, 4.
Для решения задачи используйте тип A b = x b -x a 2 + y b -y a 2 + (z b -z a)2
Заменив фактические значения, получаем b = ( — 7-1)2 + ( — 2-2)2 + (4-3)2 = 81 = 9
В трехмерном пространстве евклидово расстояние между двумя точками p и q с координатами (x₁, y₁, z₁) и (x₂, y₂, z₂) определяется как
Характеристики объекта
Как и другие геометрические объекты, векторы обладают набором математических свойств, которые используются для решения задач. Основные из них следующие.
- a- и b- можно складывать и вычитать, при этом получаются новые вектора;
- вектора a- и b- можно умножать друг на друга, существует возможность выполнить скалярное или векторное умножение, каждый вид операции имеет свой геометрический смысл;
- объект однозначно определяется всего двумя точками независимо от мерности пространства;
- он имеет модуль, который геометрически представляет длину его отрезка.
Для всех качеств существуют правила, которые их определяют. Например, при удалении вектора a- из B-, ребра этих объектов должны быть соединены с отрезком и в направлении конца a-. Это приведет к вектору конфликта.
Умножение векторов A и B — полезная операция для определения площади и объема фигуры. Для этого необходимо знать, как работать с квадратичными и кубическими таблицами, в частности, как вычислять определители.
Универсальный способ
Это представление координат геометрических фигур в нулевом, одном, двух и трех измерениях. Параметры точек, треугольников, квадратов, линий, плоскостей и других более сложных объектов могут быть однозначно представлены в виде набора чисел, связанных с соответствующей системой координат. В связи с проблемой использования координат для определения расстояний от точки до точки, имеет смысл рассматривать только данный конкретный одномерный объект и вектор.
Точка на плоскости
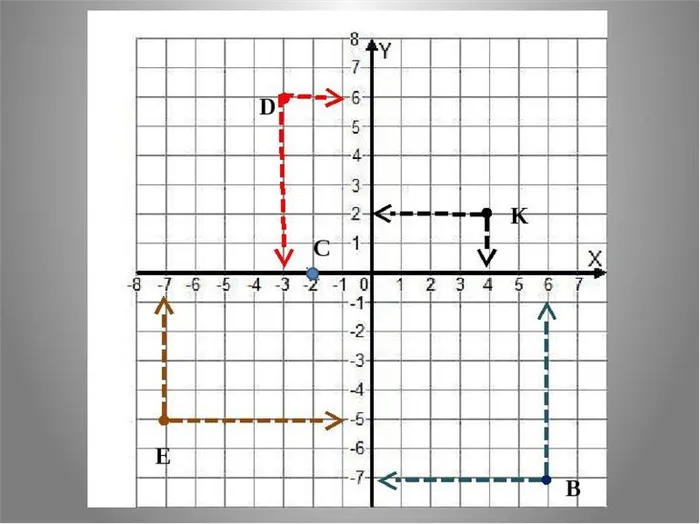
Этот объект является нульмерным. Чтобы определить его однозначно, достаточно знать только набор чисел, связанных с системой координат. Поскольку на плоскости есть только две вертикальные оси x и y, каждая точка имеет две координаты. Например, A (3; 2), B (-1; 4), C (0; -2), D (0; 0). Первое число здесь означает количество отрезков, разрезанных по оси x, второе — по оси y. Точка D находится в начальной точке координат, т.е. на пересечении x и y.
В общем случае удобно определить произвольную точку Q (x0; y0).
Направленный отрезок в двумерном пространстве
На плоскости координаты отрезка прямой, например, точки, представляют собой два набора чисел. Оба указывают количество сегментов единичной длины, которые необходимо разместить по каждой оси для создания вида вектора по осям x и y. Например, данные a- (1; -2) означают, что для получения a- необходимо отложить отрезок 1 * i- на оси x и -2 * j- на оси y (2 единицы j- в отрицательном направлении оси y. Пересечение этих проекций является концом a-. Его начало — (0; 0).
В плоском и трехмерном пространстве только две точки однозначно определяют направленный отрезок. Если его начало перенести на пересечение осей x и y, то его конец можно легко найти, вычтя соответствующие координаты точки между ними. Следующий простой пример иллюстрирует вышесказанное
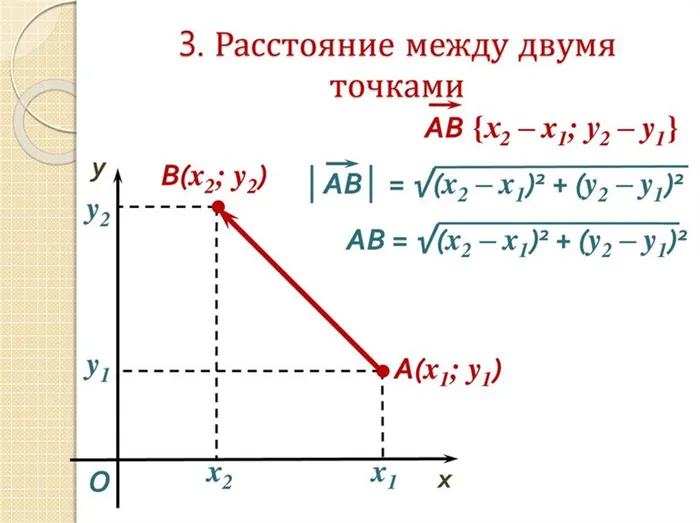
Даны точки A (x1; y1) и B (x2; y2), AB- имеет следующие координаты
Вторая точка указывает на положение конца AB-.
Формула дистанции
С полученными знаниями и знаниями о свойствах точек и векторов можно перейти к вопросу нахождения вида расстояния. Согласно геометрическому определению, расстояние между двумя точками понимается как длина отрезка, соединяющего их. Это значение также равно модулю вектора, построенного из нулевого объекта.
Длину направленного отрезка на плоскости можно легко определить. Каждую координату необходимо возвести в квадрат и сложить полученные значения, чтобы получить квадратный корень из полученной суммы. Для вектора a- (x; y) длина равна
Увеличение суммы до степени 0,5 эквивалентно извлечению ее квадратного корня.
Поскольку определение координат вектора по соответствующим значениям точек известно, можно получить следующие простые уравнения для A(x1; y1) и B(x2; y2).
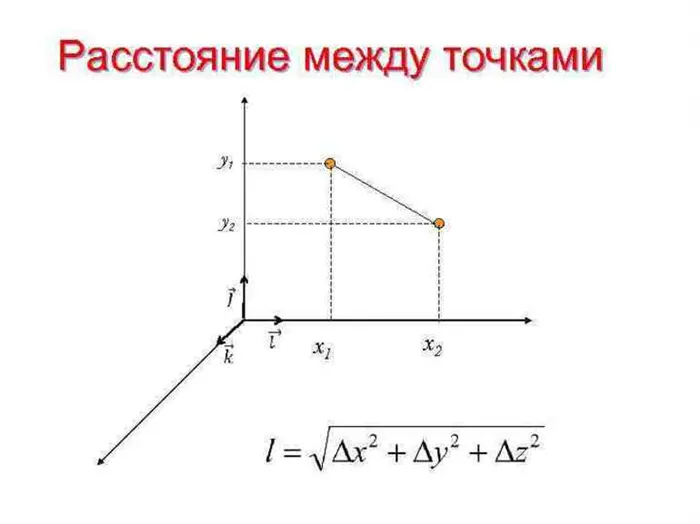
В трехмерном пространстве соответствующие уравнения имеют аналогичный вид, за исключением того, что добавляется третья z-координата.








