Термин имеет латинский корень — «ratio» означает «число», «расчет», «причина», «рассуждение» или «нумерация». Но есть и другие переводы — «дробь» и «деление».
Как решать рациональные числа
Разумное число (лат. разум, деление, дробь) — это число, обычно выраженное в виде пропорции » /> и натурального числа, например, ¼. Вещи (длина, вес, площадь и т.д.), они поняли, что целые числа невозможны и необходимо ввести понятие дробей: половинки, трети и т.д., использовались дроби и дробные части и их действия. шумерами, древними египтянами и греками.
Разумный набор чисел может быть показан и описан в следующем виде
\ mid m \ в \ mathbb, n \ в \ mathbb \ right \>. » />
Видно, что разные записи могут представлять одну и ту же фракцию. » /> и » />, (все дроби, которые могут возникнуть вместе при умножении или делении одного и того же натурального числа, представляют одно и то же рациональное число). Разделив числитель и знаменатель на наибольший общий делитель, можно получить единственное представление рационального числа без балльной оценки.
\ mid m \ in \ mathbb, n \ in \ mathbb, ⌘ gcd(m, n) = 1 \ right \>. » />
Здесь и
Множество логических чисел является естественным обобщением всех целых чисел. Если у рациональных чисел знаменатель является целым числом, то множество рациональных чисел является плотным на всей оси чисел. Тем не менее, мы обнаружили, что все рациональные числа измеримы (т.е. все их элементы могут быть отброшены). Заметим, кстати, что древние греки были убеждены в существовании чисел, которые невозможно выразить как дроби (например, они показали, что не существует рационального числа, квадрат которого равен 2).
Терминология
Формальное определение
Обычно рациональные числа определяются в терминах эквивалентности как множество классов эквивалентности ЈRight Ј> » />.
Связанные определения
Правильные, неправильные и смешанные дроби
Дробь — это дробь, мера числителя которой меньше меры знаменателя. Правильная дробь — это рациональное число по модулю. Дроби, которые не являются обычными дробями, называются неправильными дробями и представляют собой разумное число одного или нескольких модулей.
Неправильная дробь может быть выражена как сумма целого числа и обычной дроби, которая называется смешанной дробью. Например, = 2 + \ frac = \ frac + \ frac = \ frac»/>. Этот шрифт (с опущенными дополнительными знаками) используется в элементарной арифметике, но избегается в строгой математической литературе из-за сходства написания. Дроби и фрагменты произведения целых чисел смешиваются.
Высота дроби
Высота дроби равна сумме коэффициентов числителя и знаменателя дроби. Высота рационального числа равна сумме коэффициентов числителя и знаменателя несократимой дроби, соответствующей этому числу.
Например, высота дроби » /> равна , так как дробь сокращается на
Комментарий
Термин дробное число (дробь) иногда определяется как синоним термина логическое число, а иногда как синоним нецелого числа. В последнем случае дроби и рациональные числа различны. Это связано с тем, что нецелые рациональные числа являются лишь частным случаем дробных чисел.
Свойства
Основные свойства
Множество рациональных чисел удовлетворяет 16 основным свойствам, которые можно легко извлечь из свойств целых чисел. 1


Дополнительные свойства
Все остальные свойства рациональных чисел обычно не считаются фундаментальными, поскольку они не основаны на свойствах целых чисел и поэтому могут быть доказаны с помощью определения фундаментальных свойств или математических объектов. Существует множество таких дополнительных свойств. Целесообразно привести здесь лишь некоторые из них.
Числа, записанные в такой форме, называются смешанными числами. Она состоит из двух частей: целой и дробной. Таким образом, для каждой неправильной дроби ее можно записать как смешанное число (или как натуральное число). Обратное также применимо. Смешанные или натуральные числа могут быть записаны в виде неправильных дробей. Например.
Отличие между целыми, натуральными и рациональными числами
Натуральные числа — это числа, используемые при счете: 1,2,3,4,5 … 100 … И т.д. Наименьшее натуральное число равно 1, а наибольшее физическое число не существует. Они используются для измерения чего-то конкретного, например, 2 кошки, 5 лошадей, 20 стульев и т.д.
Целые числа — это натуральные числа + противоположные числа + ноль. Если два числа отличаются на один символ, они называются противоположными числами. Например, +2 и -2, +7 и -7. знак плюс обычно не пишется. Если числу не предшествует символ, оно означает положительное значение. Числа, которым предшествует символ минус, называются отрицательными числами.
Рациональные числа — это целые числа + дроби (обычно десятичные, журнальные). Каждое рациональное число может быть выражено в виде дроби. Здесь ➜ числитель — целое число, а ➜ знаменатель — натуральное число.
Однако не все числа можно назвать рациональными. Примерами чисел, которые не являются рациональными числами, являются: — бесконечные непериодические дроби; — корни из числа, которые дают бесконечные непериодические дроби (√3); — 𝜋 (число π).
Обратные числа
Обратное число — это число, которое получается при умножении данного числа. Например, число и 1/5 взаимно обратны, так как произведение равно единице. Нулевые числа не имеют обратной величины, потому что их нельзя разделить на ноль.
Противоположные числа — это два числа, знаки которых отличаются друг от друга. Каждое разумное число имеет противоположное число. Числа в линейных координатах и одно противоположное число являются симметричными с точки зрения принципа. Другими словами, оба числа относятся к началу.
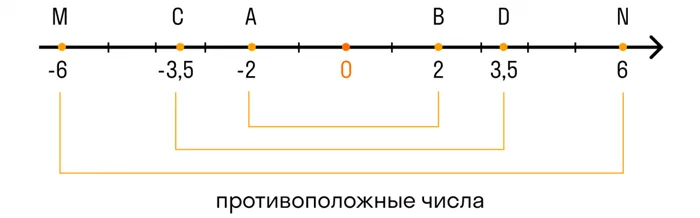
Модуль числа
Коэффициент числа — это расстояние от начала координатной прямой, соответствующей этому числу, до точки. Символика:| a |. Если взять число «a» и отметить его линейно с точкой A, то коэффициент числа «a» — это расстояние от начала (нуля) до точки a.
- модуль положительного числа — само число,
- модулем отрицательного числа — противоположное ему число,
- модуль ноля — ноль.
Рабочий должен был производить 80 компонентов за смену. В конце рабочего дня он отработал 150% от отведенной ему смены. Сколько аксессуаров изготовил работник?
Отрицательное значение перед рациональным числом
Рассмотрим простой пример:.
В данном примере делитель равен (-6), то есть отрицательный.
Затем вы можете рассмотреть другой пример. Составьте и запишите выражение.
В данном примере отрицательное число — это несводимое число, равное (-2). Однако в обоих случаях, решая пример, ответ один и тот же. То есть, (-3). Эти примеры также можно записать в виде дробных значений.
Форма этих значений ⌘frac= -3, -⌘ frac =-3⌘.
В обоих случаях перед суммой можно поставить отрицательный знак числителя или знаменателя, так как ответы, полученные при вычислении дробей, равны. Поэтому он располагается перед дробью.
Таким образом, поскольку дроби ɑ frac и ɑ-ɑ frac имеют одинаковое значение, их можно сделать равными ɑ frac = ɑ \ frac =-ɑ fracɑ.
Противоположные значения рациональных чисел
По аналогии с простыми числами, логические числа могут быть противоположными числами.
Например: если логическое дробное число равно ﷺ frac \, то обратным числом будет дробное число ﷺ -ﷺ fracﷺ.
Эта дробь располагается асимметрично на координатной прямой относительно дроби ⌘frac⌘ и начала. Это означает, что обе дроби находятся на одинаковом расстоянии от нулевого значения (начала).
Следующая диаграмма иллюстрирует это более подробно.

Основы перевода смешанных числовых значений в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь, умножьте целую дробь на дробный знаменатель и прибавьте полученное значение к дробному числителю.
Полученное вычисление становится числителем нового дробного числа. Таким образом, знаменатель остается неизменным.
Пример 1.\2 Вам нужно преобразовать смешанное число, равное \frac\, в неправильную дробь. Для этого умножьте целую часть на значение дробного знаменателя. Затем добавьте полученное значение к десятичному счетчику.
Определим значение выражения:.
(2 x 2) + 1 = 4 + 1 = 5 Вычисленное значение 5 является числителем нового дробного значения.
Десятичное значение. Значение знаменателя остается прежним ⌘frac⌘ Весь расчет можно записать в следующем уравнении: (2 x 2 + 1 = 4 + 1 = 5)⌘frac⌘ Значение знаменателя остается прежним.
Чтобы вернуться к первоначальной форме, вам необходимо заявить
В целом дробь frac есть Ј frac = 2 Ј \frac\.
Этот метод преобразования смешанных значений в неправильную дробную форму применяется, когда смешанное число является положительным значением. Для отрицательных чисел этот метод не подходит.
Для этого рассмотрим следующие дроби: ⌘-⌘frac\. Определите и разделите целые дроби, чтобы получить
Чтобы преобразовать дробь в исходную форму \-\frac\, нужно преобразовать смешанное число, равное \ -2 \frac\ в неправильную дробь.
Однако, если используется предыдущее правило. Для этого нужно умножить целую часть на цифры дробного знаменателя и прибавить к результату дробный числитель, но при этом возникает несоответствие.
Вычисляя данные, ответ ⌘-⌘ frac \, а правильный ответ должен быть ⌘-⌘ frac.
Видно, что значение смешанного числа ⌘-⌘frac⌘ было неправильно преобразовано в неправильную дробь.
Правильное решение требует преобразования отрицательного числа в неправильную дробь.
Для этого умножьте целое значение на дробь числителя.
Это решение является верным, и ответ будет правильным.

Пример 2. Вам нужно извлечь целую часть значения неправильной дроби Ј-ЈfracЈ. Преобразуйте полученное количество брутто-величин в неправильные дроби.
Используя известные методы и правила, экспортируйте всю деталь в заданное значение дроби\-{frac\}. Для данной дроби это выглядит так: Ј-Ј frac = -5 \ frac \
Далее необходимо преобразовать действие смешанного числа Ϯ -5 \frac \frac \frac \frac} в неправильные дроби.
Для этого умножьте всю дробную часть на знаменатель. Удалите дробную часть из полученного значения.
Для этого смешанное число заключают в скобки, а отрицательный знак помещают за скобками. Далее используйте уже известные правила конвертации. Умножьте значение интеграла на знаменатель дроби. Затем прибавьте числитель к полученному результату.
Объявление количества рациональных чисел может вызвать некоторую путаницу. Это связано с тем, что на первый взгляд создается впечатление, что оно гораздо шире, чем все натуральные числа. На самом деле это не так, и существует несколько натуральных чисел для подсчета всех рациональных чисел.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеокурсам, необходимо приобрести их в списке и добавить в личный кабинет.


Конспект урока «Свойства действий с рациональными числами»
Как вы уже знаете, все известные нам цифры разумны.
Вы можете складывать, вычитать, умножать и делить рациональные числа.
Мы также знаем, что удаление можно заменить умножением, сложением и делением. Это оставляет только два действия: сложение и умножение.
Сегодня, на этом уроке, мы рассмотрим свойства разумного числа действий и примем знания на конкретных примерах.
Мы рассмотрим дополнительные объекты недвижимости.
Дополнительные транснациональные и комбинаторные свойства применимы к каждому числу, а также к неотрицательным числам.

В примерах можно объединить дополнительные комбинаторные и постдополнительные свойства. Вы увидите, что дополнения можно выполнять в любом порядке.
Найдите значение выражения.
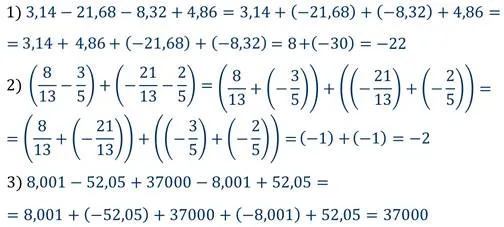
Давайте теперь рассмотрим свойства умножения.
Свойства умножения для неотрицательных чисел также применимы к каждому разумному числу. Наряду с распространением и сложением существуют свойства счетчика и комбинаторики.

Мачтовые и комбинационные свойства распространения позволяют переставлять и группировать множители, упрощая представление.
Распространение рациональных чисел имеет распределительные свойства умножения, связанные со сложением.
Для рациональных чисел b c применяются следующие уравнения.: .
Чтобы умножить сумму на число, сначала умножьте первое слагаемое на это число, затем умножьте второе слагаемое на это число, после чего сложите результат.
Распределительное свойство умножения также применимо.
Такое преобразование уравнения называется установкой общих множителей вне скобки.
Рассмотренные в данном курсе свойства акта с разумными значениями позволяют упростить расчет. Это значительно сокращает время, необходимое для выполнения задания, и позволяет избежать ошибок.
Этот метод преобразования смешанных значений в неправильную дробную форму применяется, когда смешанное число является положительным значением. Для отрицательных чисел этот метод не подходит.
Свойства рациональных чисел
Рациональные числа подчиняются всем основным законам математики.
- А + В = В + А
- А + (В + С) = (А + В) + С
- А + 0 = А
- А + (-А) = 0
- А * В = В * А
- А * 1 = А
- А * 0 = 0
- (А + В) * С = А * С + В * С
- (А – В) * С = А * С – В * С
Для интереса можно заменить буквы цифрами, чтобы узнать, применимы ли эти законы.
Чтобы сложить отрицательное рациональное число, добавьте числитель и минус перед ответом. Пример: (-10) + (-30) 1. Сложите модуль числа: 30 + 10 = 40 2. Добавьте минус перед ответом, чтобы получить -40.
Число
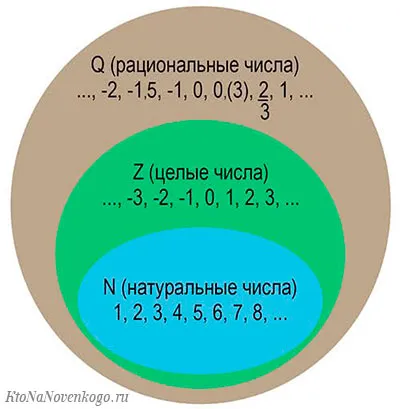
Число — это количество цифр, записанных в определенном порядке. Числа бесконечны, но есть только десять цифр от 0 до 9. Это целое, разделенное на несколько подмножеств. Во-первых, деление происходит между действительными и комплексными числами.
Во всех уравнениях, если невозможно найти корень числа, ответ записывается: корня действительного числа не существует. Это означает, что корень лежит между комплексными числами.
Комплексные числа редко используются в школах, а вот действительные числа используются широко.
Логическое число — это любое число, которое не содержит корня или корней. Рациональные числа — это: количество рациональных чисел, т.е. количество рациональных единиц в числе.
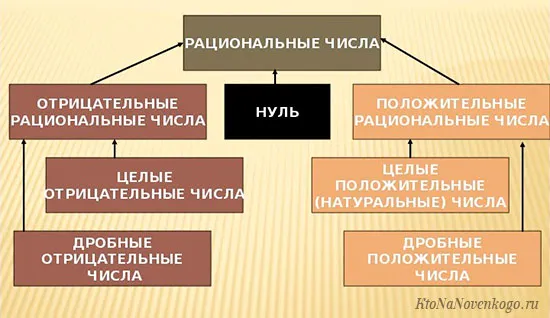
- Натуральные числа. То есть все числа от 1 и далее. Все эти значения используются для обычного счета, поэтому и называются натуральными. В эту подгруппу не входят отрицательные числа и дроби.
- Целые. Целыми числами зовутся положительные, отрицательные значения и ноль. Дроби сюда не относятся, именно по этой причине подгруппа и имеет такое название.
- Рациональные. Помимо целых и натуральных чисел в подмножество рациональных чисел входят и дроби. Они не относятся к натуральным или целым группам, поэтому считаются просто рациональными числами.
Очень часто студенты путаются, называя рациональные числа только дробями. На самом деле, натуральные и целые числа также можно рассматривать как примеры рациональных чисел. Эти два подмножества не должны быть опущены. Это может привести к ошибкам. Помните, что рациональное число — это любое число, которое не содержит знака корня.
Иррациональные числа
Вопрос в том, почему нельзя путать понятия рациональных и иррациональных чисел. Причина в том, что неявные числа подчиняются совсем другим законам. Ниже приведен пример.
Как происходит сложение логических чисел?
5 + 3 = 8 — это просто. Сложение дробей немного сложнее, но все же стоит хоть раз задуматься, и все сразу становится понятно. Но как решить такой пример?
$ \ sqrt + \sqrt$- не может быть выполнено. В нелепом примере такое выражение уже считается ответом. Если в задаче требуется найти ответ в вещественных числах, используется калькулятор. Само собой разумеется, точное число найти невозможно, и ответ приходится округлять в большую сторону.
Поэтому этот подход следует оставить на потом. В противном случае округление может сильно повлиять на окончательный ответ.








