Прямоугольный параллелепипед. Что такое прямоугольный параллелепипед

Полуэпителий с параллельными смежными поверхностями, образующими двойной угол.

Прямоугольный параллелепипед

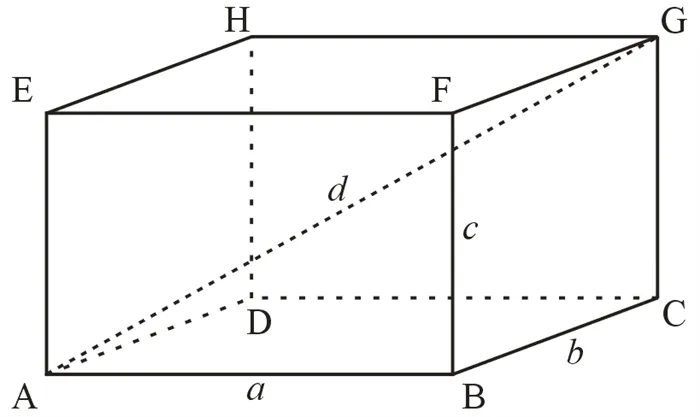
Прямоугольные прямоугольники — это объемные фигуры с шестью сторонами, каждая из которых прямоугольная.

Прямоугольные прямоугольники — это прямоугольные параллельные лепестки с прямоугольными краями.

Примерами прямоугольных параллелей являются классные комнаты, кирпичи и спичечные коробки.

Длины трех граней прямоугольного параллельного уровня с общим краем называются его размерами. Например, существуют спичечные коробки 15, 35 и 50 мм. Тип для нахождения прямоугольных параллельных объемов: v = abc

Прямоугольное параллельное ле с равными размерами называется кубом. Все шесть сторон куба — равные квадраты.

Квадраты длины диагонали прямоугольной параллели равны сумме квадратов ее трех измерений.

Ссылки

Фонд Викимедиа. 2010.

Параллелепипед — (от греч. parallel и греч. level) призма, основание которой … Википедия.

ENVIRONMENTAL PALEPELLIPPE -3.12 ENVIRONMENTAL PALEPELPE (frame of reference): воображаемая поверхность, представляющая собой наименьший прямоугольник, содержащий весь тест, в дополнение к выступающим частям с незначительными … …

Эйлерова параллель — рациональный кубоид (или целочисленный кирпич) — это прямоугольный параллельный лель, в котором семь главных измерений (три грани, три диагонали фасада, диагонали в пространстве) — все целые числа. Другими словами, рациональный куб … … Википедия.

Целевой параллелипп — это воображаемый прямоугольник, в котором, помимо незатронутых частей, находится полный источник шума, основанный на российском мини-круге по безопасности и охране труда.

Геометрия — это раздел математики, который занимается изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и связанных с ними положений. Для облегчения преподавания геометрия подразделяется на планетарную и стереометрическую. … …. Энциклопедия Кольера.

Тетраэдр — (греч. tetrahedron тетраэдр) Простейший многогранник, гранями которого являются четыре треугольника. Тетраэдр имеет четыре поверхности, четыре вершины и шесть граней. Содержание 1 Связанные определения … Википедия.

Равносторонний тетраэдр — Тетраэдр называется равносторонним треугольником, если все его грани являются треугольниками. Существует несколько эквивалентных определений: параллельный релипидаль, описываемый своим периметром, является прямоугольником — его печать состоит из трех срезов …

Рациональный кубоид — Рациональный кубоид (или интегральный кирпич) — это прямоугольный параллельный лель, в котором все семь главных измерений (три ребра, три диагонали и диагональное пространство) являются интегральными числами. Другими словами, рациональный куб … … Википедия.

Рациональный кирпич — Рациональный кубоид (или целочисленный кирпич) — это прямоугольный параллельный лель, семь главных измерений которого (три ребра, три диагонали и пространственная диагональ) являются целыми числами. Другими словами, рациональный куб … … Википедия.

Интегральный кирпич — Рациональный кубоид1 (или целочисленный кирпич) — это прямоугольный параллельный лель, в котором все семь основных измерений (три ребра, три диагонали и диагональное пространство) являются целыми числами. Другими словами, рациональный куб … … Википедия

Для ПП верно, что его объем равен цене тройного произведения трех векторов, исходящих из одной вершины. Тип ПП:.

Параллелепипед, сввойства прямоугольного параллелепипеда

Геометрия, образованная двумя равными параллелограммами на параллельных уровнях и их вершинами, соединенными с двумя парами прямоугольников на параллельных уровнях между параллельными уровнями, называется параллелепипедом (Рисунок 1).

Параллелограммы, составляющие параллельное расщепление, называются параллельными сторонами, стороны прямоугольников — параллельными сторонами, а вершины в одинаковых точках — параллельными вершинами.

Свойства параллелепипеда

Противоположные поверхности параллельных уровней равны и параллельны.

ЭВИДЕНЦИЯ.

Противоположные параллели возникают непосредственно из Определения 1.

Докажем равенство противоположных сторон. Для этого рассмотрим рисунок 2.

Рассмотрим грани

Легко запомнить все приведенные свойства. Они легко понимаются и логически вытекают из видов и свойств геометрических тел. Однако простые утверждения могут быть очень полезны при решении вопросов, связанных с использованием стандартов, и могут сэкономить время, необходимое для прохождения теста.

Параллелепипед, сввойства прямоугольного параллелепипеда

Геометрия, образованная двумя равными параллелограммами на параллельных уровнях и их вершинами, соединенными с двумя парами прямоугольников на параллельных уровнях между параллельными уровнями, называется параллелепипедом (Рисунок 1).

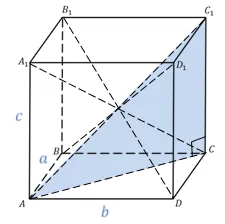
Параллелограммы, составляющие параллельное расщепление, называются параллельными сторонами, стороны прямоугольников — параллельными сторонами, а вершины в одинаковых точках — параллельными вершинами.

Прямоугольный параллелепипед

Можно выделить два конкретных случая применения параллельной концепции. Одним из них является понятие прямоугольных параллелей.

Прямоугольник, основание которого и все углы двух его углов равны, называется прямоугольником (рис. 4).

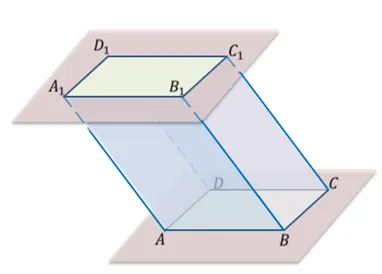
Рисунок 4: Настройка прямоугольной параллели

Прямоугольные прямоугольники имеют те же свойства, что и любые другие, но также обладают индивидуальными свойствами.

Сумма квадратов в трех измерениях (высота, длина и ширина) равна квадрату их диагоналей.

Математика Это можно записать так:.

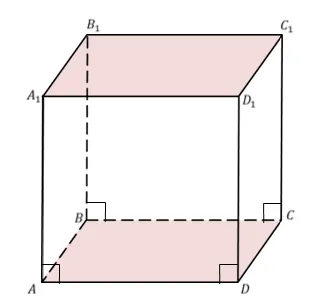
ЭВИДЕНЦИЯ.

Рассмотрим рисунок 5. Докажите это, например.

Рассмотрим треугольник $ adc $. Из теоремы Пифагора следует.

Поскольку $ abcd $ — прямоугольный треугольник, $ dc = ab $.

Рассмотрим треугольник $ acc_1 $. Из теоремы Пифагора следует, что

Прямоугольник с квадратной поверхностью — это куб (рис. 6).

1B_1B$ и

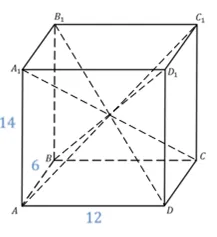
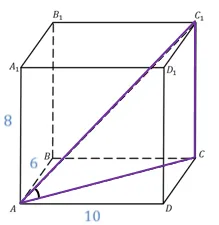
Проблема. Размеры параллельных уровней задаются точками, которые являются параллельными линиями, рассекающими прямоугольник, изображенный на рис. К краю точечного примечания.

Параллелепипед, свойства прямоугольного параллелепипеда

Геометрия, образованная двумя равными параллелограммами на параллельных уровнях и их вершинами, соединенными с двумя парами прямоугольников на параллельных уровнях между параллельными уровнями, называется параллелепипедом (Рисунок 1).

Параллелограммы, составляющие параллельное расщепление, называются параллельными сторонами, стороны прямоугольников — параллельными сторонами, а вершины в одинаковых точках — параллельными вершинами.

1C_1C$. Так как, по определению 1, грани параллелепипеда — параллелограммы, то

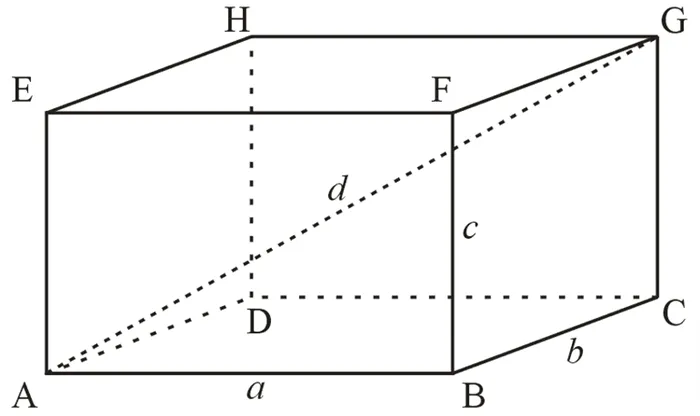
Одна из вершин основания (F) равноудалена от всех вершин нижнего основания параллелепипеда. Вместе с нижней диагональю (AC) они образуют равнобедренный треугольник ∆AFC. AF = AC по договору. AF — край фигуры.

Параллелепипед, свойства прямоугольного параллелепипеда

Геометрия, образованная двумя равными параллелограммами на параллельных уровнях и их вершинами, соединенными с двумя парами прямоугольников на параллельных уровнях между параллельными уровнями, называется параллелепипедом (Рисунок 1).

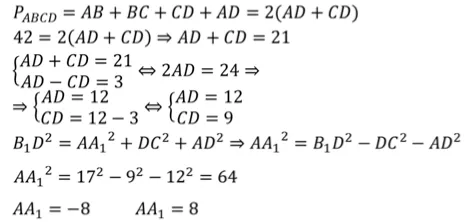
Параллелограммы, составляющие параллельное расщепление, называются параллельными сторонами, стороны прямоугольников — параллельными сторонами, а вершины в одинаковых точках — параллельными вершинами.

1=_1$ и $AB=DC.$ Так же

Рациональный кубоид — Рациональный кубоид (или интегральный кирпич) — это прямоугольный параллельный лель, в котором все семь главных измерений (три ребра, три диагонали и диагональное пространство) являются интегральными числами. Другими словами, рациональный куб … … Википедия.

Параллелепипед, свойства прямоугольного параллелепипеда

Геометрия, образованная двумя равными параллелограммами на параллельных уровнях и их вершинами, соединенными с двумя парами прямоугольников на параллельных уровнях между параллельными уровнями, называется параллелепипедом (Рисунок 1).

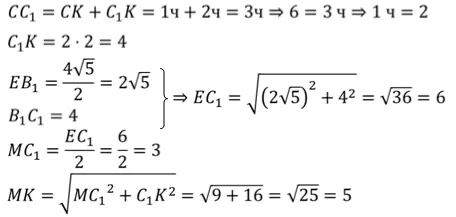
Параллелограммы, составляющие параллельное расщепление, называются параллельными сторонами, стороны прямоугольников — параллельными сторонами, а вершины в одинаковых точках — параллельными вершинами.

1||_1$ и $AB||DC$, следовательно, $\overrightarrow<_1>\ вверх по стрелке \ вверх по стрелке \ прямо по стрелке<_1>и $\overrightarrow \ uparrow \ uparrow \ overrightarrow $, т.е. $\ угол A_1AB = \ уголD_1DC$. Таким образом, согласно принципу равенства треугольников, $I$\треугольник A_1AB = ⌘треугольник D_1DC$. Аналогично, видно, что $\треугольник D_1C_1C =\треугольник A_1B_1B$. Таким образом, $D_1C_1CD =A_1B_1BA$. Аналогично доказывается эквивалентность других противоположных сторон.

Готовые работы на аналогичную тему

Теорема доказана.

Диагонали параллелограмма пересекаются в определенной точке и делятся в этой точке посередине.

ЭВИДЕНЦИЯ.

Докажем вначале, что диагонали $A_1C$ и $D_1B$ делятся точкой пересечения $O$ пополам. По теореме 1, имеем $A_1D_1=BC$ и $A_1D_1||BC$. Следовательно, $A_1D_1CB$ — параллелограмм. Тогда, по свойству параллелограмма, получим, что диагонали $A_1C$ и $D_1B$ делятся точкой пересечения $O$ пополам. Аналогично доказывается, что диагонали

Параллелепипед (от греч. parallelogram 1 ‘параллельный’ и греч. ἐπι-πεδον ‘плоский’) — это призма, основанная на параллелограмме, или (эквивалентно) многогранник с шестью гранями, каждая из которых является параллелограммом.

Параллелепипед, свойства прямоугольного параллелепипеда

Геометрия, образованная двумя равными параллелограммами на параллельных уровнях и их вершинами, соединенными с двумя парами прямоугольников на параллельных уровнях между параллельными уровнями, называется параллелепипедом (Рисунок 1).

Параллелограммы, составляющие параллельное расщепление, называются параллельными сторонами, стороны прямоугольников — параллельными сторонами, а вершины в одинаковых точках — параллельными вершинами.

1$ и $D_1B$ и $A_1C$ и

Геометрия — это раздел математики, который занимается изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и связанных с ними положений. Для облегчения преподавания геометрия подразделяется на планетарную и стереометрическую. … …. Энциклопедия Кольера.

Параллелепипед, свойства прямоугольного параллелепипеда

Геометрия, образованная двумя равными параллелограммами на параллельных уровнях и их вершинами, соединенными с двумя парами прямоугольников на параллельных уровнях между параллельными уровнями, называется параллелепипедом (Рисунок 1).

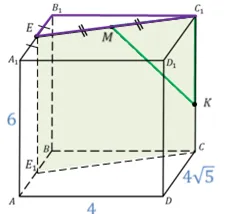
Параллелограммы, составляющие параллельное расщепление, называются параллельными сторонами, стороны прямоугольников — параллельными сторонами, а вершины в одинаковых точках — параллельными вершинами.

1$ делятся точками их пересечения пополам. Но, так как $O$ центр диагоналей $A_1C$ и $D_1B$, то все диагонали пересекаются в этой точке.

Теорема доказана.

[/H1toH2]

Одна из вершин основания (F) равноудалена от всех вершин нижнего основания параллелепипеда. Вместе с нижней диагональю (AC) они образуют равнобедренный треугольник ∆AFC. AF = AC по договору. AF — край фигуры.

Формулы параллелепипеда

Чтобы найти ответ на этот вопрос, недостаточно знать только свойства геометрии. Для нахождения площади и объема геометрической фигуры также может потребоваться несколько типов.

Основание базы находится тем же способом, что и соответствующая экспонента прямоугольника или прямоугольника. Можно выбрать прямоугольные основания по отдельности. Как правило, при решении задачи легче работать с перспективами, основанными на прямоугольниках.

В задачах тестирования также необходимо найти тип параллельной внешней поверхности.

Примеры решения типовых заданий ЕГЭ

Задание 1.

Даны: прямоугольники с размерами 3, 4 и 12 см. Найдите длины главных диагоналей фигуры. РЕШЕНИЕ: Решение геометрической задачи должно начинаться с построения правильного и четкого графика, на котором можно найти значения, рассматриваемые как «заданные». Следующая схема является примером правильной конструкции для рассматриваемых условий.

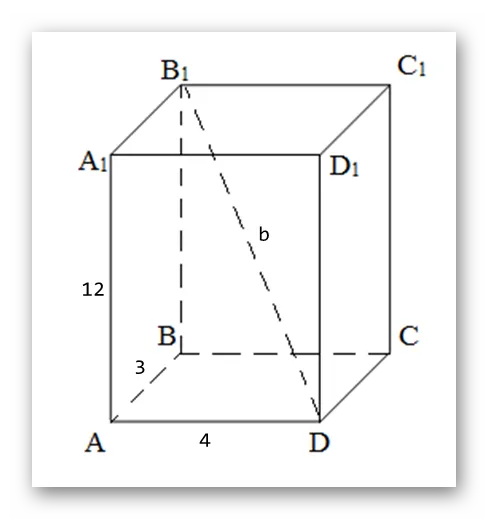
Имея план, который напоминает и напоминает нам обо всех свойствах геометрического тела, мы окажемся на единственно правильном пути решения задачи. Применяя четвертое состояние параллели, получаем следующее уравнение

После несложных вычислений получаем уравнение b2 = 169. Следовательно, b = 13. Ответ на задачу найден, и на его поиск и оформление не должно уйти более 5 минут.

Задание 2.

Обозначение: наклонная параллельная кожа с боковыми краями 10 см, прямоугольная KLNM с размерами 5 и 7 см. это часть формы, параллельная указанному прыщу. Найдите площадь стороны четырехугольной призмы. РЕШЕНИЕ: Сначала необходимо составить конкретный план.

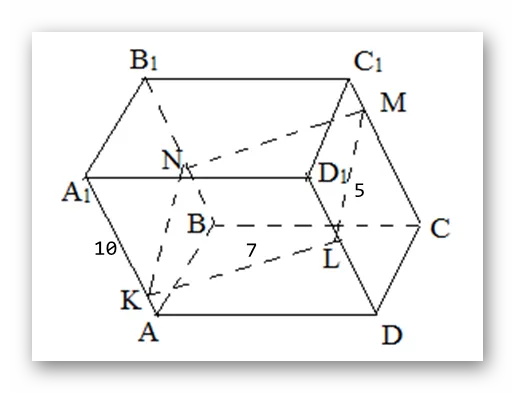
Чтобы решить эту проблему, необходимо использовать разум. Из диаграммы видно, что стороны KL и AD неравносторонние, как и пары ML и DC. Однако границы этих прямоугольников явно равны.

Поэтому внешняя площадь равна площади, умноженной на пупырышки AA1 пересекающего участка, так как пупырышки перпендикулярны пересекающему участку. Ответ: 240 см2.

Чтобы решить эту проблему, необходимо использовать разум. Из диаграммы видно, что стороны KL и AD неравносторонние, как и пары ML и DC. Однако границы этих прямоугольников явно равны.

Параллелепипед

Параллелепипед (от греч. parallelogram 1 ‘параллельный’ и греч. ἐπι-πεδον ‘плоский’) — это призма, основанная на параллелограмме, или (эквивалентно) многогранник с шестью гранями, каждая из которых является параллелограммом.

Содержание

Существует несколько видов параллельных видов:.

• — это параллелепипед, у которого все грани — Основные элементы

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется Свойства

• Параллелепипед симметричен относительно середины его диагонали.
• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
• Противолежащие грани параллелепипеда параллельны и равны.
• Квадраты длины диагонали прямоугольной параллели равны сумме квадратов ее трех измерений.

Основные формулы

Прямой параллелепипед

Латеральный s_warr.=р _� *H, где p _� — Периметр основания, H — высота

Общая поверхность s_п= s_warr.+2s _� где s _� — Базовая площадь

Прямоугольный параллелепипед

Латеральный s_warr.= 2c(a+b), где a и b — стороны основания, а c — прямоугольник

Общая поверхность s_п= 2(ab+bc+ac)

Объем V = ABC, где a, b и c — размеры прямоугольных параллелей

Поверхность: «ширина =» «высота =» » /> объем: «ширина =» «высота =» » />, является пимпочкой куба.

Произвольный параллелепипед

Объем и пропорции наклонных параллельных релевантностей часто определяются как 2:215.