Видите, наш прямоугольник разделен на два треугольника. Эта линия, соединяющая вершины противоположных углов прямоугольника, называется диагональю. Затем два других угла соединяются линией.
Квадрат
Квадрат — это обычный четырехугольник. У него все стороны и углы равны друг другу. Квадрат — это особая форма прямоугольника и особая форма ромба. Площадь квадрата равна квадрату его сторон. Тогда существует второе уравнение: площадь квадрата равна половине площади его диагонали.
Квадрат — это четырехугольник со сторонами и углами, равными друг другу.

Диагональ квадрата — это часть, соединяющая две противоположные вершины.
Прямоугольники, ромбы и прямоугольники также являются квадратами, если они имеют прямые углы, стороны одинаковой длины и диагонали.
\{\(⌘ угол ABC+\ угол BCD+\ угол CDA+\ угол DAB=360 ^ \)

{\ угол BAC=\ угол BCA=\ угол CAD=\ угол ACD=45 ^ \)

Квадрат является ромбом \(\ стрелка вправо \)\(45 ^ \). Тогда Ў(Ў угол А \), и Ў(Ў угол С \) от \(45 ^ \).
Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам
{\ угол AOB=\ угол BOC=\ угол COD=\ угол AOD=90 ^ \)

Поскольку квадрат является прямоугольником, \(\\ Rightarrow \) диагонали равны — поскольку он является ромбом, \(\ Rightarrow \) диагонали перпендикулярны. Кроме того, поскольку это прямоугольник, \(⌘ правая стрелка ⌘) диагональ делится пополам в точке пересечения.
Точки A, B, C и D называются вершинами четырехугольника, а отрезки AB, BC, CD и AD — его сторонами. Вершины A и C, B и D называются его противоположными вершинами. AB и CD, BC и AD называются его противоположными сторонами.
Прямоугольник (понятие, определение):
Прямоугольник — это четырехугольник, у которого все углы правильные (каждый угол равен 90 градусам).
Прямоугольник — это четырехугольник, у которого все углы правильные.
Прямоугольник — это четырехугольник, две противоположные стороны которого равны друг другу, четыре угла равны друг другу и каждый угол равен 90 градусам.

Аналогично, четырехугольник (греческий квадрат) — это геометрическая фигура (многоугольник), состоящая из четырех точек (вершин) (третья не на одной прямой) и четырех отрезков (сторон), соединяющих эти точки линиями.
Длинная сторона прямоугольника называется длиной прямоугольника, а короткая сторона — шириной прямоугольника.
Свойства прямоугольника:
1. прямоугольник является прямоугольником — его противоположные стороны попарно параллельны.

2.Противоположные стороны прямоугольника равны.
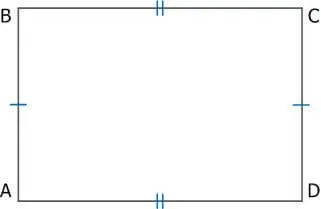
3. стороны прямоугольника являются его высотой.
4. смежные стороны прямоугольника всегда перпендикулярны.

5. каждый угол прямоугольника правильный и равен 90 градусам. Сумма всех углов прямоугольника равна 360 градусам.

6. диагонали прямоугольника равны.
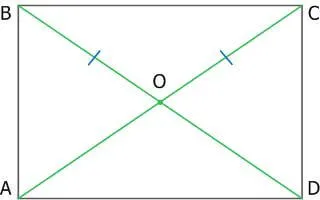
7. каждая диагональ прямоугольника делит его на два одинаковых правильных треугольника.
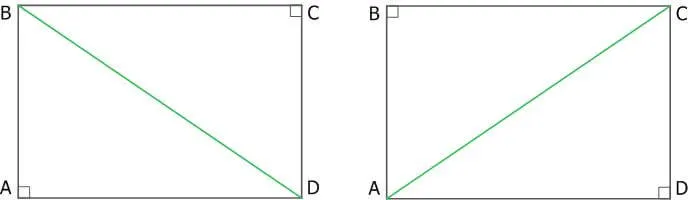
8.Квадрат диагонали прямоугольника равен сумме квадратов двух соседних сторон (это следует из теоремы Пифагора).
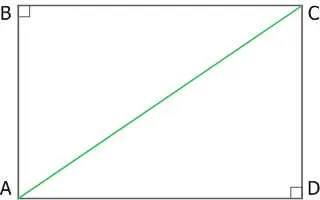
9.Диагональ прямоугольника делится пополам своим пересечением.
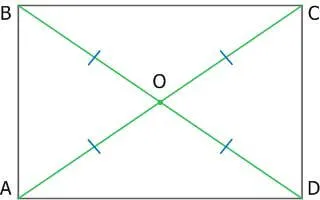
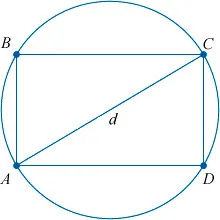
10.Вокруг любого прямоугольника можно нарисовать окружность. Диагональ прямоугольника равна диаметру окружности.
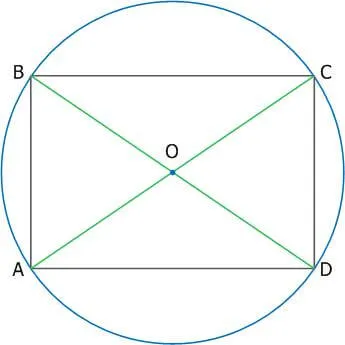
AC и BD — диаметры окружности и диагонали прямоугольника.
11.Точка пересечения диагоналей называется центром прямоугольника и является центром контура.
12.Прямоугольник может содержать только один выгравированный круг и один, если все его стороны равны, т.е. квадрат.
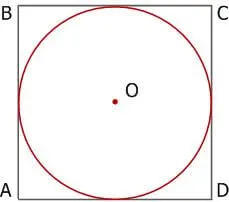
Формулы прямоугольника:
Длина прямоугольника, b ширина прямоугольника, d диагональ и диаметр вокруг прямоугольника, r радиус вокруг прямоугольника, граница прямоугольника, s прямоугольник.
Виды сторон прямоугольника (длина и ширина прямоугольника): a
Тип диагностики прямоугольника:.
Тип периметра прямоугольника:.
Тип площади прямоугольника:.
Тип радиуса окружности, описанной вокруг прямоугольника:.
Примечание: ©Фото https://www.pexels.com и https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
- Концепция инновационного развития общественного производства – осуществления Второй индустриализации России на период 2017-2022 гг. (106 949)
- Экономика Второй индустриализации России (103 205)
- Этилен (этен), получение, свойства, химические реакции (29 530)
- Программа искусственного интеллекта ЭЛИС (29 474)
- Метан, получение, свойства, химические реакции (26 578)
- Крахмал, свойства, получение и применение (26 050)
- Природный газ, свойства, химический состав, добыча и применение (25 168)
- Целлюлоза, свойства, получение и применение (24 320)
- Пропилен (пропен), получение, свойства, химические реакции (23 565)
- Прямоугольный треугольник, свойства, признаки и формулы (23 276)
Поиск технологий
О чём данный сайт?
Сайт посвящен научным разработкам автора в области экономики и научным идеям по осуществлению второй индустриализации России.
— Экономика второй индустриализации России, — Теория, методология и инструменты инновационного развития — Реализация второй индустриализации России — Организационные механизмы второй индустриализации России — Справочник по пионерным технологиям.
Мы не продаем продукты, технологии и т.д. Производители и изобретатели! Вам необходимо связаться с нами напрямую!
Мы ведем переговоры с производителями и изобретателями инновационных технологий в стране и даем рекомендации по их использованию.
О Второй индустриализации
Применение второй российской индустриализации основано на качественно новых научных данных (теория, методология и инструменты), разработанных авторами.
Конечным результатом второй индустриализации России является рост благосостояния всех членов общества. Это средний человек, бизнес и государство.
Вторая индустриализация России — это совокупность научных, технологических и других инновационных идей, планов и разработок, широко применимых к практике хозяйственной деятельности в краткосрочной перспективе (3-5 лет) и обеспечивающих новое прогрессивное развитие общества высокого качества. в ближайшие 50-75 лет.
Россия — первая страна, сделавшая это сложное открытие, — станет лидером мирового сообщества, чего не сможет сделать ни одна другая страна в течение столетий.
10.Вокруг любого прямоугольника можно нарисовать окружность. Диагональ прямоугольника равна диаметру окружности.
Трапеция
Стол — это четырехугольник, две стороны которого параллельны, а две другие — нет.
Основание — это параллельная сторона, две другие стороны — боковые.
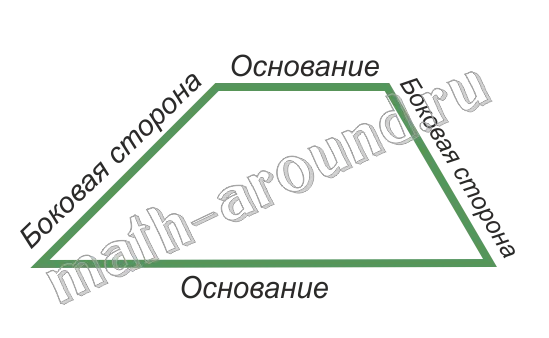
| Трапеция называется равнобедренной , если ее боковые стороны равны. |  |
| Трапеция, один из углов которой прямой, называется прямоугольной . |  |
Средняя линия трапеции соединяет боковые стороны.
Средняя линия трапеции параллельна основанию и равна половине ее суммы.
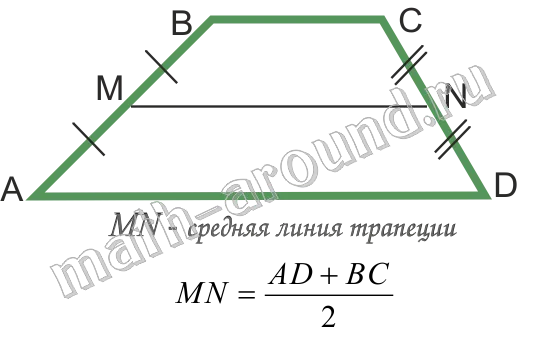
Площадь трапеции:.
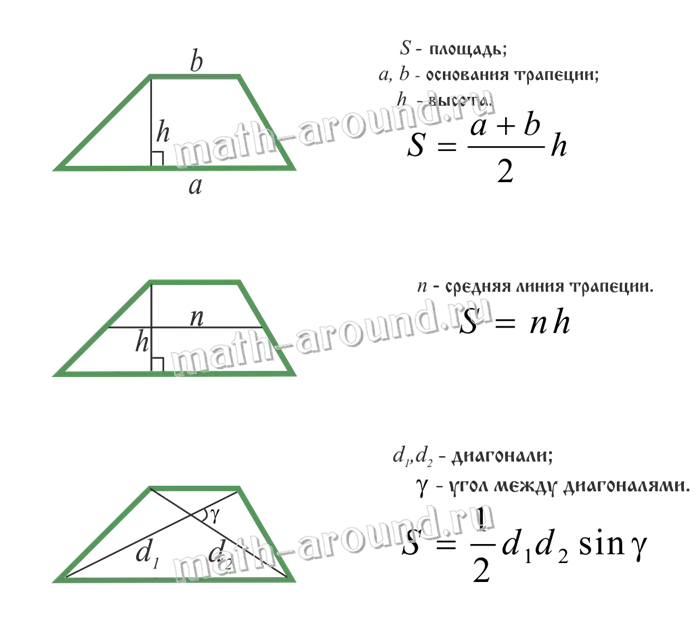
Ромб — это прямоугольник, у которого все стороны равны.
Область ромба:.
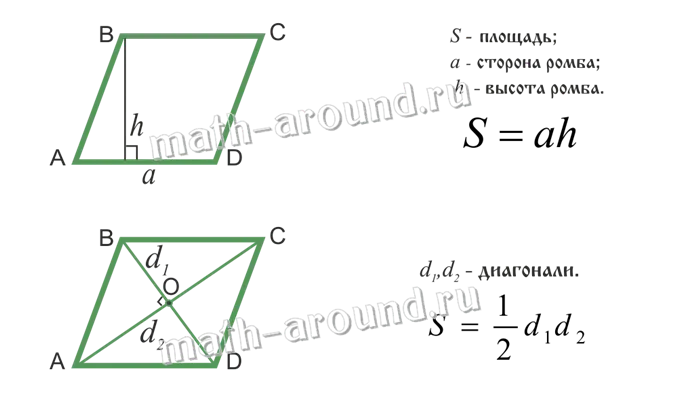
Прямоугольник
Прямоугольником называется прямоугольник, у которого все углы равны.
Синус прямоугольника:.
Если диагонали прямоугольника равны, то этот прямоугольник является прямоугольником.
Площадь прямоугольника:.

Квадрат
Квадрат — это прямоугольник, у которого все стороны равны.
Свойства:.
Квадрат обладает всеми свойствами прямоугольника и ромба (так как прямоугольник — это прямоугольник, а квадрат — это прямоугольник со всеми сторонами, то есть ромб).
Площадь квадрата:.

- отправить денежный перевод с карты на карту мгновенно и без комиссий по ссылке. Ссылка на перевод. В поле «Добавьте комментарий» необходимо указать «в дар» или «подарок» .
- оставить комментарий ниже.
Комментарии к этой позиции:.
(Мне очень понравилась эта статья) Все интересно и понятно) Очень полезно! (Спасибо)
В прямоугольнике противоположные стороны равны и параллельны друг другу. Большая сторона называется длиной (обозначается A), а меньшая — шириной (обозначается B). В прямоугольнике на рисунке длины равны AB и CD, а ширины — A C и B. D. Они также перпендикулярны основанию (т.е. высоте).
Диагонали прямоугольника
Как уже говорилось выше, диагонали прямоугольников (соединяющие противоположные углы) равны между собой.
Это можно доказать с помощью известной теоремы Пифагора. В нем говорится, что «сумма квадратов перпендикуляров правильного треугольника равна квадрату гипотенузы».

В данном случае гипотенуза — это диагональ прямоугольника, который делится на два равных правильных треугольника. Из этого следует теорема Пифагора.

Свойства прямоугольника
Свойства прямоугольника включают следующие утверждения
-
Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
- длины – более длинная пара сторон. Обычно обозначаются латинской буквой, например, a ;
- ширины – более короткая пара сторон. Чаще всего обозначаются как b .
-
У прямоугольника равны противоположные стороны.



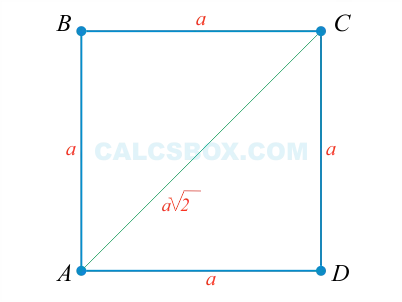
![]()



Она равна 6 см. Затем измеряется нижняя часть, т.е. сторона, противоположная верхней части. Поэтому она называется другой стороной и также равна 6 см.
Что такое прямоугольник: определение, свойства, признаки, формулы
В этом материале описывается определение, свойства и характеристики одной из основных геометрических фигур — прямоугольника. В ней также представлены формулы, которые можно использовать для нахождения его площади и периметра.
Прямоугольник — это четырехугольник, у которого все углы равны 90° (т.е. они прямые).

Прямоугольник состоит из
Прямоугольник обычно записывается путем перечисления его вершин. В нашем случае — ABCD.
Примечание: Прямоугольник — это разновидность прямоугольника.
Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника находятся в параллельных и равных парах.

Свойство 2
Длина и ширина прямоугольника перпендикулярны друг другу, а значит, одновременно и высоте.

Свойство 3
Соединение средних точек сторон прямоугольника образует ромб.
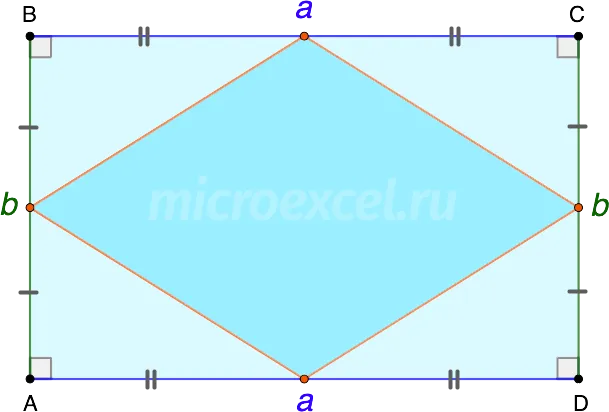
Свойство 4
Квадраты на диагонали (d) прямоугольника равны сумме квадратов на соседних сторонах.
d 2 = a 2 + b 2
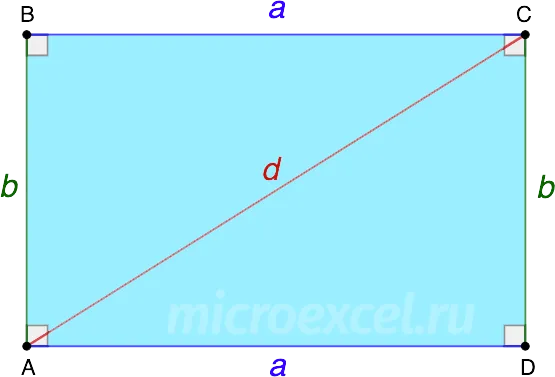
Это основано на теореме Пифагора, которую можно применить к любому ортогональному треугольнику, образованному путем деления диагоналей прямоугольника.
Свойство 5
Диагонали прямоугольника равны и делятся пополам в точке пересечения.
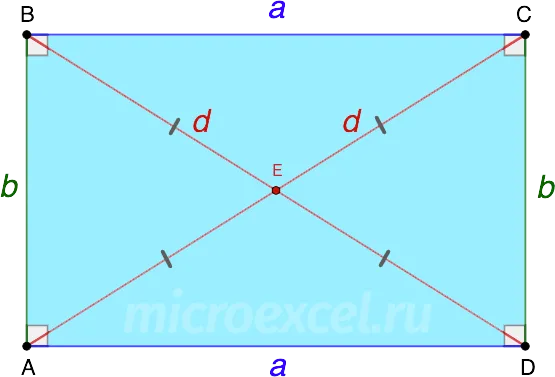
Свойство 6
Любой прямоугольник может быть заключен в рамку радиусом (R), равным половине диагонали прямоугольника.
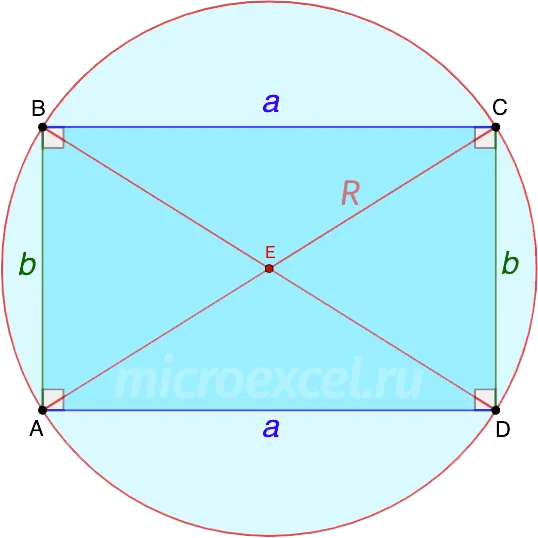
Поэтому диаметр круга равен общей длине диагонали прямоугольника.
Квадраты являются частным случаем ромбов, прямоугольников или прямоугольных треугольников. В отличие от этих фигур, все углы правильные, а четыре стороны равны. Квадрат — это обычный четырехугольник.
Прямоугольник. Свойство его сторон. Квадрат
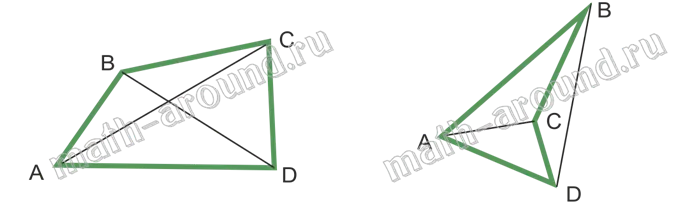
В этом уроке Королева Математики объясняет, как найти прямоугольник между разными фигурами и что такое квадрат. Царица также показывает детям свойства прямоугольников.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам из комплекта, необходимо приобрести его в каталоге и добавить в личный шкафчик.


Конспект урока «Прямоугольник. Свойство его сторон. Квадрат»
-Здравствуйте, мои дорогие дети! Сегодня мои друзья и помощники плюс и минус заняты очень важным делом. Присоединяйтесь к нашему турниру по поиску неисправностей. И нам необходимо знакомиться с новыми темами. Поэтому я решил объяснить вам это сам. Но прежде чем мы начнем, я прошу вас отгадать загадку.
У двери, за столом, в книге.
О какой фигуре мы сегодня говорим? Вы уже поняли, что речь идет о прямоугольниках.
Теперь внимательно посмотрите на экран. Что вы видите на экране?
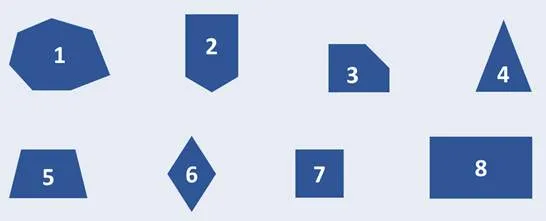
Конечно, эти фигуры можно назвать одним словом — многоугольники. Существуют фигуры с тремя углами, четырьмя углами, пятью углами и т.д.
Вы уже знакомы с темой углов. И помните, что углы бывают разные — прямые, тупые, острые.
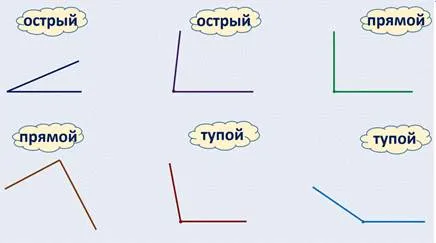
А фигура, о которой мы сегодня поговорим, называется прямоугольником. Вы слышите это? Прямой угол. Если мы скажем, что это прямоугольник, то вы догадаетесь, что это означает, что у него прямой угол.
Посмотрите на наш план. Затем с помощью линейки посмотрите, какая фигура находится под прямым углом. Посмотрите на первую диаграмму.
Это шестиугольник. Давайте проверим его углы.
Как видите, эта фигура имеет прямой угол, а остальные фигуры — непрямые.
Посмотрите на вторую диаграмму: это пятиугольник.
У него два прямых угла, остальные три — непрямые.
Третий также является пятиугольником. У него три прямых угла. Четвертый — треугольник. Пятый — это стол.
Эти фигуры не имеют правильных углов.
Но седьмой и восьмой:.
Все эти фигуры имеют правильные углы.
Такие фигуры с прямыми углами называются прямоугольниками. Обратите внимание, что обе фигуры с правильными углами являются четырехугольниками, т.е. имеют четыре угла и четыре стороны. Конечно, существуют различные четырехугольники. Однако прямоугольник называется четырехугольником только в том случае, если все углы правильные.
А теперь я предлагаю вам познакомиться с интересными свойствами прямоугольника. Вам понадобятся линейка и компас.
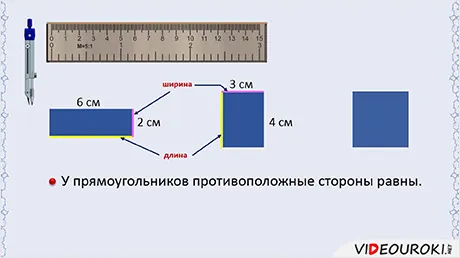
Перед нами прямоугольник. Посчитайте верхнюю часть.
Она равна 6 см. Затем измеряется нижняя часть, т.е. сторона, противоположная верхней части. Поэтому она называется другой стороной и также равна 6 см.
Они составляют 2 см. Рассчитайте другую сторону. Они также составляют 2 см. Следовательно, равны ли противоположные стороны прямоугольника? Или это только прямоугольник. Проверьте другой прямоугольник.
Стороны равны и противоположные стороны равны.
Теперь мы можем с абсолютной уверенностью сказать, что у прямоугольника равные стороны. Поэтому, называя длины сторон прямоугольника, не обязательно называть каждую сторону. Одна длинная сторона и только одна сторона может быть подписана. Ведь вы знаете, что противоположные стороны прямоугольника равны. Поэтому, подписав одну из сторон, вы знаете, что другая сторона этого прямоугольника также будет такой же длины.








