Эти прямые не параллельны, потому что коэффициенты X имеют разные значения. Чтобы найти углы, образованные разрезом, переведите каждое уравнение в векторную форму.
Угол между пересекающимися прямыми: определение, примеры нахождения
В данном материале рассматривается понятие угла между двумя пересекающимися прямыми. В первом разделе объясняется, что это такое, и приводятся фотографии. Далее объясняется, как находить знаки, косметику и углы (рассматривая отдельно уровень уровней и трехмерное пространство).
Чтобы понять, что такое угол при пересечении двух прямых, нужно вспомнить сами определения угла, перпендикуляра и пересечения.
Две прямые называются пересекающимися, если они имеют общую точку. Эта точка называется точкой пересечения двух линий.
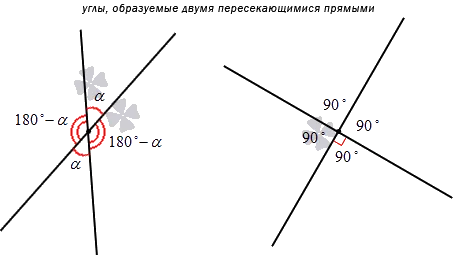
Каждая линия делится на лучи, исходящие из точки пересечения. Две прямые образуют четыре угла, оба из которых примыкают к вертикали. Если вы знаете меру одного из них, вы можете определить остальные.
Предположим, вы знаете, что один из углов равен a. В этом случае угол, перпендикулярный к нему, также равен a. Чтобы найти оставшиеся углы, нужно вычислить разность 180°. Если a равно 90°, то все углы прямые. Прямые линии, пересекающиеся под прямым углом, называются перпендикулярными (понятию перпендикулярности посвящена другая статья).
Давайте перейдем к формулировке основного определения.
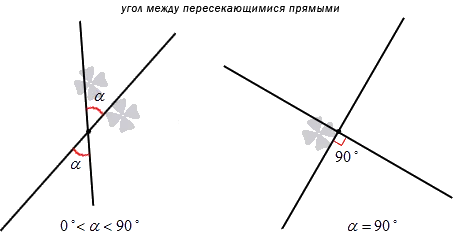
Угол между двумя прямыми линиями — это меньшая масштабная мера из четырех углов.
Из этого определения можно сделать важные выводы. Величина угла в этом случае может быть выражена любым действительным числом в пространстве (0, 90. Если линии перпендикулярны, то угол между ними в каждом случае равен 90 градусам.
Как найти угол между пересекающимися прямыми на плоскости
Нахождение угла между двумя пересечениями полезно для решения многих практических задач. Существуют различные варианты решения проблемы.
Вначале можно использовать геометрический метод. Если вы знаете что-то о дополнительных углах, вы можете использовать свойства равных или подобных фигур и соотнести их с нужным вам углом. Например, если вам известны стороны треугольника и нужно вычислить угол между прямой линией с этими сторонами, теорема косинусов создает вагину. Если в нашей ситуации речь идет о прямоугольных треугольниках, то знание синуса, косинуса и тангенса угла также будет полезно.
Метод координат также очень полезен при решении такого рода задач. Давайте объясним, как правильно их использовать.
Имеется прямоугольная (декартова) система координат O X Y с двумя прямыми. Пусть они и b символизируют их. Линии могут быть описаны определенными уравнениями. Начальная линия имеет точку пересечения m. Как определить необходимый угол между двумя линиями (объясним это в терминах a)?
Начните с формулировки основного принципа нахождения угла при определенных условиях.
Мы знаем, что понятие прямой линии, такой как направляющий вектор или обычный вектор, тесно связано с понятием прямой линии. Учитывая уравнение прямой линии, можно получить координаты этих векторов. Это можно сделать с помощью двух линий, которые пересекаются в одно и то же время.
Угол, образованный двумя пересекающимися прямыми, можно найти, используя
- угла между направляющими векторами;
- угла между нормальными векторами;
- угла между нормальным вектором одной прямой и направляющим вектором другой.
Далее рассмотрим каждый метод в отдельности.
1. предположим, что существует прямая A с вектором A→ = (a x, y) и прямая B с вектором B→ (b x, b y). Затем мы отводим два вектора A→ и b→ от пересечения. Затем мы видим, что каждый из них находится на своей линии. Затем есть четыре варианта их взаимного расположения. См. фото:.
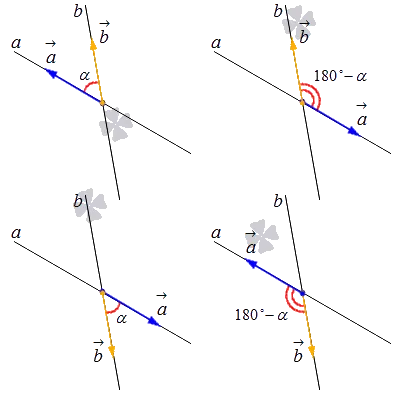
Если угол между двумя векторами тупой, то это и есть искомый угол между линиями A и B. Если он тупой, то искомый угол — это угол, примыкающий к углу a → b ^ ^. Таким образом, если α = α→, то β→ ^α→α→β≤≤ 90°, а если α = 180°-α→, то β→ ^, α→β→ ^, β→ ^> 90°.
Предполагая равенство углов, полученное уравнение можно переписать следующим образом: β→ ^ = — cosα→, для β→ ^, a→β→ ^> 90°.
В последнем случае был использован уменьшенный тип. Итак.
cosαCosα→, β→ ^, cosα→, β→≥0 — cosα→, β→ ^, cosα→, β→ ^, cosα→, β→ ^, cos→ ^, β→ ^< 0 ⇔ cos α = cos a →, b → ^
Запишите последний тип словами:.
Косинус угла, образованного двумя пересекающимися прямыми, равен угловой мере угла между векторами.
Общая форма вида косинуса угла между двумя векторами A→ = (a x, a y) и b→ = (b x, b y) имеет вид
cos a→, b→ ^ = a→, b→ ^ a→-b→= a x -b x + a y- b y a x 2 + a y 2 -b x 2 + b y 2
Из этого типа можно извлечь косинус угла между двумя определенными линиями.
Как вычислить угол между пересекающимися прямыми в пространстве
Расчет таких углов может быть ограничен вычислением координат направляющих векторов и определением величины углов, образующих эти векторы. Поэтому для примера мы используем те же рассуждения, что и раньше.
Предположим, у нас есть прямоугольная система координат в трехмерном пространстве. Определите два ряда A и B в точке сечения m. Чтобы вычислить координаты векторного водителя, нам нужно знать уравнения этих линий. Пусть A→= (a x, a y, a z) и b→= (b x, b y, b z). Чтобы вычислить косинус угла, используйте тип
cos a = cos a →, b → ^ = a →, b → a → — b → = a x -b x + a y -b y + a z -b z a x 2 + a y 2 + a z 2 -b x 2 + b y 2 + B Z 2
Чтобы найти сам угол, вам нужен этот тип.
a = a r c cos a x -b x + a y -b y + a z -b z a x 2 + a y 2 + a z 2 -b x 2 + b y 2 + b z 2
Существует прямая линия, определенная в трех измерениях уравнением x 1 = y -3 = z + 3-2. Известно, что она пересекает ось O Z. Вычислите угол пересечения и косинус этого угла.
Углы рассчитаны в следующей таблице. Запишите координаты -A→= (1, -3, -2) направляющего вектора в первой строке. Для приложенной оси в качестве направляющего вектора можно взять координатный вектор k→= (0, 0, 1). Необходимые данные получены и могут быть добавлены к нужному типу.
cos a = cos a→, k→ ^ = a→, k→a→ — k→= 1-0-3-0-2-1 1 2 + ( — 3)2 + (- 2)2 -2- 0 2 + 0 2 + 0 2 + 0 2 + 1 2 = 2 8 = 1 2
Результат показывает, что требуемый угол равен R C COS 1 2 = 45°.
Пример 3: Решение: найти вектор прямой: объяснить уравнение прямой, используя точки и векторы прямой. Поскольку одна из координат направляющего вектора равна нулю, уравнение переписывается как.
Простейшие задачи с прямой на плоскости. Взаимное расположение прямых. Угол между прямыми
Мы продолжаем рассматривать эти бесконечные линии. На уроке Уравнения мы узнали об основных типах уравнений, векторных движителях линий и их обычных векторах. Данная статья является логическим продолжением темы и посвящена следующим формальным вопросам для опытного путешественника. Таблицы кликов будут предоставлены в ближайшее время.
о-о-о-о-о-о-о-о-о… Какая это банка!Вы. (Предложение самому себе =) Но расслабление поможет позже, тем более что сегодня я приобрел соответствующие аксессуары. Теперь перейдем к первому разделу. Я надеюсь, что к концу статьи буду чувствовать себя лучше.
Взаимное расположение двух прямых
Рассмотрим две прямые линии, заданные уравнением в общем виде.
Если зрители поют от радости. Две линии:.
3) или пересекаются в одной точке:.
Помощь для тупых: запомните математическую символику перекрестка, это случается очень часто. Символизм означает, что прямая пересекает прямую в точке.
Как определить взаимное расположение двух прямых?
Две линии согласуются только в том случае, если их коэффициенты пропорциональны, т.е. если имеет место равенство, поскольку существует такое число «лямбда».
Учитывая линии, образуются три уравнения, каждое со своим коэффициентом. Таким образом, каждое уравнение показывает, что эти линии совпадают.
На самом деле, если все коэффициенты уравнений умножить на -1 (смена знака) и все коэффициенты уравнений умножить на 2, мы получим одно и то же уравнение.
Второй случай — когда прямые параллельны.
Две прямые параллельны тогда и только тогда, когда коэффициенты при переменных гладкие.
В качестве примера рассмотрим две строки. Проверьте пропорциональность соответствующих коэффициентов этой переменной.
Однако ясно, что линия параллельна.
Третий случай — когда линии пересекаются.
Две линии пересекаются только в том случае, если коэффициенты внутри переменных несоизмеримы. Другими словами, не существует такого значения ‘лямбда’, для которого справедливо равенство!
Теперь сформируем систему линий.
Из первого уравнения, а затем из второго: это означает, что системы несовместимы (нет решения). Поэтому переменные факторы не пропорциональны.
Вывод: линии пересекаются.
Для реальной задачи можно использовать только что рассмотренную схему решения. Кстати, это в первую очередь напоминает алгоритмы управления векторами, участвующими в курсе, концепцию линейной (не)зависимости от векторов. Векторная база. Но есть и более цивилизованные пакеты:.
Нахождение взаимного расположения рядов:.
Решение основано на исследовании векторов направления рядов.
(a) Найдите директоров рядов из уравнений.
Вычислите определение координат этих векторов. Это означает, что векторы не склеиваются, а линии пересекаются.
Для всего я поставил камень с маркером на перекрестке:.
1) Если не понятно, начните с векторов из статьи для чайников. 2) Если не ясно, как найти вектор направления линии, обратитесь к линейному уравнению уровня. 3) Если непонятно, какое отношение имеет тождество к векторам, перейдите сюда — смысл линейной (не)зависимости векторов. Базовый вектор.
(Остальные перепрыгнут через камень и двинутся вперед, будучи непосредственно увековеченными в Куссеуме =)
b) Найдите вектор направления линии.
Прямые имеют одинаковый вектор направления и поэтому параллельны или совпадают. Нет необходимости даже вычислять идентификаторы.
Очевидно, что коэффициенты при переменных видны.
Проверьте, правильно ли составлено уравнение.
(c) Найдите вектор в направлении линии.
Перпендикулярные прямые. Расстояние от точки до прямой. Угол между прямыми
Начнем с типичной и очень важной проблемы. В первой части вы узнали, как построить линию, параллельную заданной линии. Теперь зев у ног курицы повернут на 90 градусов.
Как построить прямую, перпендикулярную данной?
Эта линия задается уравнением декартовой системы координат. Составьте уравнение вертикальной прямой, проходящей через точку.
Решение: узнайте это по отгадке. Лучше найти вектор линии. Если линия перпендикулярна, то фокус прост.
Постройте нормальный вектор из уравнения:, это будет вектор линии.
Составьте уравнение прямой из точек и направляющих векторов.
Давайте разработаем геометрический эскиз:.
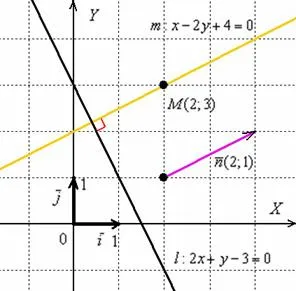
Да … Оранжевое небо, оранжевое море, оранжевый верблюд.
Детальная проверка решений: да.
1) Нарисуйте вектор направления из уравнения и используйте произведение градиентов векторов, чтобы сделать вывод, что линия перпендикулярна.
Кстати, можно использовать и обычные векторы, что еще проще.
2) Проверьте, удовлетворяют ли точки полученному уравнению.
Опять же, это легко сделать устно.
Для уравнений и точек декартовой системы координат найдите точку пересечения вертикальных линий.
Это пример независимого решения. Поскольку в проблеме много этапов, полезно создать решение по пунктам.
Наше увлекательное путешествие продолжается:.
Расстояние от точки до прямой
Перед нами прямой участок реки, и наша цель — добраться до реки кратчайшим путем. Здесь нет препятствий, и лучший маршрут — по вертикальной линии. Другими словами, расстояние точки от прямой — это длина вертикального отрезка.
Геометрические расстояния традиционно обозначаются греческой буквой «ро». Пример:- Расстояние от точки «um» до линии «e».
Расстояние точки от прямой в декартовых координатах задается следующим образом
Найдите расстояние точки от прямой линии
Решение: все, что нам нужно сделать, это добавить числа в формулу и выполнить расчет.
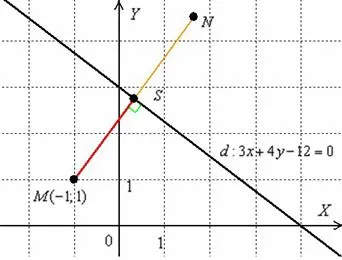
Нарисуем ее: расстояние точки от прямой в точности равно длине красной части прямой. Если вы рисуете на клеточной бумаге в масштабе 1 единица = 1 см (2 кв. дюйма), вы можете измерить расстояние обычной линейкой.
Рассмотрим другое произведение того же типа.
Как построить точку, симметричную относительно прямой?
Задача состоит в том, чтобы найти координаты точки, симметричной относительно прямой. Советуем вам сделать это самостоятельно, но вот алгоритм решения с промежуточными результатами.
1) Найдите прямую, перпендикулярную прямой.
Найдите пересечение линий:.
В этом уроке обе функции будут подробно описаны.
Это среднее геометрическое системы двух линейных уравнений с двумя неизвестными. Это две (в основном) прямые линии, которые пересекаются в плоскости.
Формула угла между прямыми
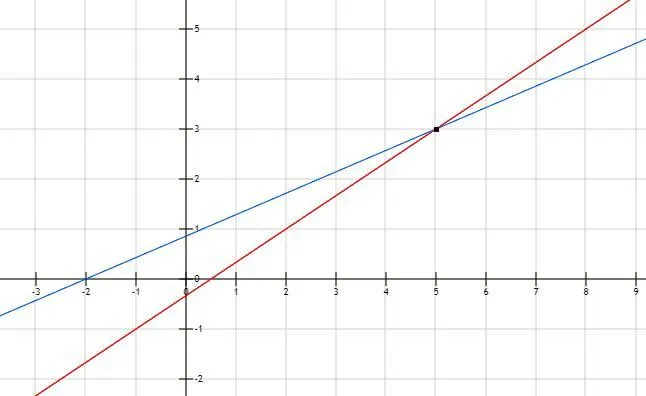
На плоскости две прямые пересекаются или параллельны друг другу. В пространстве эти вариации дополняются возможностью пересечения линий. Независимо от конфигурации, применяемой к этим одномерным геометрическим объектам, угол между ними всегда может быть определен следующим уравнением
где v1¯ и v2¯ — векторы первой и второй строк соответственно. Поскольку числитель является элементом калиброванного изделия, тупые углы исключаются и рассматриваются только острые углы.
Векторы v1¯ и v2¯ могут быть заданы в двух или трех координатах, а формула для угла φ остается неизменной.
Параллельность и перпендикулярность прямых
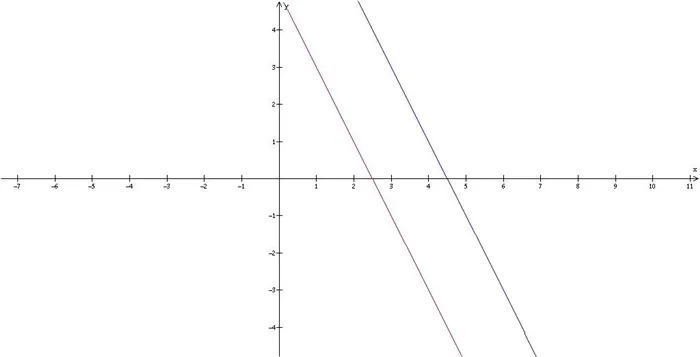
Две прямые считаются параллельными, если угол между ними, вычисленный с помощью приведенных выше типов, равен 0°. Чтобы определить, параллельны ли прямые, не обязательно вычислять угол f. Если одна направляющая является подобным вектором другой прямой, то есть : Q
где Q — действительное число.
Если уравнение линии задано в виде:.
Параллельно только в том случае, если коэффициенты при x равны.
Мы можем доказать это, рассмотрев, как коэффициент K выражается через координаты вектора прямой наводки.
Если угол пересечения линий равен 90°, они называются перпендикулярными. Пока вычисляется только ступенчатое произведение v1¯ и v2¯, перпендикуляры линий не обязательно должны определяться углом φ сброс.
Тип угла φ может также использоваться для уровней, которые пересекаются между собой. Результаты должны быть интерпретированы соответствующим образом. Вычисленное значение f указывает на величину угла между векторами направлений прямых, которые не пересекаются и не параллельны.
Задача №1. Перпендикулярные прямые
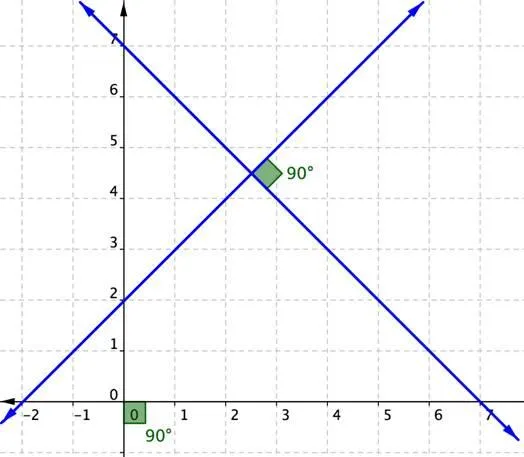
Известно, что уравнение прямой линии имеет вид.
Необходимо определить, являются ли эти линии перпендикулярными или нет.
Чтобы ответить на поставленный выше вопрос, достаточно вычислить степенное произведение направляющих векторов, соответствующих координатам (1; 2) и (-4; 2). У нас есть: .
0, что означает, что эти линии пересекаются под прямым углом, т.е. перпендикулярно.
Это разделение и точный выбор задач зависят от конкретной ситуации с конкретным студентом и преподавателем (время, продолжительность, педагогические, методические, психологические…) .
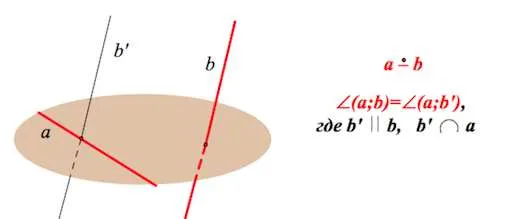
Угол между скрещивающимися прямыми
Угол между двумя прямыми — это угол между двумя прямыми, соответствующими этим пересекающимся прямым.
(Одна прямая не может двигаться вдоль себя, но ограничена параллельностью одной из прямых с другой прямой).