Производная функции. Что такое производные функции

В зависимости от цели, применения и используемого математического аппарата применяются различные методы производных. Например, N-производные могут быть записаны в следующей символике

Производная функции

Производные (функции точек) являются фундаментальным понятием в дифференциальном исчислении и описывают скорость изменения функции (конкретной точки). Он определяется как предел отношения приращения функции к приращению аргумента, при котором приращение аргумента стремится к нулю. （ Функция с конечной производной (в данный момент времени) называется дифференцируемой (в этот момент времени).

Процесс вычисления производных называется дифференцированием. Обратный процесс нахождения первой производной называется интегрированием.

Определение

Предположим, что в некоторой окрестности точки производная функции является числом, которое можно выразить следующим образом

если

Определение производной функции через предел

Даже в некоторых точках производные функции, если они есть, называются пределами.

Общепринятые обозначения производной функции

Обратите внимание, что последнее обычно обозначает производную по времени (теоретическая инженерия).

Дифференцируемость

Производная в точке
Для дифференцируемой в в окрестности

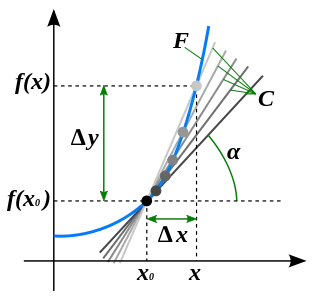
Тангенс угла наклона касательной прямой

Геометрическое значение производных. На графике функции выберите положение фермы x₀ и соответствующая линия f (x₀). Вблизи точки x₀ Выбирается произвольная точка x. Вторичный (первая открытая серая линия c₅). Расстояние Δx = x — x₀ Нулевая и вторичная превращаются в касательные (постепенно темнеющая линия c₅ — c₁). Угол наклона этой касательной является производной от x₀ .

Если функция то в окрестности

Функция в момент времени — это угол или тангенс наклона касательной линии.

Скорость изменения функции.

Пусть выражает мгновенную скорость движения в момент времени выражает мгновенное ускорение в момент времени

В общем случае производная функции представляет собой скорость изменения функции в точках

На своих уроках я использую термин «производная» вместо термина «производный». Например, сумма слагаемых равна сумме корней. Есть ли в этом смысл? Ну, это хорошо.

Основные свойства производных.

Если в некоторой точке x существуют конечные производные функций v = v(x) и u = u(x), то существуют также производные суммы, разности, произведения и коэффициента этих функций.

1.
2.
3.

4.,.

5 …

1. производные сложных функций.

Если функция y = f (x) имеет производные в точке x₀ Функция y = g(x) имеет производную в точке y₀ = f (x₀), то сложная функция h(x) = g(f(x)) также имеет производную при x₀ Учитывая следующие факты

2. условия, подходящие для монотонности функции.

Если все точки пространства (a; b) подчиняются неравенству:.

Тогда функция y = f (x) возрастает на этом интервале.

Если y = f (x) сводится к (a; b).

3. экстремальные необходимые условия функции.

Если точка x₀ оказывается точкой экстремума функции y = f(x) и в этой точке есть производная

4. знак максимума функции.

Если функция y = f (x) определена в пространстве (a; b), то она непрерывна в пространстве и x₀ точка максимального значения функции.

5. знак минимального значения функции.

Если функция непрерывна в пространстве и пространстве, то точка x₀ является точкой минимума функции.

Правило отыскания наибольшего и наименьшего значений функции.

Чтобы вычислить наибольшее и наименьшее значения функции с конечным числом критических точек в пространстве, необходимо определить значение для склонения к нулю или вычислить точку точек) определенной области, которая не существует. Функция в каждой критической точке и на границе пространства выбирает максимум и минимум из полученных значений.

Пусть в некоторой окрестности точки . Производной функции является такое число A, что функцию в окрестности

Тангенс угла наклона касательной линии.

Если у функции , тогда в окрестности

Функция f в определенный момент времени называется угловым голосом или наклоном касательной линии.

Скорость изменения функции..

Пусть выражает мгновенную скорость движения в момент времени выражает мгновенное ускорение в момент времени

В общем производная функции выражает скорость изменения функции в точке, т.е. скорость протекания процесса, который описан зависимостью

Производная функции y = f (x) в точке x.₀является пределом отношения приращения функции к приращению аргумента в этой точке, но приращение аргумента стремится к нулю, когда оно конечное, таков предел.

Решение производной для чайников: определение, как найти, примеры решений

Без знания производных и способов их вычисления совершенно невозможно решать задачи по физике или математические примеры. Производные являются одним из наиболее важных понятий в математическом анализе. Именно этому фундаментальному смыслу мы решили посвятить настоящую статью. Что такое производные, каково их физическое и геометрическое значение и как вычисляются производные функции? Все эти вопросы можно свести к одному. Как мы понимаем деривативы?

Ежедневные сообщения на канале Telegram содержат полезную информацию для студентов всех дисциплин.

Геометрический и физический смысл производной

Предположим, что существует функция f (x), заданная на некотором интервале (a, b). Точки x и x0 принадлежат этому интервалу. Если x меняется, то меняется и сама функция. Изменение аргумента — это разница между значениями x и x0. Эта разница описывается как дельта x и называется приращением аргумента. Изменение или возрастание функции — это разница между значениями функции в двух точках. Определение производного:.

Производная функции в точке — это предел отношения приращения функции в данной точке к приращению аргумента, при котором аргумент стремится к нулю.

Иначе это можно записать следующим образом.

В чем смысл поиска такого предела? Это:.

Геометрический смысл производных: производная функции в точке равна тангенсу угла между осью OX и тангенсом графика функции в этой точке.

Физическая концепция производных: производная пути по времени равна скорости линейного движения.

Действительно, из школьных уроков все знают, что скорость — это коэффициент пути x = f(t) и времени t. Это средняя скорость за определенный период времени.

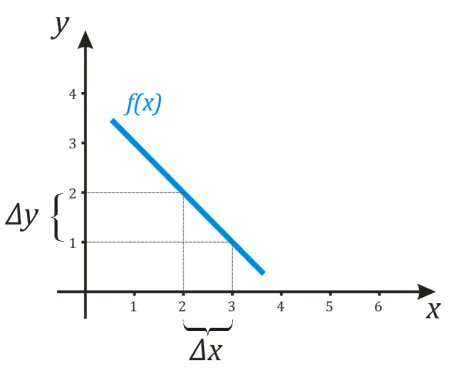
Чтобы узнать скорость движения в момент времени t0, нужно вычислить предельную скорость.

Кстати, читайте в другой нашей статье, что такое ограничения и как их решить.

Ниже приведен пример реального применения деривативов. Предположим, что тело движется по закону.

Нам нужно найти скорость в момент времени t=2c. Вычислим производные:.

Правила нахождения производных

Процесс нахождения производных называется дифференцированием. Функция, производные которой лежат в одной точке, называется дифференцируемой функцией.

Как вы находите производные? По определению, вам нужно создать соотношение между функцией и аргументом increase и вычислить предел, когда аргумент increase стремится к нулю. Конечно, можно было бы вычислить таким образом все производные, но на практике это очень долгий путь. Все уже предварительно вычислено. Ниже приведена таблица основных производных и правила вычисления производных, включая производные сложных функций, с подробными примерами.

Кстати, сейчас действует 10% скидка на все работы читателя.

Правило первое: выносим константу

Константы могут быть удалены из символов производных. Более того, это должно быть сделано. При решении математических примеров возьмите за правило: если выражение можно упростить, его нужно упростить.

Пример. Вычислим производную:.

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разностной функции.

Мы не будем доказывать эту теорему, но рассмотрим практический пример.

Найдите производные функции.

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле

Пример: найти производную функции:.

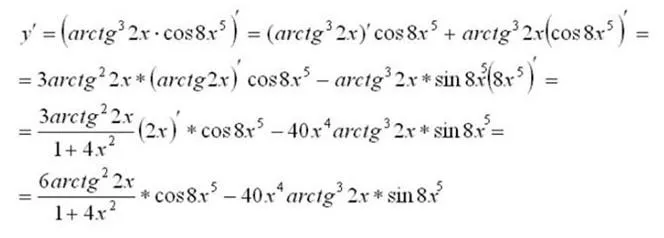
Здесь важно сказать кое-что о вычислении производной сложной функции. Производная сложной функции равна произведению производной этой функции на промежуточный член производной промежуточного члена независимой переменной.

В приведенном выше примере мы сталкиваемся с выражением.

В данном случае промежуточный аргумент равен восьми умноженным на пятую степень. Чтобы вычислить производную такого выражения, мы сначала считаем производную внешней функции по промежуточному аргументу, а затем умножаем ее на производную промежуточного члена независимой переменной.

Правило четвертое: производная частного двух функций

Человек, определяющий производные коэффициентов двух функций: человек, определяющий производные коэффициентов двух функций.

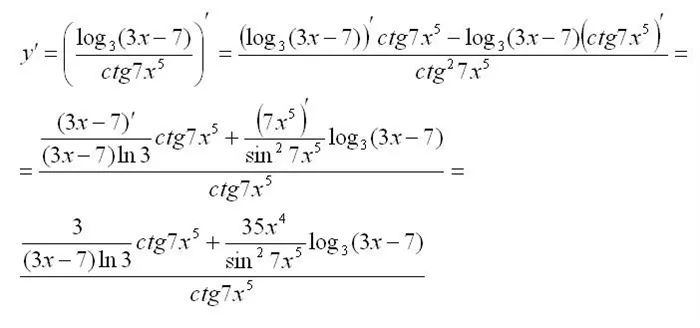
Мы попытались с нуля поговорить о глупых деривативах — проблеме, которую не так-то просто решить. Обратите внимание, что эта проблема не так проста, как кажется. Будьте осторожны при подсчете производных, так как примеры часто имеют TRAP.

Если у вас есть вопросы по этой или любой другой проблеме, вы можете обратиться в отдел по работе со студентами. Даже если вы никогда раньше не вычисляли производные, вы сможете решать самые сложные тесты и задачи за короткое время.

Иван Колобков, также известный как Джони. Заочник маркетолога, аналитика и копирайтера. Очень перспективный молодой писатель. Он любит физику, необычные вещи и творчество К. Буковски.

Такая зависимость — скорость изменения функции по умолчанию — также может быть описана функцией. Таким образом, если функция достаточно изменчива, чтобы позволить ей быть непрерывной, можно использовать как первую, так и вторую производные. Давайте проанализируем это подробнее.

Понятие производной на интервале

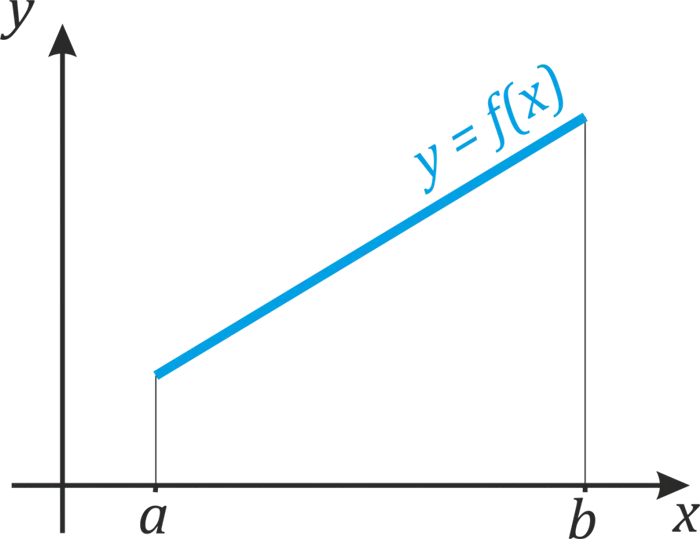
Предположим, есть несколькоЛинейный функции определённый вво Вселенной. \; b \). Что вы подразумеваете под словом «определить»? Это означает, что в течение этого интервала для каждого \(x \) мы можем найти соответствующее \(y \) (см., например, следующий график).

Придадим этому интервалу \(a; b \) некоторое значениеаргумент (a; b \) — \(x_a \). Это соответствует точке ⌘ (a \) на графике и значению функции (y_a \).

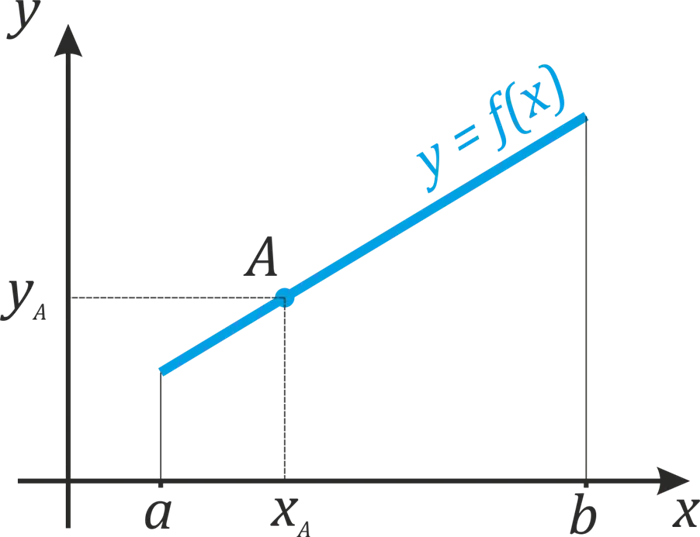
Далее, дадим некоторое приращение ߡ (Δx\) к выбранному значению ߡ (x_a \). Этот символ\(dx \) читается как «дельта x», что означает величину изменения x. Поэтому мы увеличиваем значение ɛ(x_a \) до ɛ(Δx\). Затем она движется вдоль вала ⌘(x \) и встречает ⌘(x_b \), который равен ⌘(x_a+Δx⌘). Очевидно, что «расстояние» между Ў(x_b \) и Ў(x_a \) равно именно Ў(Δx\) (см. график), т.е. увеличению аргумента. И этот аргумент аргумента является «длиной» рассматриваемого нами пространства.

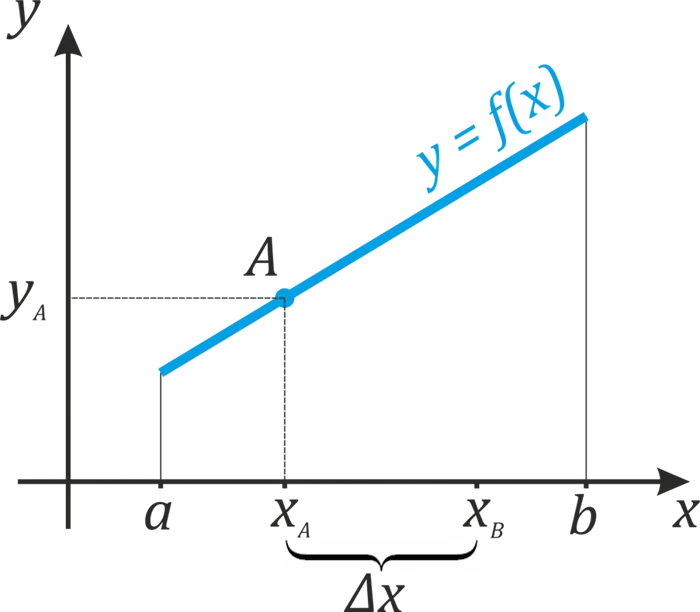
Значение аргумента ⌘ (x_b \) соответствует значению точки ⌘ (b \) и функции (y_b \) на графике. \Расстояние между \(y_b \) и ዄ(y_a \) символизируется как Some \(dy \) (как мы делали с осью ዄ(x \)). Что такое \(dy \)? Подумайте об этом — был аргумент, равный ߡ(x_a \), соответствующий значению функции ߡ(y_a \). Затем мы увеличили аргумент на \(Δx\) (в \(x_b \)) и функция также увеличилась до \(y_b \). \Чему равна ˉ(dy \) разность между ˉ(y_b \) и ˉ(y_a \)? Правильно, это приращение значения функции от функции.

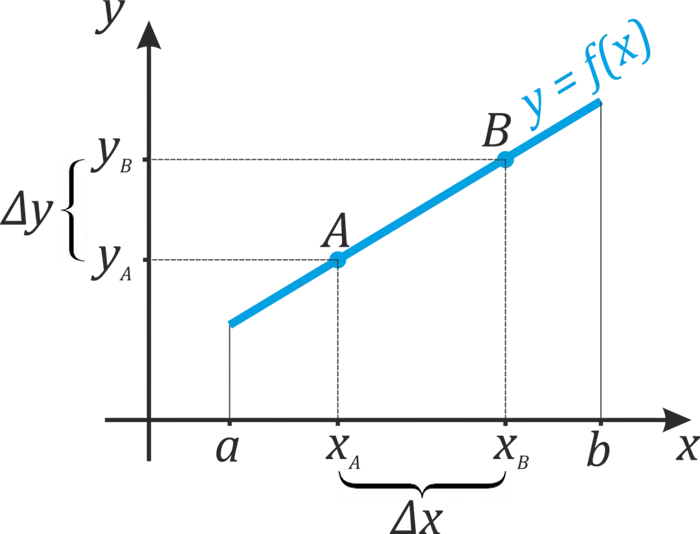
Поэтому деление \(dy \) на \(Δx\) дает производную функции от \(x_a \) к \(x_b \) к \(Δx\). В этом и заключается суть термина «производная» по пространству. Это число, получаемое делением длины DY на длину соответствующего сегмента\(Δx\).

Производная на интервале — это отношение приращения функции на интервале к ширине этого интервала (то есть приращению аргумента).

Внимание! Это определение не является математически строгим и является «неявным» по причинам понимания.

Другими словами, производная интервала показывает, насколько изменилась функция в зависимости от изменения аргумента функции. Иначе: производная в пространстве показывает скорость возрастания функции в этом пространстве.

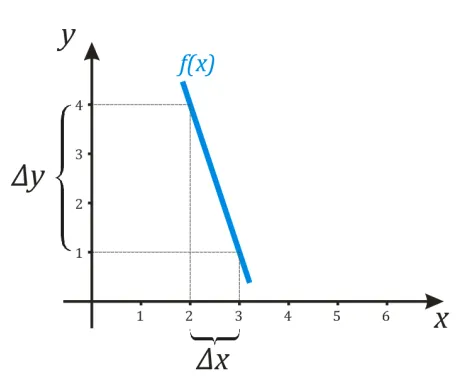
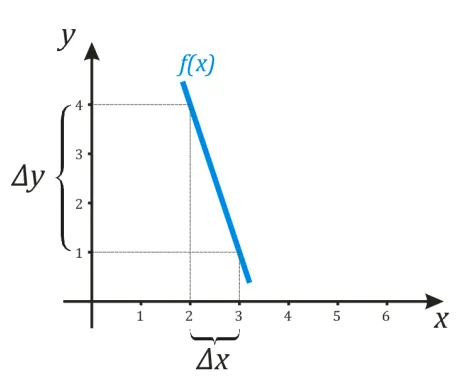
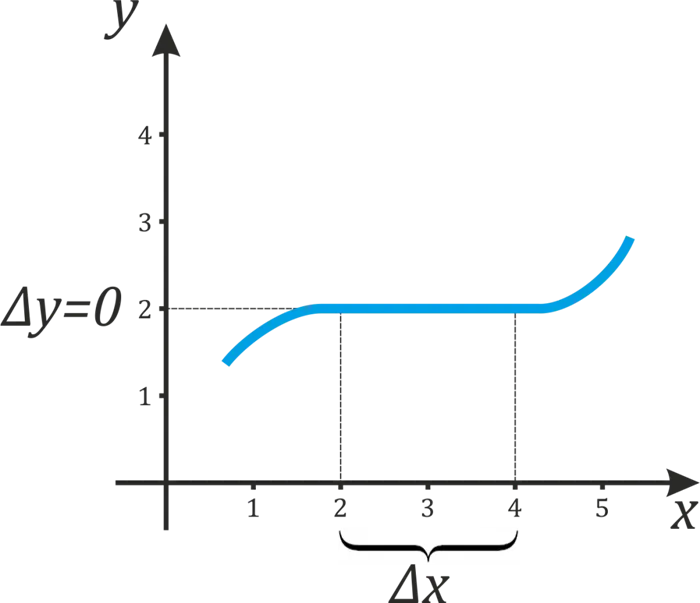
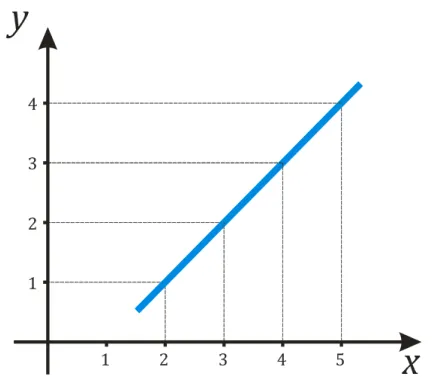
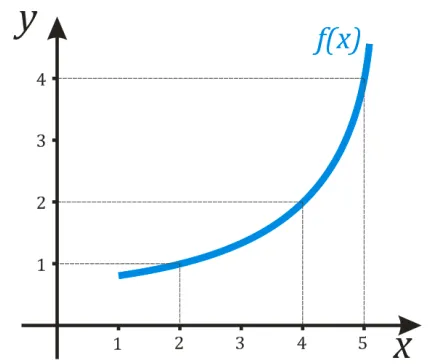
Действительно, посмотрите на два графика ниже.

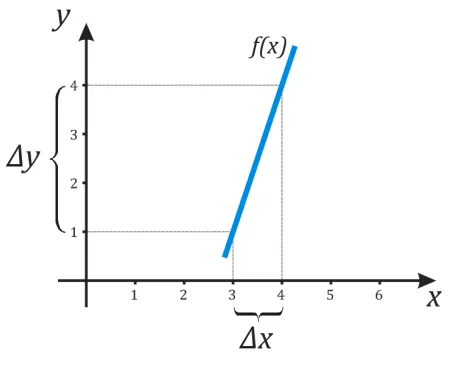
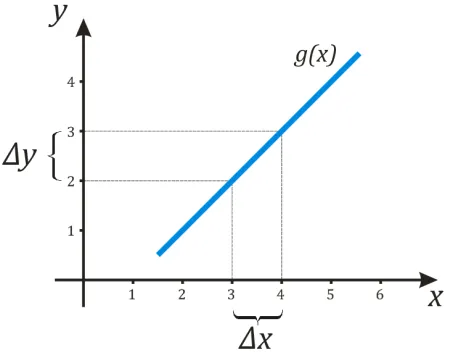
На первом графике, по мере увеличения аргумента от \(3 \) до \(4 \), функция увеличивалась от \(1 \) до \(4 \). Поэтому \(∆x = x_B-x_A = 4-3 = 1 \) и \(∆y = y_B-y_A = 4-1 = 3 \), т.е. значение производной в пространстве \((3; 4)\) равно \(ɛ frac = \ frac = 3 \).

Рассмотрим функцию. Какова разница в данный момент времени? Это вспомогательная функция, часто используемая в расчетах, и зависит от двух переменных: и. Как найти значение разности в определенный момент времени? -Для этого мы произвольно увеличиваем значение. Производная функции в точке находится по следующему уравнению.

Примеры на приращение функции и аргумента

Пример 1

= 2, находим приращение функции.

Решение: очевидно, что начальное значение аргумента равно 2, а конечное значение равно 2,5. Найдите значение функции в этих двух точках и .

Итак

Пример 2

Заданная функция. Найдите приращение с .