Призма (математика). Что является основанием призмы

Призма — это многогранник, в котором две грани находятся в равных многоугольниках и параллельных плоскостях, а все остальные грани — прямоугольные.

Призма в геометрии — определение, формулы и примеры

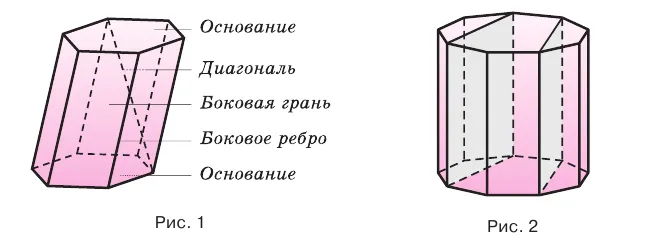
Равные многоугольные грани призмы лежат в параллельных плоскостях и называются основанием призмы, а остальные грани призмы называются гранями. Края сторон, которые не принадлежат основанию, называются боковыми гранями. Линия, соединяющая две вершины, не принадлежащие одной плоскости, называется диагональю призмы (рис. 1). Плоскость, проходящая через два ребра призмы, которые не принадлежат одной плоскости, называется диагональной плоскостью, а сечение призмы диагональной плоскостью называется диагональным сечением. На рисунке 2 показаны два диагональных сечения призмы.

Призмы можно разделить на треугольники, квадраты, пятиугольники и т.д., в зависимости от количества сторон основания. Призма, показанная на рис. 1, шестиугольная, а на рис. 2 — непентагональная.

Различают прямые и наклонные призмы в зависимости от того, перпендикулярны ли боковые грани призм к их основаниям. Обычно прямые призмы рисуют с перпендикулярными боковыми гранями.

Если основанием призмы является правильный многоугольник, то такая призма называется нормальной призмой. Все стороны прямой призмы прямоугольные, а все стороны нормальной призмы — равные прямоугольники.

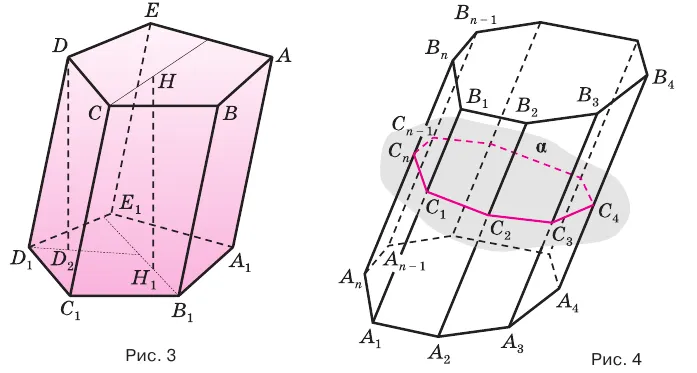
Перпендикуляр, проведенный из какой-либо точки одного основания призмы к плоскости другого основания, называется высотой призмы. На рисунке 3 показаны две высоты призмы

Боковые стороны образуют грани призмы, а грани вместе с основанием образуют полную поверхность призмы.

Стороны призмы равны произведению периметра ее вертикального сечения и длины боковых граней.

ЭВИДЕНЦИЯ.

Пусть имеется . Пересечем ее плоскостью , стороны которого перпендикулярны сторонам параллелограммов, составляющим боковую поверхность призмы. Поэтому для боковой поверхности

（В (1) мы считаем, что все боковые грани призмы равны друг другу, а в (2) мы считаем, что сумма множителей вертикального сечения и боковых граней призмы равна.

Результат 1.

Площадь боковых граней линейной призмы равна произведению периметра ее основания и высоты.

Фактически, перпендикулярная часть призмы равна ее основанию, а боковые грани — ее высоте.

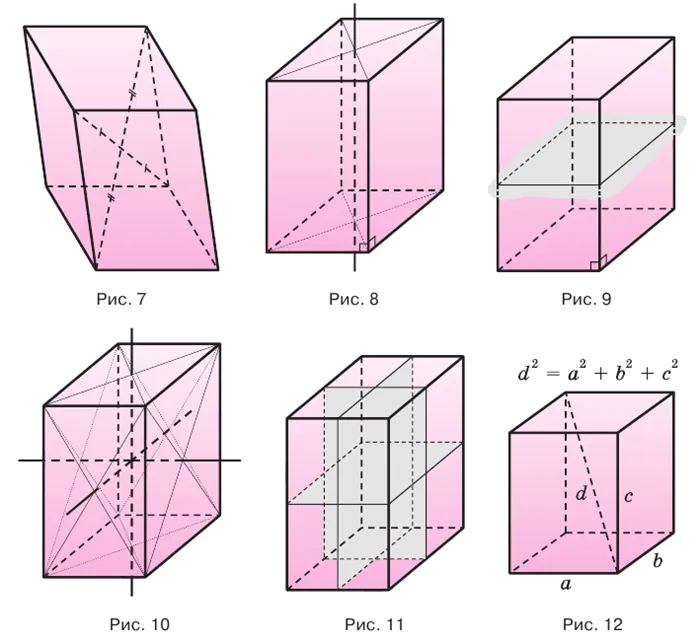
Особым видом призмы является параллелепипед, т.е. призма с прямоугольным основанием. Как и призмы, параллелограммы могут быть прямыми или косыми. Прямой параллелограмм с прямоугольным основанием называется прямоугольником. Прямоугольник с тремя ребрами, исходящими из одной вершины и равными друг другу, называется кубом.

Каждая сторона параллелограмма — это параллелограмм, из которых прямоугольный параллелограмм имеет прямоугольные стороны, а прямоугольный параллелограмм — все стороны.

Призма и её сечения

Вы уже знакомы с призмами. Тем не менее, позвольте мне напомнить вам определение призмы и ее свойства.

Призма — это многогранник, две стороны которого имеют равные n углов (основание) и лежат в параллельных плоскостях, а остальные n сторон — прямоугольные (рис. 22).

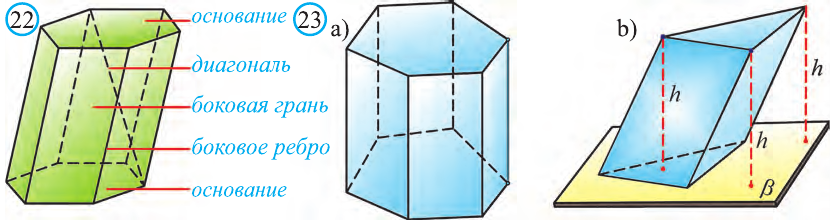
В зависимости от того, перпендикулярны ли грани призмы к основанию, призмы различают как прямые или косые. На рис. 23.a показана линейная призма, а на рис. 23.b — наклонная призма. Очевидно, что стороны линейной призмы прямоугольные.

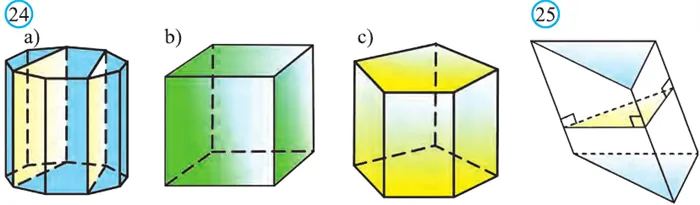
Если дно прямой призмы представляет собой правильный многоугольник, то она называется нормальной призмой (рис. 24). Стороны нормальной призмы — равные прямоугольники.

Перпендикулярная прямая, опускающаяся из одной точки одного основания в другую, называется его перпендикуляром (рис. 23.b).

Части призмы, проходящие через соответствующие диагонали основания, называются диагональными сечениями (рис. 24.a), и их число равно числу диагоналей в одном из оснований.

Вертикальное сечение призмы — это сечение, перпендикулярное всем ее поперечным граням (рис. 25). Поскольку число диагоналей равно числу диагоналей выпуклого n-квадрата, число диагоналей n-квадратной призмы также равно числу диагоналей n-квадратной призмы.

В каждом диагональном сечении призмы можно провести две диагонали. Следовательно, n -угольная призма имеет

Для наклонной треугольной призмы расстояния между гранями сторон равны 7 см, 15 см и 20 см соответственно. Найдите расстояние между наибольшим поперечным ребром и противоположным поперечным ребром.

Известно, что расстояние между параллельными прямыми равно длине перпендикуляра, проведенного из любой точки одной прямой в другую. Далее определяются длины кромок вертикальной секции ABC (рис. 26). Наибольшее ребро призмы проходит через наибольшую сторону этого отрезка AC = 20 см. Расстояние от вершины призмы B₂Â Â Â₁ в плоскости стороны BD треугольника ABC.

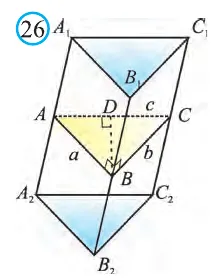
Тогда, используя формулу Герона, имеем

С другой стороны,

Следовательно, см.

Ответ: 4,2 см.

Параллелепипед и куб

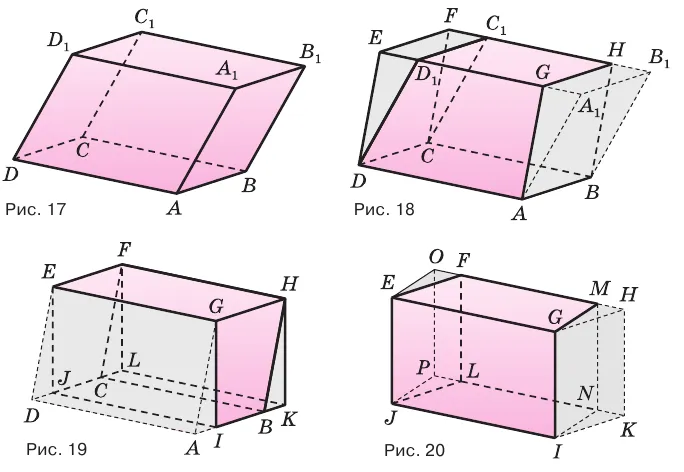
Призма с прямоугольным основанием называется параллелограммом (рис. 27). Параллелограммы, как и призмы, могут быть прямыми (рис. 27.a) и наклонными (рис. 27.b).

Поверхности параллелограмма, не имеющие общей вершины, называются противоположными поверхностями.

• —12 рёбер, каждые четыре из которых равны (рис. 28.а),
• —6 граней, которые попарно параллельны и равны (рис. 28.b),
• —4 диагонали, которые пересекаются и точкой пересечения делятся пополам (рис. 28.с),
• —точка пересечения диагоналей — центр его симметрии (рис. 28.с). Прямой параллелепипед имеет ось симметрии (рис. 28.d) и плоскость симметрии (рис. 28.e).

Объем призмы

Одним из свойств, характеризующих геометрические объекты в пространстве, является понятие объема. Каждый объект (тело) занимает определенную часть пространства. Например, по сравнению со спичечным коробком, кирпич занимает больше места. Для сравнения этих частей вводится понятие объема.

Объем — это величина, числовое значение которой обладает следующими свойствами

1. Любое тело имеет определённый объём, выраженный положительным числом.
2. Равные тела имеют равные объёмы.
3. Если тело разбито на несколько частей, то его объём равен сумме объёмов этих частей.
4. Объём куба, ребро которого равно единице, равен единице.

Объем — как и длина и площадь, это количество. В зависимости от выбора единицы длины, кубический объем измеряется в кубических единицах.

1 см 3, 1 дм 3, 1 м3 и т.д.

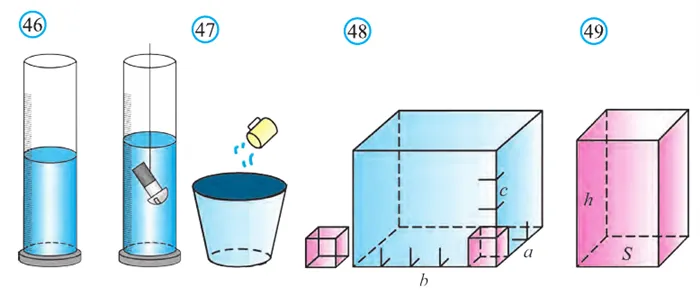
Объем тела может быть измерен или рассчитан различными способами. Например, объем небольшого предмета можно измерить в мензурке с мелкими делениями (шкалой) (рис. 46). Объем ведра также можно измерить, заполнив водой емкость одного объема (рис. 47). Однако измерить объем всех объектов таким образом невозможно. В таких случаях объемы могут быть рассчитаны различными способами. Далее они рассматриваются без доказательств.

Объём параллелепипеда

Теорема. Объём прямоугольного параллелепипеда равен произведению трех его измерeний (рис.48):
Следствие. Объём прямоугольного параллелепипеда равен произведению площади его основания на высоту (рис. 49):
Теорема. Объём произвольного параллелепипеда равен произведению площади его основания на высоту (рис. 50):

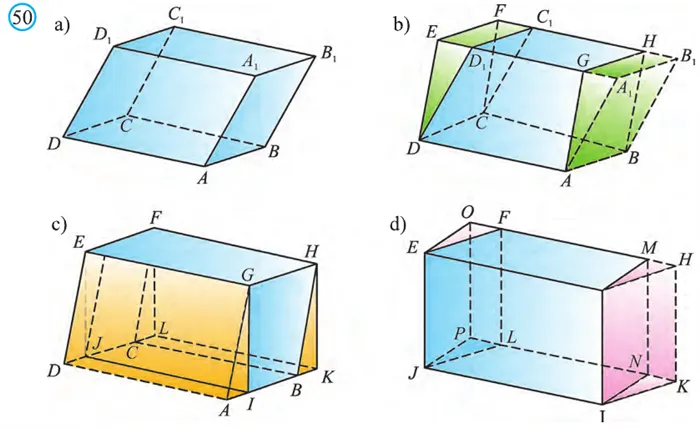
Эта характеристика основана на выводах, сделанных выше. На рисунке 50 показано, как некоторые параллелограммы преобразуются в прямоугольники. Свойство доказано с использованием только

Нахождение объёма призмы

Теорема. Объём прямой призмы равен произведению площади его основания на высоту (рис. 51):

Доказательство. 1 ящик. Предположим, что основанием призмы является правильный треугольник (рис. 51.a). Эта призма может быть расширена прямоугольной равносторонней призмой (рис. 51.b).

Если объем данной призмы, площадь ее основания и высота равны V, S и h, то объем полученного параллелепипеда, площадь его основания и высота равны 2V, 2S и h соответственно.

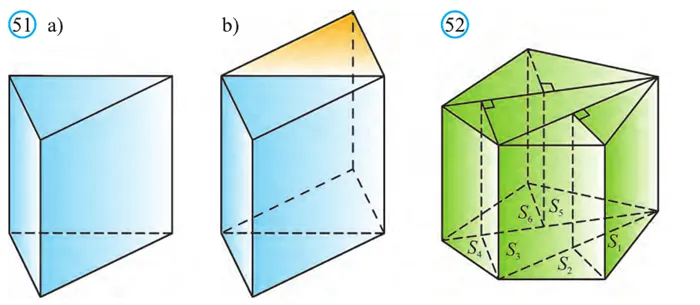
Поэтому.

2 случай. Пусть S — площадь произвольной n — угольной прямой призмы и h — её высота. Основание призмы — n -угольник делится диагоналями на треугольники, каждый из которых можно разделить на прямоугольные треугольники (рис. 52). В результате данная призма разделится на конечное число прямых призм, основания которых являются прямоугольными треугольниками. Высоты этих призм равны h , а сумма площадей оснований этих призм равна площади основания данной призмы:

Объем призмы равен сумме объемов треугольных призм, из которых она состоит.

Призма — это многогранник, две грани которого являются конгруэнтными многоугольниками в параллельных плоскостях, а остальные грани — прямоугольники с общими с этими многоугольниками сторонами.

Свойства призмы

• 1. Основания призмы являются равными многоугольниками.
• 2. Боковые грани призмы являются параллелограммами.
• 3. Боковые ребра призмы параллельны и равны.
• 4. Объём призмы равен произведению её высоты на площадь основания:

• 5. Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Призмы могут быть прямыми и наклонными.

Прямая призма — это призма, все стороны которой перпендикулярны основанию.

Стороны прямой призмы равны произведению высот вокруг основания.

Наклонная призма — это призма, у которой по крайней мере одна боковая грань не перпендикулярна основанию.

Сторона наклонной призмы равна произведению вертикальных сечений на длину бокового торца. Объем наклонной призмы равен произведению площадей вертикальных сечений боковых граней.

Нормальные призмы — это прямые призмы с правильным многоугольным основанием.

Свойства правильной призмы

• 1. Основания правильной призмы являются правильными многоугольниками.
• 2. Боковые грани правильной призмы являются равными прямоугольниками.
• 3. Боковые ребра правильной призмы равны.

Полуортогональные многогранники или архимедовы/двойные многогранники или тела Каталана (Кубо Тренер/Лободеда, 22 Близнеца/Пятидесятник/Додеканиса, Ролл/Делос Фикар, Ломбоид Куба/Дидиакадрос

Фонд Викимедиа. 2010.

Полезное

Смотреть что такое «Призма (математика)» в других словарях:

Девять книг математики — (Введение) «Девять книг математики» (китайская традиция. Арифметика Арифметика… Википедия.

ГЕОМЕТРИЯ — это раздел математики, который занимается изучением свойств различных форм (точек, линий, углов, двумерных и трехмерных объектов), их размеров и расположения между ними. Для удобства преподавания геометрия подразделяется на измерение площади и стереометрию. В: …… Энциклопедия Colliers.

Земляков, Александр Николаевич Файл:Земляков.jpg Александр Николаевич Земляков (17 апреля 1950(19500417), Борогое — 1 января 2005, Черноголовка) математик, выдающийся Советский и российский педагог, писатель-педагог … … Википедия.

Александр Николаевич Земляков (17 апреля 1950(1954417), Борогое — 1 января 2005, Черноголовка) — математик, выдающийся советский и российский математик и автор учебной литературы. БиографияВ 1967 году получил золотую медаль. …… Википедия.

Правильный многогранник — додекаэдр Правильный многогранник или платоново тело — это выпуклый многогранник с пространственной симметрией, состоящий из одинаковых правильных многоугольников … Википедия

Пирамида (геометрия) — у этого термина существуют и другие значения. См. Пирамида (понятие). Достоверность этого раздела статьи была оспорена. Фактическая точность этого раздела нуждается в проверке. Страница обсуждения может объяснить… Википедия.

Бипирамида — или двугранник — это трехмерный многогранник, образованный двумя пирамидами, одна из которых является изображением другой. Стыки пирамид образуют общий многоугольник. Простые пирамиды — …… Создано по материалам Википедии

Изогнутый многогранник — Многогранник (точнее, многогранная поверхность) называется изогнутым, если его пространственная форма может быть изменена последовательными временными деформациями так, что каждая грань не меняет своих размеров (т.е. движется как твердое тело) … Википедия

Норма (мыслитель) — «Мыслитель», Огюст Роден философия (от греч. «Любовь мудрости», «Мудрость», Филон «Любовь и мудрость мудрости») Общая теория … Википедия

Пример 3.Ромб с диагоналями 12 и 16 дает прямую призму с основанием. Боковая грань призмы равна 25. Найдите область поверхности призмы.

Что такое призма: определение, элементы, виды, варианты сечения

В данной статье мы рассмотрим определение, основные элементы, типы и возможные вариации поперечного сечения призмы. Представленная информация сопровождается иллюстрациями для лучшего понимания.

Призма — это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными поверхностями (многоугольниками), остальные поверхности — параллелограммы.

На рисунке ниже показан один из наиболее распространенных типов призм — четырехугольник (или параллелепипед). Другие вариации этой формы обсуждаются в последнем разделе данной статьи.

Элементы призмы

Основания – равные многоугольники. Это могут быть треугольники, четырех-, пяти-, шестиугольники и т.д. В нашем случае – это параллелограммы (или прямоугольники) ABCD и A₁B₁c₁d₁ 。

Призма — это разбиение всех граней фигуры на одну плоскость (чаще всего одно из ее оснований). Например, для прямоугольной прямой призмы:

Примечание: свойства призмы представлены в отдельной публикации.

Оранжевый цвет представляет собой основание, а желтый — стороны нашего будущего куба. Предположим теперь, что нам нужно найти площадь боковых сторон. Как мы это делаем?

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, умножьте площадь основания на высоту призмы.

Объем призмы = площадь основания х высота

Площадь боковой поверхности призмы

Чтобы найти площадь сторон треугольной призмы, умножьте периметр основания на высоту.

Площадь сторон треугольной призмы = периметр основания x высота

Площадь полной поверхности призмы

Чтобы найти общую площадь призмы, сложите площадь ее основания и площадь ее боковых сторон.

учитывая, что S_側=P_ベース 。 h, получаем:

Правильная призма — это прямая призма, основанием которой является правильный многоугольник.

Свойства призмы :

Верхнее и нижнее основания призмы являются равными многоугольниками. Стороны призмы имеют форму параллелограмма. Боковые грани призмы параллельны и равны.

Совет: При расчете треугольной призмы будьте внимательны к используемым единицам измерения. Например, если площадь основания дана в см 2, то высота должна быть выражена в сантиметрах, а объем в см 3. Если площадь основания дана в мм 2, то высота должна быть выражена в мм, а объем в мм 3, и т.д.

Пример призмы

В данном примере: — ABC и DEF — треугольные основания призмы — ABED, BCFE и ACFD — прямоугольные боковые грани — Боковые грани DA, EB и FC соответствуют высоте призмы — Точки A, B, C, D, E, F — вершины призмы.

Проблема 1. Основание правильной треугольной призмы — правильный треугольник с вершинами 6 и 8, боковое ребро — 5. Найдите объем призмы. Решение: Объем призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае равна площади прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Следовательно, объем равен:

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковой грани. Объем разрезанной треугольной призмы равен 5. Найдите объем исходной призмы.

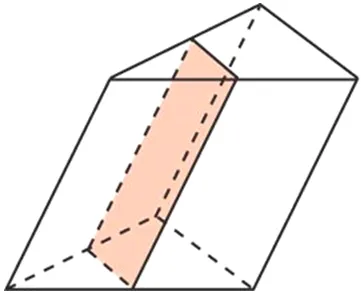
Объем призмы равен произведению площади основания на высоту: V = S_ベース -h.

Треугольник в основании исходной призмы похож на треугольник в основании разрезанной призмы. Коэффициент подобия равен 2, поскольку пересечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего треугольника). Известно, что площади похожих фигур связаны как квадрат коэффициента сходства, т.е. S₂ = S₁k 2 = S₁2 2 = 4S₁。

Площадь основания всей призмы в четыре раза больше площади основания отделенной призмы. Поскольку обе призмы имеют одинаковую высоту, объем целой призмы в четыре раза больше объема усеченной призмы.