Уравнения с дробями можно решать с помощью аналогий или легких решений. Первое уравнение и другие подобные уравнения можно очень легко и быстро решить с помощью коэффициентов. Умножение.
Дроби и все Действия с Дробями
Операции с дробями выполняются во всех школьных математических дисциплинах. Мы редко видим их в жизни, но постоянно слышим и говорим — половина, четвертая, третья. Однако в каждом экзамене есть примеры дробей и операций с ними. Калькуляторы редко помогают в этом. Кроме того, сначала нужно научиться пользоваться такими сложными калькуляторами. Очень часто дробные вычисления встречаются в физике, химии и иногда в биологии. Дроби были изобретены людьми для решения проблемы деления на остатки. 8:2 = 4 (четное, без остатка) и 9:2 = 4, остаток 1.
Деление означает дробление на более мелкие части. А в математике дробь меньше целой единицы. В качестве примера я люблю использовать торт. По какой-то причине студенты находят способ разделить торт на много равных частей. По сути, это применение математики к жизни.
Когда торт разделен на две части, они называются половинками; когда они имеют форму дроби, они называются «секундами».
Цифра 1 над дробью называется ЧИСЛО и указывает на количество (ЧИСЛО) фигур, которые у нас есть. Число, стоящее под двумя дробями, называется ЧИСЛО и указывает количество равных частей, на которые делится множество (например, торт).

Если вы не можете запомнить названия числителя и знаменателя, вам придется посмотреть на них и использовать примеры дробей для определения и практики. Эти слова часто используются в математике, физике и даже в жизни. Вы когда-нибудь слышали о «приведении к общему знаменателю»? Кстати, «принести» в математике не означает «переместить что-то или кого-то в нужное место». Например, «вывести автомобиль на дорогу».
В математике «принести» означает, что я действую в соответствии с правилами. Это позволяет мне получить что-то подобное или похожее на что-то. Другими словами, я убеждаюсь, что знаменатели дробей одинаковы. Попросите их разделить «пирог» (круг) на четыре равные части, восемь частей и три части. Попросите его найти способ сделать части равными.
Когда он разделит его на четыре части, скажите ему, что одна часть называется ЧЕТВЕРТЬ, две такие части — две четверти, а три такие части — три четверти. Дайте ему возможность попрактиковаться в назывании различных дробей, пока он не будет понимать их очень хорошо. Затем задайте вопросы — как вы добавляете одинаковые части? Сколько четвертей и четвертинок? Правильно — две четверти. Другими словами, если вы складываете дроби с одинаковым знаменателем, не трогайте знаменатель, он останется прежним, а добавьте числитель. Если ученики складывают знаменатель (например, одна секунда и одна секунда дают две четверти, что неправильно!) ), попросите их нарисовать рисунок на торте. Спросите его, что он получает от торта и какие части торта он видит, и визуально сравните их. Что он должен получить при их правильном сложении. Затем он должен сложить дроби с разными знаменателями. Если у него возникают проблемы, покажите ему, как это делается, на следующем примере.
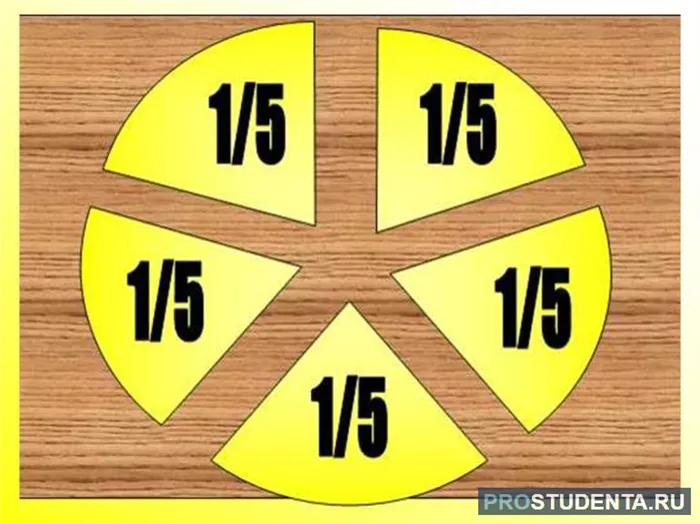
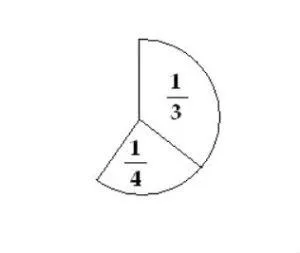
Эти торты имеют разные размеры. Их можно сдвинуть вместе, и мы получим настоящую часть торта: фракцию.
Умножение Дробей
Если ученик легко складывает дроби, переходите к умножению дробей. Здесь необходимо помнить правила.
При умножении дробей числитель умножается на числитель, а знаменатель умножается на знаменатель.
Конечно, вам нужно попрактиковаться в этом действии, пока вы не будете уверены!
Деление Дробей
При делении дробей, конечно, можно делить числитель на числитель и знаменатель на знаменатель. Однако это не всегда срабатывает. Если вы попытаетесь разделить 2 на 3 или 5 на 7 в предыдущем примере, то вряд ли получите что-то практичное. Вот почему это делается.

Вторая дробь инвертируется, и первая дробь умножается на ТРАНСФОРМИРОВАННУЮ вторую дробь.
Это правило необходимо понять и выучить. И, конечно, вы должны практиковать эту энергию, пока не будете уверены!
Рассмотрим пример решения уравнения с дробями. Примеры просты и показательны. Они помогут вам научиться решать дробные уравнения самым наглядным образом. Например, решите простое уравнение x / b + c = d.
Основные свойства дробей
- Дробь является видом записи числа. Одно и то же число можно записать в виде разных дробей.
- Если умножить числитель и знаменатель на одинаковую величину, то значение дроби останется прежним, хотя дроби разные: \(\frac pr=\frac.\) Например, \(\frac34=\frac68=\frac9.\)
- И обратно, если числитель и знаменатель имеют общий делитель, то обе части можно разделить на него. Такая операция называется сокращением дроби : \(\frac=\frac=\frac34.\)
Несократимая дробь — это дробь, числитель и знаменатель которой просты друг к другу. Другими словами, не существует наибольшего общего делителя, отличного от 1 (-1).
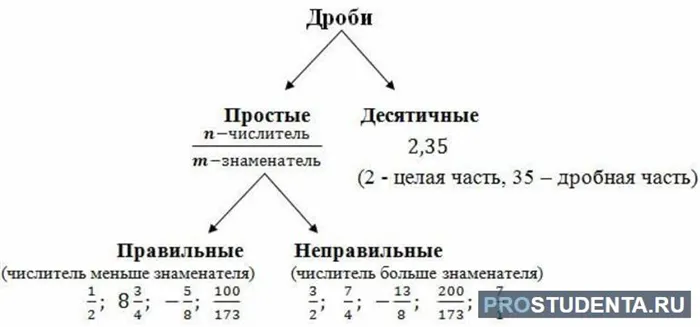
Существует два типа дробей: правильные и неправильные.
Неправильные дроби всегда больше правильных: \(\frac
Правильные дроби
Неправильные дроби — это обычные дроби, у которых числитель меньше знаменателя.
Правильная дробь называется так, поскольку выражает «правильную» часть единицы, то есть часть, которая меньше целого: \( \frac25
Рассмотрим дробь \(\frac56\), у которой 5 — это числитель, а 6 — знаменатель.Сравним числитель со знаменателем: 5
Неправильные дроби
Неправильные дроби — это обычные дроби, у которых числитель больше или равен знаменателю. Эти дроби всегда больше или равны 1: \ (\ frac73> 1, \ frac8> 1, \ frac55 = 1).
\Согласитесь с ᢙᢙ (ᢙ frac65 \). Здесь 6 — числитель, а 5 — знаменатель. Поскольку 6> 5, дробь неверна.
Поэтому, сравнивая дробь с 1, мы можем отличить правильные дроби от неправильных. Это различие не влияет на арифметические операции, но важно при сравнении дробей.
Смешанные дроби
Нередко в результате вычислений остаются неправильные дроби. Рекомендуется перевести их в смешанные числа. Каждая неправильная дробь может быть представлена в виде смешанного числа.
Смешанное число — это число, которое содержит целую часть и дробную часть.
Чтобы создать смешанную фракцию, необходимо следующее
- Выделить наибольшее целое число, содержащееся в неправильной дроби. Для этого нужно разделить числитель на знаменатель. Получившееся частное без остатка является целой частью смешанной дроби: \(\frac5=40:5=8\) .
- Если в результате деления есть остаток, то этот остаток становится числителем дробной части. Знаменатель дробной части останется частным. \(\frac5=8\frac25\)
Опишите неправильную дробь ⌘ (⌘ frac4 \) как смешанную дробь.
Извлеките всю смешанную фракцию. Для этого разделите числитель дроби, 18, на знаменатель, 4. Следовательно, ס(ס frac4 = 18:4 = 4 \) и остаток будет равен 2.
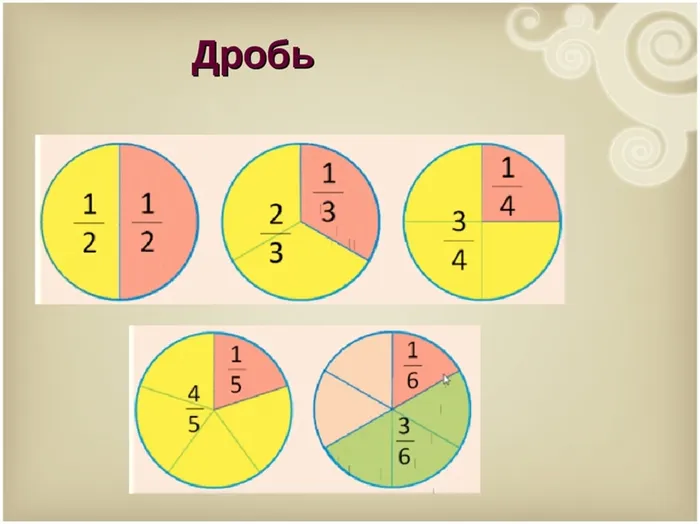
В этом случае требуемая смешанная фракция составляет ⌘ (⌘ frac4 = 4 \ frac24. ⌘). Эту дробь можно уменьшить, разделив числитель и знаменатель дроби на наибольший общий делитель 2.
Смешанные числа могут быть записаны в виде неправильных дробей. Для этого умножьте целую часть на знаменатель дробной части. Добавьте десятичный числитель к полученному числу. Запишите эту сумму в числитель, а десятичный знаменатель оставьте без изменений.
Запишите смешанное число \(6 \ frac25 \) в виде неправильной дроби.
Как перевести правильную дробь в неправильную
Обычные дроби не могут быть преобразованы в неправильные дроби и наоборот. Это разные категории чисел.
Натуральные числа могут быть описаны как неправильные дроби: \(2 = \ frac21. \)
Дробь с числителем p и знаменателем 1 — это еще одна форма записи натурального числа p. Это правило можно выразить следующим уравнением. \ p = \ frac p1.
Число 0 равно дроби вида ⌘ (⌘ frac0q \). где q — любое натуральное число.
Действия с дробями, как решать примеры
Приведение к общему знаменателю
Чтобы решить большинство примеров с дробями, их нужно привести к наименьшему общему знаменателю. Для приведения дробей ⌘ (⌘ frac ab \) и \ (⌘ frac cd \) к общему знаменателю требуется следующее.
- Найти наименьшее общее кратное (НОК) обоих знаменателей: \(M=\leftb,d\right.\)
- Умножить числитель и знаменатель первой дроби на M/b: \(\frac.\)
- Умножить числитель и знаменатель второй дроби на M/d: \(\frac.\)
Вам нужно привести дроби ⌘ (⌘ frac 34 \) и Ᏺ (⌘ frac 13 \) к наименьшему общему знаменателю. Используйте этот алгоритм.
- Находим НОК. У чисел 4 и 3 им является число 12.
- Умножаем числитель и знаменатель первой дроби на \(\frac4\), то есть 3: \(\frac=\frac9\) .
- Умножаем числитель и знаменатель второй дроби на \(\frac3\), то есть 4: \(\frac=\frac4\) .
Сравнение
Чтобы сравнить дроби, нужно привести их к общему знаменателю и сравнить числители. Дробь с наибольшим числителем будет больше.
\ frac34> \ frac13, ⌘) потому что ⌘ (⌘ frac9> \ frac4. ⌘)
При сравнении смешанных чисел сначала необходимо рассмотреть целое. Самыми большими являются числа с большими целыми частями.
Если целое число смесей одинаково, то дробные части сравниваются по обычным правилам сравнения дробей. Максимальное количество дробных частей будет больше: ס(5 \ frac23> 5 \ frac13.ס)
Сложение и вычитание
Чтобы сложить дроби, прибавьте числитель к общему знаменателю, оставив знаменатель неизменным. При необходимости преобразуйте дробь в смешанное число.
При сложении смешанного числа целые и дробные части складываются отдельно.
Если вы хотите отнять одну дробь от другой, вы должны привести их к общему знаменателю, убрать числитель и оставить знаменатель нетронутым.
Умножение и деление
Чтобы умножить дробь, перемножьте числитель и знаменатель.
Умножьте долю \ (\ frac35 \) на \ (\ frac23. \).
При умножении дроби на натуральное число числитель умножается на это число, а знаменатель остается сам по себе. Это потому, что каждое натуральное число можно выразить в виде ⌘ (p = ⌘ frac p1.
)
Чтобы умножить смешанные числа, необходимо сначала выразить их в виде дробей, а затем выполнить математические действия.
Чтобы разделить одну дробь на другую, умножьте первую дробь на обратную дробь. Знаменатель и числитель второй дроби не должны быть равны нулю.
)
\Поделить дробь (⌘ frac34 \) на ⌘ frac23.
При делении смешанных чисел, например, при умножении, необходимо сначала превратить их в дроби.
При решении этого уравнения вы не переносите все на одну сторону и не приводите дроби к общему знаменателю. Обе части уравнения сразу же умножаются на уравнение, которое уменьшает все знаменатели одновременно.
Свойства дробей
Предположим, что часть формы A / B дана. Если числитель и знаменатель умножить на одно и то же число, скажем, на c, результат будет одинаковым: a / b = (a * c) / (b * c). Этот закон называется фундаментальным свойством дробей. Он особенно полезен при дополнениях и удалениях, так как упрощает выражения в простой форме.
Это правило можно доказать следующим образом. Пусть причина A / B равна k. Отсюда числитель можно выразить с помощью кавычек: a = b * k. Это выражение можно умножить на число, не равное нулю. Результат: a * c = (b * k) * c. Правая часть содержит произведение. Поэтому, используя закон счетчика, уравнение можно переписать как A * c = (b * c) * k. Выражение результата k = (a * c) / (b * c). a / b = (a * c) / (b * c). Имущество доказано.

Второе свойство можно сформулировать так: если есть дробь A / B, то изменение знака перед числителем и изменение всей дроби не меняет результата. То есть, a / b = — (- a / b). Это также относится к действиям над знаменателем. Правила следующие. Пусть одно равно: (-a / b) = k. Числитель можно выразить через определение четверти: -a = b * k. Это основание можно умножить на -1. Уравнение становится: a = -b * k. Если -k = a / b → k = K за счет (a / b), необходимо доказать.
При решении некоторых примеров имеет смысл сокращать дроби в том же виде. Для этого действуют следующие правила.

- Чтобы привести смешанную дробь в неправильную нужно целую часть умножить на знаменатель, а потом прибавить к полученному результату числитель. Затем, делитель оставить без изменения, а в числитель записать сумму. Например, 3 (½) = ((3 * 2) + 1) / 2 = 7 / 2.
- Для преобразования неправильного выражения в смешанное нужно выделить из дроби целую часть, а остаток занести в числитель, оставив знаменатель без изменения. Для нахождения целого можно воспользоваться правилом деления в столбик. Например, 18 / 5 = 3 (3/5).
Стоит отметить сингулярность смешанных дробей. Символизм вида c(a / b) означает, что между интегралом и дискурсом существует положительный символизм. Другими словами, c(a / b) = c + (a / b) на практике.
Усвоив правила, вы можете изучить математические алгоритмы для сложения и удаления дробей.
Правила действий

Чтобы научиться быстро складывать и вычитать дроби, необходимо понять правила приведения к общему знаменателю. Если вам нужно отредактировать выражение с разными делителями, необходимо выполнить преобразование. Например, предположим, что у вас есть дробь 3 /5. Согласно основному свойству, вы можете умножить числитель и знаменатель на одно и то же число. Таким образом, мы можем написать: 3/5 = (3 * 8)/40 = 24/4/4. Другими словами, числитель увеличивается на коэффициент, равный числу, на которое изменяется знаменатель.
Таким образом, если есть две дроби с разными знаменателями, то для нахождения общего числа нужно найти минимальное число, деленное на единицу, если нет остатка, и на другой знаменатель. На самом деле, это наименее распространенное кратное число. Его можно найти, выполнив следующую серию функций.
- разложить каждый знаменатель на множители;
- из полученного ряда убрать повторяющиеся цифры;
- найти произведение оставшихся чисел, которое и будет искомым общим знаменателем.
Таким образом, существует два случая, когда можно получить дополнительные вычеты. Первый вариант очень прост, а второй является особым случаем. Для лучшего понимания полезно записать алгоритм для каждого случая в виде таблицы.
- Сложить или вычесть делимые.
- Результат записать в числитель, а знаменатель переписать без изменения.
- (a / b) + (c / b) = (a + c) / b;
- (a / b) — (c / b) = (a — c) / b.
- Привести дроби к общему знаменателю (НОЗ).
- Найти дополнительные множители для числителей путём деления НОЗ на знаменатель каждой дроби.
- Выполнить умножение.
- В числитель записать сумму или разность, а в знаменатель — НОЗ.
- (a / с) + (m / b) = (a * b + m * c) / (c * b);
- (a / с) — (m / b) = (a * b — m * c) / (c * b).
Следует отметить, что действия с использованием смешанных фракций не отличаются от описанных выше. Единственное, действия с целыми числами выполняются отдельно от дробных и записываются общие эффекты.
Примеры решений
Подробные объяснения примеров дробей в 5 классе помогают учащимся лучше понять теоретические вопросы. В то же время полученный опыт позволяет им самостоятельно решать сложные задачи. Это типичные проблемы, используемые в контексте обучения учеников в средней школе.

- Найти результат действия: 3 / 14 + 10 / 21. Дроби в выражении имеют разные знаменатели. Согласно алгоритму, их нужно привести к общему знаменателю, а затем с его помощью найти дополнительные множители. Для этого 14 и 42 следует разложить на простые числа: 14 = 2 * 7; 42 = 2 * 3 * 7. Отсюда следует, что НОЗ = 2 * 7 * 3 = 42. Далее, всё по алгоритму: ((3* 3) / 42) + ((2 * 10) / 42) = (9 / 42) + (20 / 42) = (9 + 20) / 42 = 29 / 42.
- Определить разность: 26 / 40 — 9 / 25. Пример решается аналогично предыдущему, но перед поиском НОЗ, первый член можно упростить. Для этого числитель и знаменатель нужно разделить на два: 26 / 40 = 13 / 20. Придерживаясь последовательности действий решение можно записать так: 13 / 20 — 9 / 25 = ((13 * 5) / 100) — ((9 * 4) / 100) = (65 — 36) / 100 = 29 / 100.
- Вычислить ответ: 3 (5/8) — 1 (9/10). В этом случае удобно целые части вычесть отдельно от дробных. Тогда, решение будет выполнено за два действия. Первое 3 — 1 = 2. Второе (5 / 8) — (9 / 10) = ((5 * 5) / 40) — ((4 * 9) / 40) = (25 — 36) / 40 = — 11 / 40. Таким образом, ответ будет: 2 (-11/40). Такая запись некорректная, поэтому из целого нужно вычесть дробное выражение. В итоге получится: (2 / 1) — (11 / 40) = (80 — 11) / 40 = 69 / 40 = 1 (29 / 40).
- Найти результат действия: 1 (2/5) + 4 / 5. В этом случае смешанное число удобно перевести в неправильную дробь, а уже после, выполнить сложение. Так, 1 (2/5) = ((1 * 5) + 2) / 6 = 7 / 5. Теперь получились две дроби с одинаковым знаменателем. Воспользовавшись алгоритмом из таблицы, найти их сумму будет несложно: 7 / 5 + 4 / 5 = (7 + 4) / 5 = 11 /5 = 2 (1/5).
Следует отметить, что последний пример можно решить без преобразования смешанных дробей в неправильные. Уравнение можно записать в виде 1 (2/5) + 4/5 = 1/1 + 2/5 + 4/5, а ответ можно вычислить в два этапа. Основной разницы в использовании нет, но, пожалуй, первое отличие — удобнее и быстрее; второе отличие — вы можете использовать одну и ту же формулу двумя разными способами.








