Интересно!!! Квадратный многочлен называется многочленом из-за его высоты, квадрата. Три наименования называются многочленами из-за их суммы.
Как разложить на множители квадратный трехчлен: формула
Разбиение полиномов для получения продукта может показаться запутанным. Однако это не так сложно, если вы понимаете пошаговый процесс. В этой статье подробно описано, как анализировать квадрат 3 множителя.
Многие люди не понимают, как анализировать квадратные трехчлены с множителями и зачем это делается. Сначала это может показаться бесполезным занятием. Однако в математике это делается не просто так. Преобразования выполняются для того, чтобы упростить уравнение и облегчить его вычисление.
Многочлен в форме -Ax²+Bx+C- называется квадратным трехчленом. Сумма ‘a’ должна быть отрицательной или положительной. На практике это уравнение называется квадратным уравнением. Поэтому иногда говорят по-другому: как разложить квадратное уравнение.
Интересно! Многочлен называется квадратным многочленом из-за его высоты, квадрата. Загрузку называют полиномом, потому что она состоит из трех компонентов.
Другие типы полиномов:.
Разложение квадратного трехчлена на множители
Сначала уравнение должно быть равно нулю, затем нужно найти скорость корней x1 и x2. Корней может не быть, может быть один или два корня. Наличие корней определяется по усмотрению. Должен быть известен внешний тип: d =b²-4ac.
Если эффект D отрицательный, то корней нет. Если результат положительный, то корней два. Если результат равен нулю, то корень один. Корни также рассчитываются по формуле.
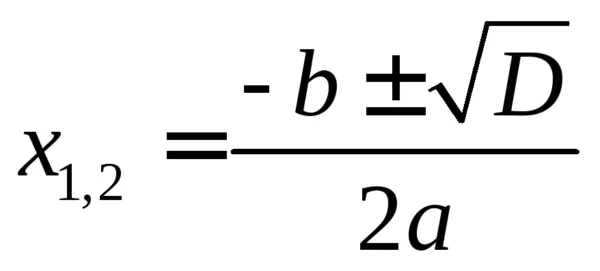
Если расчет тонких способностей дает ноль, можно применить любой тип. На практике человек просто сокращается: -b / 2a.
Разные типы значений тонких способностей различны.

Если формула отрицательная, то вычислять не нужно.
Это интересно! Как найти и что такое окружность круга
Онлайн калькуляторы
В Интернете есть электронные калькуляторы. Их можно использовать для выполнения мультипликативных разложений. На некоторых ресурсах можно найти пошаговые решения. Такие услуги могут помочь вам лучше понять предмет, но вы сами должны постараться понять его лучше.
Если тема ясна, рекомендуется проверить решение с помощью электронного калькулятора.
Полезное видео: Разложение квадратного трехчлена на множители
Целесообразно рассмотреть простой пример анализа квадратного уравнения множителя.
Пример 1

Здесь очевидно, что результат равен 2 x, так как d положительно. Их необходимо заменить прессом. Если корень отрицательный, сигналы пресса меняются на противоположные.
Читайте также: Самая высокая гора в Австралии: чтобы взобраться на нее, не обязательно быть альпинистом
Тип расширения квадратного тринома: a (x-x1) (x-x2) известен. Заключите значения в скобки: (x+3) (x+2/3). Нет числа, предшествующего сумме оценок. Это значит, что он есть, опущен.
Это интересно! Как определить модуль действительного числа и что это такое
Пример 2

Этот пример наглядно показывает, как решить уравнение с корнями.
Замените полученное значение.
Пример 3
Как и в предыдущем случае, сначала вычислите дискретные мощности.
Поскольку дискриминант отрицательный, корень не существует.
После получения результата стоит открыть скобу, чтобы проверить результат. Должен появиться оригинальный трехколесный велосипед.
Если общий фактор поместить за скобку, то получится произведение двух факторов: один — заданный, другой — очень важный. Например:.
Примеры с решением квадратного уравнения
Пример 1.1
Уберите множитель из многочлена: x 4 + x 3-6 x 2.
Установите x 2 из кронштейна:. Решите квадратное уравнение x 2 + x -6 = 0:. Корни уравнения:.
Таким образом, мы получаем развитие полинома в множителе.
Пример 1.2
Произведите факторизацию и анализ кубического многочлена x3+ 6 x 2 +9x.
Удалите x из скобок:. Решите квадратное уравнение x2+ 6 x + 9=0. Разница заключается в следующем. Корни уравнения кратны, так как дискриминант равен нулю. .
Таким образом, мы получаем развитие полинома в множителе.
Пример 1.3
Факторизуйте пятисильный многочлен: x 5-2 x 4 + 10×3.
Снимите x3 с кронштейнов:. Решите квадратное уравнение x2-2x + 10=0. Решение заключается в следующем. Корни уравнения являются комплексными, так как дискриминант меньше нуля. ,.
Разложение полинома на коэффициенты выглядит следующим образом
Если вы заинтересованы в разработке множителя с действительными коэффициентами
Примеры разложения многочленов на множители с помощью формул
Примеры с биквадратными многочленами
Пример 2.1
Разложите двоичный многочлен на множители: x 4 +x2-20.
Примените следующее уравнение: a2+2 ab + b 2 = (a + b)2; a 2-b 2 = (a -b) (a + b). ; .
Пример 2.2
Разложите сокращенный многочлен на двоичные многочлены: x 8 + x 4+1.
Примените следующее уравнение: a2+2 ab + b 2 = (a + b)2; a 2-b 2 = (a —b) (a + b): ;.
Пример 2.3 с возвратным многочленом
Разложите возвращаемый многочлен на коэффициенты.
Многочлен имеет ненужную степень. Следовательно, корень x = -1. Разделите многочлен на x- (-1) = x+1. Результат следующий. Обмен:, ; ; ; ; ; .
Примеры разложения многочленов на множители с целыми корнями
Пример 3.1
Анализирует многочлен множителя.
Предположим, что уравнение имеет хотя бы один целочисленный корень. Тогда оно является делителем числа 6 (член без x). Это означает, что целочисленный корень может быть одним из чисел -6, -3, -2, -1, 1, 2, 3 или 6. Замените эти значения по одному: (-6) 3-6-(-6)2 + 11-(-6)-6 = -504; (-3) 3-6-(-3)2 + 11-(-3)-6 = -120; (-2) 3-6-(-2)2 + 11-(-2)-6 = -60; (-1) 3-6-(-1)2 + 11-(-1)-6 = -24; 1 3-6-1 2 + 11-1- 6 = 0; 2 3-6-2 2 + 11-2-6 = 0; 3 3-6-32 + 11-3—6 = 0; 6 3-6-6 2 + 11-6-6 = 60.
Таким образом, найдены три корня: x1 = 1, x2 = 2, x3 = 3. Исходный многочлен является кубическим и поэтому имеет не более трех корней. Если найдены три корня, то они являются первыми. Итак
Пример 3.2
Анализирует многочлен множителя.
Предположим, что уравнение имеет хотя бы один полный корень. Тогда оно является делителем числа 2 (член без x). Это означает, что корнем из целого числа может быть число -2, -1, 1 или 2. Заменяем эти значения по одному: (-2) 4 + 2-(-2) 3 + 3-(-2) 3 + 4-(-2) + 2 = 6; (-1) 4 + 2-(-1) 3 + 3-(-1) 3 + 4-(-1) + 2 = 0; 1 4 + 2-1 3 + 3-1 3 + 4-1 + 2 = 12; 2 4 + 2-2 3 + 3-2 3 + 4-2 + 2 = 54.

Общие множители также могут быть многочленами в скобках.

При выполнении задания «умножить-делить» следует обратить особое внимание на символы при вынесении общих множителей за скобки. Чтобы изменить знак каждого члена в скобках (b —a), поместите общий множитель -1 после скобок, и каждый член в скобках делится на -1: (b —a) = -(a —b).

Если выражение в скобках является квадратом (или любой четной степенью), то минус в скобках все равно преобразуется, поэтому числа в скобках можно поменять местами: (b —a)2 = (a —b)2, (b- a)4 = (a —b)4 и т.д….
3. Способ группировки
Не все итоги в выражении имеют общий элемент, а только некоторые из них. Затем суммы в скобках группируются таким образом, чтобы из каждой из них можно было получить один множитель. Метод группировки заключается в том, что из квадратных скобок дважды удаляется общий множитель.

Чтобы открыть хранилище, необходимо ввести код. Он состоит из первых пяти чисел, записанных в порядке убывания. Все эти числа являются 984 простыми числами.
Что такое множитель и разложение на простые множители
Определите термин «мультипликатор» и поймите, что такое мультипликатор. Какие существуют множители и почему некоторые множители стоят на первом месте.
В средней школе нас учили, что множители — это числа, которые мы умножаем, а результат умножения мы называем произведением.

Определение множителя как компонента умножения
Давайте теперь немного расширим понятие мультипликатора.
Множитель — это число или формула, участвующая в представлении числа или формулы в виде произведения.
Представление числа или выражения в виде произведения чисел или выражений — это деление на множители.
Давайте рассмотрим определение множителя на примере. Определите, где спрятан множитель в представлении числа или выражения.
Пример 1
Предположим, вам дано число 15. Это число можно выразить как его произведение. Поэтому, по определению, 5 является множителем, и 3 также является множителем.
Пример 2
Теперь рассмотрим следующее уравнение. Это выражение можно выразить как произведение. Первый множитель (2x — 3) и второй (2x + 3) дают два множителя.
Простейший продукт имеет два множителя, но множителей может быть и больше.
Простые множители
Если число может быть выражено либо само по себе, либо как произведение чисел, кратных единице, то такие числа называются простыми множителями. Другими словами, простой фактор — это простой делитель числа, которое не делится на остаток.
Пример 1
Разделите число 65 на простые множители.
Решение: разделите 65 на простые числа, пока они не будут делиться поровну. Таким образом, мы видим, что число 65 не делится на 2, 3 и 4, потому что оно не удовлетворяет делителю этих чисел. Однако оно делится на 5, потому что оканчивается на 5. Деление дает 13, которое является простым числом, так как число 13 делится только на себя и на 1. Следовательно, число. Таким образом, мы завершили разработку числа простых факторов. Теперь мы знаем, как проанализировать количество простых факторов.
Пример 2
Мы анализируем число 270 в простой факторизации.
Решение: сначала проверьте, равно ли число 270 2 (сначала получите наименьшее первое число) и получите 135. Проверьте, делится ли это число на 3. Для этого нужно сложить все числа с таким количеством чисел — число 135 делится на 3: ведь девятка делится на 3. Полученное число снова делится на 3:. Опять же, число 15 делится на 3:. Получено первое число 5. Отдельно.
Запишите первый коэффициент 270 в виде столбца. Теперь разделите первое число и запишите то, что получилось, в правой части ряда, записанного в левой части.
Чтобы проверить, что исходное выражение является кубом суммы двух выражений, нужно выяснить, что в данном случае является переменной A, а что переменной b.
Формулы умножения
Во многих случаях для упрощения вычислений используются сокращенные виды умножения. Всего существует семь представлений, которые необходимо изучить. Вы можете найти их в таблице в учебнике алгебры седьмого класса. Значения этих теорий следующие

- Разность двух членов, стоящих во второй степени, прямо пропорциональна произведению разности этих членов на их сумму. Например, 16 2 — 3 2 = (16 — 3) * (16 + 3) = 247 или 9 * h 2 — 4 * e 2 * h 2 = (3 * h — 2 * e * h) * (3 * h — 2 * e * h).
- Квадрат суммы двух членов можно разложить на квадрат первого элемента и удвоенное произведение его на второй элемент, прибавив квадрат второго члена. Используя это правило, можно быстро находить квадрат числа без использования калькулятора. Например, 114 2 = (100 +14) = 100 2 + 2 * 100 * 14 + 14 2 = 10000 + 2800 + 196 = 12966.
- Квадрат разности двух членов равняется квадрату первого члена с вычетом из него двойного произведения первого на второй с добавлением квадрата второго члена. В этом правиле используют обыкновенное раскрытие скобок. Например, (6 — 3) 2 = 6 2 — 2 * 6 * 3 + 3 2 = (3 — 6) 2 = 9 .
- Кубическая сумма двух выражений определяется кубом первого члена с прибавлением к нему утроенного произведения исходного числа в степени два на второй член, плюс увеличенное в три раза произведение исходного числа на квадрат второго с прибавлением этого элемента в третьей степени. Например, (2h+7e) 3 = (2 * h) 3 + 3 * 2 * h 2 * 7* e + 3 * 2h * (7 * e) 2 + (7 * e) 3.
- Куб разности находится вычитанием из исходного числа утроенного произведения первого члена, возведённого во вторую степень, с прибавлением утроенного произведения исходного члена на второй в степени два минус его куб. Например, (4 * h − 2 * e) 3 = (4 * h) 3 − 3 * (4 * h) 2 * 2 * e + 3 * 4 * h * (2 * e) 2 − (2 * e) 3 .
- Сумма кубов находится как произведение суммы членов на неполный квадрат разности: (5 * h) 3 + 8 3 = (5 * h + 8) * ((5 * h) 2 − 5 * h * 8 + 8 2). Неполным квадратом называют выражение: (h 2 — h * e + e 2).
- Разность кубов равна выражению, полученному перемножением разности двух чисел на неполный квадрат суммы: h3− e3 = (h − e) * ((h 2 +h) * (e + e 2)).
Все эти виды умножения можно использовать и в обратном порядке, то есть для составления многочленов. Например, решить следующий пример: «Квадрат 3 анализируется на множители». найти следующее. Как только вы поймете важность этих типов, вам будет очень легко запомнить их со стороны.
Метод группировки
Это, пожалуй, самый распространенный метод умножения. Он полезен для упрощения квадратных уравнений без поиска корней. Разложение по этому методу осуществляется в виде следующей серии шагов.

- выбирают повторяющиеся неизвестные и записывают друг за другом одночлены с одинаковыми множителями;
- в каждой группе находят одинаковый множитель и переносят его за скобку;
- находят общий полином и отделяют его скобками.
Группировка может быть выполнена различными способами, но в конечном итоге требует общего полиномиального уравнения. Например, выражение 48 * h * e 2 + 32 * h * q -15 * e 2-10 * q2 может быть решено двумя способами.
- Изучив выражение, можно заметить, что во всех членах уравнения повторяются две неизвестные. Выписав их друг за другом, а затем вынеся общий множитель за скобку, можно будет записать: 48 * h * e2 + 15 * e2 + 32 * h * q2 − 1 0 * q2 − 10 * q2 = 3 * e2 (16 * h − 5) + 2 q2 (16 * h — 5) = (16 * h − 5) * (3 * e2 + 2 * q2).
- Во втором способе можно использовать то, что в первых одночленах повторяется неизвестная h. Вынеся её за скобку, получают следующее упрощение: 48 * r * z2 + 32 * r * y2 − 15 * z2 − 10 * y2 = 16 * h * (3 * e2 + 2 q2) − 5 (3 * e2 + 2 q2) = (3 * e2 + 2 * q2) * (16 * h − 5).
Чтобы вывести многочлен из скобок, может потребоваться перевернуть все знаки. Помните, что знак минус всех оставшихся мономинов под скобкой будет обратным.
Выделение квадрата
По сути, экспорт общей площади соответствует преобразованию, при котором стволы представляются как (k + e)2 или (k -e)2. Этот метод используется для решения двойных уравнений. При анализе полиномов используются два типа.
Например, дроби нужно упростить: (k4 + 4 * e4) / (k4 + 2 * e2 + 2 * k * e). Числитель необходимо проанализировать с помощью полного квадратного уравнения: (k4 + 4 * e4) = (k4 + 4 * e2 * k2 + 4 * e 4). Поэтому, убрав из многочлена 4 * k2 * e2, получаем уравнение: (k2 + 2 * e2) * 2-4 * k2 * e2. Используя квадратичный вид умножения, правильно написать: (k2 + 2 e 2-2 * k * e) * (k2 + 2 e 2 + 2 * k * e).

Заменив числитель выражением результата, его части можно взаимно сократить в знаменателе. В результате получается простое выражение: h2 + 2 * e2-2 * h * e.








