При вычислении примеров необходимо соблюдать порядок выполнения определенных операций. С помощью следующих правил вы поймете, в каком порядке выполняются действия и зачем нужны скобки.
Памятка по математике » Порядок выполнения действий» ( 3 класс )
Следует отметить, что в соответствии с Федеральным законом n 273-ФЗ «Об образовании в Российской Федерации» и «Об образовании в Российской Федерации» организации, осуществляющие образовательную деятельность, обучение и воспитание обучающихся с ограниченными возможностями здоровья организуют как других обучающихся, так и отдельные классы или группы.
Процедура.
1. если формула содержит только добавления и удаления, выполняйте действия в том порядке, в котором они записаны: слева направо.
… + … — … + … — … — … + …
2. если выражение содержит только умножение и деление, то действия выполняются в порядке записи слева направо.
1 2 3 4 5
… ∙ … : … ∙ …. ∙… : …
Если выражение содержит не только сложения и удаления, но и умножения и деления, или и то и другое, то умножайте слева направо и делите, затем прибавляйте и отнимайте.
… + … ∙ … — … + … : …. ∙… — …
4. если выражение содержит скобки, то скобки после сначала добавляются, а затем удаляются по порядку (слева направо).
… + … — (… — … ) + … — … + (…) : … )
Сначала выполните брекетинг, затем последовательно умножайте и делите
… : … ∙ (… — … ) : … ∙… … + …)
5. после добавления и удаления скобок, сложения и удаления, умножения и деления, первой скобки, умножения и деления после (слева направо), порядок (слева направо) к выражению.
… ∙ (… + …) — … : ( … — …) + …

Курсы переподготовки
Профессиональные компетенции педагога в рамках Федерального закона «Об образовании в Российской Федерации» №273-ФЗ от 29.12.2012

Курсы переподготовки
Теория и методика педагогического проектирования

Курсы переподготовки
Практические аспекты применения современных технологий при обучении школьников математике в рамках ФГОС ООО

«Домашнее обучение. Лайфхаки для родителей»
Краткое описание документа:
Брошюра основана на учебнике «Математика» для 3 класса. Для общеобразовательных организаций. 2 часа. Часть 1 / (М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.) — 6-е изд.
‘Очень разные дети: преимущества статуса учителя для учителей’.
Сертификаты и скидки для каждого участника.
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 913 924 Материал в базе данных.
Материал подходит для УМК
Математика (2 части)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Серия «Исполнение».
‘Интеграция современного искусства в детское творчество’.
Сертификаты и скидки для каждого участника.
Команда ‘Infowalk’ ищет преподавателей.
Другие материалы
- Учебник: «Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Тема: Порядок выполнения действий
- Учебник: «Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Тема: Порядок выполнения действий
- Учебник: «Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Тема: Порядок выполнения действий
- Учебник: «Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Тема: Порядок выполнения действий
- Учебник: «Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Тема: Порядок выполнения действий
- Учебник: «Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Тема: Порядок выполнения действий
- Учебник: «Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Тема: Порядок выполнения действий
- Учебник: «Математика (в 2 частях)», Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Тема: Порядок выполнения действий
‘Практический подход к решению проблемы потери смысла жизни: логопедия’
Сертификаты и скидки для каждого участника.
Вам будут интересны эти курсы:
- Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
- Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
- Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
- Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
- Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
- Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
- Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
- Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
- Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
- Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
- Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
- Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
- Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
- Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Немного потренировавшись в дальнейшем, вы сможете выполнять все действия в цепочке (одно или несколько) и продолжать исходное выражение. В нашем случае мы имеем
Порядок действий
Чтобы правильно вычислить значение числового выражения, требующего нескольких действий, необходимо знать установленный порядок арифметических операций.
Установленный порядок арифметических действий без скобок:.
-
Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
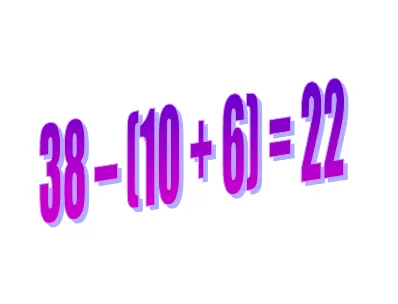
Порядок действий со скобками
Если выражение содержит скобки, то сначала выполняются все действия в скобках, а затем все действия за скобками.
В арифметическом выражении со скобками порядок арифметических действий такой же, как и в выражении без скобок.

Родитель используется для объявления действия, которое должно быть выполнено раньше других. Круглые скобки не влияют на порядок других действий в выражении. Другие действия выполняются в этом порядке.
Дробная черта
Десятичная черта в выражении может быть заменена знаком деления, поэтому все, что выше и ниже десятичной черты, должно быть заключено в скобки. Например:.
| 13 + 2 | = (13 + 2) : (10 — 7). |
| 10 — 7 |
Знак деления в выражении может быть заменен десятичной чертой только в том случае, если не нарушена последовательность операций. Например, следующее выражение.
Замена выражения знаком разделения не допускается, поскольку такая замена нарушила бы последовательность выразительных действий.
| 20 : 4(2 + 3) ≠ | 20 | ; |
| 4(2 + 3) |
| 20 | = 20 : (4(2 + 3)). |
| 4(2 + 3) |
Вертикальная линия в выражении заменяет скобки, это означает, что выражения числителя и знаменателя должны быть вычислены отдельно, и первый результат должен быть разделен на второй результат.
В простом примере все эти функции могут выполняться в вашей голове. Главное — сначала выполнить операции в скобках, запомнить результаты, а затем пересчитать их по порядку слева направо.
Порядок выполнения арифметических действий в выражениях без скобок
Изучите правила выполнения арифметических операций над выражениями без скобок.
Если выражение без круглых скобок содержит только сложение и вычитание или только умножение и деление, выполните действия в описанном порядке.
Выражение содержит только операции сложения и вычитания. Эти операции называются операциями первого этапа.
Задания выполняются в порядке слева направо (рис. 2).
Рассмотрим второе выражение
Это выражение содержит только операции умножения и деления второго шага.
Выполняйте задания в порядке слева направо (рис. 3).
Если выражение содержит сложение и вычитание, а также умножение и деление, в каком порядке выполняются арифметические действия?
Если выражение без скобок содержит не только сложение и вычитание, но и умножение и деление, или и то и другое, то слева направо сначала умножение и деление, затем сложение и вычитание.
Это обосновывается следующим образом. Эта формула включает операции сложения и вычитания, умножения и деления. В соответствии с правилами. Сначала, слева направо, выполняются умножение и деление, затем сложение и вычитание. Исследует последовательность функций.
Вычислите значение выражения.
Порядок выполнения арифметических действий в выражениях со скобками
Если выражение содержит круглые скобки, в каком порядке выполняются арифметические действия?
Если выражение содержит круглые скобки, то сначала вычисляется значение выражения внутри круглых скобок.
Вы видите, что в этом выражении энергия заключена в круглые скобки. Поэтому сначала выполните эту энергию, а затем умножение и сложение. Установите порядок следования функций.
Вычислите значение выражения.
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно думать об определении правильного порядка арифметических действий в арифметическом выражении?
Перед началом вычисления необходимо проверить выражение (посмотреть, содержит ли оно круглые скобки и какие действия содержит) и выполнять действия только в следующем порядке
1. действия в скобках, 2. действия в скобках, 3. действия в скобках, 4. действия в скобках, 5.
Эта диаграмма поможет напомнить вам это простое правило (рис. 4).
Брошюра основана на учебнике «Математика» для 3 класса. Для общеобразовательных организаций. 2 часа. Часть 1 / (М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.) — 6-е изд.
Как правильно решить пример
При вычислении примеров необходимо соблюдать порядок выполнения определенных операций. С помощью следующих правил вы поймете, в каком порядке выполняются действия и зачем нужны скобки.
- сначала выполняем слева направо все действия умножения и деления
- а потом слева направо все действия сложения и вычитания
Рассмотрим следующий пример последовательности действий.
Напомним, что математическая последовательность действий — слева направо (от начала примера к концу). При вычислении значения выражения его можно записать двумя способами.
Первый способ
- Каждое действие записывается отдельно со своим номером под примером.
- После выполнения последнего действия ответ обязательно записывается в исходный пример.
Если вы хотите вычислить результат действия в виде двух- и/или трехзначного числа, обязательно запишите вычисления в столбцах.
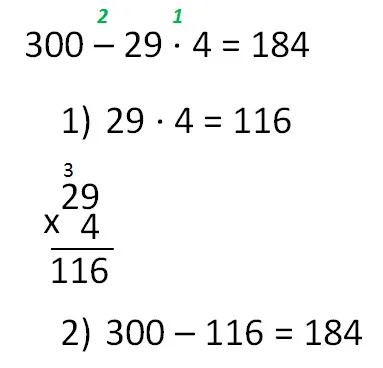
Второй способ
Второй метод известен как «цепное письмо». Все вычисления производятся в точно таком же порядке, но результат записывается сразу после знака равенства.
Если в выражении есть скобки
Если выражение содержит скобки, то сначала выполняется действие в скобках.
В самих скобках правила порядка действий применяются к выражениям без скобок.
Если скобка содержит другие скобки, то сначала выполняется действие внутри скобки.
К сожалению, если вы учите своего ребенка. Примеры 6:2*(1+2) и 6/2*(1+2) идентичны … Незначительно, одна верхняя и одна нижняя точка усредняют разные действия или определяют порядок операций. В этом случае также следует учитывать правило раскрытия скобок: 6: 2*(1+2) = 6: (2*1+2*2) = 6: (2+4) = 6: 6 = 1 — единственный правильный ответ.
Порядок действий. Правила и примеры
Рассмотрим три примера. В каждом из них порядок действий отмечен красной цифрой:.
Вы видите, что, несмотря на одинаковые цифры и знаки, порядок действий в каждом примере разный. Это связано с тем, что во втором и третьем примерах есть круглые скобки.
- Если в примере нет скобок, мы выполняем все действия по порядку, слева направо.
- Если в примере есть скобки, то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.
*Это правило для примеров без умножения и деления. Мы рассмотрим правила для примеров со скобками при умножении и делении во второй части этой статьи.
Чтобы не запутаться в примерах со скобками, можно превратить их в обычные примеры без скобок. Для этого запишите полученный результат в скобках над скобками, перепишите результат на место скобок, выполните все действия слева направо, а затем выполните все следующие действия.
В простом примере все эти функции могут выполняться в вашей голове. Главное — сначала выполнить операции в скобках, запомнить результаты, а затем пересчитать их по порядку слева направо.
Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь посмотрите пример, где добавления и удаления сопровождаются распространением и разделением.
Сначала рассмотрим пример без скобок.
- Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо.
- Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
Чтобы избежать путаницы при решении примеров классов, есть один прием. Если скобок нет, перепишите пример, выполнив действия умножения и деления и записав результат вместо этих действий. Затем последовательно выполните действия по добавлению и удалению.
Если в примере есть скобки, сначала удалите их. Перепишите пример, написав результат вместо скобок. Далее необходимо мысленно выделить части примера, разделенные знаками «+» и «символ», и измерить каждую часть отдельно. Затем добавляйте и удаляйте их по порядку.
Примеры, в которых много действий
Если пример содержит много действий, удобнее выделить блоки и решить каждый блок по отдельности, а не организовывать порядок действий по всему примеру. Для этого найдите свободные символы ‘+’ и » (свободные — это значит, что они не заключены в скобки, как показывают стрелки на рисунке).
Эти символы делят наш пример на блоки.
Помните о том, что при выполнении действий в каждом блоке необходимо соблюдать порядок, указанный выше в статье. После разрешения каждого блока выполните операции добавления и удаления по порядку.
Второй метод известен как «цепное письмо». Все вычисления производятся в точно таком же порядке, но результат записывается сразу после знака равенства.
Порядок действий в математике
В данной публикации рассматриваются математические соглашения, касающиеся порядка выполнения арифметических операций, в частности, представления, включая скобки, экспоненту и абстракцию, а также используется несколько примеров для облегчения их понимания.
Обратите внимание, что с самого начала действия рассматриваются от начала примера к концу, т.е. слева направо.
Общее правило
Сначала он выполняет умножение и деление, затем сложение и вычитание промежуточных значений результата.
Рассмотрим пример более подробно.
Над каждым действием мы написали номер, соответствующий порядку их выполнения. Таким образом, пример решения состоит из трех промежуточных действий.
Немного потренировавшись в дальнейшем, вы сможете выполнять все действия в цепочке (одно или несколько) и продолжать исходное выражение. В нашем случае мы имеем
Если в ряду есть несколько операций умножения и деления, они также выполняются подряд и могут быть объединены при необходимости.
- 5 ⋅ 6 : 3 = 10 (совместное выполнение действий 1 и 2)
- 18 : 9 = 2
- 7 + 10 = 17
- 17 – 2 = 15
Примеры со скобками
Действия в скобках (если они есть) выполняются первыми. Затем внутри них применяется тот же допустимый порядок, что и выше.
Решения могут быть проанализированы в следующих действиях.
- 7 ⋅ 4 = 28
- 28 – 16 = 12
- 15 : 3 = 5
- 9 : 3 = 3
- 5 + 12 = 17
- 17 – 3 = 14
При упорядочивании действий выражения в скобках можно условно считать целыми числами/числами. Для удобства они выделены зеленым цветом в следующей цепочке
Квадратные скобки
Внутри круглых скобок может быть еще один набор скобок (так называемые вложенные скобки). В таких случаях действие сначала выполняется во внутренней скобе.
Расположение примеров в цепочке следующее








