Учитель задавал много вопросов: В чем разница между отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? В чем разница между этими двумя понятиями? «биссектриса угла» и «биссектриса треугольника»? Помогите, пожалуйста, понять и ответить на них. Спасибо
ПОМОГИТЕ ПОЖАЛУЙСТА. СРОЧНО НУЖНО Билет № 1. Какой отрезок называется биссектрисой треугольника?
Сколько биссектрис имеет треугольник? В чем разница между этими двумя понятиями ?».биссектриса угла» и «биссектриса треугольника» ? Объясните с помощью рисунка. 2. сформулировать и докажите первый признак равенства треугольников. 3. рабочий лист № 2 1. какой. отрезок называется высотой треугольника? Сколько высот имеет треугольник? Сделайте рисунок. 2. докажите, что внешний угол треугольника равен сумме двух углов не смежных с ним. 3. Задача Билет №31. Дайте определение окружности. Что такое центр, радиус, это хорда и диаметр круга. Какова взаимосвязь между радиус а диаметр окружности? Сделайте фигуру. 2. доказать вторичную характеристику равенства треугольников. 3. примечание к заданию №41. какова вторичная цель? Что такое пары? углов, образованный пересечением двух линий со вторичной линией. Сделайте фотографию. 2. Продемонстрируйте, что режущий материал по сравнению с… угла при 30* составляет половину. гипотенузы. 3. проблемный лист №51. теорема называется обратной данной теореме? Приведите примеры теорем, обратная величина данных. 2. сформулировать и докажите признак равенства прямоугольных треугольников по гипотенузе и острому углу. 3. Задача какой отрезок называется высотой треугольника
Билет №1 Биссектриса — отрезок, который делит угол на две равный части В треугольнике может быть только 3 биссектрисы (так как 3 угла) Билет#2 Окружность — замкнутая кривая, все точки. которой равноудалены от центральной точки Радиус — отрезок, соединяющий центр окружности, с какой-это его точки Диаметр — отрезок, проходящий через центр окружности от одной точки окружности другой Хорда — отрезок, Соединение двух точек окружности Диаметр равен двойному радиусу (так они связаны)

Если вы не нашли ответ на свой вопрос или сомневаетесь в немравильВы можете воспользоваться приведенной ниже формой, чтобы улучшить свой ответ. Или воспользуйтесь формой поиска, чтобы найти похожие ответы по предмету Геометрия.
В треугольнике ABC — вершины A, B и C треугольника стороны отрезков AB, BC и CA. треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB углы треугольника. Часто углы треугольника обозначаются одной буквой: ∠A, ∠B, ∠C .
Количество биссектрис в треугольнике
Но вернемся к нашей главной теме. И давайте ответим на этот вопрос. – сколько БИССЕКТРИС есть в треугольнике?
Ответ в принципе логичен и следует из названии нашей геометрической схемы. Треугольник три угла. А соответственно, и биссектрис также будет иметь три — по одной на каждую вершину.
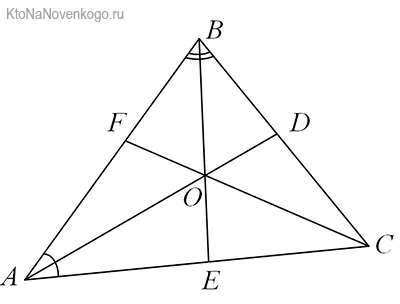
Опять же, давайте посмотрим на рисунки. В этом случае мы можем ясно видеть, что у треугольника АВС (именно так Геометрия определяет эту фигуру — по имени ее вершин) три БИССЕКТРА. Это отрезки AD, BE и CF.
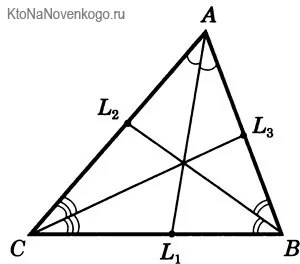
На чертежах BISSECTRISE назван следующим образом. образом. Вы видите странные изогнутые линии между отрезками AC/AL1 и AB/AL1? Именно так они и маркируются. углы. И тот факт, что они оба отмечены одинаковыми штрихами, говорит о том, что углы равны. А значит, отрезок AL1 — это БИССЕКТРИСА.
То же самое относится и к к углам между AB/DL2 и BC/BL2. Они отмечены одинаковыми двойными тире. Следовательно, отрезок BL2 – биссектриса. А углы AC/CL3 и BC/CL3 отмечены тройным дефисом. Это показывает, что отрезок CL3 также является биссектрисой.
Пересечение биссектрис треугольника
Как вы можете видеть по приведенным выше рисункам, у биссектрис треугольника есть одна важная особенность. В частности:
Биссектрисы треугольника они всегда пересекаются в одной и той же точке., называемой инцентром!
Это правило является аксиомой (аксиома это такое?) и не допускает никаких исключения. Другими словами, здесь такого быть не может :
Если вы видите такую картину, то вы, конечно, не видите перед собой БИССЕКТРИСУ. В любом случае, минимум один отрезок таковоЭто не так. А может, и все три.
И есть еще один интересный факт, связанный с пересечением биссектрис треугольника.
Центр пересечения биссектрис в треугольнике является центром окружности, который списан в эту фигуру.
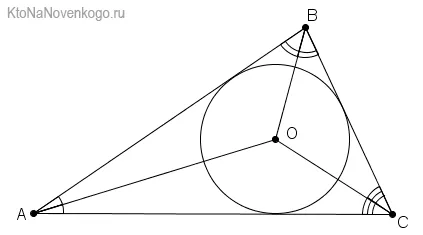
Это свойство биссектрис это интересно выглядит не только на рисунках. Это часто помогает решить сложные задач.
Свойство основания биссектрисы
Каждый BISSECTRISE имеет основание. Так называют точку пересечения со стороной треугольника. Например, В нашем случае это будет точка «К».
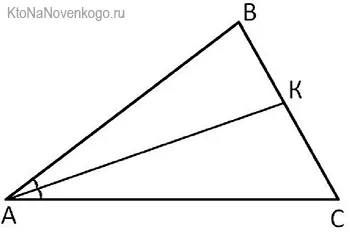
И с этим основанием связана Очень интересный момент. теорема. Она гласит, что
Биссектриса треугольника делит противоПоэтому в данном случае базовой точкой является точка K. два отрезка. И их отношение равно отношению двух прилежащих сторон .
Звучит несколько Это немного сложно, но на самом деле выглядит довольно просто. Отношения отрезков на основании биссектрисы — является BK/CC. И отношения влежащих стороны равны AB/AC. И оказалось, что в нашем случае. теорема выглядит вот так:
Интересно, что для этого теоремы будет справедли другое заявление:
Ну, как В математике часто бывает так, что pравило работает и в обратном направленyi. То есть, если вы знаете длины всех сторон и их соотношения равны, то можно сделать прийти к выводу, что мы имеем дело с МИСКУССИЕЙ, и, следовательно, будет легче определить величину угла треугольника.
Биссектриса треугольника – отрезок, который выходит из верхней части фигуры, а другой конец крепится сбоку, которая расположена напротив Другой конец крепится к боковой части фигуры.остранстДругой конец фигуры помещается на другую сторону фигуры.
Треугольник
Треугольник — это замкнутая пунктирная линия, состоящая из трех звеньев:
Вершины ломаной называются вершинами треугольника, и его соединения являются сторонами треугольника. Углы, образованные двумя сторонами треугольника треугольника, называются углами треугольника:
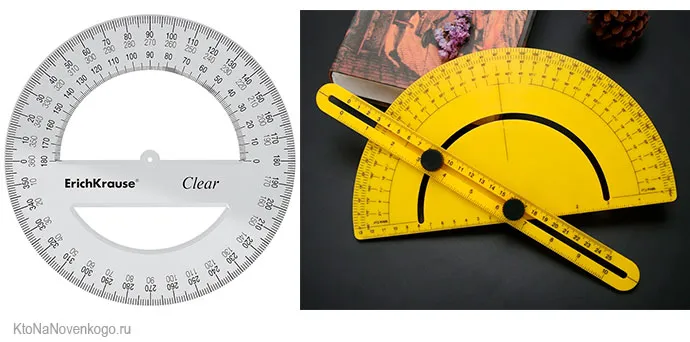
В треугольнике ABC — вершины A, B и C треугольника стороны отрезков AB, BC и CA. треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB углы треугольника. Часто углы треугольника обозначаются одной буквой: ∠A, ∠B, ∠C .
Треугольник обычно обозначается тремя буквами в его вершинах. На сайтепример, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется. Таким образом, написание ABC будет выглядеть следующим образом:треугольник ABC .
У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — перпендикуляр, проведенный из вершины треугольника к его основанию. Высота треугольника может упасть на продолжение базы.
Отрезок BN — это высота ABC: Раздел EL высота DEF, падает на продолжение стороны DF .
Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Биссектриса треугольника – отрезок, который выходит из верхней части фигуры, а другой конец крепится сбоку, которая расположена напротив Другой конец крепится к боковой части фигуры.остранстДругой конец фигуры помещается на другую сторону фигуры.
Свойства
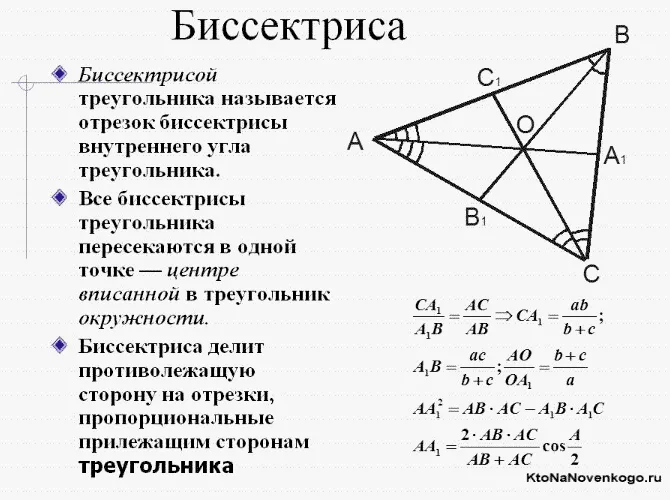
Кроме определения, Вы можете найти в учебнике не так многие свойства этой геометрической понятия. Первое свойство биссектрисы треугольника, с которым знакомят школьников, – центр вписанной окружности, а второе, напрямую связанное с ним, — пропорциональность отрезков. Суть заключается в следующем:
- Какая бы ни была делящая прямая, есть пункты, содержащиеся в нем, которые имеют одинаковое расстояние до сторон, которые составляют пространство между лучами.
- Для того чтобы вписать в треугольную фигуру окружность, необходимо определить точку, в которой будут пересекаться эти отрезки. Это и есть центральная точка окружности.
- Части стороны треугольной геометрическая форма, на которые разделить на прямая, находятся в пропорциональной зависимости. от образующих угол сторон.
Постараемся привести в системе другие характеристики и представляют дополнительные факты, которые поможет глубже изучить преимущества этой геометрической формы понятия.
Это интересно! Расчет радиуса: как найти длину окружности зная диаметр
Длина
Одним из видов задач, которые Задача студентов состоит в том, чтобы найти длину биссектрисы угла треугольника. Первый вариант, в котором длина, содержит такие данные:
- величина пространстУгол между лучами, начиная с вершины которого выходит данный отрезок,
- длины сторон, которые образуют этот угол.

Для решения данной задачи используйте формулу, со значением которой заключается в нахождении соотношения между 2-кратным произведением величин сторон, образующих угол, и косинусом его половины к сумме сторон.
Рассмотрим на определенном примере. Предположим, что дана фигура ABC, в которой отрезок проведен из угла A и пересекает сторону BC в точке K. Пусть Y — значение A. Пусть это дает AK = (2*AB*AC*cos(Y/2))/(AB+AC).
Это интересно! Первый признак равенства треугольников: доказательство
Второй вариант задачи, в котором определяется длина биссектрисы треугольника, содержит такие данные:
При решении задачи такого типа первоначально определяем полуокружность. Для этого складываем значения всех сторон и делим пополам: p = (AB+B+CU)/2. Тогда применяеm — формула расчета, с помощью которой определялась длина данного отрезка в предыдущей задаче. Все, что нам нужно, это некоторые Изменение формулы в соответствии с новыми параметрами. Итак, заключается в нахождении отношения двойного корня второй одной степени от произведения длин сторон, которые в вершине на радиус и на разность между радиусом и длиной противолежащей ему стороны к сумме сторон угла. То есть, AK=(2٦AB*AC*p*(p-BC))/(AB+AC).
Вниманee. Чтобы легче было усвоить материал, можно обратиться к забавным историям в интернете о приключениях этого прямой.
Частные случаи
Биссектриса прямоугольного треугольника Он обладает всеми обычными свойствами. Однако есть особый случай, который следует отметить, который присущ только ей: при пересечении отрезков, основания которых являются вершинами острых углов прямоугольного треугольника, угол между лучами равен 45 градусам.
Биссектриса равнобедренного треугольника также имеет свои особенности:
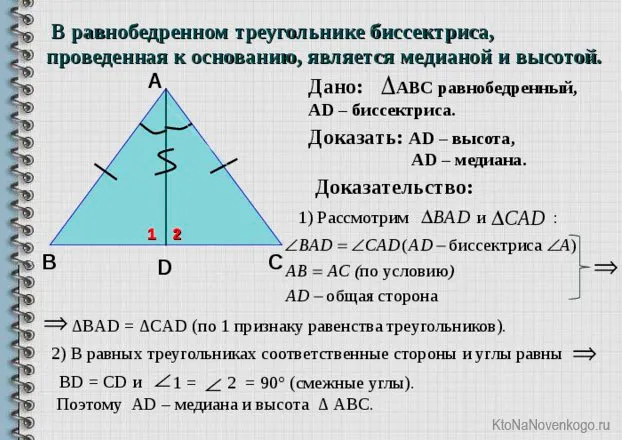
- Если основание этого отрезка – вершина, противолежащая в основании, то это и высотой, и медианой.
- Если отрезки проведены из вершин углов в основании, то его длины равны между собой.
Это интересно! Чему равна и как найти площадь равностороннего треугольника








