Для того, чтобы перпендикулярность пересекающихся плоскостей является явным, необходимо и достаточно, чтобы нормальные векторы конкретных плоскостей пересекаются под прямым углом.
Когда плоскость перпендикулярна плоскости
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Рассмотрим две плоскости α1 и один2заданные в каждом случае уравнениями:
Из угла между двумя плоскостями возьмем один из образованных ими плоских углов плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α1 и один2 равен одному из заданных смежных двугранных углов или. Поскольку, и, то, следовательно, .
Пример. Определите угол между плоскостями x +2 y -3 z +4=0 и 2 x +3 y + z +8=0.
Условие параллельности двух плоскостей.
Две плоскости α1 и один2 параллельны только в том случае, если, когда их нормальные векторы параллельны друг другу, т.е. .
Итак, две плоскости параллельны только в том случае, когда коэффициенты в соответствующих координатах пропорциональны
Условие перпендикулярности плоскостей.
Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, и так далее, или .
-
Напишите уравнение плоскости, через точку
M (-2; 1; 4) параллельно плоскости 3x +2 y -7 z +8=0.
Уравнение плоскости находится в виде Ax+By+Cz+D = 0. Из условия параллельности плоскостей Из этого следует, что: Поэтому мы можем установить A =3, B =2, C =-7. Поэтому уравнение плоскости имеет вид3x+2y-7z+D=0.
Так как M Î a, то 6+2-28+D=0, D=32.
Таким образом, искомое уравнение равно 3 x +2 y -7 z +32=0.
Поскольку M1 Î α, используя уравнение. плоскости, которая проходит через данную точку, следует, что A ( x -1)+ B ( y -1)+ C ( z -1)=0.
Затем, предполагая, что M2 Î α, то -A -2 C =0 или A +2 C =0.
Учтем, что заданная плоскость перпендикулярна это желаемое. Следовательно, A+B+C =0.
Мы выражаем коэффициенты A и B через C: A =-2 C, B =C и подставьте их в исходное уравнение: -2 C ( x -1 ) + C ( y -1 ) + C ( z -1 ) =0.
Окончательный результат -2 x + y + z =0.
Поскольку M является Î α, A ( x +2 ) + B ( x -3 ) + C ( z -6 ) = 0.
По условию задачи, поэтому
Итак уравнение плоскости имеет вид 13( x +2)-8( y -3)+ z -6=0 или 13 x -8 y + z+ 44=0.
ЛИНИЯ В ПРОСТРАНСТВЕ.
ВЕКТОРНОЕ УРАВНЕНИЕ ЛИНИИ.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ЛИНИИ
Положение линии в пространстве полностью определяется определением неподвижной точки M 1 и вектор, параллельный этой прямой.
Вектор, который параллелен прямой, называется ведущим вектором этой прямой.
Таким образом, прямая l должна проходить через точку M 1( x 1, y 1, z 1), которая лежит на прямой и параллельна вектору.
Рассмотрим любую точку M(x, y, z) на прямой. Из рисунка видно, что .
Векторы и и коллинеарны так, что существует число t такое, что коэффициент t может принимать любое числовое значение, зависящее от положения M на прямой. Множитель t называется параметром. Обозначив радиус-векторы M 1 и M соответственно, получаем. Это уравнение называется векторным уравнением прямой линии. Это показывает, что каждому значению параметра t соответствует радиус-вектор точки M, лежащей на прямой.
Положение линии в пространстве полностью определяется определением неподвижной точки M 1 и вектор, параллельный этой прямой.
Перпендикулярные плоскости, условие перпендикулярности плоскостей
Данный документ посвящен следующим темам перпендикулярным плоскостям. В ней будут даны определения, обозначения и примеры. В нем будет сформулирована характеристика перпендикулярности плоскостей и условие, что делает его осуществимым. Решения таких проблем будут рассмотрены на примерах.
Если между пересекающимися линиями есть угол, то можно говорить об определении перпендикулярных плоскостей.
При условии, что угол между перпендикулярными линии равны 90 градусам, они называются перпендикулярными.
Обозначение перпендикулярности обычно записывается с символом » ⊥ «. Если в условии дано, что плоскости α и β перпендикулярные, тогда обозначение принимает вид a ⊥ b. На следующем рисунке это показано подробно.
Когда в улови дано, что плоскость Если a и b перпендикулярны друг другу, это означает, что a перпендикулярно b и наоборот. Это плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимными перпендикулярными потому что они образуют прямой угол в точке пересечения.
Перпендикулярность плоскостей — Знак и понятие перпендикулярности
На практике вы можете столкнуться с проблемами, когда необходимо определить следующее. перпендикулярность заданных плоскостей. Сначала нужно определить угол между ними. Если она составляет 90 градусов, то считается, что перпендикулярными из определения.
Для доказательства перпендикулярности двух плоскостей для применения характеристики. перпендикулярности двух плоскостей. Формулировка включает в себя термины перпендикулярная прямая и плоскость. Давайте напишем точное определение атрибута перпендикулярности как теорема.
Если один из двух приведенных плоскостей пересекает линию, перпендикулярную другой линии плоскости, тогда данный плоскости перпендикулярны.
Доказательство теоремы можно найти в учебнике геометрии для 10-11 классов, где оно подробно описано. Из доказательства следует, что если плоскость перпендикулярна это пересечение двух данных плоскостей, тогда он перпендикулярен к каждому из них плоскостей.
Существует необходимая и достаточная условия для доказательства. Рассмотрим для перпендикулярности двух заданных плоскостей, как доказательство их перпендикулярности, в прямоугольной системе координат трехмерного пространства. Чтобы доказательство было верным, необходимо применить определение нормального вектора плоскости, что необходимо и достаточно для доказательства того, что условие перпендикулярности плоскостей.
Для того, чтобы перпендикулярность пересекающихся плоскостей является явным, необходимо и достаточно, чтобы нормальные векторы конкретных плоскостей пересекаются под прямым углом.
Мы рассматриваем прямоугольную систему координат в трехмерном пространстве. Если мы имеем n 1 → = ( A 1, B 1, C 1 ) и n 2 → = ( A 2, B 2, C 2 ), которые являются нормальными векторами данного плоскостей a и b, то необходимо и достаточно условием перпендикулярности векторов n 1 → и n 2 → имеет вид
n 1 →, n 2 → = 0 ⇔ A 1 — A 2 + B 1 — B 2 + C 1 — C 2 = 0.
Из этого следует, что n 1 → = ( A 1, B 1, C 1 ) и n 2 → = ( A 2, B 2, C 2 ) являются нормальными векторами данных. плоскостей, и для реальности перпендикулярности a и b необходимо и достаточно, чтобы скалярное произведение векторов n 1 → и n 2 → было равно нулю и имело вид n 1 →, n 2 → = 0 ⇔ A 1 — A 2 + B 1 — B 2 + C 1 — C 2 = 0.
Давайте рассмотрим примеры более подробно.
Определить перпендикулярность плоскостей, В прямоугольной системе координат O x y z трехмерного пространства, заданной уравнениями x — 3 y — 4 = 0 и x 2 3 + y — 2 + z 4 5 = 1 ?
Чтобы найти ответ на вопрос о перпендикулярности сначала определите координаты нормальных векторов, заданных словами плоскостей, и тогда можно проверить на перпендикулярность.
x — 3 y — 4 = 0 является общим уравнением плоскости, Отсюда сразу же можно преобразовать координаты нормального вектора, равного n 1 → = ( 1, — 3, 0 ).
Чтобы определить координату нормального вектора плоскости x 2 3 + y — 2 + z 4 5 = 1 преобразуем из уравнения плоскости в отрезках к общему.
x 2 3 + y — 2 + y — 2 + z 4 5 ⇔ 3 2 x — 1 2 y + 5 4 z — 1 = 0.
Тогда n 2 → = 3 2, — 1 2, 5 4 — координаты нормального вектора плоскости x 2 3 3 + y — 2 + z 4 5 = 1 .
Теперь вычислим скалярное произведение векторов n 1 → = ( 1, — 3, 0 ) и n 2 → = 3 2, — 1 2, 5 4 .
Мы предполагаем, что n 1 →, n 2 → = 1 — 3 2 + ( — 3 ) — 1 2 + 0 — 5 4 = 3 .
Мы видим, что он не равен нулю, следовательно, эти векторы. не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.
Положение линии в пространстве полностью определяется определением неподвижной точки M 1 и вектор, параллельный этой прямой.
Перпендикулярность плоскостей
Две плоскости называются перпендикулярными если двугранный угол между ними равен 90°.
- Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, проведите линию, перпендикулярную другой плоскости, тогда эта перпендикулярная линия полностью лежит на первой. плоскости.
- Если в одной из двух перпендикулярных плоскостей перпендикуляра к линии пересечения, то этот перпендикуляр перпендикулярен второму плоскости.
- Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения
- Если третья плоскость, перпендикулярная пересечение этих двух плоскостей, пересекает их по перпендикулярным прямым.
теорема. ПЕРПЕНДИКУЛЯР ПЛОСКОСТЕЙ.
Если плоскость через линию перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Доказательство:
Пусть — плоскость b — линия, перпендикулярная ей, -. плоскость через линию b, а c — линия, проходящая через точку
перекресток плоскости и .
Докажем, что плоскости и перпендикулярно к нему. Позвольте нам набрать плоскости через точку пересечения линии b с плоскостью прямую а, перпендикулярную прямой с .
Проведите линии a и b плоскость. Она перпендикулярна через линию c, так как линии a и b являются перпендикулярны, то плоскости и перпендикулярны.
\(ABCD\) — это тетраэдр (треугольная пирамида). \(\(\угольник BAB=\угольник DAC=\угольник ACB=90^\circ, AC=CB=5, DB=5\sqrt5\). Найдите двугранный угол \(ABCD.\)
Научная электронная библиотека

Если плоскость которая перпендикулярна другой плоскости, тогда данный плоскость перпендикулярна другой плоскости.
Если две плоскости взаимно перпендикулярны, затем линия на плоскости перпендикулярно линии пересечения плоскостей, перпендикулярно другойплоскости.
На рисунке 4.4 показаны два проектора. 4.4 показывает два прогноза плоскости b, c и произвольные плоскость d, следы которой проходят через следы линии a.
На рис. 4.5 показан составной чертеж с двумя взаимнымиперпендикулярные плоскости.
Это плоскость, определяемый треугольником ∆ABC и плоскость, определяемая пересекающимися линиями KM и KN. Их перпендикулярность подтверждает прямая b, перпендикулярная плоскости Δ ABC, поскольку проекции перпендикулярны соответствуют проекциям линий плоскости D ABC. Проекции линий плоскости D ABC плоскости Δ ABC удовлетворяют условиям перпендикулярности прямой b и плоскости, потому что b1 ⊥ h1 и b2 ⊥ f2.
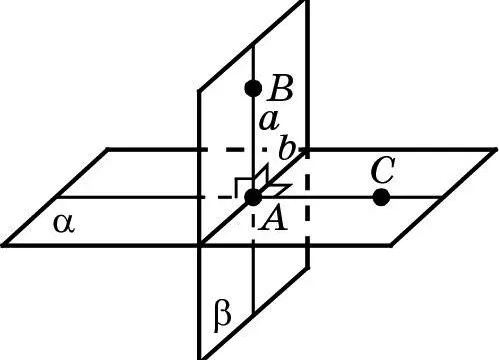
Рис. 4.4. Условие перпендикулярности плоскостей
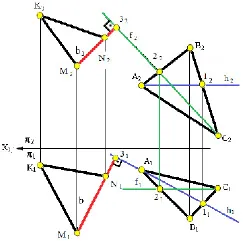
Рисунок 4.5: Изображение двух взаимныхперпендикулярных плоскостей
По условию перпендикулярности, любая плоскость (например, плоскость, заданная двумя пересекающимися прямыми KM и KN) по прямой. b, перпендикулярную плоскости D ABC перпендикулярнаплоскости Δ АВС.








