Если числитель и знаменатель равны, то дробь не появляется. В результате получается число: 1. Также, если числитель умножить на знаменатель, то дробь сразу же прослеживается до целого числа.
Десятичные дроби
Мы уже упоминали, что дроби могут быть как дробными, так и десятичными. До сих пор мы изучали несколько вопросов о дробях. Мы узнали, что дроби могут быть обычными и неправильными. Мы также узнали, что дроби можно уменьшать, прибавлять, отнимать, умножать и делить. Мы также узнали, что существуют смешанные числа, состоящие из целых и дробных частей.
Мы не до конца изучили фракции. Есть много более светлых оттенков и деталей, о которых нам нужно поговорить, но сегодня мы начинаем изучать дробные дроби, потому что нам нужно объединить целые десятичные и дробные дроби. Другими словами, если у вас есть проблема, вам нужно использовать оба типа дробей.
Этот урок может показаться сложным и запутанным. Это совершенно нормально. Этот тип урока необходимо исследовать, а не просто обойти.
Выражение величин в дробном виде
Иногда полезно показать что-то в долях. Например, одна десятая часть десятичного измерения описывается как
Это представление означает, что 15 метров разделены на 10 равных частей и части этих 10 частей. В этом случае одна часть от десяти равна одному сантиметру.
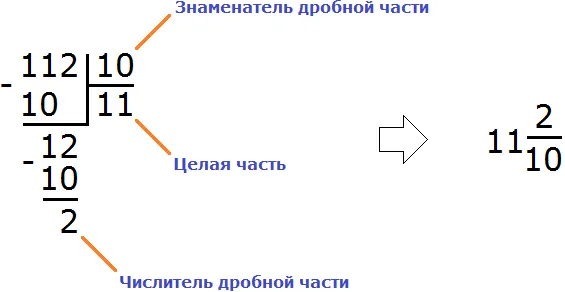
Рассмотрим следующий пример. Предположим, что только 6 см и еще 3 мм нужно выразить в виде дробей.
Таким образом, уже есть 6 см.
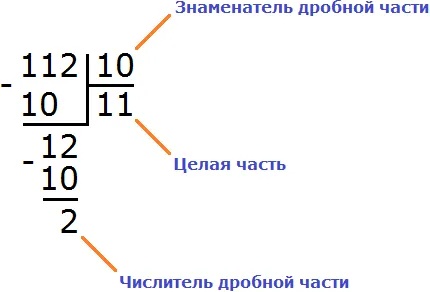
Однако остается еще 3 мм. Как бы вы отобразили эти 3 мм, но в сантиметрах? Дробные дроби будут как бы спасать ситуацию. Один сантиметр равен 10 миллиметрам. Три миллиметра — это три части от десяти. Все три части десяти записываются как CM.
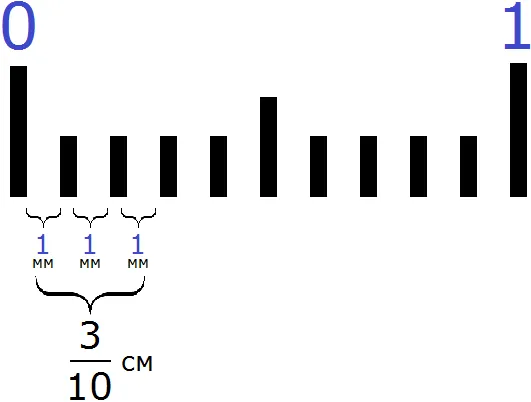
Формула CM означает, что один сантиметр делится на десять равных частей и из этих десяти частей берутся три части.
Следовательно, существует шесть сантиметров и три десятых сантиметра.
Число 6 показывает количество целых чисел и дробей дробей. Эта дробь обозначается «шесть целых и три десятых».
Дроби 10, 100 или 1000 могут быть записаны без знаменателя. Запишите сначала целое число, затем числитель дробной части. Целое число отделяется от дробной части запятой.
Например, напишите без знаменателя. Сначала напишите целое число. Целое число равно 6.
Целое число записано. Сразу после написания неотъемлемой части, партии.
А теперь запишите числитель дробной части. В смешанных числах числитель дробной части равен 3. Напишите 3 после вечеринки.
Все числа, представленные в такой форме, называются дробными десятичными дробями.
Поэтому вы можете использовать диаграмму десятичных точек для отображения сантиметров 6 см и далее 3 мм.
Внешний вид:.
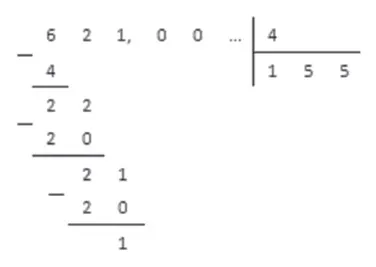
На практике десятичные дроби ничем не отличаются от обычных дробей и смешанных чисел. Особенность этих дробей в том, что в знаменателе их дробной части стоят числа 10, 100, 1000 или 10000.
Как и смешанные числа, дробные дроби имеют как целую, так и дробную часть. Например, в смешанном числе целое число равно 6, а дробная часть равна 6.
В десятичной дроби 6,3 целое число равно 6, а дробная часть является числителем дроби, то есть числом 3.
Дробь также образуется без целых чисел и с числовыми значениями 10, 100 и 1000 в знаменателе. Например, дробь дается без целого числа. Чтобы записать такую дробь в виде десятичной дроби, напишите сначала 0, затем партицию, а затем числовую часть дроби. Дроби без знаменателей записываются следующим образом.
‘Нулевое целое число, пять знаков после запятой’, которое гласит.
Перевод смешанных чисел в десятичные дроби
Запишите смешанные числа без знаменателей, переведите их в десятичную дробь. Есть несколько вещей, которые вам нужно знать о превращении дробей в десятичные дроби.
При записи целых дробей важно измерить количество нулей в знаменателе дроби, поскольку количество нулей в дроби должно быть равно количеству цифр после запятой в дроби. Что это значит, рассмотрим на следующем примере. Превратите смешанное число в десятичную дробь.
Сначала напишите всю часть и откройте партию.
Тогда можно сразу написать числитель дробной части и десятичная дробь готова, но нужно подсчитать количество нулей, содержащихся в знаменателе дробной части.
Поэтому измерьте количество нулей в дробной части смешанного числа. Вы увидите, что в знаменателе дробной части есть нули. В десятичной дроби после запятой стоит число, которое является числителем дробной части смешанного числа, т.е. числа 2.
Таким образом, смешанное число при переводе в десятичную дробь преобразуется в 3,2. Это десятичное число читается следующим образом
Десятичная», потому что дробная часть смешанного числа содержит число 10.
Пример 2.Преобразование смешанного числа в десятичную дробь.
Напишите целую часть и добавьте партию.
Вы также можете написать дробную часть числа и получить десятичную дробь 5,3, но правила гласят, что после партии знаменатель дробной части смешанного числа должен иметь столько же цифр, сколько и ноль. Затем мы видим, что в знаменателе дробной части есть два нуля. Поэтому дробная часть десятичной дроби должна иметь две цифры после запятой.
В этом случае необходимо изменить числитель дробной части, добавив ноль перед числителем, т.е. перед числом 3
Теперь вы можете перейти к завершению упражнения. Запишите дробную часть после десятичной точки:.
Мы видим, что количество цифр после запятой в знаменателе дробной части смешанного числа равно количеству нулей.
Десятичное число 5.03 читается следующим образом.
«сотни», потому что знаменатель дробной части смешанного числа содержит число 100.
Пример 3. Изменение смешанного числа в дробную десятичную дробь.
Из предыдущего примера мы узнали, что для успешного преобразования смешанного числа в дробь необходимо, чтобы количество цифр в дробной части было равно количеству нулей в знаменателе дробной части.
Прежде чем смешанное число будет преобразовано в дробь, его дробная часть должна быть немного изменена. Это означает, что количество цифр в дробной части числителя и количество нулей в дробной части знаменателя одинаковы.
Во-первых, рассмотрим количество нулей в знаменателе дробной части. Мы видим, что здесь три нуля.
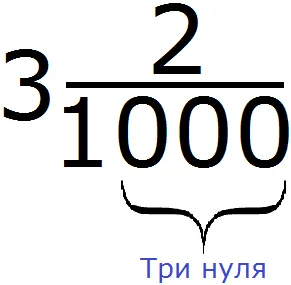
Наша цель — остановиться на трех цифрах в знаменателе дробной части. У нас уже есть цифра, цифра 2. Теперь нам нужно добавить еще две цифры. Это два нуля. Добавьте их перед номером 2. В результате количество нулей в знаменателе совпадает с количеством цифр в числителе.
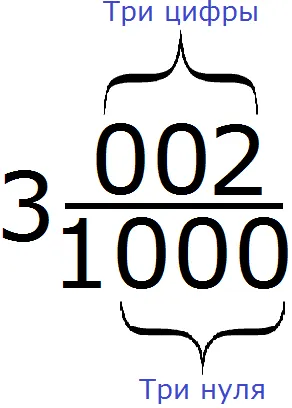
Теперь вы можете преобразовать это смешанное число в дробь. Напишите целые числа сначала и партию:.
Удаление производится так же, как и удаление натуральных чисел в столбцах, при этом сторона ответа явно располагается в той же позиции, что и число, с которым мы работаем.
Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры
Рекомендуется переводить обычные пропорции в десятичные дроби и наоборот, используя удобный расчет. О том, как это сделать, рассказывается в этой статье. Мы рассмотрим правила преобразования дробей в десятичные дроби и наоборот и приведем примеры.
Рассмотрите преобразование дробей в десятичные числа в соответствии с определенным порядком. Сначала мы обсудим, как переводить обычные дроби со знаменателями 10, 100 и 1000. На самом деле, дроби с такими знаменателями сложнее описать как десятичные числа.
Далее мы рассмотрим, как переводить дроби, общие для десятичных чисел, в знаменатели, а также кратные 10. Обратите внимание, что при переводе обычных дробей в десятичные числа вы получаете не только конечные десятичные числа, но и неопытные обычные дробные числа.
Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дроби
Прежде всего, скажем, что перед преобразованием дробей в десятичные числа требуется некоторая подготовка. Что это такое? Количество цифр в числителе равно количеству нулей в знаменателе, потому что нули нужно добавить перед числителем. Например, добавьте нули в числитель слева от 3100 и 3. Согласно приведенному выше правилу, к дроби 610 не требуется прибавлять.
Давайте рассмотрим другой пример. Далее, давайте создадим правило, которое чаще всего используется на более позднем этапе, когда ни у кого нет опыта фрагментации. Например, 1610000 становится 001510000 после добавления нулей в числитель.
Как преобразовать нормальные пропорции, такие как 10, 100 или 1000 знаменателей? с дробными дробями?
Правила преобразования обычных правильных дробей в десятичные дробные числа
- Записываем 0 и ставим после него запятую.
- Записываем число из числителя, которое получилось после дописывания нулей.
Теперь перейдем к примерам.
Пример 1.Преобразование обычных дробей в десятичные дроби
39 Преобразуйте обычную дробь 100 в десятичную дробь.
При рассмотрении дробей сначала не требуется никаких подготовительных действий — количество цифр в числителе будет соответствовать количеству нулей в знаменателе.
Следуя правилам, напишите 0, затем поставьте десятичную дробь и напишите число из числителя. Вы получаете десятичные 0 и 39.
Давайте рассмотрим еще один пример решения на ту же тему.
Пример 2. Преобразование обычных дробей в десятичные дроби
105 10000000 записывается как десятичная точка.
В знаменателе семь нулей, а в числителе только три цифры. Добавьте четыре нуля к числителю перед числом.
Затем напишите 0, затем установите десятичную дробь и напишите число из числителя. Вы получаете десятичный 0, 0000105.
Дроби, рассмотренные во всех примерах, обычно являются правильными дробями. Но как заменить неправильные дроби на десятичные? Сразу скажем, что для таких дробей нет необходимости готовить нули. Давайте сформулируем правило.
Правила преобразования обычных неправильных дробей в десятичные дроби.
- Записываем число, которое находится в числителе.
- Десятичной запятой отделяем столько цифр справа, сколько нулей есть в знаменателе исходной обыкновенной дроби.
Это пример использования правила.
Перевод десятичных дробей в обыкновенные дроби
Теперь пришло время рассмотреть обратный процесс преобразования десятичной дроби в обычный процент. Сформулируйте правило преобразования, состоящее из трех шагов. Как преобразовать десятичные дроби в дробные?
Правила преобразования десятичных дробей в дробные.
- В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
- В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
- При необходимости сокращаем полученную обыкновенную дробь.
Рассмотрим применение этого правила на примере.
Пример 8.Преобразование дробных дробей в десятичные дроби
Преобразуйте 3,025 в дробь.
- В числитель записываем саму десятичную дробь, отбросив запятую: 3025 .
- В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 3025 1000 .
- Полученную дробь 3025 1000 можно сократить на 25, в результате чего мы получим: 3025 1000 = 121 40 .
Переведите десятичные дроби 0 и 0017 из десятичной системы счисления в обычную.
- В числителе запишем дробь 0, 0017, отбросив запятую и нули слева. Получится 17 .
- В знаменатель записываем единицу, а после нее пишем четыре нуля: 17 10000. Данная дробь несократима.
Если в дробной дроби есть целое число, то дробь можно сразу преобразовать в смешанное число. Как это может произойти?
Давайте сформулируем другое правило.
Правило преобразования десятичной дроби в смешанное число.
- Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
- В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
- В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.
Пример 10.Преобразование дробных дробей в смешанные числа
Пусть 155 и 06005 представлены в виде смешанных чисел.
- Записываем число 155, как целую часть.
- В числителе записываем цифры после запятой, отбросив нуль.
- В знаменателе записываем единицу и пять нулей
Возьмите смешанное число: 155,6005,100000.
Дробная часть может быть уменьшена на 5. Уменьшите его и получите конечный результат.
155, 06005 = 155 1201 20000
Перевод бесконечных периодических десятичных дробей в обыкновенные дроби
Рассмотрим пример дроби, преобразованной в повторяющуюся десятичную дробь. Прежде чем начать, давайте заявим, что каждая дробь может быть преобразована в обычную дробь.
В простейшем случае период дроби равен нулю. Дробь с нулевым периодом заменяется десятью десятичными знаками, и процесс преобразования таких дробей возвращается к преобразованию конечных дробей.
Пример 11.Преобразование дробных дробей в обычные дробные дроби
Преобразуйте периодическую дробь 3, 75 (0).
Используя нули справа, вы получите конечную десятичную дробь 3, 75.
Следуя алгоритму, описанному в предыдущем пункте, преобразуя эту дробь в обычную дробь, получаем
3, 75 (0) = 3, 75 = 375 100 = 15 4.
Что произойдет, если дробный период будет ненулевым? Периодические фракции следует рассматривать как сумму условий для сокращения геометрической прогрессии. Давайте проиллюстрируем это на примере.
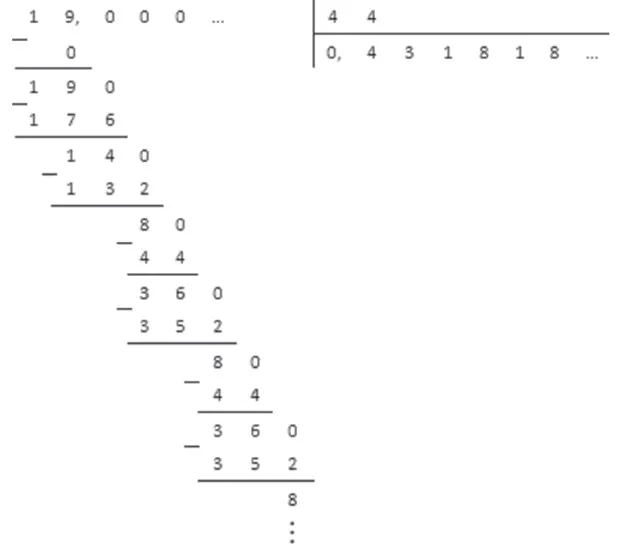
В некоторых случаях может потребоваться деление на угол или использование калькулятора для нахождения коэффициента. Также невозможно возвести некоторые дроби в конечную десятичную дробь. Например, деление не даст конечного результата для части 1/3.
Определение периодической дроби
Периодические дроби — это бесконечные десятичные дроби, в которых определенная группа чисел повторяется периодически, начиная с определенного момента времени.
Периодическая часть дроби — это набор повторяющихся цифр, составляющих значащую часть.
В сокращенном обозначении периодических дробей повторяющиеся цифры записываются в скобках и называются периодом дроби. Например, вместо 1,555 напишите 1, (5), что означает «одна целая и пять точек».
Значительная часть остатка, которая не повторяется, называется ациклической дробью.
Виды периодических дробей: чистые и смешанные.
Чисто десятичные журналы — это десятичные цифры с точкой сразу после десятичной цифры. Примеры: 1, (4); 4, (25); 21, (693).
Десятичные журналы — это десятичные цифры с партией, за которой следует запись с периодом из одной или нескольких цифр. Например, 3,5 (1) — 0,02 (89) — 7,0 (123).
Давайте рассмотрим несколько примеров дробей, чтобы научиться распознавать части и периоды.
Без журнала: 0 — Журнальная часть: 3 — Продолжительность периода: 1.
Читать следующим образом: ноль три стороны периода.
Без журнала: 0.58 — Части журнала: 3 — Продолжительность: 1 раз.
Читайте так: нулевая партия 58 см и три точки.
Без журнала: 1, Части журнала: 54, Продолжительность: 2.
Читать следующим образом: одна точка на 54 см.
25/39 = 0.641025 641025. = 0, (641025)
Без журнала: 0 — Журнальные части: 641025 — Продолжительность периода: 6.
Читайте следующим образом:Нулевая партия Шесть1400 — Периоды от 1 до 22 миллионов.
54 см за период.
Без журнала: 3066 — Части журнала: 6 — Продолжительность периода: 1.
Читать далее: 360 партий и шесть партий.
Перевод периодической дроби в обыкновенную
Узнайте, как преобразовать дробные дроби в обычные.
Если дробный период равен нулю, то решение быстрое. Периодические дроби с нулевым периодом заменяются конечными дробными числами, а процесс обращения таких пропорций возвращается к инверсии конечных дробей.
Пример. Преобразуйте периодическую дробь 1,32 (0) в обычную дробь.
Оставьте все нули справа и получите конечную десятичную дробь 1,32. Затем следуйте алгоритму предыдущего пункта.
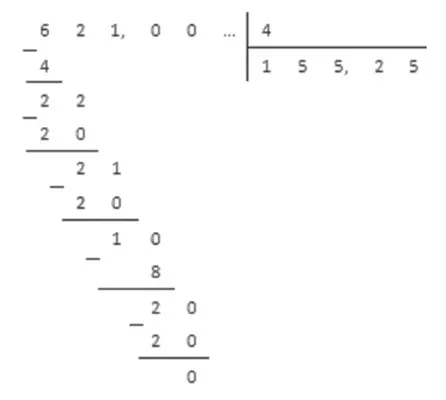
Рассмотрим другой пример с дробными периодами, равными нулю.
Как записать периодическую дробь 10.0219 (37) в виде обычной дроби:.
Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву k.
Во-первых, перед первой значащей цифрой стоит ноль. Отбросьте нули. Символизируйте результат результата.
Теперь остается только заменить все значения типа и получить ответ.

Решена проблема преобразования неопытных периодических дробей в обычные дроби.
Существует еще один способ преобразования периодических дробей в обычные дроби. Сделайте это и рассматривайте дробь периода как сумму условий сокращения геометрической прогрессии. Например, чтобы.
0, (98) = 0.98 + 0.0098 + 0.000098 + 0.00000098 + .
Существуют виды сумм членов бесконечно убывающих геометрических прогрессий. Если первый член прогрессии равен b, а q-знаменатель равен 0< q < 1, то сумма равна b/(1-q) .
Пример. Преобразуйте периодическую дробь 0 (7) в обычную дробь.
С первым членом 0,7 и знаменателем 0,1 найдена бесконечная убывающая геометрическая прогрессия.
0, (7) = 0.7 + 0.07 + 0.007 +. = 0.7/(1-0.1) = 0.7/0.9 = 7/9.
Таким образом, существует два типа периодических дробей. В следующем разделе описаны различные способы их преобразования в обыкновенные дроби.
Перевод смешанной периодической дроби в обыкновенную
Разница между смешанными периодическими дробями в десятичной дроби заключается в том, что они начинаются с одной или нескольких цифр после десятичной точки.
Чтобы записать смешанные периодические дроби в виде простых дробей, удалите число перед первым периодом до второго периода и запишите результат в числителе.
В знаменатель нужно поместить число, содержащее такое же количество девяток, как и число периода, ноль в конце и число, содержащее больше цифр между десятичной дробью и периодом.








