\Согласно ዤ(ዤ треугольник ABC = ዤ треугольник ADC ዤ) свойству 1: ዤ(AB = CD \), ዤ(ዤ угол 1 = ዤ угол 2ዤ)ዤ(AB \) и ዤ(CD \) параллельны и ዤ(AC \) квадратичны.
Параллелограммы
Признак: если четырехугольник прямоугольный, то его противоположные стороны равны.
Доказательство: если противоположные стороны четырехугольника равны, то это прямоугольник.
Доказательство: если четырехугольник имеет две равные и параллельные противоположные стороны, то он является прямоугольником.
СВОЙСТВО: Если четырехугольник является прямоугольником, то его диагонали делятся пополам в точке пересечения.
Доказательство: если у четырехугольника диагональ в точке пересечения делится пополам, то это прямоугольник.
Признак: если четырехугольник является прямоугольником, то сумма углов, касательных к любой стороне, равна 180°.
Доказательство: если сумма углов, касательных к любой стороне четырехугольника, равна 180°, то это прямоугольник.
Свойство: если четырехугольник является прямоугольником, то его противоположные углы равны.
Доказательство: если противоположные углы четырехугольника равны, то четырехугольник является прямоугольником.
Свойство: если четырехугольник является прямоугольником, то каждая диагональ делит его на два равных треугольника.
Доказательство: если каждая диагональ четырехугольника делит его на два равных треугольника, то четырехугольник является прямоугольником.
Признак: если четырехугольник является прямоугольником, то его диагонали делят его на четыре треугольника равной площади (равные треугольники)
Доказательство: четырехугольник является прямоугольником, если его диагонали делят его на четыре треугольника равной площади (равные треугольники).
Свойства и признаки прямоугольника
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Прямоугольник | Прямоугольником называют параллелограмм, у которого все углы прямые | |
| Свойство | Равенство диагоналей |  |
Если параллелограмм является прямоугольником, то его диагонали равны |
| Признак | Если у параллелограмма диагонали равны, то он является прямоугольником |
| Определение: прямоугольник | |
| Прямоугольником называют параллелограмм, у которого все углы прямые | |
| Свойство: равенство диагоналей | |
 |
Если параллелограмм является прямоугольником, то его диагонали равны |
| Признак: равенство диагоналей | |
 |
Если у параллелограмма диагонали равны, то он является прямоугольником |
| Прямоугольник |
Определение: прямоугольник — это прямоугольник, у которого все углы правильные.
Свойство: если прямоугольник является прямоугольником, то его диагонали равны.
Доказательство: если диагонали прямоугольника равны, то это прямоугольник.
Свойства и признаки ромба
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Ромб | Ромбом называют параллелограмм, у которого все стороны равны | |
| Свойство | Биссектрисы углов диагонали | Если параллелограмм является ромбом, то его диагонали является биссектрисами углов | |
| Признак | Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом | ||
| Свойство | Перпендикулярность диагоналей | Если параллелограмм является ромбом, то его диагонали перпендикулярны | |
| Признак | Если у параллелограмма диагонали перпендикулярны, то он является ромбом |
| Определение: ромб | |
| Ромбом называют параллелограмм, у которого все стороны равны | |
| Свойство: биссектрисы углов и диагонали | |
| Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов | |
| Признак: биссектрисы углов и диагонали | |
| Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом | |
| Свойство: перпендикулярность диагоналей | |
| Если параллелограмм является ромбом, то его диагонали перпендикулярны | |
| Признак: перпендикулярность диагоналей | |
| Если у параллелограмма диагонали перпендикулярны, то он является ромбом | |
Определение: ромб — это прямоугольник, у которого все стороны равны.
ДОКАЗАТЕЛЬСТВО: Если диагонали прямоугольника являются биссектрисами его углов, то прямоугольник является ромбом.
Свойство: если прямоугольник является ромбом, то его диагонали перпендикулярны
Доказательство: если диагональ прямоугольника перпендикулярна, то он является ромбом
\Согласно ዤ(ዤ треугольник ABC = ዤ треугольник ADC ዤ) свойству 1: ዤ(AB = CD \), ዤ(ዤ угол 1 = ዤ угол 2ዤ)ዤ(AB \) и ዤ(CD \) параллельны и ዤ(AC \) квадратичны.
Определение параллелограмма
Прямоугольники — это четырехугольники с противоположными сторонами, параллельными и попарно равными. Как выглядит прямоугольник:.
Особые случаи прямоугольников: ромб, прямоугольник и квадрат.
Диагональ — это отрезок, соединяющий противоположные вершины.
Свойства диагоналей прямоугольника:.
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса прямоугольного угла — это отрезок, соединяющий вершину с одной из двух противоположных точек и делящий угол в средней вершине.
Свойства биссектрис прямоугольника:.
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь прямоугольника:.
Периметр прямоугольника равен сумме его длины и ширины 2.
P = 2 × (a + b), где a — ширина, а b — высота.
Для учащихся с 1 по 11 класс есть отличный дополнительный урок математики!
Свойства параллелограмма
Геометрическая фигура — это произвольный набор точек. Каждая фигура обладает своими уникальными свойствами, которые отличают их друг от друга и помогают решить задачу 8 класса по фигурам.
Изучите основные свойства диагоналей и углов прямоугольника, найдите сумму углов прямоугольника и другие характеристики этой фигуры. Вот:.
Теперь докажем теорему, основанную на первых двух свойствах.
Теорема 1: В прямоугольнике противоположный и противолежащий углы равны.
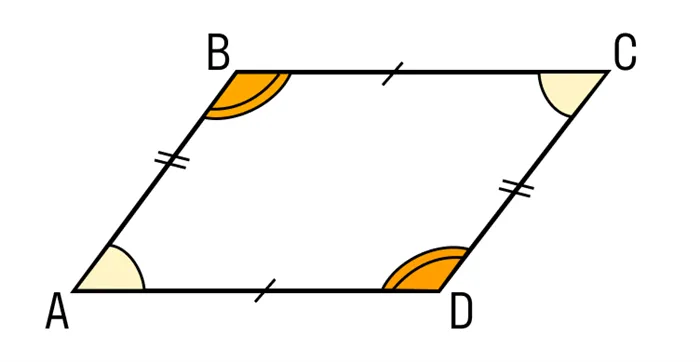
Диагонали пересекаются в каждом выпуклом прямоугольнике. Все, что мы знаем об их пересечении, это то, что оно находится внутри четырехугольника.
Если провести обе диагонали на прямоугольнике, то пересечение делит их пополам. Давайте посмотрим, так ли это на самом деле:.
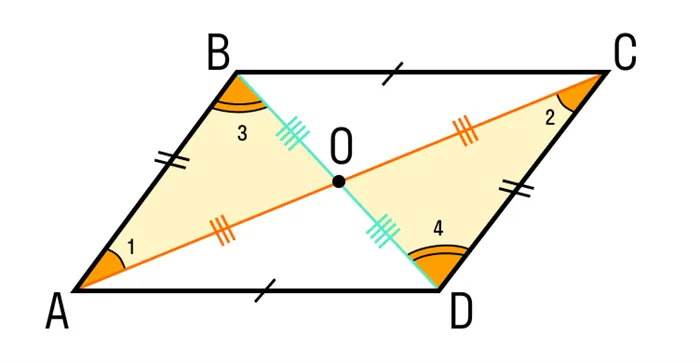
- AB = CD как противоположные стороны параллелограмма.
- ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
- Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO
Теорема доказана. Наша гипотеза верна.
Признаки параллелограмма
Символ прямоугольника помогает нам распознать эту фигуру среди других четырехугольников. Давайте отметим три важных момента.
Первая точка прямоугольника. Если две противоположные стороны четырехугольника одинаково параллельны, то этот четырехугольник является прямоугольником.
Докажите первый признак прямоугольника:.
Шаг 1. Пусть ABCD — четырехугольник.
Чтобы назвать этот четырехугольник, нужно внимательно рассмотреть его стороны.
Теперь вы увидите пару параллельных сторон. Вам нужно доказать, что вторая пара сторон также параллельна.
Шаг 2: Нарисуйте диагонали. Получены два треугольника ABC и CDA. Они равны первой точке равенства, то есть двум сторонам и углу между ними.
Шаг 3. Это также вытекает из того, что треугольники равны.
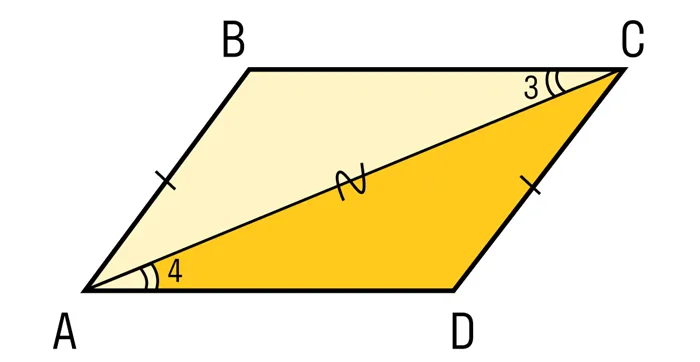
Эти углы также являются углами пересечения прямых CB и AD. А это как раз и есть признак параллельности линий. Таким образом, CB|| AD и ABCD — прямоугольники.
Таким образом, мы доказали наше первое размышление.
Вторая точка прямоугольника. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник является прямоугольником.
Докажем второй признак прямоугольника:.
Шаг 1. Пусть ABCD — четырехугольник.
Шаг 2. Проведите диагональ AC и рассмотрите треугольники ABC и CDA.
Мы видим, что треугольники ABC и CDA равны по третьему признаку, то есть по трем сторонам.
Шаг 3: Найдите уравнения треугольников.
Тогда стороны BC и AD параллельны, так как эти углы являются диагональными при сторонах BC и AD и диагонали AC.
Эти углы являются диагоналями при пересечении AB и CD и при AC. Следовательно, AB и CD также параллельны. Следовательно, ABCD является QTD прямоугольника.
Третья точка прямоугольника. Если разделить диагонали четырехугольника на точки пересечения, то четырехугольник будет прямоугольником.
Докажите, что третья точка прямоугольника:.
Шаг 1.Если диагональ четырехугольника ABCD делится пополам в точке O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними.
Шаг 2. Поскольку треугольники равны, CD = AB.
Эти стороны параллельны CD|| AB, из равенства углов пересечения: ∠1=∠2 (получено из равенства треугольников AOB и COD).
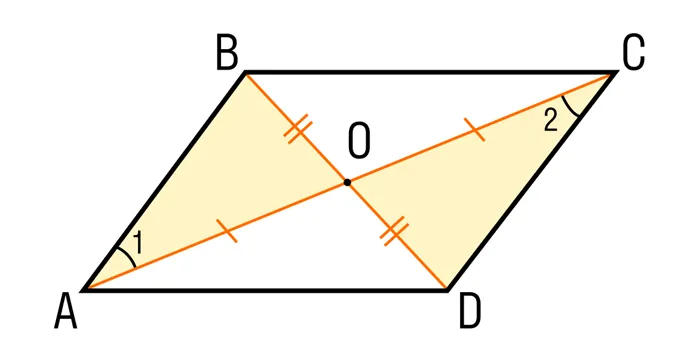
Таким образом, ABCD является прямоугольником по первому доказанному ранее символу. Это нужно было доказать.
Теперь мы знаем свойства прямоугольника и то, что отличает его от других четырехугольников (точки). Если они совпадают, то эти формулы можно использовать для определения прямоугольника. Однако наиболее распространенное определение все же касается параллелизма противоположностей.
3. диагональ делится пополам в точке пересечения. \(⌘ displaystyle AO = OC \) и ⌘(⌘ displaystyle BO = OD \).
Признаки параллелограмма
Четырехугольник ABCD является прямоугольником, если выполняется одно из следующих условий.
1. четырехугольник является прямоугольным, если противоположные стороны четырехугольника попарно равны; 2. четырехугольник является прямоугольным, если диагонали четырехугольника пересекаются и пересечение делит четырехугольник пополам. Четырехугольники одинаково параллельны, и этот четырехугольник является прямоугольником.
Площадь параллелограмма
Где a и b — стороны, AC \ раз BD \ раз \ sin угол AOB «ширина =» «высота =»»/>.
Фонд Викимедиа. 2010.
Полезное
Смотреть что такое «Параллелограмм» в других словарях:
ПРЯМОУГОЛЬНИК — каждый четырехугольник, противоположные стороны которого попарно равны и параллельны — так называется вытянутый четырехугольник с двумя острыми и двумя тупыми углами — другие типы прямоугольников имеют свои названия (ромб, квадрат, … Словарь слов.
Параллелограмм — а, м. параллелограмм м. и лт; лат. и лт; гр. parallelogrammon. 1. мат. Четырехугольник, у которого все стороны попарно параллельны. ABC 1. Неравнобедренный четырехугольник называется прямоугольником и дан в качестве диагонали. Арифметика. Магне. 214.//Сл. 186… Исторический словарь русского языка.
ПАРАЛЛЕЛЬ — Четырехугольник с попарно параллельными сторонами, от греческого parallels (параллельные и грамматические линии). Специальные типы прямоугольника: прямоугольники, прямоугольники, прямоугольники, прямоугольники, прямоугольники, прямоугольники, прямоугольники, прямоугольники, прямоугольники. Прямоугольник — это прямоугольник и все его углы правильные — Ромб — это прямоугольник и все его стороны равны — … Энциклопедический словарь.
Параллелограмм — Словарь русских синонимов для прямоугольника, квадрата, ромба, четырехугольника, ромба. -Ромбический словарь русских синонимов. Box 5.0. 2012… Словарь синонимов.
Прямоугольник — четырехугольник (плоская форма четырехугольника), в котором каждая пара противоположных сторон параллельна. Прямоугольник имеет равные и противоположные стороны и углы. Площадь прямоугольника равна произведению одной … Словарь научных энциклопедий.
PARALLELOGRAM-PARALLELOGRAM, параллелограмм, супруг. (греч. широта, широта и широта, из надписи) (Мат.). Четырехугольник, противоположные стороны которого одинаково параллельны. Как найти параллелограмм (геом.) ❖ силы или скорости. …… Словарь Усакова.
PARALLELOGRAM-PARALLELOGRAM, a, муж. В математике: четырехугольник, стороны которого парные и параллельные. Словарь Ожегова. С. Ожегов, Н. Шведова. 19491992… Словарь Ожегова.
Прямоугольник — четырехугольник, каждая пара его противоположных сторон параллельна и … Энциклопедия Брокгауза и Ефрона.
Прямоугольник — это двумерная геометрическая фигура, противоположные стороны которой взаимно параллельны. Это может быть: квадрат, прямоугольник, ромб … Большая энциклопедия промышленного колледжа.
Параллелограмм — а; м. от греч. parallēlos параллельный и grammē линия мата. Четырехугольник, противоположные стороны которого параллельны. Чтобы построить, нарисуйте p. П. (специальная геометрическая структура, выражающая закон сложения сил). * *** Прямоугольники …… Энциклопедический словарь.
Мы постоянно совершенствуем это руководство, и вы можете помочь нам в этом. Доступ и использование пособия «Юклава» без ограничений (более 100 статей по всем темам ЕГЭ и ОГЭ, более 2000 решенных задач, более 20 вебинаров и обучающих пособий)
Параллелограмм
Прямоугольники — это параллельные четырехугольники с попарно противоположными сторонами. Площадь прямоугольника равна произведению его основания (a) на высоту (h). Вы также можете найти его площадь по двум сторонам и углам, а также по диагоналям.
Квадраты, прямоугольники и ромбы являются разновидностью прямоугольника (частный случай).
Свойства параллелограмма
1. Противоположные стороны тождественны
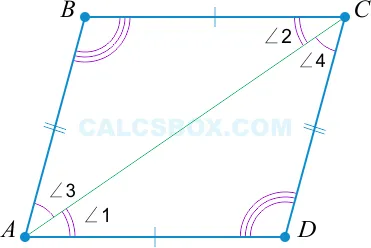
Первое, что необходимо сделать, это провести диагональ Lo_AC \ Вы получите два треугольника, \(ABC \) и \(ADC \).
Если \(ABCD \) — прямоугольник, то применимо следующее.
\(AD || BC \ стрелка вправо \угол 1=\угол 2\) как перекрестный текст.
\(AB ||CD \ правая стрелка \угол3=\ угол4\) как бы пересекаются.
Следовательно, Ј(Ј треугольник ABC = Ј треугольник ADC Ј) (согласно второму принципу: Ј(Ј угол 1 = Ј угол 2, Ј угол 3 = Ј угол 4 Ј) и Ј(AC \) — общие).
Так, \(⌘ треугольник ABC = ⌘ треугольник ADC ⌘), тогда \(AB = CD \) и \(AD = BC \).
2. Противоположные углы тождественны
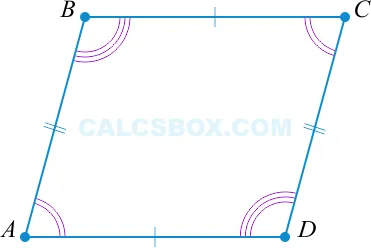
Согласно доказательству свойства 1, мы видим, что ⌘ (⌘ угол 1 = ⌘ угол 2, ⌘ угол 3 = ⌘ угол 4 ⌘). Поэтому сумма противоположных углов равна: \(\ угол1 +\ угол3 =\ угол2+\ угол4\). Если \(\треугольник ABC =\треугольник ADC\), то \(\угольник A =\угольник C\) и \(\угольник B =\угольник D\).
3. Диагонали разделены пополам точкой пересечения
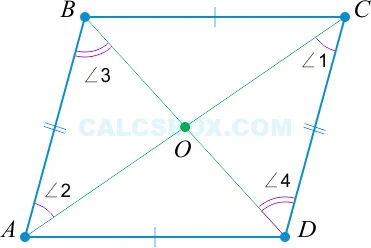
Из свойства 1 следует, что противоположные стороны одинаковы: \(AB =CD \). Еще раз обратите внимание на равные углы, которые пересекаются.
Таким образом, мы видим, что \(⌘ треугольник AOB = ⌘ треугольник COD ⌘) имеет второй признак равенства треугольников (двух углов и стороны между ними). То есть, \(BO = OD \) (противоположные углы \(\ угол 2 \) и \(\ угол 1 \)) и \(AO = OC \) (противоположные углы \(\ угол 3 \) и \(\ угол 4ዄ) соответственно).
Признаки параллелограмма
Если проблема имеет только один атрибут, то фигура является прямоугольником, и все свойства этой фигуры могут быть использованы.
Чтобы лучше запомнить, обратите внимание, что свойства прямоугольника отвечают на следующий вопрос — «Откуда я знаю?».. Другими словами, откуда вы знаете, что определенная фигура является прямоугольником?
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
\(AB = CD \); \(AB || CD\ правая стрелка ABCD\) — прямоугольник.
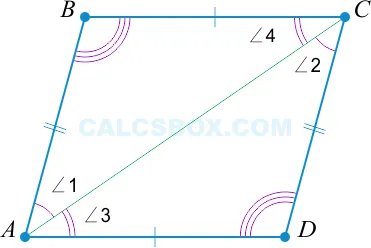
Посмотрите внимательнее. Почему \(AD || BC \|)?
\Согласно ዤ(ዤ треугольник ABC = ዤ треугольник ADC ዤ) свойству 1: ዤ(AB = CD \), ዤ(ዤ угол 1 = ዤ угол 2ዤ)ዤ(AB \) и ዤ(CD \) параллельны и ዤ(AC \) квадратичны.
Однако для 섹 (섹 треугольник ABC = 섹 треугольник ADC 섹), 섹 (섹 угол 3 = 섹 угол 4) (섹 (AD || BC \) и 섹 (섹 угол 3 \) также являются перекрестно эквивалентными).
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
\(AB = CD \) и Ј(AD = BCЈ правая стрелка ABCDЈ) — прямоугольники.
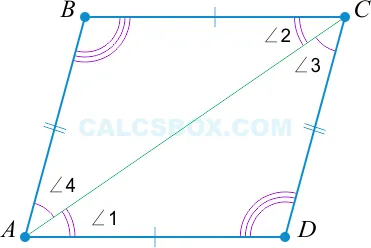
Рассмотрите этот знак. Еще раз проведите диагональ ⌘ (AC \).
По свойству 1 ⌘ (⌘ треугольник ABC = ⌘ треугольник ACD ⌘).
Поэтому ἀ(ἀ угол 1 = \ угол 2 \ Прямоугольник AD || BC \) и ἀ(ἀ угол 3 = \ угол 4 \ Прямоугольник AB || CD \), то есть ἀ(ABCD \), являются прямоугольниками.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
\ᢙ (ᢙ угол A = ᢙ угол C) и ᢙ (ᢙ угол B = ᢙ угол D ᢙ прямая стрелка ABCD) являются прямоугольными.
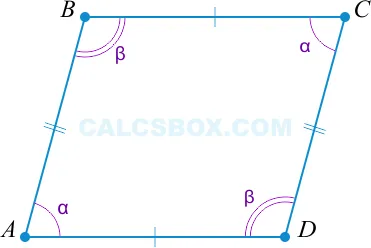
\(2 \ альфа + 2 \ бета = 360 ^ \) (⌘(⌘ угол A =⌘ угол C⌘), поэтому ⌘(⌘ угол B =⌘ угол D⌘) по условию).
\(⌘).(⌘).(⌘).(⌘).(⌘). Однако, ᢙ(ᢙ альфа \) и ᢙ(ᢙ бета \) являются односторонними в рамках вторичного ᢙ(AB \).
Тот факт, что 슰(슰 альфа + 슰 бета = 180 ^ \) также указывает на то, что 슰(AD || BC \).
Поэтому 슰 (슰 альфа \) и 슰 (슰 бета \) являются односторонними внутри вторичного 슰 (AB || CD \).
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
\ (AO = OC \); \ (BO = OD \ стрелка вправо ɛ) прямоугольник.
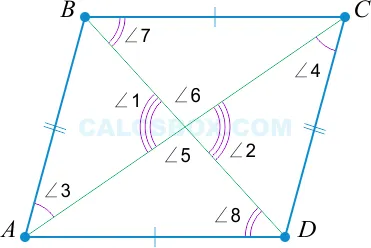
\(BO = OD \); \(AO = OC \); \(⌘ Угол 1 = ⌘ Угол 2) как перпендикуляр; \(⌘ Правая стрелка ⌘ треугольника AOB = ⌘ Треугольник COD ⌘); \(⌘ Правая стрелка ⌘ Угол 3 = ⌘ Угол 4); и ⌘(⌘ Правая стрелка AB || CD \).
Аналогично Ј(BO = OD \); Ј(AO = OC \), Ј(Ј угол 5 = Ј угол 6 Ј треугольник с прямыми стрелками AOD = Ј треугольник BOC Ј угол 7 = Ј угол 8 Ј) и Ј(ЈΔεξίβέλος AD || BC \).








