Две прямые пересекаются, и второй порядок образует восемь непересекающихся углов. Чтобы сформулировать необходимые и компетентные условия, мы используем такие типы углов, как диагонали, соответствующие углы и односторонние углы. Давайте покажем их в картинках:.
Что такое параллельная прямая
Такие «теоремы», которые помогают нам заложить основы и не требуют доказательства, называются аксиомами (от греч. axioms — «утверждения»).
Аксиомы — это утверждения, которые в науке считаются истинными без доказательств и используются для доказательства других утверждений (теорем).
Зачем в геометрии нужны аксиомы?
Вспомните доказанную ранее теорему о смежных углах: «Сумма смежных углов равна $ 180^$».
Поэтому смежные углы образуются при пересечении двух прямых. Поэтому без определения прямой линии не обойтись. Другими словами, прямая линия всегда прямая, не прерывистая и нигде не изгибается. Во-вторых, необходимо понимать, что две линии могут иметь только одну точку пересечения. В-третьих, мера градуса развернутого угла состоит в том, что он представляет собой сумму мер углов, деленную на лучи.
‘Сумма смежных углов…’ для формулировки фразы «сумма смежных углов…» требовалось ввести не менее трех утверждений на бездоказательной основе. В общем, каждая теорема разбивается на более мелкие «части», которые не нужно доказывать.
Основные аксиомы геометрии
Конечно, родоначальником геометрических основ был Евклид. Он первым сформулировал основные аксиомы геометрии как науки об элементах и дал фундаментальные определения, которые, хотя и частично измененные, сохранились до наших дней. Таково, например, древнее определение параллельных прямых.
Для удобства запоминания принято разделять основные аксиомы на следующие пять групп
- принадлежности;
- расположения;
- откладывания;
- измерения;
- аксиома параллельности .
Некоторые полезные мнемоники

Из первой буквы аксиомы можно построить слово PIROP. Пемза — это небольшой камень, похожий по цвету на гранат. В качестве акронима это может быть ‘π-аффилиация’, ‘θ-измерение’, ‘π-аранжировка’, ‘ο-дефференциация’ или ‘π-параллельная обработка’.
Параллелизм занимает последнее место, потому что это единственная группа, которая содержит только одну аксиому. Поэтому, помимо запоминания групп аксиом, вы пополняете свой словарный запас интересными словами о минералах.
Многие из них интуитивны и поэтому не «обрамлены», но косвенно упоминаются на уроках геометрии.
Например, при изучении точек и линий мы упоминали, что точка может принадлежать или не принадлежать линии. Действительно, это одна из аксиом принадлежности. «Чем бы ни была линия, есть точки, которые ей принадлежат, и точки, которые ей не принадлежат».
Аксиома параллельности
Аксиома параллелизма. Существует только одна прямая, параллельная данной прямой, которая проходит через точку, не лежащую на данной прямой.
Проведем на плоскости прямую $a$ и отметим точку $F$, которая не лежит на прямой $a$. Согласно аксиоме параллельности, через $F$ может проходить только одна прямая, параллельная прямой $a$. Обратите внимание на линию $B$ на диаграмме.
В самом деле, если через точку $ F $ провести другую прямую, прямую $ b_1 $, то она не будет совпадать с прямой $ b $. Если продолжить линию, то точки $ a $ и $ b_1 $ пересекутся.
Заключение на строке $ b_1 $ формально не считается доказательством. Несмотря на сложность формулировки, предложение об уникальности параллельных линий воспринимается как само собой разумеющееся.
Параллельные прямые — это прямые, которые лежат в одной плоскости и не пересекаются, сколько бы раз их не продолжали: ɑ (ɑ displaystyle a \ parallel b \).
Параллельные прямые
Параллельные (и в некоторых случаях эквивалентные) прямые — это прямые, лежащие в одной плоскости и не совпадающие и не пересекающиеся. В определениях некоторых школ одновременные линии не считаются параллельными, поэтому такие определения здесь не учитываются.
Свойства
- Параллельность — бинарноеотношение эквивалентности, поэтому разбивает всё множество прямых на классы параллельных между собой прямых.
- Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две)
- 2 параллельные прямые в пространстве лежат в одной плоскости.
- При пересечении 2 параллельных прямых третьей, называемой секущей :
- Секущая обязательно пересекает обе прямые.
- При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Накрест лежащие углы равны.
- Соответственные углы равны.
- Односторонние углы в сумме составляют 180°.
В геометрии Лобачевского
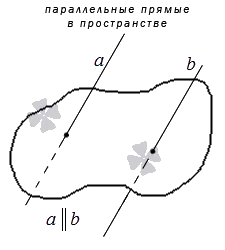
Параллельные прямые в модели Пуанкаре: две зеленые прямые параллельны синей прямой, а фиолетовая прямая гиперпараллельна ей.
Уравнение нельзя анализировать в геометрии Лобачевского на уровне через определенную точку (лексическая ошибка): c За пределами линии AB
Линия CE называется эквидистантной (параллельной) линии A B в направлении от A к B.
- точки B и E лежат по одну сторону от прямой A C ;
- прямая C E не пересекает прямую A B , но всякий луч, проходящий внутри угла A C E , пересекает луч A B .
Линии AB — B также определяются как равноудаленные от AB в направлении от B к A.
Все остальные прямые, которые не пересекаются с данной прямой, называются гиперпараллельными или расходящимися.
См. также
Фонд Викимедиа. 2010.
Полезное
Смотреть что такое «Параллельные прямые» в других словарях:
ПАРАЛЛЕЛЬНЫЕ ряды — ПАРАЛЛЕЛЬНЫЕ ряды, непересекающиеся линии на одном уровне… Современная энциклопедия.
ПАРАЛЛЕЛЬНЫЕ ряды — пересекающиеся линии на одном уровне… Большой энциклопедический словарь
Параллельные линии — ПАРАЛЛЕЛЬНЫЕ СТРОКИ, непересекающиеся линии, которые находятся на одном уровне. …. Иллюстрированный энциклопедический словарь
Параллельные прямые — в евклидовой геометрии прямые, лежащие в одной плоскости и не пересекающиеся. В абсолютной геометрии (см. абсолютная геометрия), из точки, не лежащей на данной прямой, проходящей хотя бы через одну прямую, не пересекающую данную прямую. В: ……. Советская энциклопедия.
Параллельные прямые — это непересекающиеся прямые на одной плоскости. * * * * ПАРАЛЛЕЛЬНАЯ ЛИНИЯ ПАРАЛЛЕЛЬНАЯ ЛИНИЯ, линия, не пересекающаяся на плоскости … Энциклопедический словарь.
ПАРАЛЛЕЛЬНАЯ ЛИНИЯ — в евклидовой геометрии все линии лежат в одной плоскости и не пересекаются. В абсолютной геометрии существует по крайней мере одна линия, которая не пересекает данную линию. В евклидовой геометрии существует только один. …… Энциклопедия математики.
Параллельные прямые — прямые, которые пересекаются и не лежат в одной плоскости. Энциклопедический словарь.
Параллельные миры в научной фантастике — Эта статья может содержать оригинальное исследование. Добавьте ссылку на источник. В противном случае она может быть удалена. Дополнительную информацию можно найти на странице обсуждения. Это… Википедия.
Параллельные миры — Параллельный мир (воображаемый) — это реальность, которая существует в какой-то форме в то же время, независимо от нас. Размер этой автономной реальности может варьироваться от небольшой географической области до всей Вселенной. В то же время… Википедия.
Если ни параллельные прямые, ни их продолжения не пересекаются, прямая называется P. Одна ветвь этих линий равноудалена от другой. Однако говорят, что две прямые P пересекаются в бесконечности. Это… Энциклопедия Брокгауза и Ефрона.
Ответ на первый вопрос называется «свойства параллельных прямых», а ответ на второй вопрос — «точки параллельных прямых».
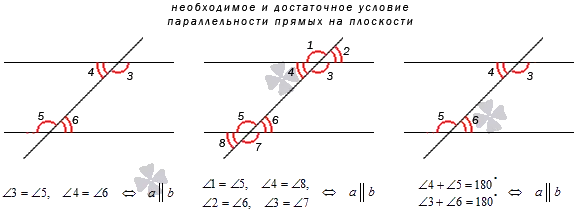
Типы углов при параллельных прямых
Когда прямая пересекает две другие прямые, параллельные друг другу, образуется восемь углов. В геометрии они имеют свое название и свойства. Для дальнейшего изучения темы этой статьи достаточно разобраться в трех типах. Затем посмотрите на следующую диаграмму при рассмотрении каждого из них в отдельности.
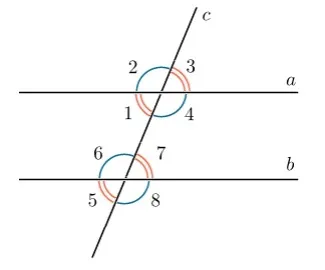
Односторонние
На диаграмме выше это углы 1, 6, 4 и 7. Они находятся на одной стороне по отношению к прямой линии.
Соответственные
Углы 2 и 6, 3 и 7, 1 и 5, 4 и 8.
Накрест лежащие
На этой схеме ρ3 и ρ5, ρ2 и ρ8, ρ1 и ρ7, ρ4 и ∠6. Их расположение легко запомнить, потому что они пересекаются.
Условия параллельности
Чтобы доказать параллельность прямой, он должен знать точку, которую нужно определить. Достаточно хотя бы одного из следующих условий
Накрест лежащие углы равны
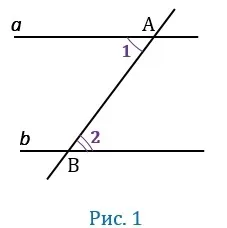
Дано: ǫ(a \; \ vert b \), ab — квадратичный, а углы 1 и 2 — трансверсальные.
Доказательство: предположим, что ¶1 и ∠2 не равны. Тогда, если мы нарисуем углы PAB, то они являются крестообразными соседями ¶2.
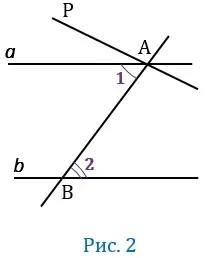
Поперечные углы равны. Это выглядит как ap \(ɑ vert \ vert)b. Однако это невозможно. Поскольку, согласно Бюро, из точки A может пройти только одна прямая, существует две прямые — B и A. H.T.
Соответственные углы равны
∠1 и ∠2 соответствуют друг другу.
mn \(슰 vert vert)ad. докажите, что \(슰 angle nmc = \ angle bad \).
Решение: DŽ (DŽ угол nmc = \ угол dac \) (соответствующий) и DŽ (DŽ угол dac = \ угол bad \) (ad — биссектриса). Следовательно, 섹 (угол nmc = \ угол плохой \).
Сумма односторонних углов равна 180 градусов
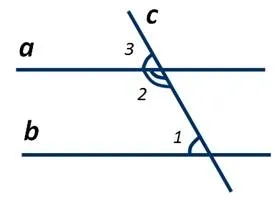
a \ (ˉ vert \) b, следовательно, ρ1 = ρ3 (соответственно). 2+∠3=180º (прилегание). Поэтому сложение приводит к 180º.
Если обе прямые параллельны третьей
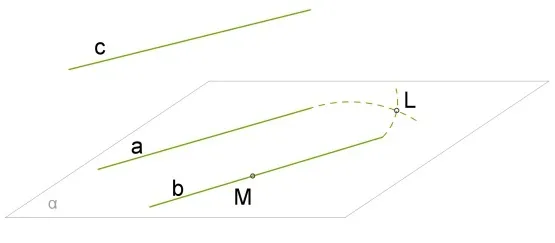
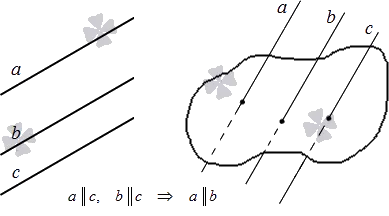
Это также называется теоремой о трех параллельных линиях уровней. a \ (섹 vert \ vert) b и c \ (섹 vert) b, где a \ (섹 vert) c.
\Тут есть \ (섹 vert \ vert \ vert \)b. Предположим, что существует еще одно c \(\ vert \ vert \ vert \)a. По договору, a не пересекает b и наоборот.
В трехмерном пространстве прямые, параллельные третьей, параллельны друг с другом
Это то же самое, что и предыдущий элемент: если a и c || то b и c тоже ||, a и b тоже ||.
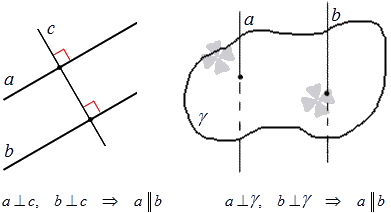
Две прямые, перпендикулярные третьей, параллельны

Символика вертикальной прямолинейности: ⊥
На рисунке видно, что a \(⌘ perp \)c и b \(⌘ perp \)c. Поэтому, согласно теореме о точке, она имеет вид \(⌘ perp \)b
Предположим, что a \(⌘ perp \)c и b \(⌘ perp \)c, но a не ⌘(⌘ vert \; \)b. Далее, в какой-то точке a и b пересекаются. Подумайте о треугольнике ABC. Сумма его углов будет равна 180º + ∠C. Но это не может быть так. Следовательно, наш случай неверен и ⌘(⌘ vert \ vert \}b.
Доказательство параллельности прямых
Ниже приводится доказательство теоремы из первой части работы.
- Есть a (прямая) и М (точка, далее — т.). Она не принадлежит a. Через них проходит плоскость альфа ( \(\alpha\) ). Известно, она единственная.Прямая b проходит через т.М и \(\vert\vert\;\) а. Она существует, что доказывает аксиома о \(\;\vert\vert.\)
- Предположим, что существует прямая с, которая тоже проходит через т.М, причем c \(\vert\vert\) a. В этом случае потребуется другая плоскость \(\beta\), такая, чтобы прошла через т.М. Такое невозможно, потому что есть теорема, которая говорит, что плоскость только одна. Значит это одна и та же плоскость ( \(\alpha\) совпала с \(\beta\) ) и одна и та же прямая (b совпал с c). Единственность прямой доказана.
Следовательно, вектор перпендикулярен. Это свидетельствует о необходимом и грамотном выполнении договора о параллельности исходных линий. Другими словами, эти линии параллельны.
Параллельность прямых

Если в задаче есть параллельные прямые, это большие деньги, потому что это дает много равных углов, под которыми можно рассчитать почти все. Далее мы рассмотрим другие бонусы, которые предлагают параллели, и то, как они помогают в решении проблемы.
Определение параллельности прямых
Начнем с главного — определения того, какие прямые являются параллельными в соответствии с геометрией Евклида. Мы не упоминаем Эвклида без причины. Это связано с тем, что первое упоминание о параллелизме дошло до нас в его трудах, написанных за 300 лет до Рождества Христова.
Линия, даже если ее продолжить в бесконечность, параллельна, так как не имеет пересечения. Это показано следующим образом: a ii b.
Все кажется простым, но со времен Евклида лучшие умы спорили об определении параллельных прямых и свойствах параллельности прямых. Пятый кабинет древнегреческих математиков был особенно интересен. Через точку могут проходить только прямые, параллельные первой прямой. В 19 веке русский математик Н. Лобачевский опроверг это положение и показал условия, при которых из одной точки могут проходить как минимум две параллельные прямые.
Однако, поскольку школьная программа ограничена евклидовой геометрией, вышеприведенное утверждение принимается как аксиома.
На плоскости простая прямая не принадлежит прямой и может проходить через любую точку, параллельную прямой.
Онлайн-уроки математики Skysmart помогут вам улучшить свои оценки и подготовиться к экзаменам, IEP и тестам.
Свойства и признаки параллельных прямых
Существует несколько точек, по которым можно определить, параллельна ли одна прямая другой. К счастью, нет необходимости запоминать много информации, поскольку свойства линии и широтной линии тесно связаны.
Давайте начнем со свойств. Для этого проведите третью линию, пересекающую параллельную линию. Это называется вторичной линией. Следовательно, существует восемь углов.
Если вторичная прямая проходит через две параллельные прямые, то
-
два внутренних односторонних угла образуют в сумме 180°:
Если вторичная образующая перпендикулярна одной из параллельных прямых, то она также перпендикулярна и другой.
Указанное свойство одновременно является точкой, из которой можно вывести параллельность прямых. И пока выявлен и доказан только один признак, с ним могут быть связаны другие признаки.
Давайте теперь посмотрим, как все эти свойства помогают решить задачу, и потренируемся в определении параллельности двух прямых.
Задача 1
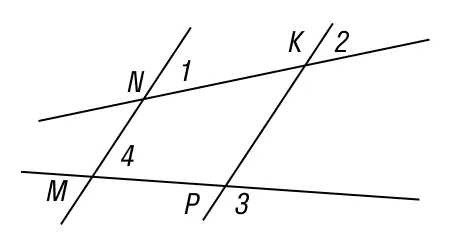
Линии MN и KP пересекают две другие линии и образуют разные углы. Известно, что ∠1 = 73°, ∠3 = 92° и ∠2 = 73°. Необходимо найти значение ∠4.
В данном случае ∠3 и ∠MPK перпендикулярны, поэтому ∠MPK=∠3=92°.
Поскольку ∠1 и ∠2 соответственно, их равенство указывает на то, что они являются МНИИКП.
Согласно другому свойству параллельных прямых, ∠4+∠MPK=180°.
Задача 2
Две параллельные прямые α и β находятся на расстоянии 27 см друг от друга. Квадратик этих линий образует с одной из них угол 150°. Найдите значение отрезка между a и b.
II b, поэтому ∠MKD+∠KDN=180°.
Therefore, ∠MKD=180°-∠KDN=180°-150°=30°.
Далее рассмотрим треугольник KDM. Мы знаем, что DM — это расстояние между a и b, поэтому DM┴b и треугольник — прямой угол.
Катетер с другой стороны угла 30° составляет 1/2 косой стороны, поэтому DM =1/2DK.
Параллельность является достаточным условием для обеспечения параллельности прямых. Другими словами, выполнение этого условия достаточно для доказательства параллелизма.
Что такое параллельные прямые
Параллельные прямые — это прямые, которые не пересекаются.
В этом определении параллельных линий есть небольшая неточность. Линии, имеющие несколько общих точек, конгруэнтны. Иногда их называют параллелями.
Линии, пересекающие параллельные прямые, называются вторичными. Пересекающиеся линии образуют восемь углов. По отношению друг к другу они могут соответствовать и пересекаться в одностороннем порядке. Давайте рассмотрим их в качестве примера.
- Соответственные углы: 7 и 2, 1 и 6, 8 и 4, 3 и 5
- Накрест лежащие: 7 и 5, 8 и 6, 1и 4, 3 и 2
- Односторонние: 1и 2, 3 и 4, 7 и 6, 8 и 5
Аксиома параллельных прямых
Аксиома о параллельных прямых является одним из фундаментальных положений геометрии. Через точку можно провести прямую, параллельную определенной точке, и только через одну из них. Это наиболее распространенная формулировка аксиомы.
Аксиома имеет два следствия.
- Если прямая параллельна одной из двух параллельных прямых, то она параллельна и второй.
- Если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.
Обратите внимание, что аксиома применима только к уровням. В пространстве изменение может происходить, когда линия параллельна плоскости. В этом случае существует бесконечное множество параллельных прямых, проходящих через одну точку. Поэтому условие не всегда выполняется в этот период.
Расстояние между параллельными прямыми в любой данной точке одинаково и равно величине отрезка, перпендикулярного каждой прямой.
Фигуры с параллельными прямыми
Существует множество фигур, которые можно сформировать с помощью параллельных прямых. Например, прямоугольник состоит из двух пар параллельных отрезков.
Квадраты и прямоугольники также состоят из пар параллельных линий, но являются частным случаем прямоугольников.
В треугольнике средняя линия всегда параллельна основанию.
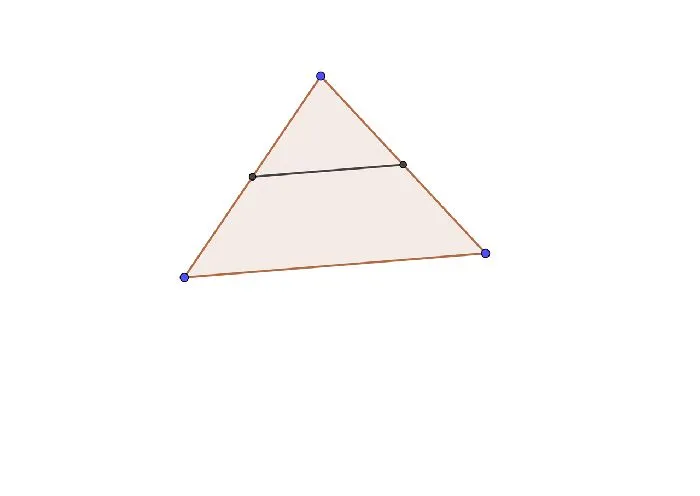
Рисунок 2: Средняя линия треугольника.
Есть еще одна интересная форма: трапеция. В столе большое и малое основания параллельны друг другу, а боковые стороны — нет.
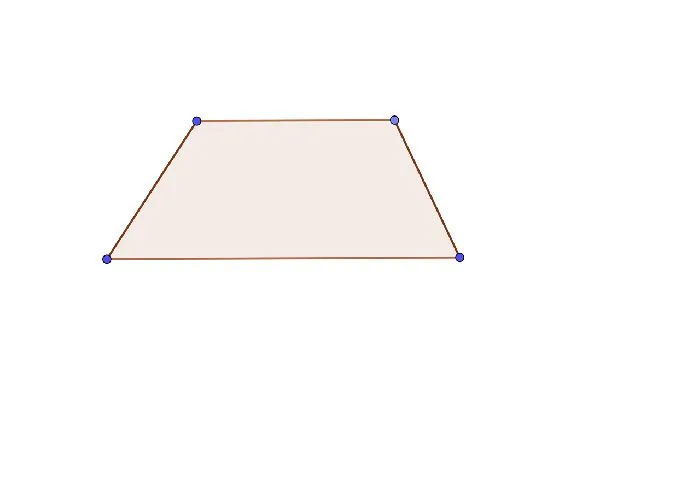
Рис. 3. Трапеция.
Если прямые не параллельны, то они пересекаются, но если отрезки не параллельны, то они не пересекаются. Поскольку значения длины отрезков конечны, отрезки отделяются только друг от друга. Тем не менее, отдельных типов или таблиц параллельных линий не существует, и их появление маловероятно.








