Пирамида — это многоугольникгранник, одна грань из которых (основание) является многоугольником, а другой грани (стороны) — это треугольники, имеющие общую вершину.
Урок 31. Прямоугольный параллелепипед
Прямоугольный параллелепипед – это шестигранник, у которого все грани имеют прямоугольную форму.
Лицо — это плоская поверхность предмета, образующая угол с другой поверхностью. такой же поверхностью.
Основания параллелепипеда — верхний и нижний грани.
Обязательное чтение
Никольский С. М. Математика. 5 класс. учебное пособие для общеобразовательных учреждений // С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др. — М.: Просвещение, 2017 г. — 272 с.
Дальнейшее чтение
1. математика: тематические тесты. П.В. Чулков, Е.Ф. Шершнев, О.Ф. Зарапина.
Шарыгин И. Ф. Задачи на пригеклку: 5-6 класс // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014 г. — 95 с.
Теоретический материал для самостоятельного изучения
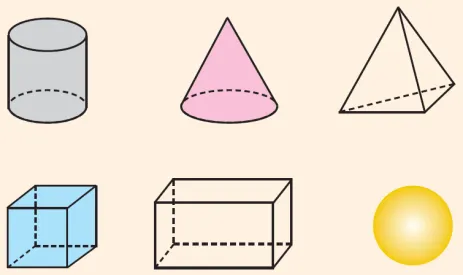
Мир, в котором мы живем, состоит из огромного количества предметов разных форм, цветов и размеров. Исследование их свойства, Люди открывают для себя что-то новое. Например, математики изучают геометрические твердые тела в окружающей среде: цилиндры, кубы. и так далее.
Сегодня мы рассмотрим прямоугольник параллелепипед – многогранник, название которого переводится с древнегреческого как «самолеты, летящие бок о бок».
Прямоугольный параллелепипед ограничОн состоит из шести прямоугольников, а именно. гранями. Край, на котором располагается прямоугольник. параллелепипед, Край прямоугольника и его противоположность называются нижней и верхней ножкой.
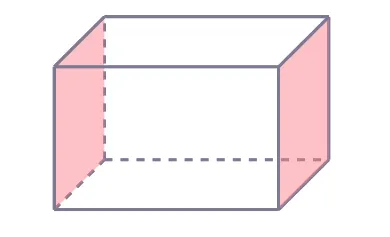
Остальные четыре грани называют боковыми гранями.
Стороны граней параллелепипеда называются ребрами. Их двенадцать.
Концы ребер называются вершинами. К ним относятся. в параллелепипеде восемь.
Вершина — это общая точка трех ребер.
Длины двух ребер базовой поверхности, начиная от вершины, называются длиной и шириной прямоугольника. параллелепипеда.
Длина боковой грани называется высотой.
Таким образом, длины трех ребер, начиная от вершины, называются длиной, шириной и высотой. В противном случае длина, ширина и высота называются размерами прямоугольника параллелепипеда.
Прямоугольный параллелепипед, который имеет три равные грани, начинающиеся от вершины, называется кубом. Каждый грань куба – квадрат.
Рассмотрим свойства прямоугольного параллелепипеда и куба.
У прямоугольного параллелепипед а противоположные грани равны.
Все грани куба равны между собой.
Построим прямоугольник с заданной длиной a и высотой h.
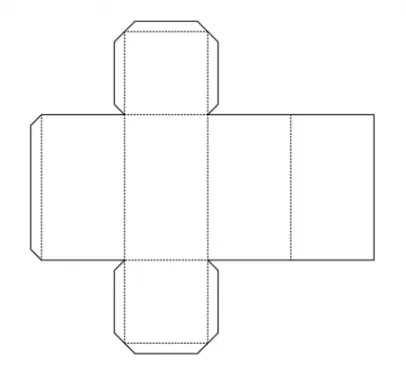
Из каждой вершины добавьте отрезок длиной, равной половине ширины b, под углом 45 градусов. И соедините концы отрезков, невидимые. грани – пунктирной линией.
Изготовить параллелепипед Существует несколько вариантов. Например, с помощью дрели. Нарисуйте на бумаге шаблон, похожий на шаблон выше. Обратите внимание, что на рисунке припуски на швы даны с учетом возможности сварки. параллелепипед.
Пирамида — это многоугольникгранник, одна грань из которых (основание) является многоугольником, а другой грани (стороны) — это треугольники, имеющие общую вершину.
Параллелепипед и его свойства
Параллелограмм из параллелепипед, называются его гранями, их стороны являются ребрами, а вершины параллелограммов — вершинами. параллелепипеда. У параллелепипеда все грани — параллелограммы.
Параллелограммы, как и все призмы, могут быть прямыми и косыми.
Принято различать две противоположные грани базы и называть их базами, а остальные грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, которые не принадлежат основаниям, называются боковыми ребрами.
Две грани параллелепипеда, Те, которые имеют общий край, называются смежными, а те, которые не имеют общего края, называются противоположными.
Часть, соединяющая две вершины, которые не принадлежат к одному и тому же грани, называется диагональю параллелепипеда.
Прямой параллелепипед, основанием которого является прямоугольник, называется прямоугольником. параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.
Длины непараллельных ребер прямоугольника параллелепипеда называются линейными измерениями (мерами). Прямоугольник имеет параллелепипеда три линейных измерения.
Свойства параллелепипеда:
· Противоположные грани параллелепипеда Они равны и параллельны.
— Все четыре диагонали параллелепипеда пересекаются в точке и делятся этой точкой на две половины.
· Боковые грани прямого параллелепипеда — прямоугольники.
— Квадрат диагонали прямоугольника параллелепипеда равна сумме квадратов трех его диаметров.
Принято различать две противоположные грани базы и называть их базами, а остальные грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, которые не принадлежат основаниям, называются боковыми ребрами.
Параллелепипед
Призма называется параллелепипедом. если его основания являются параллелограммами. См. рисунок 1.
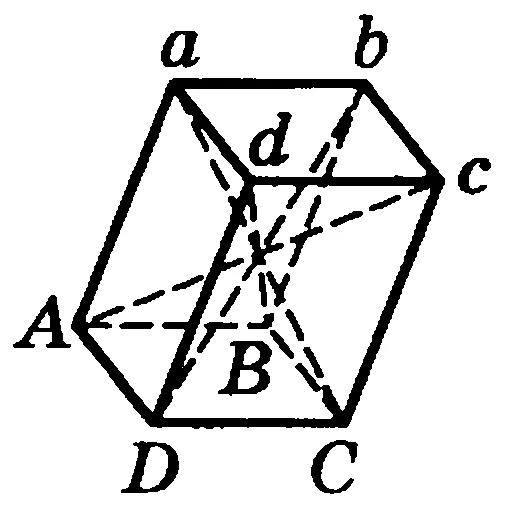
Смежные грани параллелепипеда – две грани,. которые имеют общий край.
Противоположные грани параллелепипеда – грани,. без общего края.
Противоположные вершины параллелепипеда — две вершины, которые не принадлежат к одному и тому же грани.
Диагональ параллелепипеда — отрезок, соединяющий противоположные вершины.
Когда боковые грани перпендикулярны плоскостям оснований, то параллелепипед называется прямым .
Прямой параллелепипед, основания которых ортогональны, называется прямоугольником. Призма все грани Основание которого — квадрат, называется кубом.
Параллелограмм — это призма, основания которой являются параллелограммами.
Прямой параллелепипед – параллелепипед, боковые грани которого перпендикулярны плоскости основания.
Прямоугольный параллелепипед – это прямой параллелепипед, основания которых — прямоугольники.
Куб — это прямоугольник. параллелепипед с равными ребрами.
Параллелограмм — это призма, основание которой является параллелограммом, таким образом, параллелепипед имеет шесть граней и все они являются параллелограммами.
Противоположные грани попарно равны и параллельны. Параллелограмм имеет четыре диагонали, которые пересекаются в одной точке и делятся посередине. Основание может быть любым квадратом. граньОбъем равен произведению основания и высоты.
Параллелограмм, четыре стороны которого являются прямоугольными грани называются прямыми линиями.
Прямой параллелепипед, все шесть сторон которого граней — ортогональны, называется прямоугольником. См. рис. 2.
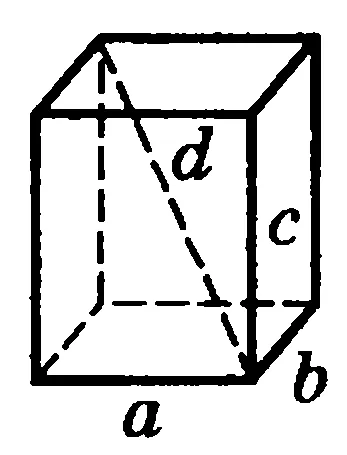
Объем (V) прямого параллелепипеда равна произведению площади основания (S) и высоты (h): V = Sh .
Для прямоугольного параллелепипеда, Более того, формула V = abc, где a,b,c — ребра.
Диагональ (d) прямоугольника параллелепипеда соединяется с его ребрами соотношением d 2 = a 2 + b 2 + c 2 .
Прямоугольный параллелепипед – параллелепипед, боковые грани которых перпендикулярны основаниям, а основания являются прямоугольниками.
Свойства прямоугольника параллелепипеда:
Квадрат диагонали прямоугольника параллелепипеда это сумма квадратов трех его диаметров (длины трех ребер, разделяющих вершину).
Прямоугольный параллелепипед, все грани Прямоугольник, имеющий форму квадрата, называется кубом. Все грани куба равны; объем (V) куба определяется по формуле V=a 3, где a — ребро куба.
Прямой параллелепипед, основанием которого является прямоугольник, называется прямоугольником. параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.
Прямоугольный параллелепипед

Они могут быть сделаны из разных материалов и разных цветов, но похожи по форме: коробки, шкафы, здания и т.д.
Площадь состоит из \(6\) прямоугольников, которые называются гранями прямоугольного параллелепипеда.
Две грани называются противоположными прямоугольниками, если они не имеют общего края. Каждые два противоположных прямоугольника называются противоположными прямоугольниками грани равны.
Вершины параллелепипеда — это вершины его граней, ребра — это отрезки, соединяющие вершины параллелепипеда.

Прямоугольный параллелепипед имеет \(8\) вершин, \(12\) ребер, \(6\) граней (спереди, сзади, снизу, сверху и с двух сторон),
Размеры прямоугольника параллелепипеда — являются его длина, ширина и высота (на рисунке ниже красные ребра с общей вершиной).

Если прямоугольник параллелепипеда все размеры равны, он называется кубом. Грани куба — это равные квадраты.
Прямой параллелепипед, основанием которого является прямоугольник, называется прямоугольником. параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.
Прямоугольный параллелепипед. Пирамида.
МногогранниK — это поверхность, состоящая из многоугольников. Края многоугольникагранниэто многоугольники, из которых состоит куб. Нет двух смежных граней грани многограннине находятся в одной плоскости. стороны граней — ребра многоугольникаграннии их концы являются вершинами многоугольника. На следующем рисунке показан многоугольник.гранники.
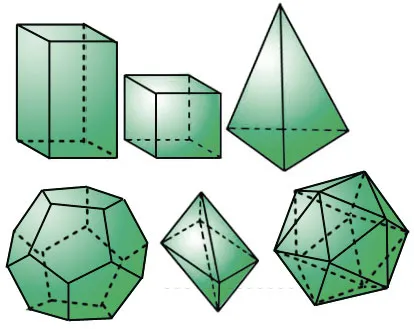
Один из самых простых мультипликаторовгранниэто прямоугольник. параллелепипед. Он состоит из шести прямоугольников, что означает, что его размер приблизительно .граничен шестью гранями.
ABCDA1B1C1D1 — прямоугольный параллелепипед. Концы прямоугольника параллелепипеда — это стороны граней (в нашем случае: AB, BC, CD, DA, A1B1 , B1C1 , C1D1 , D1A1 AA1 , BB1 , CC1 , ДД1 ), а его вершины являются вершинами граней (в нашем случае: A, B, C, D, A1 , B1 , C1 , D1 ), т.е. получаем, что прямоугольник имеет параллелепипеда 8 вершин и 12 ребер. Края прямоугольника параллелепипеда, которые не имеют общих вершин, называются противоположными ребрами (в нашем случае это пары: ABB1A1 и ДКК1D1 , ABCD и A1B1C1D1 , ADD1A1 и BCC1В1 ). грани параллелепипеда равны.
| Площадь поверхности параллелепипеда это сумма площадей всех его граней. |
Мера прямоугольника параллелепипеда — это длина трех ребер, имеющих общую вершину. Например, края BB1 , В1А1 , В1С1 размеры ABCDA1B1C1D1 :
Размеры имеют названия: Длина, ширина, высота. Мы используем эти названия, чтобы различать размеры:
Диагональ параллелепипеда — это отрезок, соединяющий две вершины, которые не принадлежат одному и тому же грани. Например, AC1 — Диагональ ABCDA1B1C1D1 :
Частный случай прямоугольника параллелепипеда является кубом. Куб — это прямоугольник параллелепипед, размеры которых одинаковы:








