Поскольку AT и MC — биссектрисы равных углов, ∠BAT = ∠BCM. ∠B является общим для ΔABT и ΔCBM. Поэтому ΔABT и ΔCBM равны со вторым знаком. Далее, AT=CM.
Основание треугольника

Основание треугольника — это та же сторона, что и две другие. Основание редко имеет какое-то особое значение, но его визуальное отделение от других сторон часто заставляет студентов путаться и делать ошибки. Давайте рассмотрим подробнее, как одна сторона треугольника может рассматриваться в качестве основания и какое значение она имеет в этом случае.
Стороны треугольника
Треугольник всегда имеет три стороны. Один из них считается базовым. Как правило, основание выделяется только структурой, то есть нижней стороной треугольника, который используется в качестве основания.
Иногда решение определяет угол основания любого треугольника. Это не совсем верно для произвольных треугольников, так как все углы равны. Поэтому не имеет смысла размечать углы у основания. Отмечаются только углы при основании равнобедренного треугольника.
Рисунок 1. Углы произвольного треугольника.
Следует помнить, что произвольные треугольники можно условно перевернуть, т.е. переделать фигуру так, чтобы противоположная сторона была основанием. Не имеет смысла разделять значение сторон и основания произвольного треугольника — это только внесет путаницу при решении задачи.
Уравнение основания треугольника и уравнение любой стороны треугольника является уравнением прямой линии.
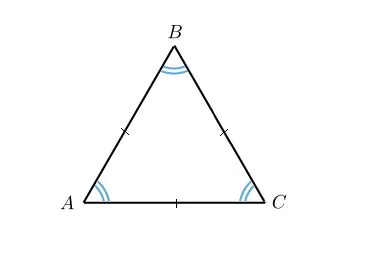
Равнобедренный треугольник
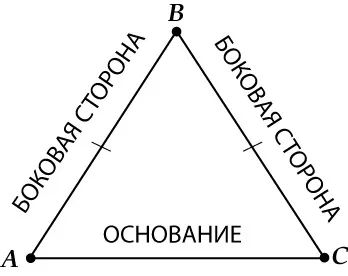
Равнобедренные треугольники — единственный вариант треугольника, в котором основание действительно значимо. Равнобедренный треугольник — это треугольник с двумя сторонами, равными друг другу. Равные стороны называются боковыми сторонами, а третья сторона — основанием.
Существуют две теоремы для основания равнобедренного треугольника. К ним относятся.
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.
В равнобедренном треугольнике основание определяется величиной боковых сторон. Равная сторона — это ребро, а неравная сторона — основание.
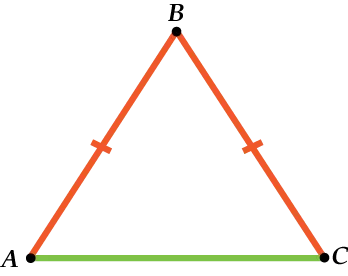
Рисунок 2. Равнобедренный треугольник.
В процессе решения задачи основание может оказаться поперечным. Не пугайтесь этого, так как основание может быть признано горизонтальным. Стоит привыкнуть к такому построению равнобедренных треугольников или каждый раз переделывать узор, направляя треугольники в нужную сторону.
Чтобы понять природу равнобедренных треугольников, нужно мыслить как равнобедренный треугольник, стать им и выучить четыре теоремы о его свойствах.
Стороны треугольника
Треугольник всегда имеет три стороны. Один из них считается базовым. Как правило, основание выделяется только структурой, то есть нижней стороной треугольника, который используется в качестве основания.
Иногда решение определяет угол основания любого треугольника. Это не совсем верно для произвольных треугольников, так как все углы равны. Поэтому не имеет смысла размечать углы у основания. Отмечаются только углы при основании равнобедренного треугольника.
Рисунок 1. Углы произвольного треугольника.
Следует помнить, что произвольные треугольники можно условно перевернуть, т.е. переделать фигуру так, чтобы противоположная сторона была основанием. Не имеет смысла разделять значение сторон и основания произвольного треугольника — это только внесет путаницу при решении задачи.
Уравнение основания треугольника и уравнение любой стороны треугольника является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренные треугольники — единственный вариант треугольника, в котором основание действительно значимо. Равнобедренный треугольник — это треугольник с двумя сторонами, равными друг другу. Равные стороны называются боковыми сторонами, а третья сторона — основанием.
Существуют две теоремы для основания равнобедренного треугольника. К ним относятся.
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.
В равнобедренном треугольнике основание определяется величиной боковых сторон. Равная сторона — это ребро, а неравная сторона — основание.
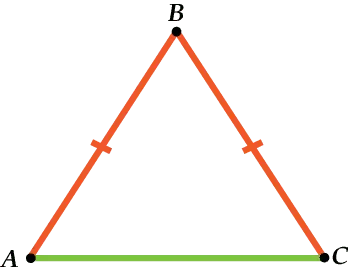
Рисунок 2. Равнобедренный треугольник.
В процессе решения задачи основание может оказаться поперечным. Не пугайтесь этого, так как основание может быть признано горизонтальным. Стоит привыкнуть к такому построению равнобедренных треугольников или каждый раз переделывать узор, направляя треугольники в нужную сторону.
Равносторонний треугольник
Равносторонние треугольники являются частным случаем равнобедренных треугольников. У равнобедренного треугольника две равные стороны, а у равностороннего — все три. Однако именно из-за этого свойства значение основания равнобедренного треугольника теряется.
Какая бы сторона равнобедренного треугольника ни была выбрана, две другие стороны всегда равны, поэтому любую из сторон можно считать основанием.
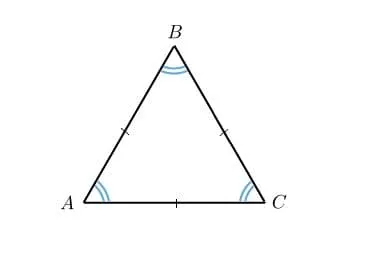
Рисунок 3. Равнобедренный треугольник.
Существует формула, на которую часто ссылается термин «база». Это формула площади, которая равна половине произведения основания на высоту, проведенную на основании треугольника. Однако за основу можно взять любую сторону, если это сторона, на которую приходится высота. Таким образом, даже в этом случае выбор сторон треугольника, который можно рассматривать как основание, неразличим.
В процессе решения задачи основание может оказаться поперечным. Не пугайтесь этого, так как основание может быть признано горизонтальным. Стоит привыкнуть к такому построению равнобедренных треугольников или каждый раз переделывать узор, направляя треугольники в нужную сторону.
Свойства равнобедренного треугольника
Чтобы понять природу равнобедренных треугольников, нужно мыслить как равнобедренный треугольник, стать им и выучить четыре теоремы о его свойствах.
Теорема 1: В равнобедренном треугольнике углы при основании равны.
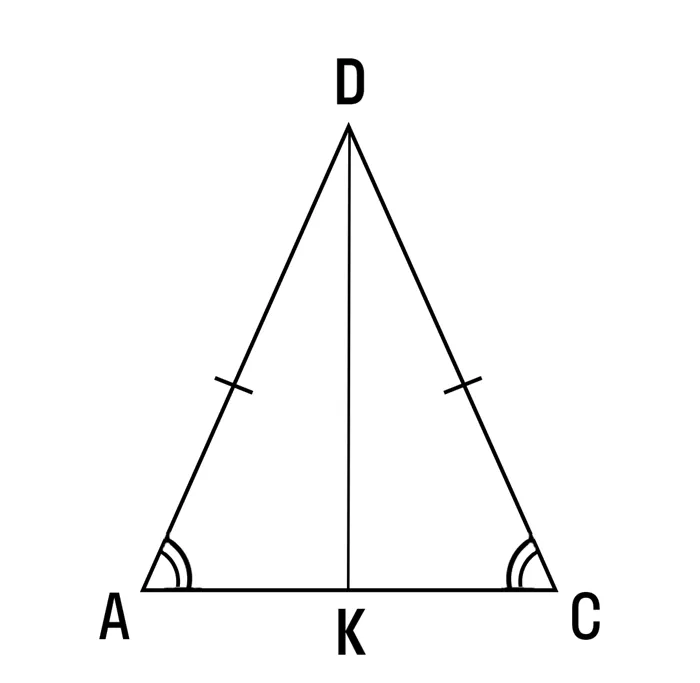
Пусть AC — основание равнобедренного треугольника. Постройте биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общий, а так как DK — биссектриса, угол ADK равен углу CDK). Поскольку треугольники равны, угол A равен углу C, так как все соответствующие элементы равны. Успокойся.
Теорема 2: В равнобедренном треугольнике биссектрисы, проведенные к основанию, являются медианой и высотой.
ΔABH = ΔCBH с обеих сторон и угол между ними (углы ABH и CBH равны, потому что BH — биссектриса, ΔABC — потому что это равнобедренный треугольник, AB = BC и BH — общая сторона).
Таким образом, во-первых, AH = HC, а BH — медиана.
Во-вторых, углы BHA и BHC равны и смежны. Это означает, что общая сумма составляет 180 градусов. Следовательно, она равна 90 градусам, а BH — это высота.
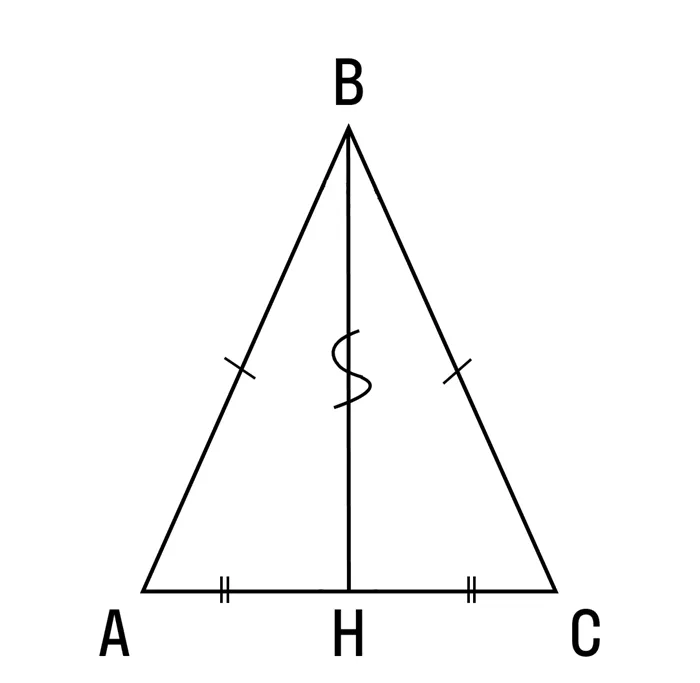
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
ΔABH = ΔCBH из трех сторон (AH = CH равны, так как BH — медиана, ΔABC — равнобедренный треугольник, AB = BC и BH — общие стороны).
Таким образом, во-первых, углы ABH и CBH равны, а BH является биссектрисой.
Во-вторых, углы BHA и BHC равны и смежны. Это означает, что общая сумма составляет 180 градусов. Следовательно, она равна 90 градусам, а BH — это высота.
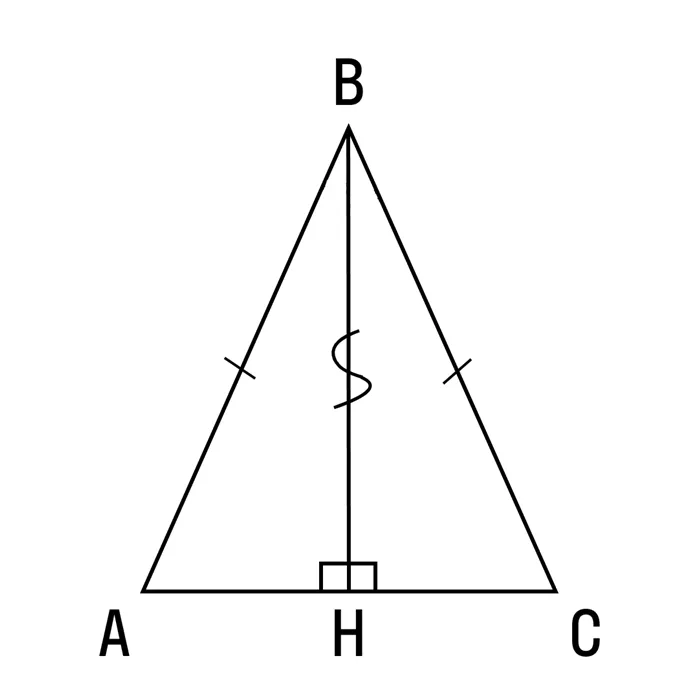
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Принцип прямоугольного треугольника ΔABH=ΔCBH, равенство субъекта и соответствующего перпендикуляра (bh — общая сторона, так как ab = bc равнобедренный).
Таким образом, во-первых, углы ABH и CBH равны, а BH является биссектрисой.
Во-вторых, AH = HC и BH — медианы.
Примеры решения задач
Нет ничего более приятного, чем практиковаться и искать углы и стороны в равнобедренном треугольнике. Ну… Почти ничего.
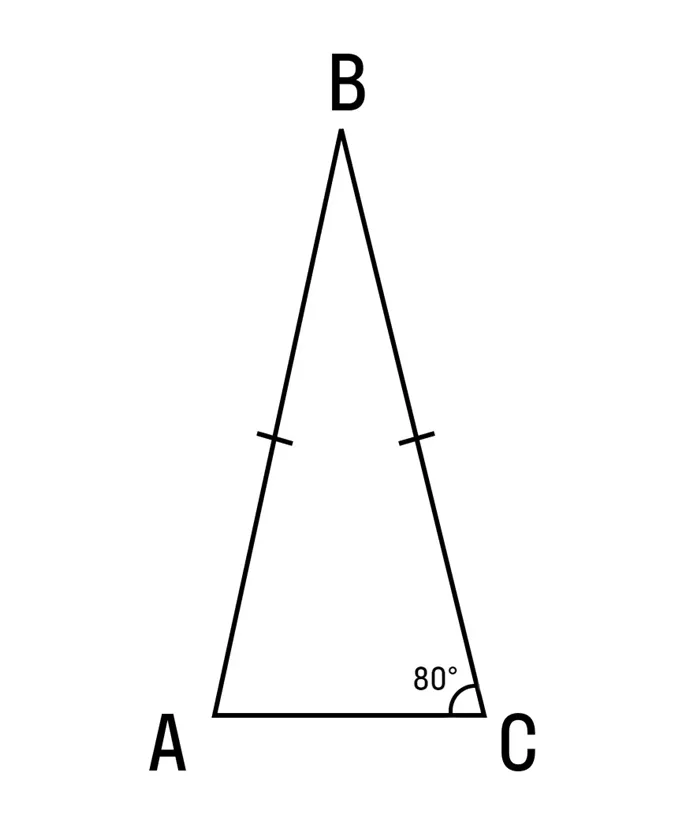
Первая проблема. Дано ΔABC на основе AC: ∠C = 80°, AB = BC. Найдите Notb.
Поскольку вы уже знакомы с различными теоремами, не секрет, что углы при основаниях равнобедренных треугольников равны и что треугольник ABC является равнобедренным, так как ab = bc.
Вас также не должен удивлять тот факт, что сумма углов треугольников равна 180°.
Проблема номер два. Найдите высоту BH в треугольнике ABC, угол cab равен 50°, а угол HBC равен 40°. Для BA = 5 см найдите сторону BC.
Сумма углов треугольника равна 180°, поэтому при δABH угол ABH равен 180° — 50° — 90° = 40°.
Затем находим, что углы ABH и HBC равны 40°, а BH является биссектрисой.
Так как BH — биссектриса высоты, d ABC — равнобедренная, поэтому BC = BA = 5 см.
Лучший способ найти качество и точки равновесного треугольника — это урок математики с опытным преподавателем Skysmart.
Равнобедренный треугольник — это треугольник, у которого обе стороны равной длины (называются сторонами). Оставшаяся часть третьей стороны является основой формы.
Равнобедренный треугольник: определение, теорема о свойстве высоты
Равнобедренный треугольник — это треугольник с равными сторонами.
Равная сторона называется боковой, а третья сторона — основанием.
Признаки равнобедренного треугольника
- треугольник является равнобедренным, если два его угла равны;
- треугольник, в котором высота и медиана, высота и биссектриса, биссектриса и медиана, проведенные к одной стороне, совпадают, является равнобедренным, а эта сторона – основанием.
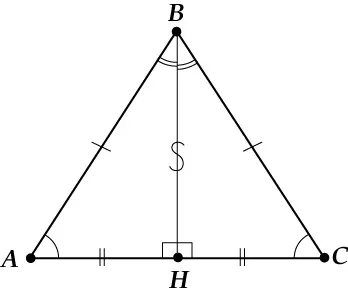
Свойства равнобедренного треугольника
Свойство первое
В равнобедренном треугольнике углы основания равны.
Внимание. Если преподаватель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до выкидыша). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Дана равнобедренная фигура DABC, где ab = ac. В ее основании находится дикатор ad.
Поскольку каждый AD является бисекторальным, угол ¶1 равен углу ρ2. Рекламная часть является общей для DADB и DADC. Поэтому она равна первой функции. Далее, угол ∠B равен углу amc.
Свойство второе
В равнобедренных треугольниках биссектрисы, падающие на основание, являются медианой и высотой.

Дана равнобедренная фигура DABC, где ab = ac. В ее основании находится дикатор ad.
Поскольку каждый AD является биссектрисой, угол ¶1 равен углу ρ2. Рекламная часть является общей для DADB и DADC. Тогда эти треугольники равны первому знаку. Тогда bd = dc. Следовательно, AD — медиана.
Сумма углов треугольников равна 180°, то есть am a + am b +∠C = 180°. Угол am a = 2*¶1, так как ad — биссектриса.
dACD∠CDA +∠1 +∠2= 180°, поэтому ¶cda = 90°.
Свойство третье
В изоширном треугольнике интерстиции, спроектированные вершиной основания (соответственно, высота и лучшая из них) равны.
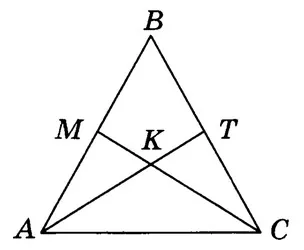
ab = ac.
Поскольку AT и MC — биссектрисы равных углов, ∠BAT = ∠BCM. ∠B является общим для ΔABT и ΔCBM. Поэтому ΔABT и ΔCBM равны со вторым знаком. Далее, AT=CM.
Мы узнали, что такое основания треугольника. Среди прочих аспектов треугольника мы обсудили, когда стоит акцентировать внимание на основании, а когда это оказывается пустой тратой времени. Мы обсудили важность основания треугольника изошеллы.
Доказательство равенства треугольников
Смотрите внимательно, у нас есть:.
- \( \displaystyle \underbrace_=\underbrace_\)
- \( \displaystyle BH\text< >= \ текст< >BH\) (ещё говорят, \( \displaystyle BH\)— общая)
так \ текст< >= \ текст< >(ch \)!
Да, по теореме Пифагора мы просто находим \ (\ displaystyle ah \) и \ (\ displaystyle ch \) (\ (\ displaystyle ab = bc \)).
Ты серьезно? Ладно, теперь у нас
Все три стороны являются простейшим (третьим) символом, указывающим на то, что треугольники равны.
Таким образом, равнобедренный треугольник делится на два одинаковых прямоугольных треугольника.
Обратите внимание, что все элементы изображения одинаковы (углы и стороны).

Видите, как это интересно? Это доказывает следующее
- В равнобедренном треугольнике углы при основании равны: \( \displaystyle \angle A=\angle C\);
- Высота, проведенная к основанию \( \displaystyle (ВH)\), совпадает с медианой и биссектрисой
- \( \displaystyle AH=CH\)
- \( \displaystyle \angle 1=\angle 2\).
(Помните, что здесь медиана — это линия, проведенная из вершины и делящая стороны пополам, а биссектриса делит угол).
Итак, мы обсудили, что можно увидеть, если взять равнобедренный треугольник.
Делаем вывод, что равнобедренные треугольники имеют равные углы при основании и что высоты, биссектрисы и медианы, проведенные к основанию, совпадают.
И теперь возникает другой вопрос: как узнать, является ли треугольник равнобедренным?
Другими словами, как говорят математики, что является точкой равнобедренного треугольника?
Признаки равнобедренного треугольника
Тогда получается, что нужно перевернуть все утверждения с ног на голову. Конечно, это не всегда так, но равнобедренный треугольник — это все равно здорово! Что же мы получаем после «перевертывания»?
Если у треугольника два равных угла, то это равнобедренный треугольник (разумеется, эти углы находятся при основании).
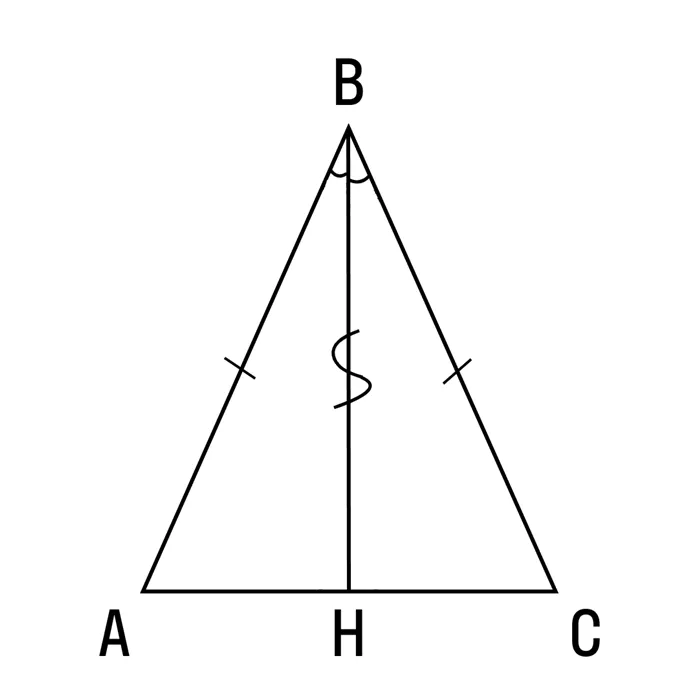
Если высота и медиана, или высота и биссектриса, или биссектриса и медиана, проходящие через одну сторону треугольника, совпадают, то этот треугольник — равнобедренный, а эта сторона — основание.
Смотрите: если высота и медиана совпадают, то
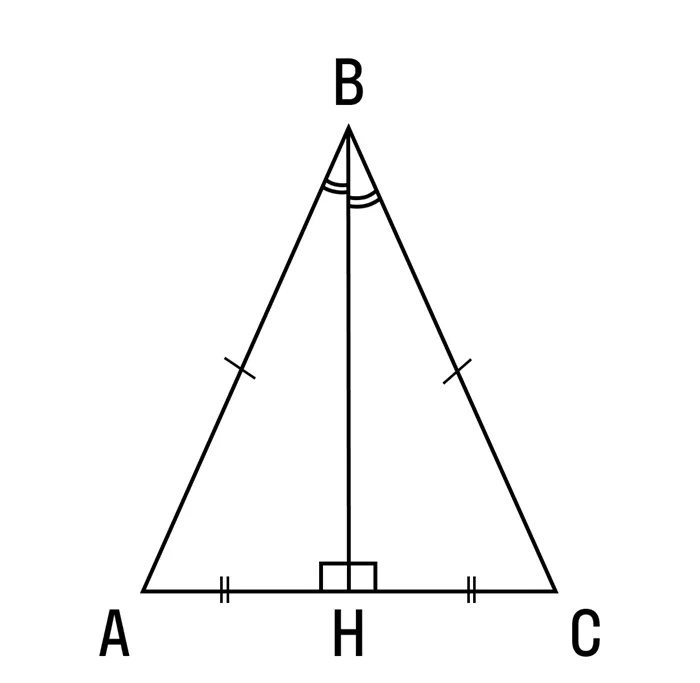
Если высота и биссектриса совпадают, то
Если биссектриса и медиана совпадают, то
Вот, запомните это и используйте:.
Как пользоваться признаками равнобедренного треугольника при решении задач
- Если дан равнобедренный треугольный треугольник, смело проводи высоту, получай два прямоугольных треугольника и решай задачу уже про прямоугольный треугольник;
- Если дано, что два угла равны, то треугольник точно равнобедренный и можно проводить высоту и ….( Дом, который построил Джек… 🙂 );
- Если оказалось, что высота разделила сторону пополам, то треугольник – равнобедренный со всеми вытекающими бонусами;
- Если оказалось, что высота разделила угол полам – тоже равнобедренный;
- Если биссектриса разделила сторону пополам или медиана разделила угол, то это тоже бывает только в равнобедренном треугольнике.
Давайте посмотрим, как это проблематично.
Поскольку каждый AD является бисекторальным, угол ¶1 равен углу ρ2. Рекламная часть является общей для DADB и DADC. Поэтому она равна первой функции. Далее, угол ∠B равен углу amc.
Видео
Ниже приведено простое правило, облегчающее определение того, является ли равнобедренный треугольник равнобедренным.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!
Равнобедренный треугольник
Равнобедренные треугольники — единственный вариант треугольника, в котором основание действительно значимо. Равнобедренный треугольник — это треугольник с двумя сторонами, равными друг другу. Равные стороны называются боковыми сторонами, а третья сторона — основанием.
Существуют две теоремы для основания равнобедренного треугольника. К ним относятся.
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.
В равнобедренном треугольнике основание определяется величиной боковых сторон. Равная сторона — это ребро, а неравная сторона — основание.
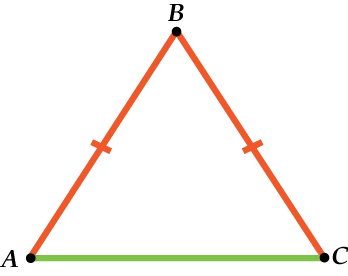
Рисунок 2. Равнобедренный треугольник.
В процессе решения задачи основание может оказаться поперечным. Не пугайтесь этого, так как основание может быть признано горизонтальным. Стоит привыкнуть к такому построению равнобедренных треугольников или каждый раз переделывать узор, направляя треугольники в нужную сторону.
Что мы узнали?
Мы узнали, что такое основания треугольника. Среди прочих аспектов треугольника мы обсудили, когда стоит акцентировать внимание на основании, а когда это оказывается пустой тратой времени. Мы обсудили важность основания треугольника изошеллы.
Математические объемы прямоугольников — виды вычислений
Свойства математического сложения — примеры (5 класс, Математика)








