В радиусно-угловой системе единицей измерения является острый угол ($ MON $), а из центра окружности выходит дуга длиной $MN$, равной радиусу ($ mathop Limits ^ = OM $). Этот угол называется радиусом.
Формулы перехода от синуса к косинусу
Виды синуса, косинуса, тангенса и диагонали угла следующие
sin(-α)=-sinαcos(-α)=cosαtg(-α)=—tgαctg(-α)=—ctgα
Сокращения всех типов можно получить, используя следующие правила: 1. Правая часть типа должна иметь тот же знак, что и левая часть.
2. если в левой части уравнения угол равен /2± или 3/2±, то синус заменяется диагональным тангенсом, косинус, если угол равен ± или 2k. Происходит замещение.
Уравнение перехода от суммы к продукту.
Уравнение перехода от продукта к сумме.
Тип для снижения класса.
Введите вспомогательные аргументы для преобразования выражения a-cos+b-sin.
Где вспомогательные аргументы определяются ситуацией.
Основные тригонометрические типы — это выражения, которые определяют отношения между основными тригонометрическими функциями. Синус, косинус, тангенс и тангенс взаимосвязаны. Ниже приведены основные тригонометрические формулы, сгруппированные для удобства по назначению. Эти формулы можно использовать для решения практически любой задачи в стандартном курсе тригонометрии. Обратите внимание, что ниже приведены только сами формулы, а не их выводы. Они будут применяться к отдельным статьям.
Основные тождества тригонометрии
Тригонометрические тождества соотносят синус, косинус, тангенс и четырехугольник угла таким образом, что одна функция может быть выражена в терминах другой.
sin2α+cos2α=1tgα=sinαcosα, ctgα=cosαsinαtgα—ctgα=1tg2α+1= 1cos2α, ctg2α+1= 1 sin 2 a
Эти тождества вытекают непосредственно из определений единичного цикла, синуса (sin), косинуса (cos), тангенса (tg) и когната (ctg).
Формулы приведения
Используя тип редукции, вы можете перейти от работы с любым произвольно большим углом к работе с углами от 0 до 90 градусов.
sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=—ctgαsinπ2+α+2πz=cosα, cos cos π2+ α+2πz=—sinαtgπ2+α+2πz=—ctgα, ctgπ2+α+2πz=—tgαsinπ2-α+2πz=cosα, cos π2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=-tgαsinπ+α+2πz=- sinα, cos π+α+2πz=—cosαtgπ+α+2πz=-tgα, ctgπ+α+2πz=-ctgαsinπ-α+2πz=-sinα, cosπ—α+2πz=—cosαtgπ—α+2πz=-tgα, ctgπ—α+2πz=—ctgαsin3π2+α+ 2πz = —cosα, cos 3 π2+α+2πz = sinαtg3π2+α+2πz = -ctgα, ctg3π2+α+2πz = —tgαsin3π2-α+2πz = —cosα, cos3π2-α+2πz = —sinαtg3π2-α+2πz = c tgα, ctg3π2-α+2π z=tgα
Типы уменьшения являются результатом периодичности тригонометрических функций.
Для удаления отрицательных угловых измерений при вычислении синуса, косинуса или тангенса можно использовать следующее тригонометрическое преобразование (ID), основанное на принципе избыточности или тригонометрической избыточности.
Определения основных функций
Первоначально понятие тригонометрических функций, значением которых является угол, вычислялось по соотношению сторон треугольника с прямыми углами.
Определение острого угла прямоугольника.
- Функция Sin a — Синус угла — отношение напротив лежащего катета к гипотенузе
- Cos a — Косинус угла — отношение стороны треугольника (катета), который прилегает к данному углу и гипотенузы;
- Tg a — Тангенс угла — отношение стороны треугольника который называется катетом и лежит напротив угла к прилежащему углу катету ;
- Ctg a — Котангенс угла — прилежащего катета к противолежащему.
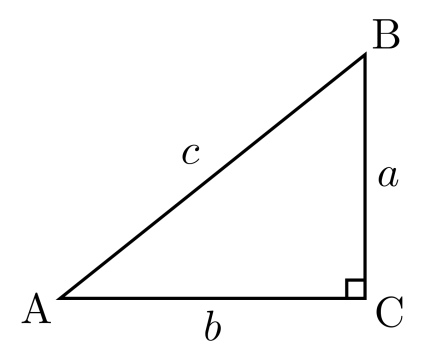
Теорема синусов в формуле:
Определение, которое мы рассмотрели выше, относится к острому углу треугольника. Однако существует также понятие угла поворота. В этом случае вычисленный угол не может быть значением от 0 до 90 градусов. Угол поворота может быть любым числом между + бесконечность и — бесконечность.
В этом контексте можно дать определения синуса, косинуса, тангенса и диагонали углов любого размера. Для этого представим окружность в системе координат, где две оси перпендикулярны друг другу.
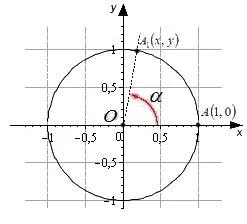
Особая точка A с координатой 1.0 вращается вокруг центра оси на угол α и проходит через точку A1.
Синус угла α является прямым углом точки A1 (x, y). Это означает, что sinα= u
Синус α — это отклонение точки A1 (cosα= x).
Tg-‘ данного угла — это деление (отношение) A1 к прямому дистальному углу. tgα= y\ x
Угол поворота вертлужной впадины α — это отношение края к его ординате, ctgα= x \ u
Обратите внимание, что полутоны и косинусы можно различить под любым углом, а касательные и диагонали — нет. И это вполне логично. Это связано с тем, что если точка имеет нулевую координату по оси абсцисс, то ее нельзя разделить на ноль и, следовательно, нельзя вычислить линию касательной. То же самое справедливо и для значений вертикальной координаты, равных нулю. Рассчитано.
Синус и кос можно вычислить для любого угла a. α=90°+180°*k, k∈Z (α=π2+ π* k, k∈Z)
Четырехугольники также не могут быть вычислены для всех углов. Этого нельзя сделать для α=180°*k, k∈Z (α=π* k, k∈Z).
Обратите внимание, что на практике, при решении примера, угол поворота фразы опускается из речи.
Для удобства имеется таблица, содержащая значения часто используемых углов, вычисляемых с помощью тригонометрических функций. Например, для первой четверти окружности таблица выглядит следующим образом
| 0° | 30° | 45° | 60° | 90° | |
| sin | 0 | 1 2 | √2 2 | √3 2 | 1 |
| cos | 1 | √3 2 | √2 2 | 1 2 | 0 |
| tg | 0 | 1 √3 | 1 | √3 | – |
| ctg | – | √3 | 1 | 1 √3 | 0 |
Здесь можно посмотреть таблицу синусов, косинусов и других функций.
Вычисление тригонометрических функций числа
В этом разделе мы рассмотрим случаи, когда рассматриваемые тригонометрические определения выводятся из числовых значений, а не из углов. Существует два таких подхода.
- Sin, cos, tg, ctg числа n, является число которое равно sin, сos, tg, ctg n радиан. Где Радиа́н это угол, который соответствует дуге, которая в свою очередь равна длине, её радиуса. Пример: sin числа2k=sin угла2k радиан. Используя формулы можно получить таблицу часто встречаемых углов, которая поможет быстро перевести значения из градусов в радианы и в противоположную сторону.
- На прямоугольной системе координат, в единичной окружности, ставится точка, которой соответствует любое действительное значение числа d. тригонометрические функции можно определить, узнав координаты этой точки.
- Считая начальной точкой А с координатами (1,0). Поэтому для того чтобы найти взаимодействие между точкой на окружности и числом, нужно найти отрицательное и положительное значение числа d, положительным будет значение при движении точки А(1,0) в противоположную сторону движения часовой стрелки и её движение будет равным open t \ t, а отрицательным движение по часовой стрелке.
С этой точки зрения можно выделить следующие функции.
- (sin f = y) Синус числа f- определяется ординатой точки единичной окружности, которая равна числу f;
- (cos f = x) Косинус числа f — абсцисса окружности, которая соответствующая числу f;
- (tg f = y\x=sin f\cos f) тангенс f определяется делением ординаты на абсциссу точки, равной числу f.
Далее перейдем непосредственно к самим формулам. Эти типы соединяют синус, косинус, тангенс и четырехугольник угла. Каждый из них является результатом конкретного определения.
Решение уравнения cos x = a
| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | В случае, когда, уравнение решений не имеет |
Формат записи обычного решения:.
Более удобная форма для записи решений:
уравнение не имеет решения.
Графическое представление решения уравнения cosx=a показано на рисунке 2.
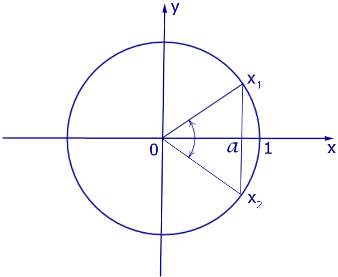
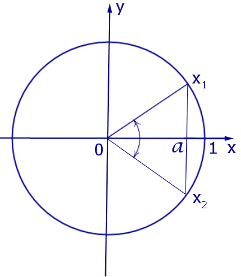
Некоторые случаи решения уравнения cosx=a
Это соотношение помогает быстро решить уравнение sin x=1, легко запомнив значение x, для которого синус равен единице.
Некоторые хроматические случаи лучше всего видны в единичном круге, как и некоторые косинусные случаи.
Таким образом, косинусы являются колобусами. Оба начинаются с co, а буква o, названная cosx, кажется круглой колонной.
Как движется колобок? Он не может отскакивать влево, вправо, по кругу, вверх или вниз. На уровне координат x перемещается влево и вправо. Таким образом, косинус равен x, а синус равен y.
Поэтому, чтобы найти, где sin x = 1, нужно найти, где в единичном круге y = 1. Двигайтесь вверх по оси y и дойдите до точки p/2.
Это лишь одна из точек, где sin равен 1.
Достигните этой точки снова через 2, 3 и т.д., после того как круг полностью повернется. Вращение.
Двигаясь по часовой стрелке, т.е. -2p, -2p-2, -2p-3 и т.д., эта точка также достигается.
Чтобы учесть все точки, где sin x = 1, прибавьте 2n к n / 2. где n — целое число (n принадлежит Z). То есть, n = 0, ±1, ±2, ±3, …
Метафора для синуса и косинуса: купол
Помимо рассмотрения самого треугольника, найдите личный пример из своей жизни и представьте реальный треугольник.
Представьте, что вы находитесь в центре купола и хотите повесить экран для проектора. Направьте палец на навес под углом «x», и экран зависнет в этой точке.
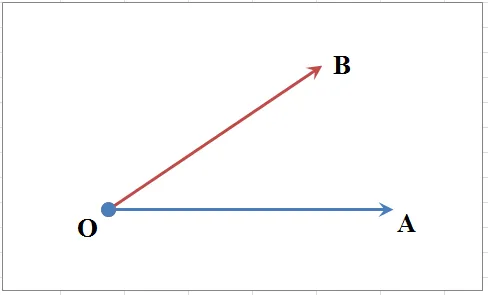
Угол, под которым вы наводите курсор, определяет:.
- синус(x) = sin(x) = высота экрана (от пола до точки крепления на куполе)
- косинус(x) = cos(x) = расстояние от вас до экрана (по полу)
- гипотенуза, расстояние от вас к верхушке экрана, всегда одинаковое, равно радиусу купола
Вы хотите, чтобы экран был как можно больше? Повесьте его прямо над собой.
Вы хотите, чтобы экран висел как можно дальше? Повесьте его точно вертикально. В этом положении высота экрана равна нулю, а дальше он откидывается по желанию.
Высота экрана и расстояние до него обратно пропорциональны. Чем дальше висит экран, тем больше высота экрана.
Предположим также, что определения синуса, косинуса, тангенса и пятиугольника острого угла прямоугольного треугольника соответствуют определениям синуса, косинуса, тангенса и четырехугольника угла от 0 до 90 градусов. Это обосновано в последнем абзаце данного документа.
Числа
Как насчет определений синуса, косинуса, тангенса и когональных чисел вместо угла поворота?
Полутон, косинус, тангенс и квадрат числа
Синус, косинус, тангенс и косинус числа t — это числа, равные соответственно синусу, косинусу, тангенсу и четырехугольнику прямой t.
Например, синус числа 10π равен синусу угла поворота радиуса 10π.
Существуют альтернативные подходы к определению синуса, косинуса, тангенса и котангенса числа. Давайте посмотрим на детали.
Каждое вещественное число t соответствует точке на единичной окружности с центром в начальной точке декартовой системы координат. Синус, косинус, тангенс и четырехугольник определяются координатами этой точки.
Начальной точкой окружности является точка A с координатами (1, 0).
Положительное число t соответствует точке, в которую перемещается начальная точка, если начальная точка движется против часовой стрелки по окружности и перемещается по пути t.
Отрицательное число t соответствует точке, в которую перемещается начальная точка, если начальная точка движется против часовой стрелки по кругу и проходит расстояние t.
Определив связь между числами и точками на окружности, мы можем перейти к определениям синуса, косинуса, тангенса и кита.
Синус числа t — это линия точек на единичной окружности, соответствующих числу t. sin t = y
Синус числа t — это отклонение точек единичной окружности, соответствующих числу t. cos t = x
Тангенс числа t — это отношение точки единичной окружности, соответствующей числу t, к пропасти. t g t = y x = sin t cos t
Последнее определение совпадает и не противоречит определению, данному в начале этого параграфа. Точка окружности, соответствующая числу t, совпадает с точкой, в которую перемещается начальная точка после ее поворота на угол радиусом t.
Тригонометрические функции углового и числового аргумента
Каждому углу α соответствует определенное значение синуса и косинуса этого угла. Как и всем углам α, кроме α=90°+180°—k, k∈Z (α=π2+π—k, k∈Z) соответствует определенное значение линии касания. Как упоминалось выше, котенант определен для всех α, кроме α = 180°—k, k ∈ Z (α = π—k, k ∈ Z).
Можно сказать, что sinα, cosα, tgα и ctgα являются функциями углов альфа или угловыми терминами.
Подробнее: рассчитать вероятность выигрыша. Каковы ваши шансы выиграть в лотерею? Это удача или математический расчет? Статистика выигрышей в лотерею
Аналогично можно говорить о синусе, косинусе, тангенсе и цыпленке как о функции числовых выражений. Каждое действительное число t соответствует определенному значению синуса или количеству чисел. Каждое число, кроме π2 +π -k, k ∈ Z, имеет значение тангенса. Аналогично, котензиоген определен для всех чисел, кроме π -k, k ∈ Z.
Основными функциями тригонометрии являются.
Синус, косинус, тангенс и цыпленок — основные тригонометрические функции.
Обычно из контекста понятно, в каком контексте мы имеем дело с тригонометрическими аргументами (угловыми или числовыми).
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Давайте вернемся к первому приведенному определению и вернемся к углам альфа от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса прекрасно согласуются с геометрическим определением, которое дается пропорциями прямоугольного треугольника. Давайте покажем это.
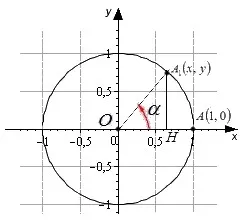
Возьмем единичную окружность с центром в прямоугольной системе координат Декарта. Поверните начальную точку A (1, 0) на угол до 90 градусов и установите вертикальный перпендикуляр из этой точки. В прямоугольном треугольнике угол a 1 o h равен углу поворота A, а длина катетера o h равна дальнему положению точки a 1 (x, y). Длина перпендикуляра, противолежащего углу, равна прямому углу в точке a 1 (x, y), а длина предмета равна единице. Это связано с радиусом единичной окружности.
Согласно определению геометрии, половина угла a равна слову, противоположному гипотенузе.
sinα= a 1 h o a 1 = y 1 = y
Таким образом, определение синуса острого угла прямоугольного треугольника через боковой голос эквивалентно определению угла A с альфой между 0 и 90 градусами.
Аналогичные соответствия определения можно доказать для косинуса, тангенса и конъюгаты.
Хорошие и плохие случаи поясняют, что подчиненной является сторона треугольника, прилегающая к углу 90 градусов, а две другие стороны называются прямоугольными треугольными катетами.
Формулы двойного угла
Тип «двойной угол» соотносит тригонометрические функции угла (синус, косинус, тангенс и цыпленок) с тригонометрическими функциями угла.
Первое тождество получается в результате добавления дополнительного вида синуса, после чего добавляется аналогичная сумма. Вторая идентичность аналогична. Что касается двух последних тождеств (3 и 4), то каждое из них вытекает из типа.
Формулы половинного угла
Вид угловых половин задается тригонометрическим квадратом.
Первые два типа (синус и косинус) применимы к любому углу. Третий тип (Tangent) применяется к каждому углу. И четвертый, тип Half Angle Cochilian, применяется ко всем углам альфы, при этом определяется Half Angle Cochilian (Half Angle Cochilian).
Формулы понижения степени
Тип понижения степени — собственно тригонометрический, который позволяет перейти от тригонометрической степени к первой функции. Однако, исходя из многочисленных аргументов.
Типы суммы и разности облегчают упрощение тригонометрических уравнений. Они также часто используются для решения тригонометрических уравнений. Рассмотрим типы суммы и разности.
Тип понижения степени — собственно тригонометрический, который позволяет перейти от тригонометрической степени к первой функции. Однако, исходя из многочисленных аргументов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, имеющие вид sin sum A + sin b, можно преобразовать с помощью следующих типов.
Иногда необходимо преобразовать тройной угол так, чтобы аргументом тригонометрической функции был угол A, а не 3a. В этом случае можно использовать тип тройного преобразования (ID).
Формулы преобразования произведения тригонометрических функций
Если вам нужно преобразовать синусоиды различных углов в косинусы различных углов или синусы в косинусы, вы можете использовать следующие тригонометрические тождества.
В этом случае произведение синуса, конгруэнты или тангенса разных углов превращается в сумму или разность.








