Для закрепления теоретического материала преподаватель просит студентов решить ряд задач. Преподаватель предоставляет студентам серию задач для закрепления теоретического материала. Такие задачи предназначены для учащихся средней школы.
Виды треугольников по углам
Треугольники расположены в соответствии с их углами: кислородный — тупоугольный — прямоугольный.
| Остроугольные | Тупоугольные | Прямоугольные |
| Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС. | Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой. | Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0. Такой угол в любом прямоугольном треугольнике – единственный. |
 |
 |
 |
Виды треугольников по сторонам
Треугольники расположены в соответствии с их сторонами: односторонний — равнобедренный — равнобедренный треугольник.
| Разносторонний | Равнобедренный | Равносторонний |
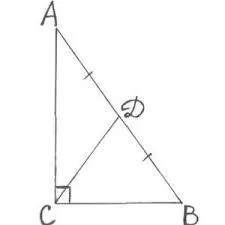
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
 |
 |
Медиана, биссектриса, высота, средняя линия треугольника
Часть треугольника, соединяющая вершину и центр противоположной стороны, называется центром треугольника.
Поскольку сторон три, для любого треугольника можно построить три медианы. На этой диаграмме показаны медианы (AF, EC и BD) треугольника ABC.

Это также показывает, что медианы пересекаются в точке O. Это справедливо для всех треугольников.
Прямоугольные треугольники — это треугольники с углом 90°, если кто-то забыл об этом. И в такой форме медиана обладает уникальными свойствами.
Определение и свойства медианы треугольника
В этой статье рассматривается определение треугольника и перечисляются его свойства. В нем также рассматриваются примеры задач для закрепления теоретического материала.
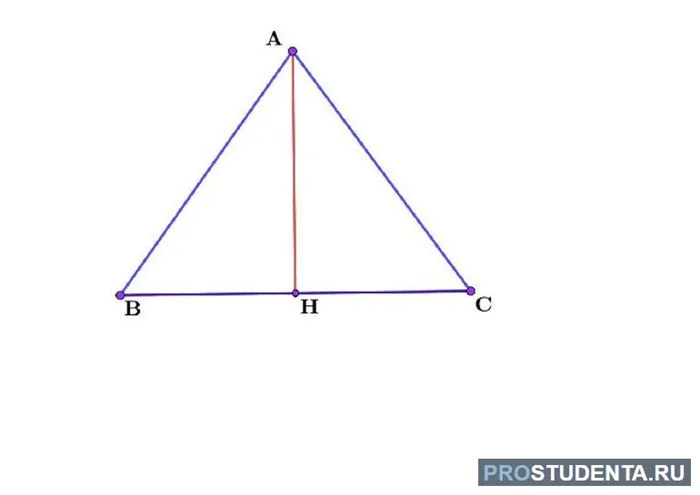
Медиана — это часть треугольника, соединяющая вершину с центром стороны, противоположной этой вершине.
Основанием медианы является точка пересечения медианы и одной из сторон треугольника, центр этой стороны (точка F).
Свойства медианы
Свойство 1 (основное)
Поскольку треугольник имеет три вершины и три стороны, в нем есть три медианы. Все они пересекаются в одной точке (O). Это называется центром тяжести или центром масс треугольника.
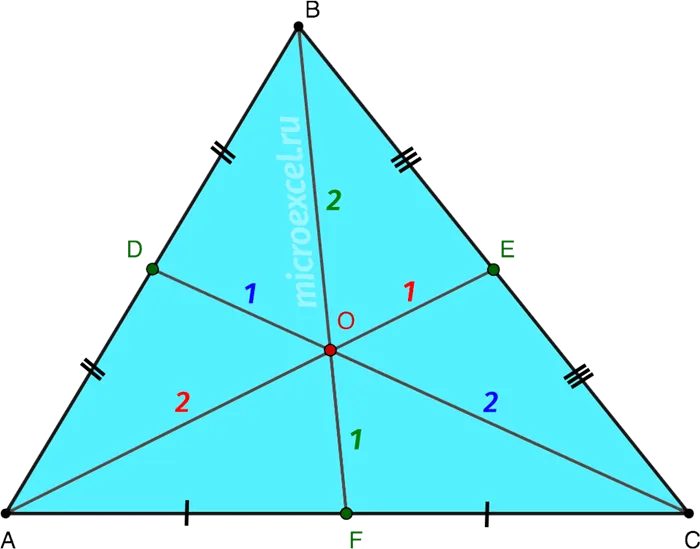
При пересечении перпендикулярных линий каждая из них отсчитывается сверху и делится на 2:1. То есть:.
Свойство 2
Медиана делит треугольник на два равных (одинаковой площади) треугольника.
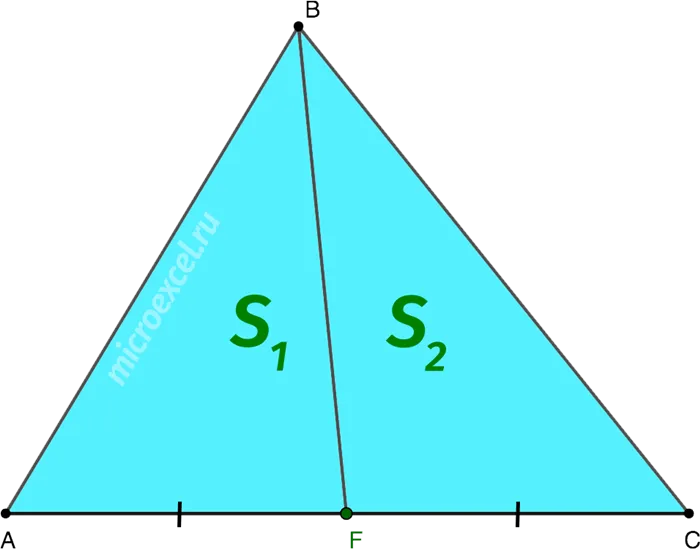
Свойство 3
Три медианы делят треугольник на шесть равных треугольников.
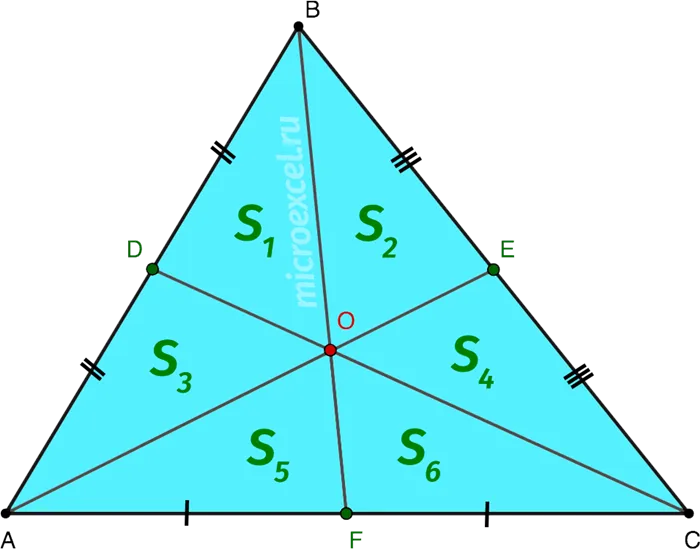
Свойство 4
Наименьшая медиана соответствует наибольшей стороне треугольника и наоборот.
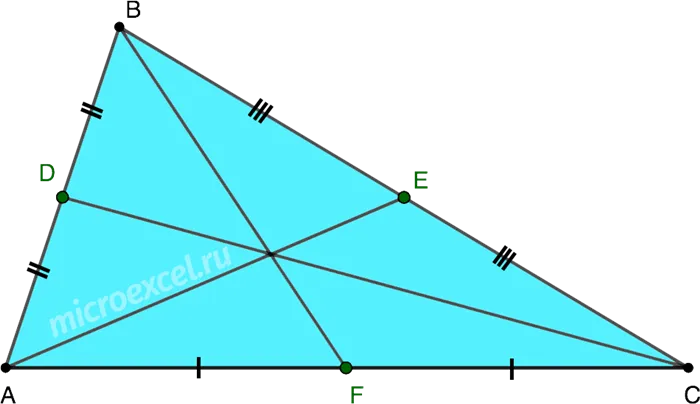
- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
Предположим, что все стороны треугольника известны (a, b, c).
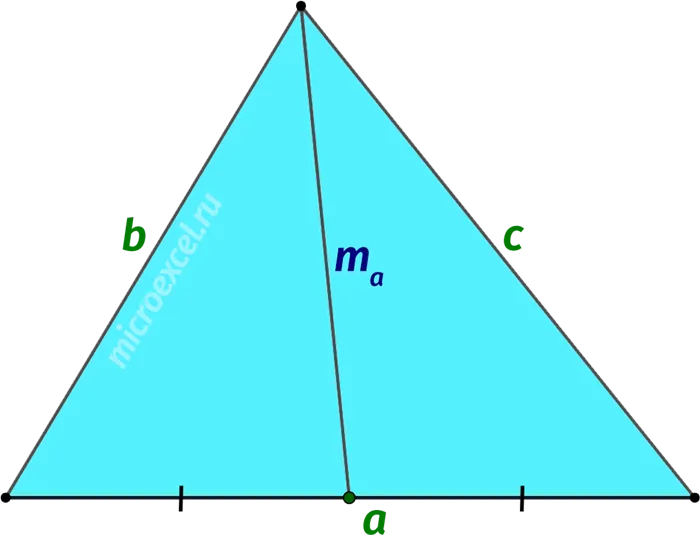
Длина медианы ma заданный уравнением, можно найти из следующего уравнения.
Примеры задач
Площадь одной из фигур, образованных пересечениями трех перпендикулярных линий треугольника из задачи 1, равна 5 см2. Найдите площадь треугольника.
Решение В соответствии со свойством 3 выше, в результате пересечения трех перпендикулярных линий получается шесть треугольников равной площади. Поэтому: s△ = 5 см2 и 6 = 30 см2.
Задача 2: Стороны треугольника равны 6, 8 и 10 см. Найдите середину стороны длиной 6 см.
Однако урок по этой теме показывает, что это действительно так. Это правда, что сложные проблемы редко решаются одной теоремой — почти всегда они разбиваются на несколько более мелких проблем.
Медиана треугольника.

Медиана и высота треугольника выступают в качестве графических параметров, определяющих величину всего треугольника, его сторон и углов. Три значения — медиана, высота и биссектриса — подобны штрих-коду продукта. Наша задача — уметь их измерять.

Определение
Медиана — это соединение между высотой и серединой на другой стороне. Поскольку треугольник имеет три вершины, медиана равна трем. Медиана не обязательно совпадает с высотой или биссектрисой. В большинстве случаев это отдельные разделы.
- Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
- Все медианы треугольника пересекаются в одной точке.
- Медиана делит треугольник на два равновеликих, а три медианы, на 6 равновеликих треугольников.
- Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Задачи
Все эти качества легко запомнить и практиковать. Чтобы лучше понять проблему, давайте разберемся в некоторых вопросах.
- В прямоугольном треугольнике известны катеты, которые равны a=3 и b=4. Найти значение медианы m, проведенной к гипотенузе c.
Чтобы найти цену через, нужно найти подчиненные, потому что нижняя медиана равна половине. Найдите подчиненные по теореме Пифагора: $ a^2+b^2 = c^2 $
Найдите значение $ m =.
Цены на треугольные интерстиции не равны. Поэтому очень важно понять, какие ценности необходимо найти.
- В треугольнике известны значения сторон : a=8; b=7; c=9. Найти значение медианы, опущенной к стороне b.

Рисунок 3.Изображение проблемы.
Чтобы решить эту задачу, нужно найти стороны треугольника, используя один из трех типов.
Как видите, главное здесь — запомнить факторы брекзита и знаки боковых цен. Знаки легче всего запомнить — всегда убирайте ту сторону, где падает медианная цена. В данном случае она одна, но могут быть и другие стороны.
Замените значения пресса и найдите значение $ m = \ sqrt<<1\over2>*(b^2+c^2-a^2)> $
$ m = \ sqrt<<1\over2>*(49+81-64)> = \ sqrt $ — корень из результата.
- В равнобедренном треугольнике медиана, проведенная к основанию равна 8, а само основание – 6. Вместе с оставшимися двумя, эта медиана делит треугольник на 6 треугольников. Найти площадь каждого из них.
Посредник делит треугольник на шесть равносторонних треугольников. Поэтому площади меньших треугольников равны между собой. Достаточно найти наибольшую площадь и разделить ее на 6.
Учитывая медиану, проведенную к основанию, равнобедренные треугольники являются биссектрисой и высотой. Таким образом, основание и высота треугольника известны. Поиск района.
Площадь каждого из меньших треугольников: $<24\over6>= 4 $
Однако на практике исходные данные, используемые для нахождения через, могут представлять собой радикальные, динамические и дробные выражения и поэтому требуют выполнения длительных и сложных вычислений. Существует риск совершения ошибок, которые могут привести к неправильным ответам.
Как найти медиана треугольника
Термин «медиана» переводится как «на равной стороне». Для построения медианы центр одной стороны треугольника должен быть соединен с противоположной стороной треугольника. Полученное сечение представляет собой медиану треугольника.
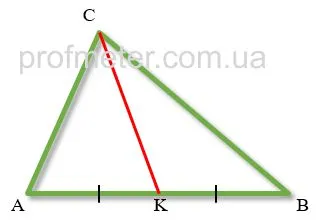
Медиана треугольника. — Это отрезок, вписанный в вершину треугольника и соединяющий эту вершину с медианой центра противоположной стороны треугольника.
Интерстициальный CK показан красным цветом. Сторона AB центрального треугольника делится AK = KB.
Свойства медианы треугольника
Все они пересекаются друг с другом в общей точке на уровне треугольника.Центр тяжести. .
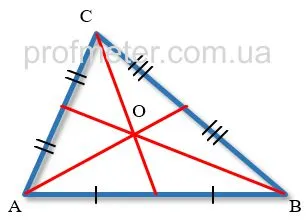
Для определения этой точки достаточно построить две медианы треугольника, а точкой пересечения будет третья медиана треугольника.
Используя пересечение промежуточных треугольников, каждая медиана измеряется от вершины треугольника и делится на 2:1. То есть длина средней части от вершины треугольника до пересечения с межвершинным расстоянием равна 2/3 его длины, а длина от пересечения межвершинного расстояния до стороны треугольника равна 1/3 его длины.
Медиана делит треугольник на два равных (по площади) треугольника.
Треугольник разделен на шесть равных треугольников с тремя медианными дисками.
Из отрезков, образующих медиану, можно построить треугольник, площадь которого равна 3/4 площади всего треугольника. Длина медианы удовлетворяет неравенству треугольника.
В прямоугольном треугольнике медиана, полученная из вершин прямых углов, равна половине предметов.
Большая сторона треугольника соответствует наименьшей медиане.
В равнобедренных треугольниках биссектрисы и высоты медиан, проведенных к основанию треугольника, совпадают.
В правильном женском треугольнике три «примечательные» линии (высота, дихотомос и медиана) совпадают, а три «примечательные» точки (ортографическая точка, центр тяжести и эндоциклический центр и периферия) находятся в «примечательных» местах.
Средняя линия треугольника
Сечение, проходящее через два основания среднего треугольника, является центральным классом треугольника.
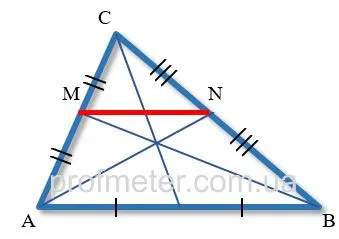
Средняя линия треугольника всегда параллельна сторонам треугольника, где нет общей точки. Средняя линия треугольника равна половине длины стороны треугольника, к которой она параллельна.
Медиана — это соединение между высотой и серединой на другой стороне. Поскольку треугольник имеет три вершины, медиана равна трем. Медиана не обязательно совпадает с высотой или биссектрисой. В большинстве случаев это отдельные разделы.
Теорема о трех медианах треугольника
Три точки пересечения треугольника пересекаются в некоторой точке, от этой точки они делятся на ዄ (ዄ displaystyle 2:1 \) и измеряются сверху.
Что это значит? Рисунок. На самом деле, в этой теореме есть два утверждения. Вы заметили это?
1. медианы треугольников пересекаются в одной точке.
2. точка пересечения делит интерстиций на \ (\ displaystyle 2:1 \) и измеряется сверху.
Поясним секрет этой теоремы, т.е. докажем ее.
Доказательство теоремы о трех медианах треугольника
Сначала спроектируйте только две медианы, а не все три. Они определенно пересекаются, не так ли? \Показать их пересечение с \(⌘ displaystyle e \).
Соединим точки ⌘ (⌘ displaystyle n \) и ߡ (ߡ displaystyle k \). Что у нас есть.
Конечно, ⌘ (⌘ displaystyle nk \) — это средняя линия ߡ (ߡ displaystyle \ треугольника abc \). Помните, что это значит?
Далее построим еще одну среднюю линию: отметим талию {{displaystyle ae \) — поставьте точку Ǿ (⌘ displaystyle f \) и отметим середину Ǿ (⌘ displaystyle ec \) — поставьте точку Ǿ (⌘ displaystyle g \). .
Теперь \ (⌘ displaystyle fg \) — средняя линия \ (⌘ displaystyle \ треугольник aec \). Среднее:.
Вы смотрели матч? И NK, и FG параллельны AC. и ዄ (ዄ displaystyle nk = ዄ frac \) и ዄ (ዄ displaystyle fg = ዄ frac \).
Далее рассмотрим четырехугольник ɑ (ɑ displaystyle nkgf \). Существуют ли параллельные и равные противоположности (⌘ (⌘ displaystyle nk) и 섹 (⌘ displaystyle fg \))?
Конечно, только в прямоугольниках!
Поэтому ɛ (ɛ displaystyle nkgf \) — это прямоугольник. Так что
Теперь давайте вспомним свойства прямоугольника. Например, что вы знаете о диагоналях прямоугольника? Он разделен с правым, центральным перекрестком.
Открыть ответы…
Мы постоянно совершенствуем этот семинар, и вы можете помочь в этом. Доступ и использование руководства «Юклава» без ограничений (все темы по использованию и применению, 2000+ решенных задач, 20+ онлайн-семинаров, 100+ статей по образовательным программам).
Мы постоянно совершенствуем этот семинар, и вы можете помочь в этом. Доступ и использование руководства «Юклава» без ограничений (все темы по использованию и применению, 2000+ решенных задач, 20+ онлайн-семинаров, 100+ статей по образовательным программам).
Треугольник
Рисунок 1. Треугольник (общий случай).
Так, треугольник, в котором длины всех сторон различны и ни один из углов не равен, называется произвольным (рис. 1).
- В случае, если у треугольника равны две стороны, данный треугольник называется равнобедренным .
- В случае, если у треугольника все стороны одинаковы, он называется равносторонним .
- В случае, если у треугольника один и углов прямой (), он называется прямоугольным .
- Для произвольного треугольника вводят ряд отрезков, характеризующих треугольник и обладающих собственными свойствами:
Для разных типов треугольников поиск параметров треугольника может осуществляться по-разному. Для естественных проблем использование того или иного типа определяется конкретными данными проблемы.
Рисунок 2.Треугольники (рассекающие полосы)
Биссектриса угла — это геометрическое положение знака, равного стороне этого угла. Другими словами, биссектриса — это линия, делящая угол центрального треугольника (рис. 2). Известно, что биссектрисы внутренних углов треугольника делят противоположную сторону на отрезки в соответствии с прилежащей стороной.
Для нахождения частей углов через различные данные можно использовать следующие соотношения
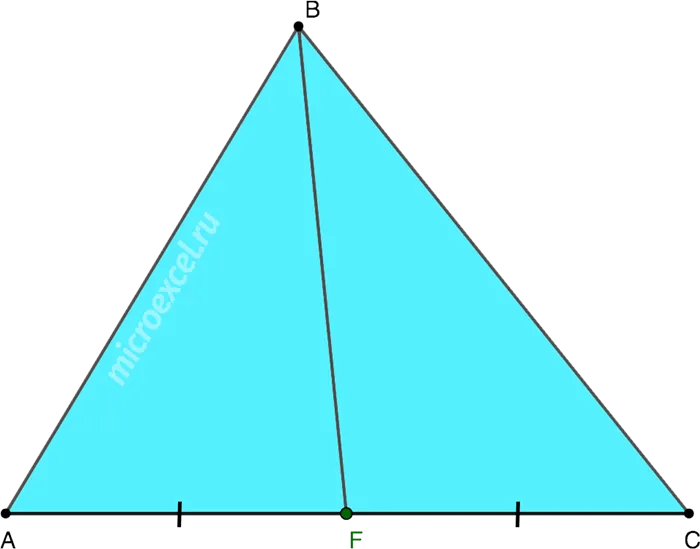
Медиана треугольника — это часть, соединяющая вершину треугольника с центром противоположной стороны. Все промежутки в треугольнике пересекаются в одной точке. Эта точка делит медиану в соотношении 2:1, измеряя от вершины (рис. 3).
Рис. 3. треугольник (медиана)
Для нахождения медианы треугольника по различным данным можно использовать следующие пропорции
Высота треугольника вертикальна, падает из вершины противоположного треугольника или его продолжения (рис. 4).
Вы можете найти высоту треугольника по различным данным, используя следующие пропорции
Важно: Тип, выбранный для решения конкретной задачи, зависит от того, что легче найти из данного








