Если отрезок перпендикулярен оси, то его проекцией является точка. В декартовых системах координат одно из положений вектора имеет нулевое значение. Например, AB (0; 1) или AB (-3; 0). Так называемые единичные векторы используются для определения направления в пространстве.
Формула длины отрезка в координатах. Нахождение координат середины отрезка, примеры, решения
Ниже приведен подробный пример определения длины отрезка при заданной координате с помощью онлайн-сервиса Контрольная работа Ru.
Предположим, вам нужно найти длину отрезка на плоскости
(В пространстве это можно вычислить по аналогии, изменяя только точки в трех измерениях).
Сегмент AB имеет концы A (1, 2) и B (3, 4).
Чтобы рассчитать длину отрезка AB, выполните следующие действия
1. перейдите на служебную страницу и найдите расстояние между двумя точками в интернете.
Это можно использовать, так как длина отрезка в координатах точно равна расстоянию между точками A и B.
Чтобы установить правильные размеры точки A, перетащите правый нижний край влево, как показано на рисунке.
После ввода координат первой точки A (1, 2) нажмите кнопку Точка A.
3. на втором этапе необходимо ввести координаты второй точки B, как показано на следующем рисунке.
Точки a и b введены! Решение:
Найдите расстояние между точками (s)
Отрезок — это сегмент прямой линии, состоящий из всех точек на линии между двумя определенными точками (называемыми краями отрезка).
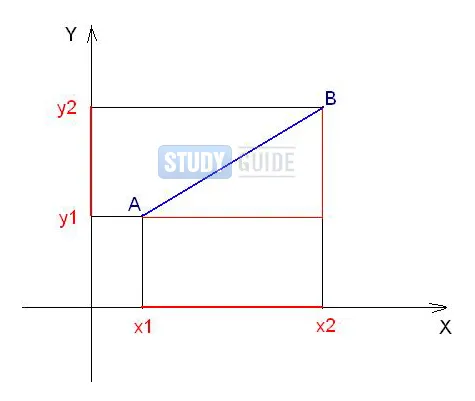
Рассмотрим первый пример. Пусть отрезок прямой задан двумя точками в координатной плоскости. Его длину можно найти, применив теорему Пифагора.
Таким образом, в системе координат отрезок рисуется путем указания координат ребер (x1; y1) и (x2; y2). Проведем от края отрезка перпендикулярно осям x и y. Отметьте красным цветом участок, который является проекцией исходного участка на координатные оси. Затем переместите проектируемый участок параллельно краю участка. (Получается треугольник (прямоугольный). Гипотенуза этого треугольника — отрезок АВ, а перенесенная проекция — его катет.
Вычислите длину этих видов. Таким образом, длина проекции на ось y равна y2-y1, а длина проекции на ось x равна x2-x1. Применим теорему Пифагора: || AB |²= (y2-y1)²+ (x2-x1)². В данном случае|AB| — это длина отрезка.
Если вы используете эту диаграмму для расчета длины отрезка, вам даже не нужно создавать этот отрезок. Затем рассчитывается длина отрезка с использованием координат (1; 3) и (2; 5). Применяя теорему Пифагора, получаем. | AB |²= (2-1)²+ (5-3)²= 1 + 4= 5. Это означает, что длина отрезка равна 5:1/2.
Чтобы найти длину отрезка, воспользуйтесь следующим методом. Для этого необходимо знать координаты двух точек в системе. Рассмотрим этот вариант, применив двухмерную декартову систему координат.
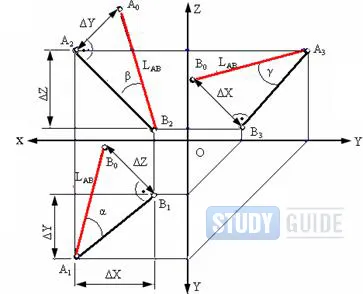
Таким образом, двумерная система координат дает координаты конечных точек отрезка. Если провести через эти точки прямую, которая должна быть перпендикулярна оси координат, то получится прямоугольный треугольник. Первая часть — это косая сторона получившегося треугольника. Катет треугольника образует отрезок, длина которого равна проекции гипотенузы на оси координат. Учитывая теорему Пифагора, мы заключаем, что Чтобы найти длину конкретного отрезка, нужно найти длину его проекции на две координатные оси.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Вычислите их, найдя разность между координатами точки на другой оси: X = X2-X1, Y = Y2-Y1.
Вычислите длину отрезка A, найдя следующий квадратный корень
A =√(X²+Y²)=√((X2-X1)²+(Y2-Y1)²).
Если координаты находятся между точками 2;4 и 4;1, то их длины равны √((4-2)²+(1-4)²) = √13≈3.61 соответственно.
Существуют три основные системы координат, используемые в геометрии, теоретической инженерии и других отраслях физики. Декартовы, полярные и сферические. В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между ними.
Вам понадобится
Рассмотрим сначала декартову систему координат. Положение точки в пространстве в этой системе координат определяется ее координатами x, y и z. Радиус-вектор строится от начальной точки к точке. Проекция этого радиус-вектора на координатные оси является координатами этой точки. Предположим, есть две точки с координатами x1, y1, z1 и x2, y2, z2 соответственно. Обозначим радиус-векторы первой и второй точек через r1 и r2 соответственно. Очевидно, что расстояние между этими двумя точками равно коэффициенту вектора r = r1-r2. Здесь (r1-r2) — это разность векторов. Координаты вектора r, очевидно, x1-x2, y1-y2 и z1-z2. Тогда мера вектора r или расстояние между двумя точками: r= sqrt((((x1-x2)^ 2)+((y1-y2)^ 2)+((z1-z2)^ 2 )).
Теперь рассмотрим полярную систему координат, в которой координаты точки задаются радиальной координатой r (радиальный вектор в плоскости XY) и угловой координатой (угол между вектором r и осью X) и координаты z, а также координаты z в декартовой системе координат. Полярные координаты точки можно преобразовать в декартовы координаты следующим образом: x = r * cos?, y = r * sin?, z = z. Расстояние между двумя точками с координатами r1, ? 1, z1 и r2, ? 2, z2 равно R = sqrt (((r1 * cos? 1- r2 * cos? 2)^ 2)+((r1 * sin ? 1-r2 * sin? 2)^ 2) + ((z1-z2)^ 2)) = sqrt ((r1 ^ 2) + (r2 ^ 2)-2r1 * r2 (cos? 1 * cos? 2+ sin? 1 * sin? 2) + ((z1-z2)^ 2))
Далее рассмотрим глобальную систему координат. В ней положение точки задается тремя координатами r ,? задаются тремя координатами r, ? и ? r — расстояние от начальной точки координат до точки ? и ? — азимутальный и зенитный углы соответственно. Угол ? Аналогичен одноименному углу в полярной системе координат. -это угол между вектором радиуса r и осью Z. 0-координаты r1, ? 1, ? 1 и r2, ? 2, ? 2 равны R = sqrt ((r1 * sin? 1 * cos? 1) — r2 * sin? 2 * cos? 2) ^ 2) + ((r1 * sin? 1 * sin? 1 — r2 * sin? 2 * sin? 2) ^ 2) + ((r1 * sin? 1 * sin? 1 — r2 * sin? 2 * sin? 2) ^ 2). cos? 1 — r2 * cos? 2)^ 2)) = ((r1 * sin? 1)^ 2) + ((r2 * sin? 2)^ 2)-2r1 * r2 * sin? 1 * sin? 2 * (cos? 1 * cos? 2 + sin? 1 * sin? 2)+ ((r1 * cos? 1 — r2 * cos? 2)^ 2)).
Если отрезок задан двумя точками в координатной плоскости, его длина может быть найдена с помощью теоремы Пифагора.

Если отрезок перпендикулярен оси, то его проекцией является точка. В декартовых системах координат одно из положений вектора имеет нулевое значение. Например, AB (0; 1) или AB (-3; 0). Так называемые единичные векторы используются для определения направления в пространстве.
Геометрия изучается в начале 7 класса, где впервые вводятся основные понятия: точки, прямые, плоскости, радиусы и отрезки. Если провести прямую линию и поставить на ней две точки, то отрезок между ними станет одним отрезком.
Равные отрезки
Равные отрезки — это отрезки одинаковой длины. Когда равные сегменты накладываются друг на друга, их края перекрываются.
Пример. Возьмите две секции CD и LM.
Расположите отрезки параллельно друг другу так, чтобы точка C находилась над точкой L, а точка D — над точкой M.
Поэтому, поскольку длины отрезков равны, CD = LM.
Сравнение отрезков
Сравнение двух отрезков означает определение того, равны ли они или один из них больше другого.
Вы можете сравнить два отрезка, проведя прямую линию из одной и той же точки к одной и той же стороне обоих отрезков. Для этого можно использовать компас.
Чтобы разместить прямой участок, совпадающий с определенным участком, сначала установите ножки компаса так, чтобы его кончик находился в конце участка. Затем, не меняя раствора компаса, переместите его так, чтобы оба конца были прямыми. .
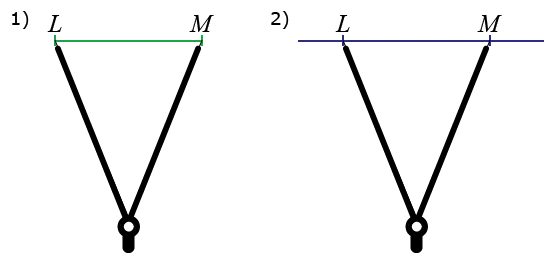
Чтобы сравнить два сегмента, можно получить один из следующих результатов. Сегменты равны, первый сегмент больше второго или первый сегмент меньше второго.
Пример. Если два линейных отрезка CA и CB добавлены из точки C, а точка A находится между C и B, то CA меньше CB (или CB больше CA).
Если точка B находится между C и A, то отрезок CA больше, чем отрезок CB (или CB меньше, чем отрезок CA):.
CA>CB или CB< CA .
Если точки A и B совпадают, то отрезки CA и CB равны.
Отрезки равны, если концы отрезков совпадают при их пересечении.
Измеряйте и сравнивайте длины отрезков: чем больше отрезок, тем больше отрезок.
Пример. Сравните длины отрезков AB и AC.
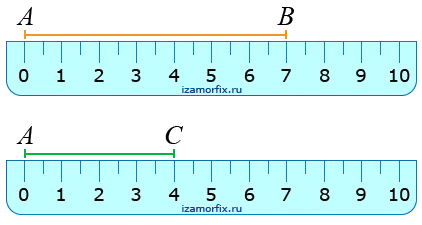
Отрезок AB больше отрезка AG, потому что
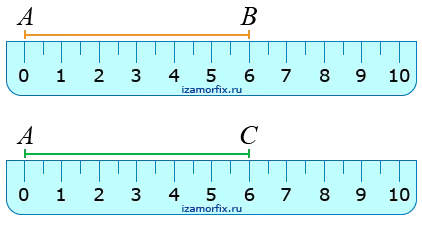
Если длины отрезков AB и AC равны, то
При измерении отрезков, если их длины равны, то отрезки равны.
Длина участка может быть определена несколькими способами. Чтобы знать, как найти длину прямой линии, достаточно иметь линейку или знать специальную формулу для ее вычисления.
Примеры решения задач с пояснениями
Дано: четыре отрезка лежат на одной прямой. AN = NB, BK = KS и AC = 5 см.
Решение: длина отрезка AC равна сумме длин составляющих его компонентов. AS = AN + NB +VC+X. Если AN = NB, BK = KS и AC = 5 см, то 2NB + 2VC = 5 (см), 2- (NB + VC) = 5 (см), NB + VC = 2,5 (см), NB + VC = NK ⇒ NK = 2,5 (см).
Дано: точки Ο, Α и Β лежат на прямой, ΟΑ = 12 см, ΟΒ = 9 см.
Поиск: расстояние между средними точками отрезков OA и OB.
Пусть M — среднее значение отрезка OA, а N — среднее значение отрезка OB.
Длина отрезка MN равна расстоянию между средними точками отрезков OA и OB, MN = MO + ON = 6 (см) + 4,5 (см) = 10,5 (см).
Если координаты находятся между точками 2;4 и 4;1, то их длины равны √((4-2)²+(1-4)²) = √13≈3.61 соответственно.
Примеры решения задач
В большинстве случаев несложно найти длину вектора с помощью координат или просто вычислить положение отрезка на плоскости. Однако, поскольку проекции очень часто используются при проверке различных физических процессов, вам необходимо уметь выполнять эти действия.
В 7 классе средней школы даны типовые вопросы для самостоятельной работы. Научившись редактировать их и находить ответы, вы сможете претендовать на знание предмета. Ниже приведены примеры различных уровней сложности.

Вот более сложные вопросы. На уровне есть две точки. Первые координаты — L (1, 5), вторые — J (2, 7). Найдите длину отрезка, соединяющего их. Чтобы понять суть проблемы, можно составить план этих двух точек и линий, которые нужно провести, соединяя их. Далее необходимо построить две вертикальные линии этих координат и пересечь их. Их пересечения записываются. Пусть будет буква Т.
На рисунке видно, что полученная фигура — не что иное, как прямоугольный треугольник. Мы видим, что секции LT и JT являются катетами. Поэтому достаточно найти их длину по модулю и применить теорему Пифагора. Таким образом, длины:| LT | = x2-x1 = 7-5 = 2, | JT | = 2 —1 = 1. Из формулы для нахождения диагоналей искомая длина равна: d=√LT2+ JT2=√22+12=√5.
Поэтому все задачи на нахождение длины или положения отрезка решаются с использованием координатного типа. Не имеет значения, какой регион исследуется. Это относится как к двумерному, так и к n-мерному пространству.
Использование онлайн-калькулятора

На практике решение задач почти всегда связано с поиском параметров в пространстве. Это особенно верно в физике, где изучаются электромагнетизм и движение. Во многих случаях точки должны быть нанесены на координатные оси, что в конечном итоге приводит к сложной геометрии. Таким образом, даже незначительные на первый взгляд ошибки могут привести к неправильным ответам.
Гораздо эффективнее использовать так называемые онлайн-компьютеры. Это обычные сайты со специальными программами для вычисления математических задач. Ими может пользоваться любой человек, имеющий доступ в Интернет и установленный интернет-браузер. Все, что нужно сделать пользователю, это ввести исходные данные в предложенную форму и нажать на интерактивную кнопку, которая часто обозначается как «Рассчитать». Приложение запускается автоматически, и ответ приходит в течение нескольких секунд. Нет необходимости беспокоиться о его точности. Кроме того, программное обеспечение использует алгоритм, основанный на математических формулах.
Среди наиболее популярных сервисов, предлагающих бесплатный доступ к своим услугам, можно назвать следующие
- ru.onlinemschool;
- ru.solverbook;
- math.semestr;
- geleot;
- mathonline.um-razum.
Эти услуги доступны на русском языке и имеют простой и понятный пользовательский интерфейс. Их услуги привлекательны не только для студентов, но и для инженеров, выполняющих сложные расчеты. В первом случае это экономит время и дает точные результаты, а во втором — очень помогает в их исследованиях. Это связано с тем, что на этих сайтах содержится весь необходимый теоретический материал, включая примеры расчетов. Кроме того, программа не только предоставляет расчеты, но и показывает пошаговые решения с пояснениями ключевых моментов.
Таким образом, учащиеся учатся самостоятельно вычислять ответы после попытки решить некоторые задачи, даже если они ничего не понимают. Векторные формулы идеально подходят для автоматических расчетов. Поэтому использование электронного калькулятора для вычисления координат вектора имеет большой полевой смысл.
Алгебраические свойства рассеяния, формулы для вычисления дисперсии дискретных случайных величин, выражения, правила и примеры расчета, онлайн калькулятор
Градиентное векторное произведение алгебраических множеств, основные свойства, формулы и условия, примеры решения задач, онлайн калькулятор
Расположите отрезки параллельно друг другу так, чтобы точка C находилась над точкой L, а точка D — над точкой M.
Геометрия 7 класс. Урок 5. Решение задач по теме «Измерение отрезков»
Основные образовательные цели курса: развить умение решать задачи и находить длину части пространства или всего пространства — научить приемам логического мышления — проверить предметные знания и изученные навыки решения задач.
-
Проверить решение дополнительной домашней задачи. (Справившийся с заданием учащийся заранее записывает решение на доске.)
Дано: AF = FB, B K = KC, AC = 5 см (рис. 1.53). Поиск: FK. решение: из условий задачи, AF = FB, BK = KS, тогда AF + FB + BK + KS = AC, 2FB + 2K = 5 см, FB + BK = 2,5 см, FB + BK = FK, тогда FK = 2,5 см. ответ: fk = 2,5 см.
(a) BC = 2,5 см (рис. 1.54). Поиск: ac. (Ответ: ac = 5 см.) б) ad = 42 см, bc = 11 см (рис. 1.55). Найдите: ab. (Ответ: ab = 20 см.) c) as = 18 дм. AB: AC = 5:4 (рис. 1.56). Поиск: ab. (Ответ: ab = 10 дм.).
Вопрос # 38 Дано, что: o, a и b — прямые линии, oa = 2 см, ob = 9 см. Поиск: расстояние между средними точками отрезков o и ob равно a) ∈ Ab, b) ∉ab. Решение: либо в середине отрезка OA, либо в середине отрезка ob. Возможны два случая (рис. 1.57): а) отрезок o ab, где mo = ao: 2 = 6 см, n = b: 2 = 4,5 см. Расстояние между средними точками отрезков OA и OB равно длине отрезка, a = Mo + on = 6 см + 4,5 см = 10,5 см. (b) Если точка O не лежит на отрезке ab, то Mo = AO: 2 = 6 см, ON = BO: 2 = 4,5 см. mn = MO -ON = 6 см -4,5 см = 1,5 см. (Ответ: a) 10,5 см — b) 1,5 см).
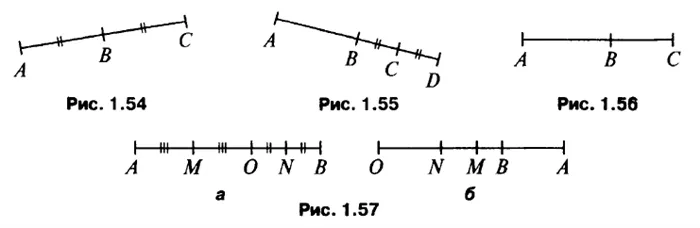
Вопрос # 40 дано: ab = 28 см, c, d ∈ Ab, m — среда ac, n — среда db. Mn = 16 см. поиск: cd. решение: ab = am + mn + nb, nb = 28 см -16 см = 12 см. так как m — среда ac, am = mc, n — среда bd, bn = nd. так как am + nb = 12 см, bn = nd, mc + dn = 12 см. Mn = MC + CD + DN = 16 см, MC + DN = 12 см, CD = MN-(MC + DN) = 16 см -12 см = 4 см (рис. 1.58). (Ответ: 4 см.)
Инструкция к вопросу: — От точек m, n, c, d отделены несколько отрезков отрезка AB. — Что вы можете сказать об этих разделах? Являются ли какие-либо из этих разделов равными? — Их длина составляет 16 см? — Какова общая длина AM и NB? Какова общая длина MC и DN? — Как найти длину отрезка компакт-диска?
Рефлексия учебной деятельности
- Как найти длину отрезка, если точка делит его на два отрезка, длины которых известны?
- Как определить, какая из трех точек лежит на прямой между двумя другими, если известны длины всех трех образовавшихся отрезков? Например, точки А, В и С лежат на одной прямой, АВ = 6 см, АС = 4 см, ВС = 10 см.
- Каким может быть взаимное расположение точек А, В и С на прямой? Как найти длину отрезка АВ в каждом случае? Например, АС = 7 см, ВС = 5 см.
- Решить задачи № 35, 36, 37, 39 из учебника.
- Решить дополнительную задачу . Длина отрезка АВ = 6 см. Внутри отрезка взята точка М. Найдите длину отрезка ВМ, если: а) АМ = 2ВМ; б) 2АМ = 3ВМ; в) АМ : ВМ = 1 : 5; г) AM : ВМ = 3 : 4; д) AM – ВМ = 2; е) 2ВМ + 3АМ = 14.
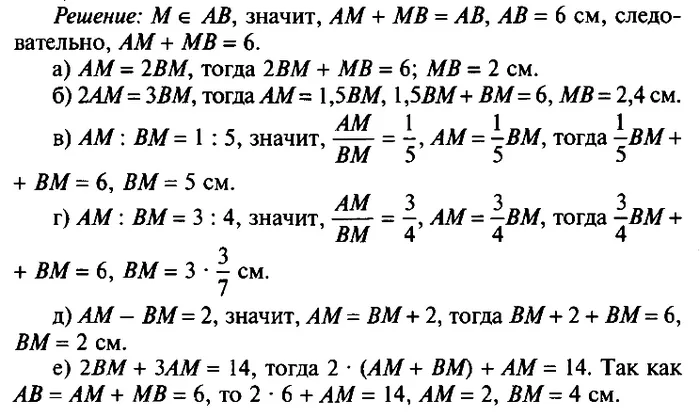
Смотреть: геометрия 7 класс. Урок 5. Решение задач и работа дома №1 «Измерение сектора». Цель — работа с основным руководством. Для руководства приведены цитаты из пособия «План курса геометрии.7 класс / Гаврилова Н.Ф.-М.: Вако.








