Мотив — это точка пересечения трех биссектрис треугольника, центр вписанной трисекции неправильной окружности, одна из замечательных точек геометрии.
Вычисление радиуса окружности, описанной около треугольника
Треугольник — это геометрическая фигура на плоскости, которая включает в себя три стороны в виде отрезков, образованных соединением трех точек, не лежащих на одной прямой.
Эта геометрическая форма обозначается символом △.
Точки A, B и C обычно обозначают вершины треугольника. Отрезки AB, BC и AC определяют стороны треугольника, которые обычно обозначаются латинской буквой. Например, AB = a, BC = b, AC = c.
注意! Если учитель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до исключения).自分で書くことができない場合は、ここで注文してください。
Внутренняя часть треугольника — это часть плоскости, ограниченная сторонами треугольника. Стороны треугольника образуют три угла при его вершинах, которые обычно обозначаются греческими буквами \(\альфа, \бета, \гамма\) и другими. По этой причине треугольник называют многоугольником с тремя углами. Символ ∠, например, также используется для обозначения углов:
Треугольники различают по величине углов или количеству равных сторон:
- остроугольный, в котором все три угла острые, то есть меньше \(90^\) ;
- тупоугольный, обладает один из углов больше \(90^\), а два остальных угла являются острыми;
- прямоугольный с одним прямым углом в \(90^\), двумя сторонами, образующими прямой угол, которые называют катетами, третьей стороной, расположенной напротив прямого угла в виде гипотенузы;
- разносторонний, со сторонами разной длины;
- равнобедренный, с двумя одинаковыми боковыми сторонами и третьей стороной в виде основания, углы при котором равны;
- равносторонний (правильный) обладает тремя сторонами с одинаковой длиной и углами, равными по \(60^\) .
Окружность — это замкнутая плоская линия, каждая точка которой равноудалена от заданной точки или центра, находящегося в той же плоскости, что и кривая.
Окружность, описанная вокруг треугольника, — это окружность, проходящая через все три вершины этого треугольника.
Радиус окружности вокруг треугольника определяется по специальным формулам, подкрепленным соответствующими доказательствами. Первая формула позволяет вычислить его по расширенной теореме синуса:
- радиус R окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла.
Формула для нахождения радиуса:
Вторая формула для нахождения радиуса окружности, описанной вокруг треугольника, записывается следующим образом:
Таким образом, чтобы определить радиус окружности, описанной вокруг треугольника, нужно произведение длин сторон этой геометрической фигуры разделить на четыре площади треугольника.
Площадь треугольника можно вычислить по формуле Герона:
В данном случае p обозначает полупериметр и определяется по формуле:
В результате преобразованная формула для определения радиуса описанной окружности вокруг треугольника будет иметь следующий вид:
Приведенные выше закономерности применимы к любому треугольнику, независимо от его формы. При расчете необходимо учитывать положение центра окружности.
Вычисление радиуса через стороны
Формулы, по которым можно определить радиус окружности, описанной вокруг треугольника, зная его стороны, были рассмотрены выше. Кроме того, при решении задач можно использовать некоторые закономерности, предусмотренные для треугольников определенного типа.
Формула для равнобедренного треугольника
Имея информацию о длинах сторон равнобедренного треугольника, мы можем определить радиус окружности, описанной вокруг этого треугольника.

где a и b — стороны треугольника.
Формула для равностороннего треугольника
Это выражение подходит для вычисления радиуса описанной окружности вокруг любого прямоугольного многоугольника. Формула имеет вид:
Здесь a — длина стороны многоугольника, а n — количество сторон многоугольника.
Частным случаем правильного многоугольника является правильный треугольник. Затем эту формулу можно применить для вычисления радиуса описанной окружности вокруг правильного треугольника.
Формула для радиуса окружности правильного треугольника:
Исключив иррациональность в знаменателе, получаем:
Обратите внимание, что для прямоугольных треугольников радиус описанной окружности в два раза больше радиуса внутренней окружности.
Формула для произвольного треугольника
Как правило, при решении задач по геометрии необходимо вычислить радиус контура вокруг любого заданного треугольника. В этом случае имеет смысл использовать следующую формулу
Применяется следующее уравнение
где α, β и γ — длины сторон треугольника, \ (\ альфа, \ бета, \ гамма \) — углы напротив этих сторон, а S — площадь треугольника.
Формула для прямоугольного треугольника
Радиус окружности, описанной вокруг прямоугольного треугольника, можно найти с помощью следующего уравнения.

Так, для прямоугольного треугольника радиус описанной вокруг него окружности равен половине гипотенузы. Как правило, он обозначается символом «c». То есть AB = c. Таким образом, уравнение становится.
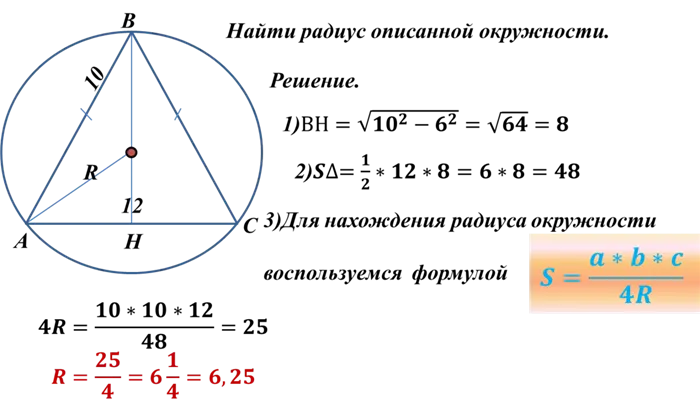
Примеры решения задач
Стороны треугольника равны 4, 6 и 9 см. Вам нужно определить радиус окружности, нарисованной вокруг треугольника.
Первое, что вам нужно сделать, это вычислить площадь этого треугольника. Если вам известны длины сторон, вы можете определить их по формуле Герона.
Затем найдите радиус окружности.
ОТВЕТ: радиус окружности равен 5,65 см.
Известно, что катеты прямоугольного треугольника равны 6 см и 8 см. Вам нужно вычислить радиус окружности, нарисованной вокруг этого треугольника.
Используйте теорему Пифагора для определения косых сторон этого треугольника.
Известно, что радиус окружности, проведенной вокруг правильного треугольника, равен половине гипотенузы. Поэтому.
ОТВЕТ: радиус окружности равен 5 см.
Стороны равны \(AB = 4 \ sqrt \)см, \(\ AC = 7 см \)и \(\ угол A = 45 ^. \Определите радиус окружности вокруг треугольника ABC, который равен Ј(Ј).
Радиус окружности, проведенной вокруг треугольника, равен произведению его площади стороны и 4.
Используйте теорему косинусов для вычисления стороны BC.
Затем можно определить площадь треугольника ABC:.
\ S_ = \ frac \ cdot AB \ cdot AC \ cdot \ sin\ угол A = 14 \ см ^ 2 \)
Если вы знаете площадь, вы можете легко вычислить радиус круга.
ОТВЕТ: радиус окружности равен ⌘ (⌘ frac> 2 см. ⌘)
Треугольник ABC задан стороной AB = 3 см, ⌘ (⌘ AC = \ sqrt cm \). Определите угол этой геометрической фигуры. Радиус окружности равен ⌘ (R = \ sqrt см \).
Согласно формуле, радиус окружности равен отношению удвоенного полутона угла, противолежащего стороне треугольника.
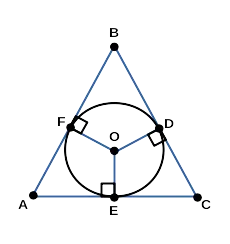
На следующей диаграмме изображена окружность, вписанная в треугольник, и треугольник, очерченный вокруг окружности.
Окружность, описанная около треугольника
Определение 2. Периметр треугольника — это окружность, проходящая через все три вершины треугольника (рис. 5). В этом случае треугольник называется вписанным или обведенным.
Свойства описанной около треугольника окружности. Теорема синусов
Уравнение (теорема синуса) применимо к каждому треугольнику.
где α, β и γ — стороны треугольника, Α, Β и Γ — углы треугольника, а R — радиус окружности.
Для каждого треугольника применимы следующие уравнения
где A, B и C — углы треугольника, S — площадь треугольника, а R — радиус контура.
Для каждого треугольника применимы следующие уравнения
где a, b, c — стороны треугольника, S — площадь треугольника, R — радиус контура.
| Серединные перпендикуляры к сторонам треугольника |
 |
Все перпендикуляры к сторонам любого треугольника пересекаются в одной точке.
Вокруг любого треугольника можно описать окружность. Центр окружности, проведенной вокруг треугольника, — это точка пересечения всех перпендикулярных линий, проведенных на сторонах треугольника.
Центр окружности треугольника с острым углом находится внутри треугольника.
Центр окружности, проведенной вокруг прямоугольного треугольника, является серединой наклонной стороны.
Центр окружности, проведенной вокруг тупоугольного треугольника, находится вне треугольника.
Уравнение (теорема синуса) применимо к каждому треугольнику.
где α, β и γ — стороны треугольника, Α, Β и Γ — углы треугольника, а R — радиус окружности.
Для каждого треугольника применимы следующие уравнения
где A, B и C — углы треугольника, S — площадь треугольника, а R — радиус контура.
Для каждого треугольника применимы следующие уравнения
где a, b, c — стороны треугольника, S — площадь треугольника, R — радиус контура.
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3. Все перпендикуляры к сторонам любого треугольника имеют одну общую черту.
Доказательство Рассмотрим две середины сторон AC и AB треугольника ABC и обозначим их пересечение через O (рис. 6).
Поскольку O лежит в центре перпендикулярной линии AC, согласно Теореме 1, имеет место следующее уравнение.
Так как точка O находится в центре перпендикуляра к отрезку AB, то, согласно теореме 1, имеет место следующее уравнение
Следовательно, уравнение верно.
Поэтому, согласно Теореме 2, делаем вывод, что точка O лежит на серединном перпендикуляре к отрезку BC. Следовательно, все три перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Результат. Можно заключить любой треугольник. Центр периметра треугольника — это точка, в которой все медианы проходят через все перпендикулярные линии на сторонах треугольника.
Доказательства. Рассмотрим точку O, в которой все средние точки пересекаются по всем перпендикулярным линиям сторон ABC (рис. 6).
Доказательство Теоремы 3 показывает уравнение.
Видно, что окружность с центром O и радиусами OA, OB и OC проходит через все три вершины ABC. Это нужно было доказать.
Теорема 4 (теорема синуса). Для каждого треугольника (рис. 7)
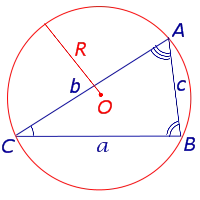
Доказательство Сначала докажем, что длина струны вписанной в окружность радиуса R величиной φ вычисляется по следующему уравнению.
Сначала рассмотрим случай, когда одна из сторон окружного угла является диаметром круга (рис. 8).
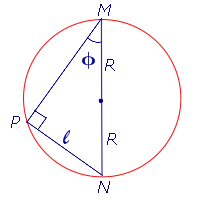
Поскольку все углы окружности на одной дуге равны, для любого угла окружности всегда существует угол окружности, одна из сторон которого является диаметром окружности.
В прямоугольном треугольнике центр окружности находится в середине гипотенузы.
Нахождение радиуса описанной вокруг треугольника окружности
В этом материале мы рассмотрим формулы, которые можно использовать для вычисления радиуса окружности, описанной вокруг любого (произвольного) прямоугольного или равностороннего треугольника. Также будут рассмотрены примеры решения проблем для закрепления представленного теоретического материала.
Произвольный треугольник
Радиус окружности, описанной вокруг треугольника, вычисляется по формуле
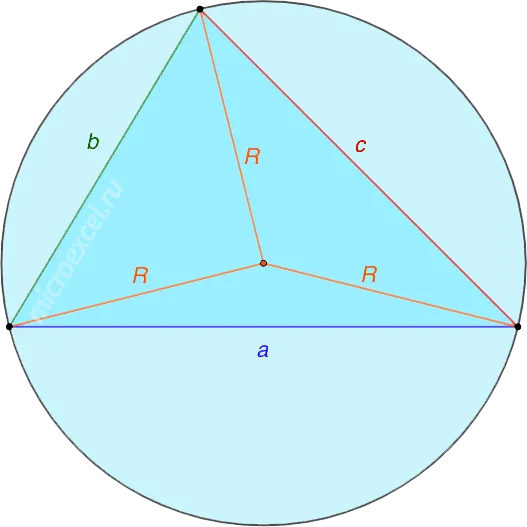
где α, β и γ — стороны треугольника, а S — его площадь.
Прямоугольный треугольник
Радиус окружности, описанной вокруг прямоугольного треугольника, равен половине косой стороны или высоте, выходящей за пределы косой стороны.
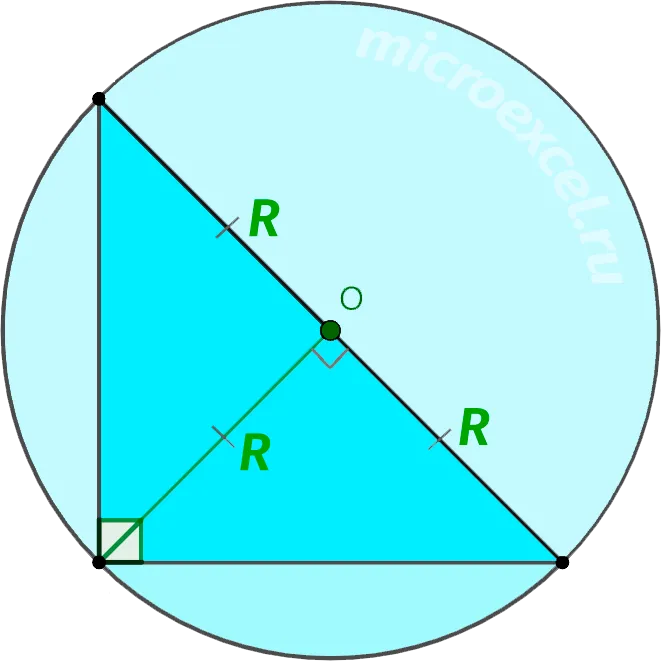
Равносторонний треугольник
Радиус окружности, описанной вокруг прямоугольного треугольника, вычисляется по формуле
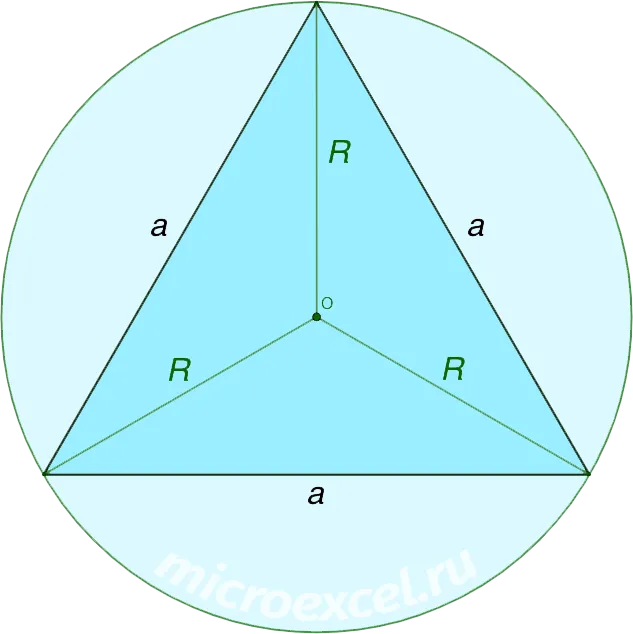
где a — сторона треугольника.
Примеры задач
Задача 1 Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус окружности вокруг него.
Решение Сначала нужно найти площадь треугольника. Если известны длины всех сторон, можно применить формулу Герона.
![]()
Теперь вы можете использовать первую формулу выше для расчета радиуса окружности.
Задача 2 У треугольника две стороны с тремя известными сторонами 6 см и 8 см. Найдите радиус описанной вокруг них окружности.
РешениеТреугольник с одной стороной 6 см и одной стороной 8 см является только прямоугольником, а сторона, известная из условия задачи, является катетом. Поэтому теорема Пифагора может быть использована для нахождения косых сторон на диаграмме.
Как известно, радиус окружности, проведенной вокруг правильного треугольника, равен половине косой стороны, поэтому R = 10:2 = 5.
Треугольник равен, если угол между одной стороной и двумя смежными углами одного из окружающих треугольников равен стороне и двум смежным углам другого окружающего треугольника.
Как найти радиус описанной окружности треугольника
Если все стороны треугольника совпадают с контуром, то окружность называется вписанной в треугольник, а треугольник — контуром вокруг окружности.
Теорема. Окружность можно вписать в любой треугольник и только в один из них.
Окружность, вписанная в треугольник, имеет биссектрисы в точках пересечения.
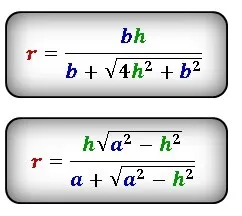
Описанная окружность
Если все вершины многоугольника лежат на окружности, то окружность называется кругом, а треугольник вписан в окружность.
Теорема. Вокруг любого треугольника можно нарисовать окружность, причем только одну.
Центр описанной окружности вокруг треугольника лежит в точке пересечения средних точек перпендикулярных прямых.
Окружность прямоугольного треугольника лежит в центре гипотенузы, а его радиус равен половине гипотенузы.
Признаки равенства
Доказательство 1. Две стороны и угол между ними.
Если угол между двумя сторонами и одним контуром равен углу между двумя сторонами и другим контуром между ними, то они конгруэнтны.
Доказательство 2. Одна сторона и два смежных угла.
Треугольник равен, если угол между одной стороной и двумя смежными углами одного из окружающих треугольников равен стороне и двум смежным углам другого окружающего треугольника.
Доказательство 3. в соответствии с тремя сторонами.
Если три стороны треугольника равны трем сторонам другого треугольника.
Как известно, любой треугольник можно описать вокруг окружности, поэтому можно сказать, что вокруг окружности можно описать следующие типы треугольников
- Разносторонний треугольник
- Равносторонний / правильный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равнобедренный прямоугольный треугольник
- Прямоугольный треугольник, описанный около окружности
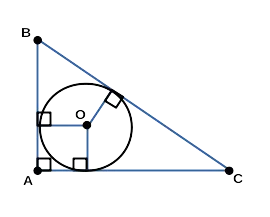
Характерные признаки: один из углов правильный, длины сторон можно найти по теореме Пифагора, а сумма острых углов равна 90 градусам.
Основные типы:.
Характерные точки: два угла равны, две стороны равны и третий угол можно найти, зная два других.
Основные типы:.
Основные типы:.
Термины
Точка касания — это точка, в которой вписанная окружность является касательной к треугольнику. Это общая точка между треугольником и треугольником по обе стороны от него.
Мотив — это точка пересечения трех биссектрис треугольника, центр вписанной трисекции неправильной окружности, одна из замечательных точек геометрии.
Касательные — это стороны треугольника и общие точки в клетке, т.е. точки касания.
Орто — это точка пересечения высот треугольника.
Ось симметрии — это линия, делящая треугольник на равные половины.
Точка касания является точкой пересечения медианного класса, высоты, деления и средней точки.
Касательная — это отрезок, который начинается в одной из вершин треугольника и заканчивается в точке касания.








