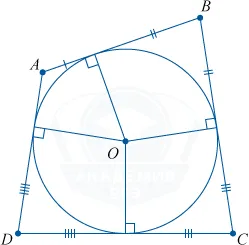
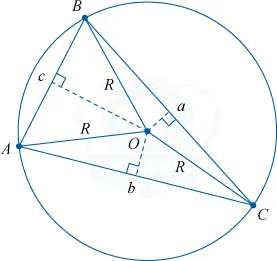
Вокруг любого треугольника можно описать окружность и описать только один цикл. Центр такого цикла находится в точке пересечения средних вертикалей треугольников.
Окружность и круг
Во-первых, поймите разницу между циклом и периметром. Чтобы определить разницу, достаточно рассмотреть, что представляют собой эти два элемента. Это бесконечное количество точек на уровне на равных расстояниях от одной центральной точки. Однако круг состоит из внутренностей, в то время как окружность не состоит из внутренностей. Установлено, что круг является одновременно и окружностью, которая его очерчивает (O-Circus), и бесконечным числом точек круга.
Цикл — это серия точек, расположенных на фиксированном расстоянии от центра, представленного одной точкой.
Для каждой точки L окружности выполняется равенство OL = r. (Длина отрезка OL равна радиусу окружности).
Отрезок, соединяющий две точки окружности, является ее струной.
Нить, проходящая непосредственно через центр круга, является диаметром круга (d). Диаметр можно рассчитать по следующему виду: d = 2R
Окружность круга вычисляется по типу c = 2 \ pi r
Площадь круга: s = \ pi r^
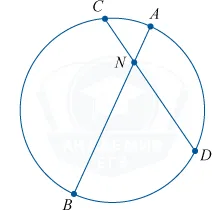
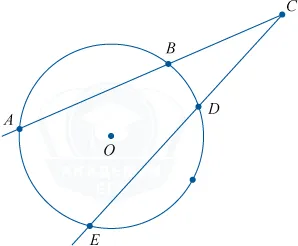
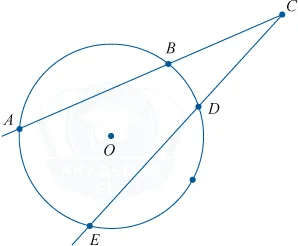
Дуга окружности — это часть окружности между двумя ее точками. Эти две точки определяют два лука окружности. Струна CD сжимает два смычка CMD и CLD. Одна и та же струна натягивает один и тот же лук.
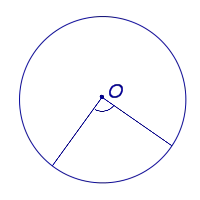
Центральный угол — это угол между двумя лучами.
Длина дуги может быть найдена с помощью следующих типов
Диаметр, перпендикулярный струне, разделяет струну и узкую дугу посередине.
Если прямые AB и CD окружности имеют общую точку n, то прямые равны между собой.
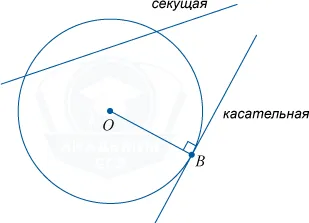
Касательная к окружности
Касательная к окружности — это прямая, имеющая общую точку с окружностью.
Если прямой объект имеет две общие точки, он называется квадратичным.
Когда балка проектируется с помощью касательной линии, она перпендикулярна окружности.
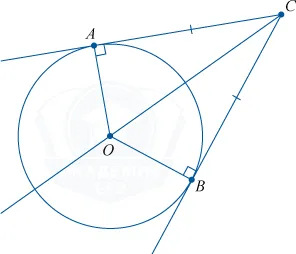
Проведите две касательные из этой точки к окружности. Отрезки касательных совпадают друг с другом, а центр окружности находится в дихотомической форме угла при вершине в этой точке.
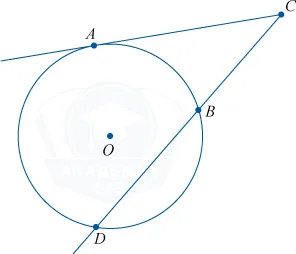
Теперь постройте касательную и вторичную из нашей точки к окружности. Находим, что квадрат длины касательного сечения равен произведению всего вторичного сечения на его внешнюю часть.
Мы можем заключить, что. Произведение внешней части первой вторичной части равно произведению целой части второй вторичной части на внешнюю часть.
Углы в окружности
Градус центрального угла и дуги, на которой он базируется, равны.
Регистрационный угол — это угол, вершина которого находится на окружности, а сторона содержит строку.
Она равна половине этого лука и поэтому может быть вычислена путем нахождения меры лука.
Угол, основанный на диаметре и угле регистрации, является прямым углом.
\ угол cbd = \ угол ced = \ угол cad = 90^
Углы регистрации, основанные на одном и том же смычке, идентичны.
\ угол adb = \ угол ab = \ угол afb
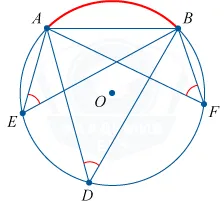
Регистрационные углы, основанные на одной и той же струне, одинаковы или в сумме равны 180^.
\ угол adb + \ угол akb = 180^.
\ угол adb = \ угол ab = \ угол afb
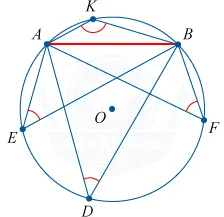
Тот же круг имеет верхнюю часть треугольника с тем же углом и определенным основанием.
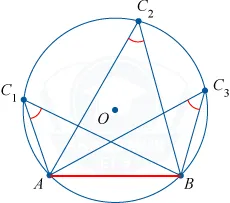
Угол между верхней окружностью и двумя струнами равен половине суммы углов окружностей, окружающих данный угол и вертикальный угол.
\ угол dmc = \ угол adm + \ угол dam = \ frac \ слева (\ чашка dmc + \ чашка alb \ справа)
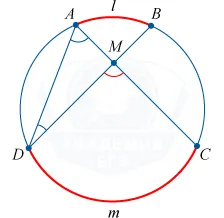
Угол с внешней вершиной окружности между двумя частями равен половине разницы между значениями угла окружности, заключенной внутри угла.
Угол M = \ Угол CBD — \ Угол Acb = \ frac \ слева (ߋ cup dmc- \ cup alb \ справа)
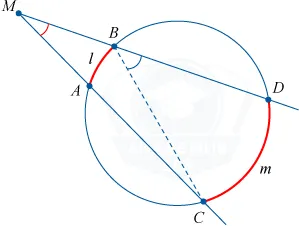
На этой диаграмме изображена пара дуг dž (dž displaystyle ab dž) и два центральных угла. Самый большой лук соответствует самому большому углу, но больше, чем 섹 (섹 displaystyle 180<>^ ⌘ circ \) и наименьшая дуга соответствует меньшему углу.
Теоремы о вписанных и центральных углах
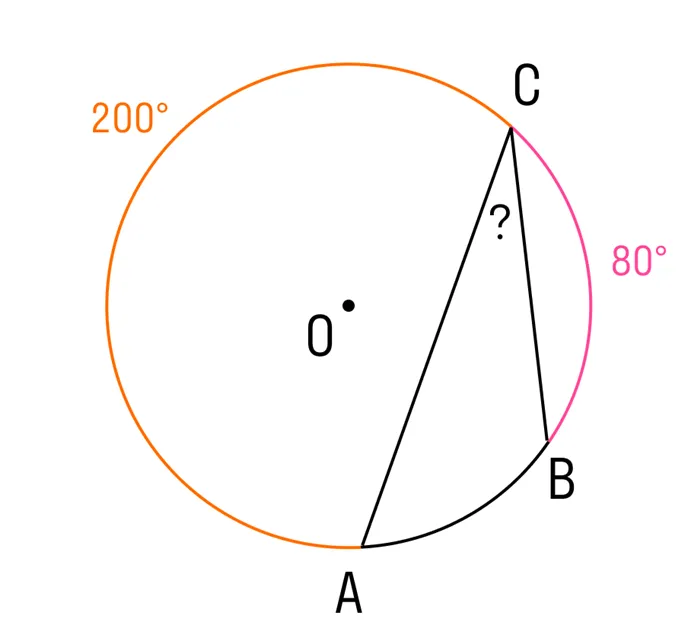
Стоимость зарегистрированного угла равна половине стоимости центрального угла на той же дуге.
Центр под прямоугольного треугольника является центром периметра периметра.
Стоимость зарегистрированного угла равна половине стоимости центрального угла на той же дуге.
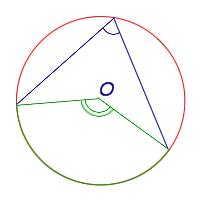
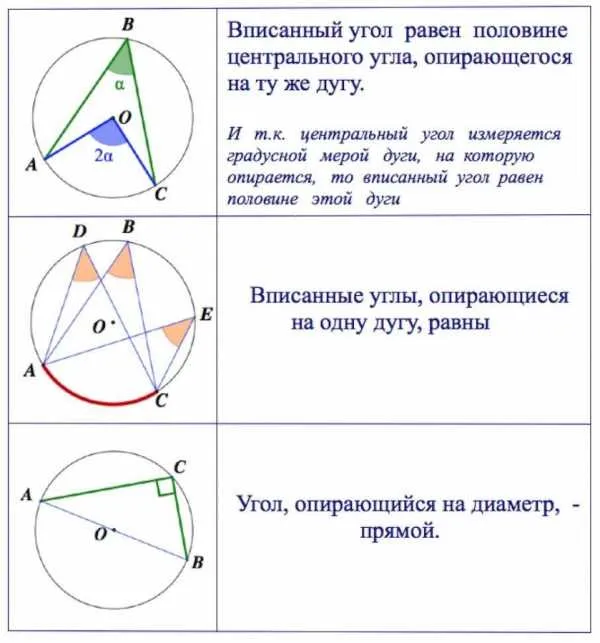
Углы регистрации, основанные на одной и той же дуге, равны.

Регистрационные углы, перпендикулярные одной и той же струне, равны, если вершины находятся по одну сторону от этой струны.
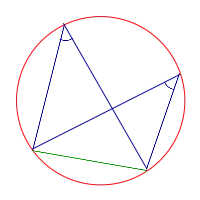
Два регистрационных угла, перпендикулярных одной и той же струне, складываются в 180°, если вершины находятся на противоположных сторонах этой струны.
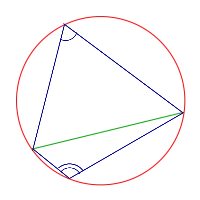
Регистрационные углы перпендикулярны только в том случае, если они лежат на диаметре
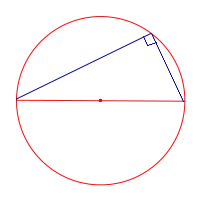
Центр под прямоугольного треугольника является центром периметра периметра.

Теоремы об углах, образованных хордами, касательными и секущими
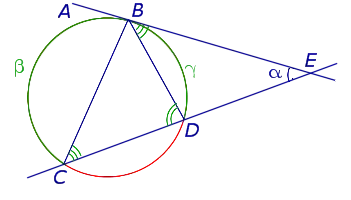
Цена угла, образованного пересекающимися струнами, равна половине суммы арок, заключенных между их сторонами.
Угол, образованный пересекающимися отрезками на внешней стороне диска, равен половине суммы углов дуг, примыкающих к его сторонам.
Угол, образованный касательной и струной, проходящей через точку касания, равен половине цены дуги, заключенной между ее сторонами.
Угол, образованный касательной и вторичным углом, равен половине разности размеров дуги, заключенной между его сторонами.
Угол, образованный двумя касательными к окружности, равен половине разности размеров дуги, заключенной между сторонами.
Цена угла, образованного пересекающимися струнами, равна половине суммы арок, заключенных между их сторонами.
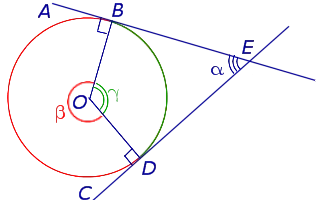
Угол, образованный пересекающимися отрезками на внешней стороне диска, равен половине суммы углов дуг, примыкающих к его сторонам.
Угол, образованный касательной и струной, проходящей через точку касания, равен половине цены дуги, заключенной между ее сторонами.

Угол, образованный касательной и вторичным углом, равен половине разности размеров дуги, заключенной между его сторонами.
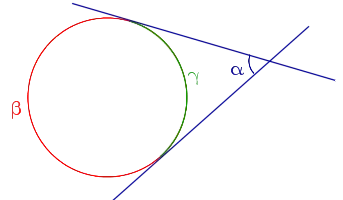
Угол, образованный двумя касательными к окружности, равен половине разности размеров дуги, заключенной между сторонами.
Доказательства теорем об углах, связанных с окружностью
Теорема 1. Размер зарегистрированного угла равен половине размера центрального угла, расположенного на том же луке.
Доказательство Сначала рассмотрим зарегистрированный угол ABC, сторона BC которого является диаметром окружности, а центральный угол AOC (рис. 5).
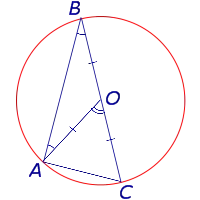
Таким образом, Теорема 1 доказывается, если одна сторона в клетке проходит через центр цикла.
Теперь рассмотрим случай, когда центр окружности лежит внутри зарегистрированного угла (рис. 6).
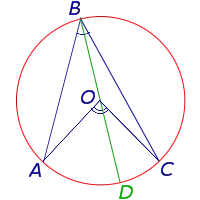
Применяется следующее
Теорема 1 доказана.
Еще неизвестно, что центр цикла лежит вне угла регистрации (рис. 7).
Применяется следующее
Доказательство Теоремы 1 завершено.
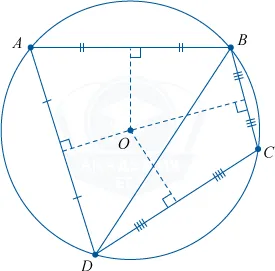
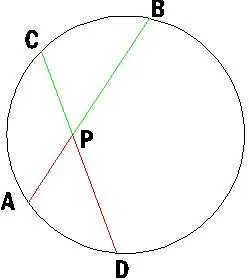
Теорема 2. Цена угла, образованного пересекающимися струнами, равна половине суммы дуг между их сторонами.
Доказательства Рассмотрим рисунок 8.
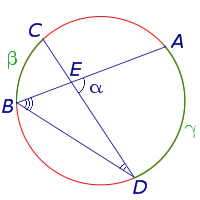
Нас интересует величина угла AED, образованного нитями AB и CD, пересекающимися в точке E. Поскольку угол AED является внешним углом треугольника BED, а углы CDB и ABD — штампованные углы, следует, что
Доказательство.
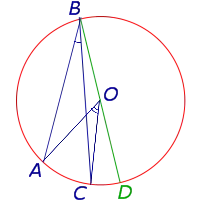
Теорема 3. Угол, образованный сторонами пересекающихся сторон вне круга, равен половине разности размеров дуги, заключенной между сторонами угла.
Доказательства. Рассмотрим рисунок 9.
Нас интересует угол BED, образованный пересечением AB и CD в точке E. Поскольку ADC — внешний угол треугольника ADE, а углы ADC, DCB и DAB — углы штампованные, получаем следующее уравнение.
Доказательство.
Теорема 4. Угол, образованный касательной, нитью касания и нитью, проходящей через точку касания, равен половине величины дуги, ограниченной его сторонами.
Доказательства. Рассмотрим рисунок 10.
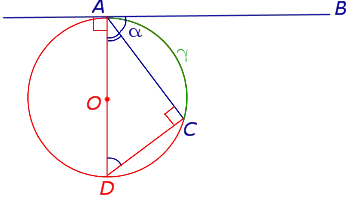
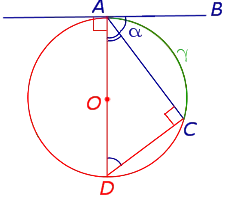
Нас интересует угол BAC, образованный касательной AB и струной AC. Углы DAB и DCA являются прямыми углами, так как AD — это диаметр, проходящий через точку контакта, а угол ACD — это угол, вырезанный на основе диаметра. Поэтому применяется следующее уравнение
Дуга окружности — это часть окружности между двумя ее точками. Эти две точки определяют два лука окружности. Струна CD сжимает два смычка CMD и CLD. Одна и та же струна натягивает один и тот же лук.
Центральный угол и вписанный угол
Окружность — это замкнутая линия, все точки которой равноудалены от центра.
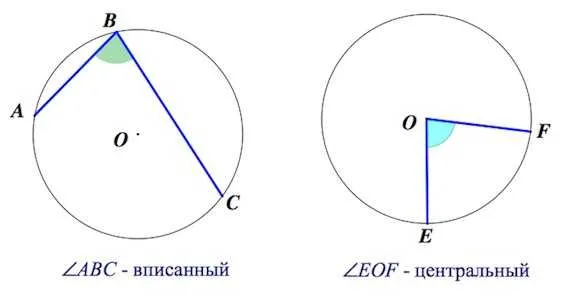
Установка центрального угла:.
Центральный угол — это угол, при котором вершина лежит в центре окружности. Центральный угол равен углу дуги, на которой он расположен.
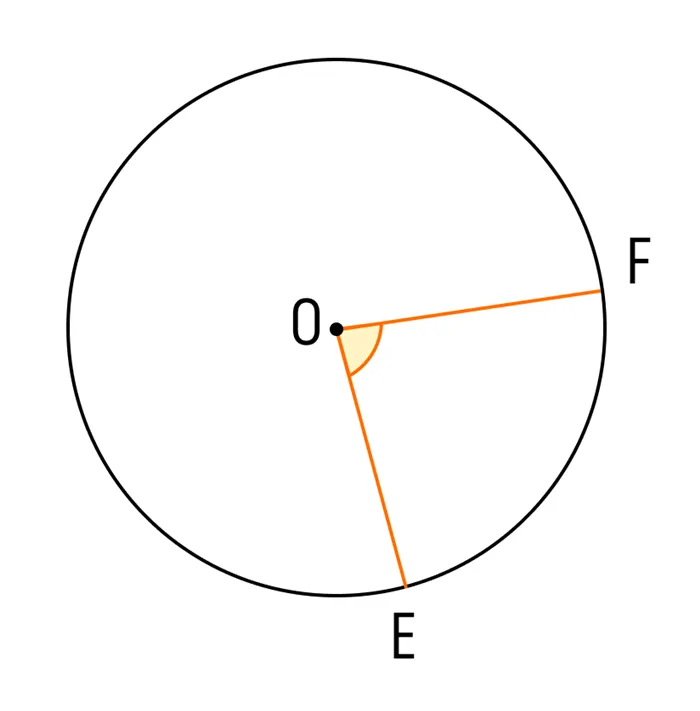
Изображение: центральный угол окружности EOF и дуга, на которой находится EF.
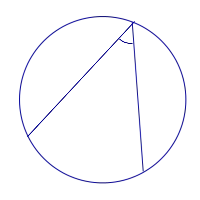
Установите угол записи.
Выгравированный угол — это угол, под которым вершина является круговой.
Выгравированный угол равен половине дуги, на которой он расположен.
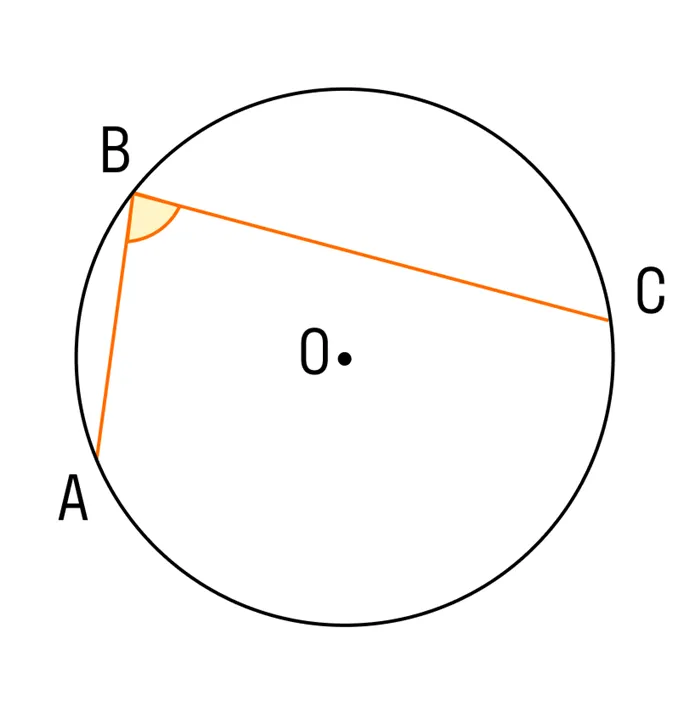
Угол ABC, выгравированный на окружности, и дуга, на которую наклонена AC
Свойства центральных и вписанных углов
Ракурсы на первый взгляд просты. Свойства центрального угла и гравированного угла помогают быстро и легко решить проблему.
AOC является центром, а ABC зарегистрирован. Поскольку оба угла опираются на AC, центральный угол равен AC, а угол ABC равен половине угла AOC.
ㄥADC=ㄥABC=. AEC, так как все три угла, вписанные в окружность, опираются на одну и ту же дугу AC.
ㄥACB основывается на диаметре и дуге AB — диаметр делит круг на две равные части. Поэтому дуга AB = 180ㄥΕ4D, ㄥCAB равна половине дуги, на которой она расположена, поэтому ㄥCAB =90ㄥΕ4D.
Если есть гравированный угол, то есть и гравированный угол. Выгравированный угол — это угол, образованный двумя касательными к окружности. Такие как:.
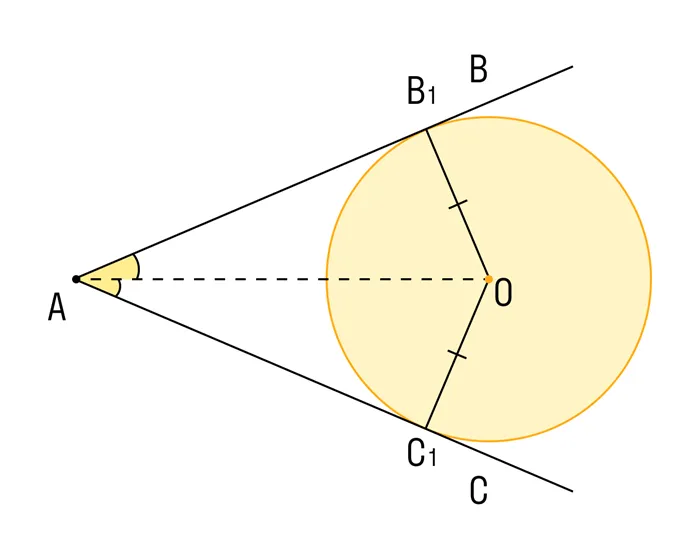
На диаграмме: ㄥCAB образована двумя касательными к окружности. AO — биссектриса ㄥCAB, поэтому центр окружности находится на биссектрисе окружающей окружности.
Для решения этих задач недостаточно знать, какие углы являются вписанными, а какие — очерченными. Вам необходимо знать, что такое строка и каковы ее свойства.
Нужно упорядочить свои знания перед экзаменом? Записывайтесь на занятия ЕГЭ по математике в Skysmart!
Струна — это отрезок, соединяющий две точки окружности.
AB * AC = AE*AD Докажите, что стороны угла, вписанного в окружность, — струны.
ㄥBAC=ㄥCAB, потому что он находится на строке BC.
Примеры решения задач
Как и все остальное, центрированные, гравированные и обведенные углы требуют практики для решения. Изучите примеры решения и потренируйтесь самостоятельно.
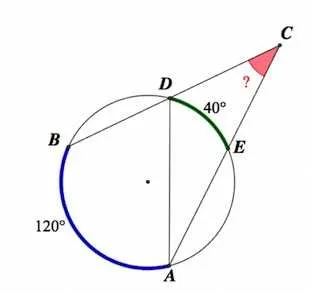
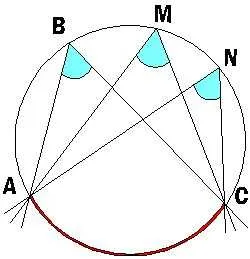
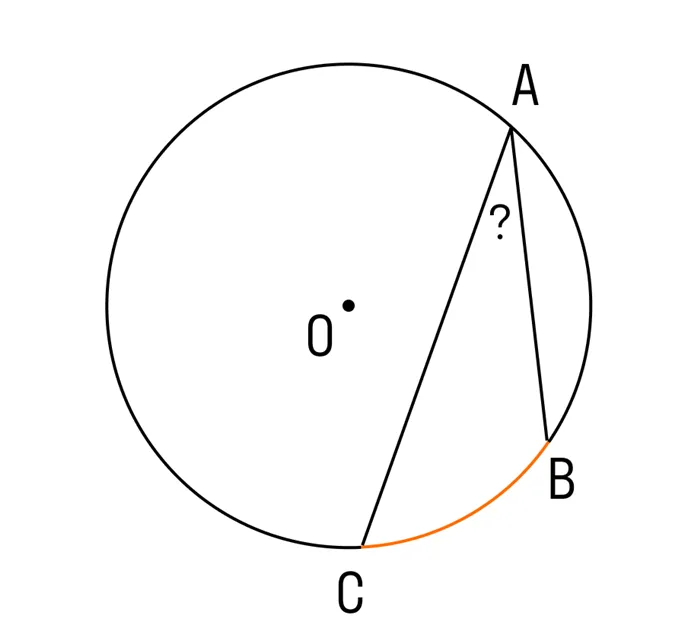
Вопрос 1. Дан цикл, ARC AC = 200°, ARC BC = 80°. Найдите угол, зарегистрированный в дуге AB. ㄥacb =?
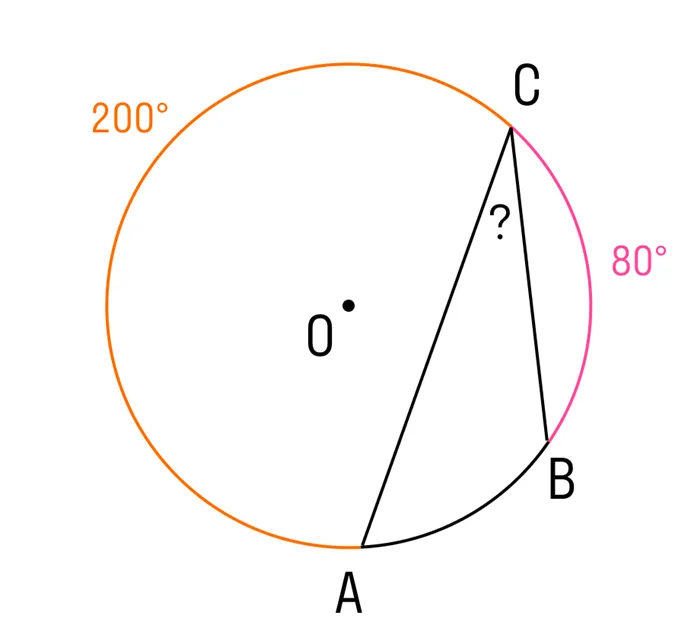
Решение: 360°-AC -CB = 360°-200°-80°= 80°Теорема: Зарегистрированный угол равен одной дуге ½. acb =½ab= 40°.
Задача 2. Учитывая цикл, AOC = 140°, найдите значение угла регистрации.
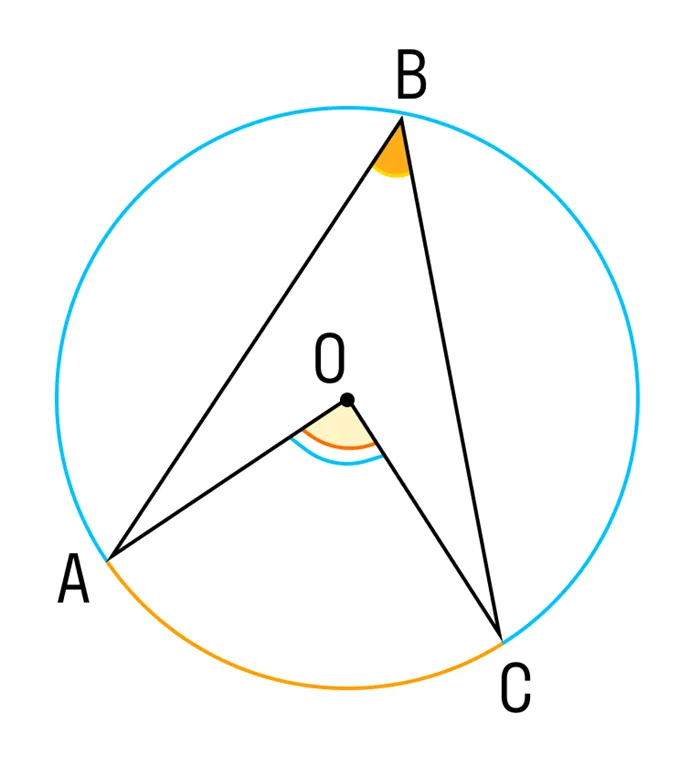
Мы уже практиковались и знаем, как найти записанный угол. На диаграмме окружности мы знаем, что для центрального угла и дуги AC = 140°, угол регистрации равен половине центрального угла.
Вопрос 3: Какой угол записан на окружности на основе лука?
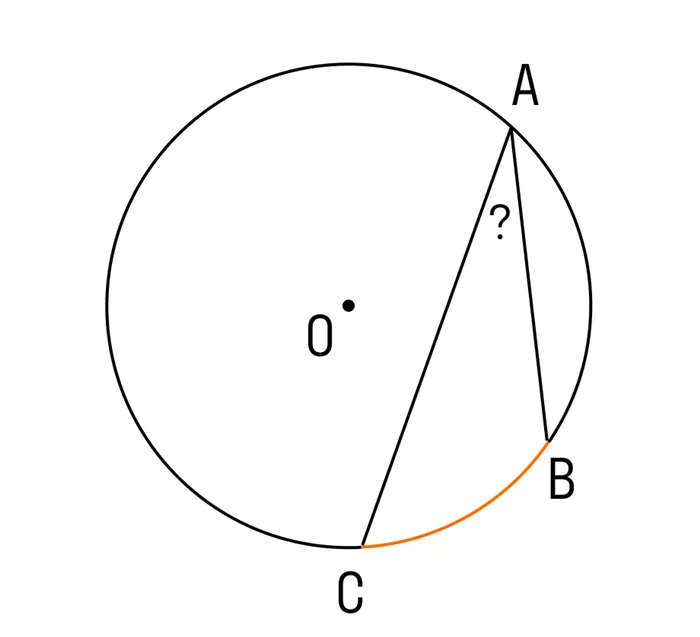
CB = 360° = 72°, так как угол регистрации равен половине носового угла, cb = cb = 72° / 2 = 36° Cab =½.
Теорема 5. Угол, образованный касательной и квадратиком квадрата, равен половине разности дуг между сторонами угла.
Вписанный угол вдвое меньше центрального — доказательство
Есть великое событие:
Цена зарегистрированного угла составляет половину цены соответствующего центрального угла.
Посмотрите на рисунок, чтобы увидеть, как выглядит это утверждение. Соответствующим» центральным углом считается такой, у которого край совпадает с краем угла регистрации, а вершина находится в центре.
Соответствующий центральный угол также должен «отображать» тот же код (⌘ displaystyle ac \), что и регистрационный угол.
Почему? Почему зарегистрированные углы составляют половину от центральных углов?
Сначала рассмотрим простой случай.
Случай 1. Хорда проходит через центр окружности
Предположим, что одна из струн проходит через центр. Иногда это случается, не так ли?
Что не так? \Согласитесь с \ (⌘ displaystyle \ delta aob \). Это потому, что \(\ displaystyle ao \) и \(\ displaystyle ob \) являются световыми лучами. поэтому \ (⌘ displaystyle \ угол a = \ угол b \) (мы называем это ⌘ displaystyle \ альфа \).
Теперь давайте рассмотрим 팀 (팀 displaystyle 팀 angle aoc 팀). Это внешний угол ɑ (ɑ displaystyle \ delta aob \)!
Мы можем заключить, что. Произведение внешней части первой вторичной части равно произведению целой части второй вторичной части на внешнюю часть.
Примеры решения задач
Существуют определенные циклы, в которых дуга символизации AC равна ⌘ (⌘ DisplayStyle 200<>^\\\\ circ \), bc bow is \(\ DisplayStyle 80).<>^\\\\ круг \). Вычислите значение зарегистрированного угла на дуге ab.
Окружности — это ዄ (ዄ displaystyle 360.).<>^\ circ \). Для того чтобы найти лук аб, вам нужно.
\ \ \ displaystyle 360.<>^\ circ -ac -cb = 360-200-80 = 80 \)
Согласно теореме о регистрационном угле, его величина равна половине лука, на который он опирается. Итак.
\ (ac =½ab= \ displaystyle 40)<>^\ круг \)
Ответ: ac Угол IS \ (⌘ DisplayStyle 40<>^\ круг \)
Дана окружность. Угол AC IS ⌘ (⌘ Displaystyle 140.<>^\ circ \). Необходимо определить значение угла регистрации.
На этой диаграмме показано, что окружность имеет центральный угол и дугу AC. Это ⌘ (⌘ displaystyle 140).<>^\ circ \). Из теоремы к зарегистрированному и центральному углам, зарегистрированный угол равен половине центрального угла. Тип может быть записан:.
\ (ABC =½AC= 140/2 = \ DisplayStyle 70)<>^\ круг \)
ОТВЕТ: угол ABC равен ⌘ (⌘ DisplayStyle 70.<>^\ circ \).
Вам необходимо рассчитать значение угла, записанного на носовом круге. Лук составляет 1/5 цикла.
Известно, что окружность ⌘ (⌘ displaystyle 360)<>(^\ circ \). Итак.
\ (cb =⅕\ от \ 360 = \ displaystyle 72)<>^\ круг \)
Согласно теореме о зарегистрированном угле, он равен половине лежащей в основе дуги.
Здесь мы имеем еще одно распространенное выражение: «струна сжимает лук». Здесь, например, строка \(⌘ displaystyle ab \) ограничивает смычок \(⌘ displaystyle ab \).
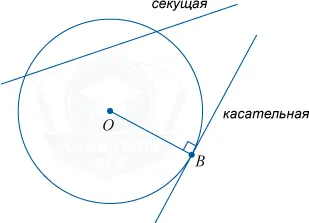
Касательная к окружности
Касательная к окружности — это прямая, имеющая общую точку с окружностью. Если линия имеет две общие точки, она называется вторичной.
Когда балка проектируется с помощью касательной линии, она перпендикулярна окружности.
Проведите две касательные из этой точки к окружности. Отрезки касательных совпадают друг с другом, а центр окружности находится в дихотомической форме угла при вершине в этой точке.
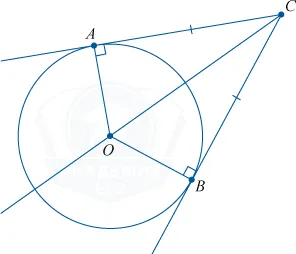
Теперь постройте касательную и вторичную из нашей точки к окружности. Находим, что квадрат длины касательного сечения равен произведению всего вторичного сечения на его внешнюю часть.
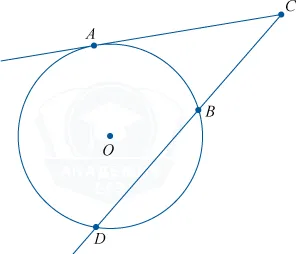
Мы можем заключить, что. Произведение внешней части первой вторичной части равно произведению целой части второй вторичной части на внешнюю часть.
Углы в окружности
Градус центрального угла и дуги, на которой он базируется, равны.
Регистрационный угол — это угол, вершина которого находится на окружности, а сторона содержит строку.
Она равна половине этого лука и поэтому может быть вычислена путем нахождения меры лука.
Угол, основанный на диаметре и угле регистрации, является прямым углом.
Угол cbd = угол ced = угол cad = 90^.
Углы регистрации, основанные на одном и том же смычке, идентичны.
Угол ADB = Угол AEB = Угол AFB
Регистрационные углы, основанные на одной и той же струне, одинаковы или в сумме равны 180^.
Угол ADB + Угол AKB = 180^.
Угол ADB = Угол AEB = Угол AFB
Тот же круг имеет верхнюю часть треугольника с тем же углом и определенным основанием.
Угол между верхней окружностью и двумя струнами равен половине суммы углов окружностей, окружающих данный угол и вертикальный угол.
Угол dmc = угол ADM + угол dam = frac left (чашка DMC + чашка альбита)
Угол с внешней вершиной окружности между двумя частями равен половине разницы между значениями угла окружности, заключенной внутри угла.
Угол M = угол CBD — Угол ACB = FRAC LEFT (CUP DMC -CUP ALBIGHT)
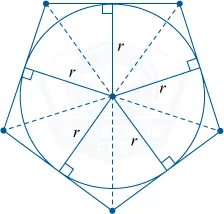
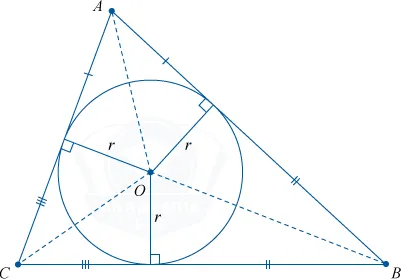
Вписанная окружность
Зарегистрированный цикл — это конкретный круг на стороне многоугольника.
Его центр находится в точке пересечения угловых дихотомий многоугольников.
Не все многоугольники могут быть зарегистрированы как круг.
Площадь многоугольника с циклом регистрации задается типом
p — половина границы многоугольника, и
R — радиус в камере.
Предполагается, что радиусы в ячейках равны.
Сумма противоположных длин такая же, как если бы окружность была зарегистрирована на выпуклом четырехугольнике. И наоборот, если сумма противоположных длин одинакова, то круг регистрируется в выпуклом четырехугольнике.
Можно зарегистрировать круг в любом из треугольников. Только один. В точке, где найден внутренний угол, находится центр в клетке.
Академические радиусы рассчитываются с использованием следующих типов.








